9-量子團簇態信道的非對稱雙向量子信息傳輸*

彭家寅

內江師范學院 數學與信息科學學院，四川 內江 641199

1 引言

量子糾纏作為一種量子資源被用來進行不同類型的量子信息處理，如量子隱形傳態[1-4]、量子超密編碼[5]、量子態分享[6-9]、遠程態制備[10-12]、量子信息凝聚[13]等。由Bennett等[1]在1993年首先提出的隱形傳態是將一個任意單量子未知態從一個地方傳送到另一個遙遠的地方，而沒有該量子自身在空間中的物理傳送。在這開創性工作之后，一些研究者利用不同類型的量子信道，設計出了許多隱形傳態協議[3-9]。最近，Zha等[14]提出了雙向受控隱形傳態方案：信息傳輸的兩方在第三方的控制下，可以同時交換他們的任意單量子未知態。此后，一些學者提出以不同量子糾纏態為信道的相互傳輸量子態的若干方案[15-21]，其中非對稱的雙向受控隱形傳態方案是由Zhang等[18]于2015年首先提出的，該方案以7-量子最大糾纏態為信道，在監控者的控制下，Alice可以傳送她的單量子態給Bob，同時Bob也能傳遞他的任意二量子態給Alice。近幾年來，這方面的研究得到了發展[19-21]。

2000年，Lo率先提出遠程態制備的概念[10]，它是已知量子態的隱形傳態，即通過事先分享量子糾纏和適當測量以及經典通信，發送者能夠為遙遠的接收者制備一個已知量子態。到目前為止，出現了許多不同的遠程態制備方案，如確定的遠程態制備[22-23]、聯合遠程態制備[24-27]、受控的遠程態制備[28-29]、雙向受控遠程態制備[30-31]、多跳受控遠程態制備[32]、循環遠程態制備[33-34]等。一些研究者分析了在受控遠程態制備中監控者的控制能力問題[35]，而一些遠程制備方案已經實驗實現[36-38]。2013年，Cao和Nguyen[31]提出了第一個受控雙向遠程態制備方案，在該方案中，Alice和Bob通過局部操作和經典通信，就能同時交換他們的單粒子量子態。此后，Sharma等[39]提出了概率的、確定的和聯合的受控雙向遠程態制備三個方案。Peng等[30]于2015年雇傭8-量子糾纏態作為信道，提出五方聯合受控雙向遠程態制備協議。2017年，另一個五方聯合受控雙向遠程態制備方案被Wang等[40]提出，該個方案是以7-量子糾纏態為信道的。2016年，Zhang等[41]提出以6-量子非最大糾纏態為信道的聯合受控雙向遠程態制備方案。上述方案是對稱的，即利用不同量子糾纏信道，發送者能夠同時給對方制備單粒子量子態。近年來，一些非對稱受控雙向遠程態制備被提出。2017年，Sang等[42]提出了一個非對稱雙向遠程態制備協議，一個未知單量子態被傳輸，同時一個已知量子態被制備。Song等[43]給出了一個對稱的雙向遠程態制備方案，兩個單粒子態同時被交換。他們還提出一個單粒子態和一個任意二粒子態被制備的非對稱雙向遠程態制備協議。2018年，Fang等[44]提出一個雙向混合量子信息傳輸方案，一個任意未知單粒子態被隱形傳輸給Bob，同時一個已知二粒子態在Alice處被制備。

本文研究9-量子團簇態在非對稱雙向隱形傳態、非對稱雙向遠程態制備、雙向量子信息混合傳輸中的應用，給出三個不同類型的量子信息傳輸協議，指出各方案的特點，并討論實驗實現的可行性。

2 二量子態和三量子態的非對稱雙向隱形傳態

假設Alice想要把未知三量子態式（1）傳送給Bob。

其中，x和y是滿足歸一化條件|x|2+|y|2=1的任意復系數；同時Bob也打算將如下二量子態式（2）傳遞給Alice。

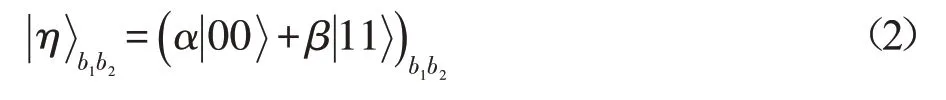
這里α和β是任意復系數且滿足|α|2+|β|2=1。Alice和Bob事先安全地分享如下一個9-量子團簇態[21]：

其中，量子1、3、5、9屬于Alice，而量子2、4、6、7、8屬于Bob。

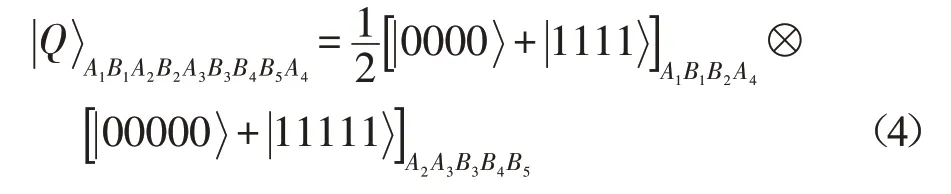
這里，量子A1、A2、A3、A4屬于Alice，而Bob擁有量子B1、B2、B3、B4、B5。

由所有14個量子構成的初始復合態為：

下列8個GHZ-態構成三粒子正交基：

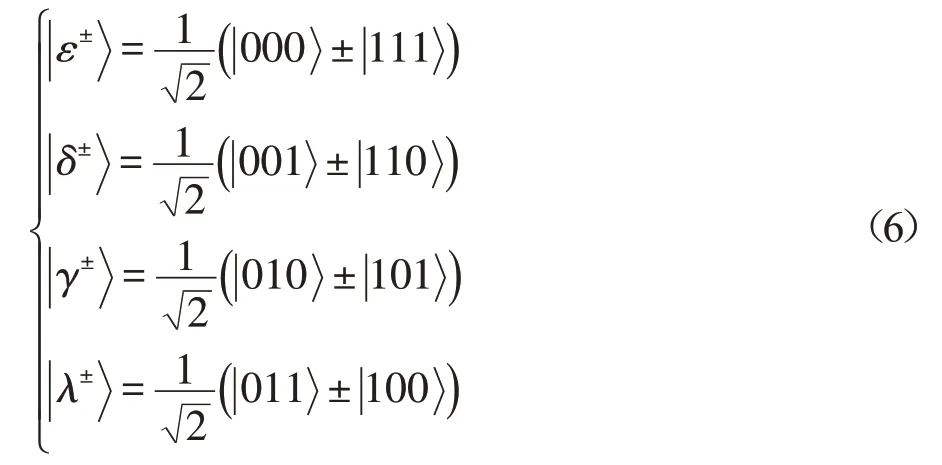
而Bell正交基由下列向量構成：

記Pauli算子：

為完成量子任務，首先Alice需用式（6）所示的GHZ-態對粒子a1、a2和A2進行三粒子測量，然后對粒子A3施行Hadamard門H運算，這里：

再對粒子a3和A3進行Bell-態測量，并將測量結果通知Bob。具體如下：

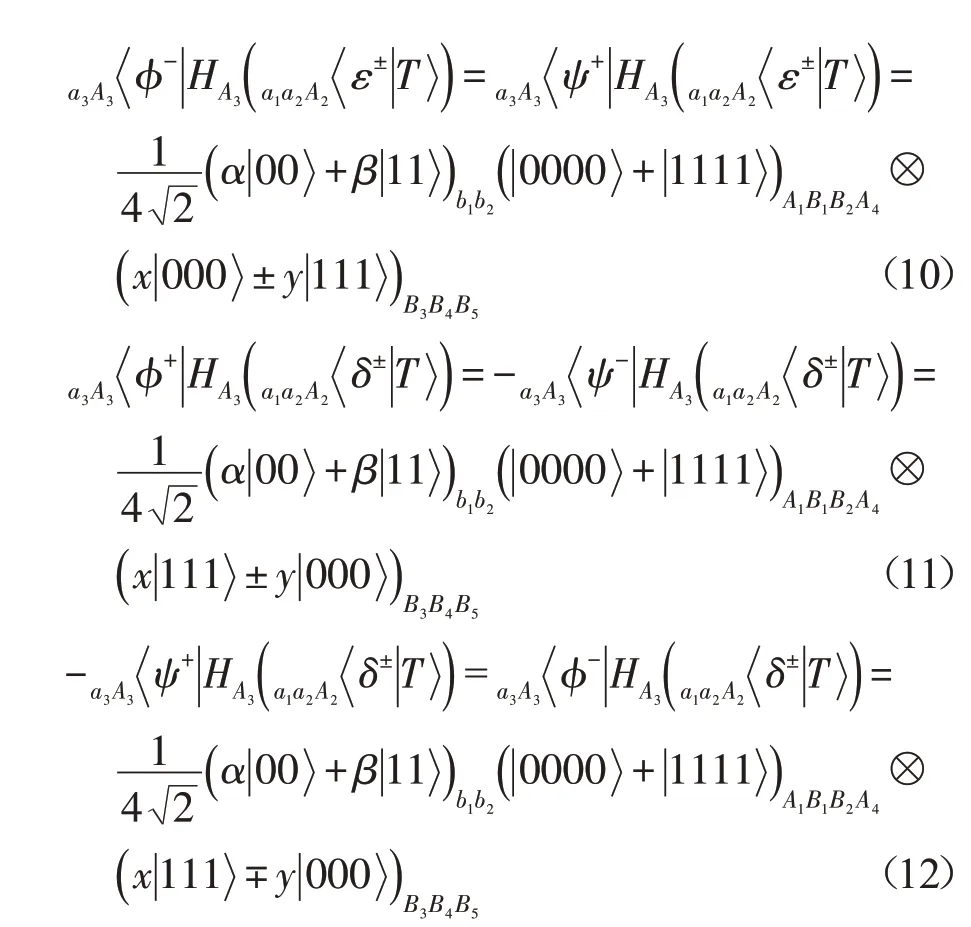
其次，Bob對粒子b1和B1進行Bell-態測量，然后對粒子B2施行Hadamard門H運算，再對粒子b2和B2進行Bell-態測量，并將測量結果告知Alice。具體如下：

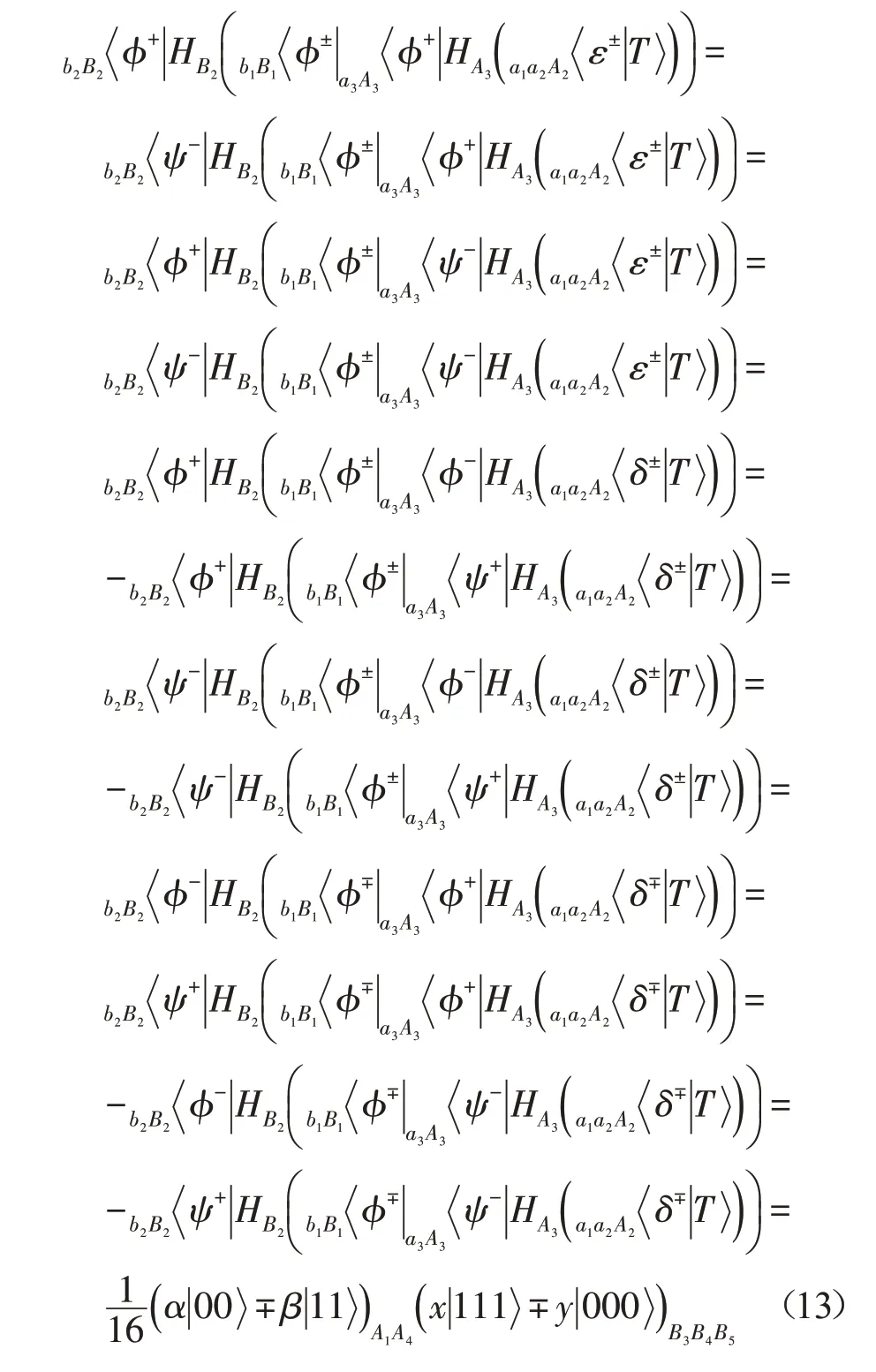
最后，由等式（13）至等式（20）可知，Alice和Bob根據收到的信息，對各自的粒子采用適當的Pauli運算就可以恢復目標態。例如：如果Alice的測量結果為，Bob的測量結果為，則剩余粒子塌陷態為：

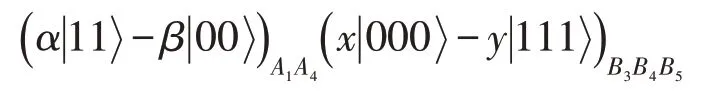
收到測量信息后，Alice對粒子對(A1,A4) 執行iσy?σx運算，Bob對粒子對(B3,B4,B5)施行σz?I?I運算，就可以得到：

從而Alice和Bob同時交換了他們的量子態。對于其他情形，也能得到相同的結論。這樣，本文協議就成功地實現了，且因參與者交換的量子數不同，故本文方案是非對稱的。

注1Alice需用式（6）所示的GHZ-態對粒子a1、a2和A2進行三粒子測量，僅出現的測量結果，這就使得方案簡化了一半。

3 二量子態和三量子態的非對稱雙向遠程制備

考慮如下情景：Alice想要在遙遠的Bob處制備已知三量子態：

其中，x和y是滿足x2+y2=1的任意實系數，θ∈[0,2π]；同時Bob打算為Alice制備已知二量子態：

這里，α和β是任意實系數且滿足α2+β2=1，ω∈[0,2π]。連接Alice和Bob的量子信道為式（4）所示的9-量子團簇態，其中量子A1、A2、A3、A4屬于Alice，而Bob擁有量子B1、B2、B3、B4、B5。

為了完成此量子任務，Alice利用單粒子測量基式（23）測量粒子A2。

再采用前饋測量策略測量粒子A3，即如果Alice對粒子A2的測量結果為則對粒子A3的測量基為：

否則，對粒子A3的測量基為：

從式（26）可知，Alice和Bob根據收到的信息，應用適當的Pauli運算就可重構目標態：

也就是，Alice和Bob相互成功地制備所希望的量子態。所有測量結果及其對應的恢復運算間的關系見表1。

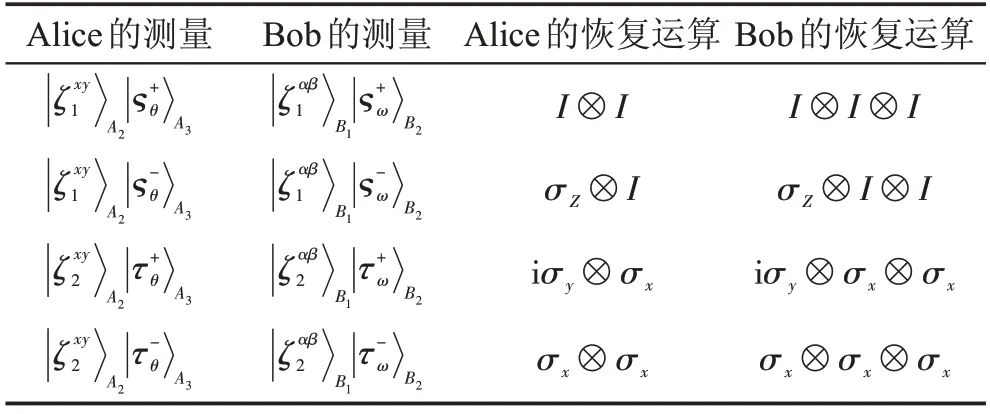
Table 1 Relationship between various measurement results and corresponding recovery operations表1 各種測量結果及其對應恢復運算之間的關系

注2本方案使用了前饋策略，使得方案完美實現。否則，方案成功的概率為26%。

4 二量子態制備和三量子態傳輸的混合非對稱雙向通信

假設Alice想要未知三量子態式（27）傳送給遙遠的Bob。

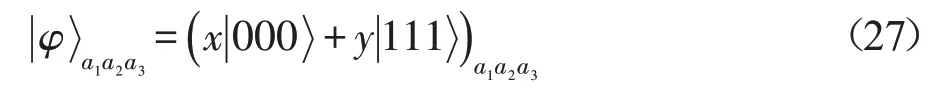
其中，x和y是滿足|x|2+|y|2=1的任意復系數；同時Bob也打算在Alice處制備已知二量子態：

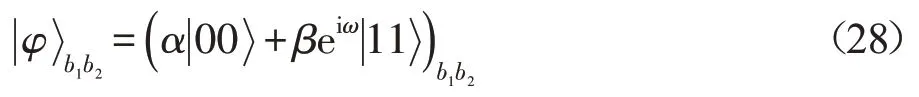
這里，α和β是任意實系數且滿足α2+β2=1，ω∈[0,2π]。連接Alice和Bob的量子信道為式（4）所示的9-量子團簇態，其中量子A1、A2、A3、A4屬于Alice，而Bob擁有量子B1、B2、B3、B4、B5。初始系統為：

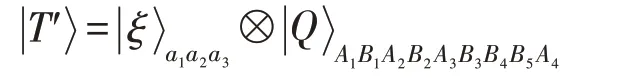
為完成此量子任務，首先Alice對粒子a1、a2和A2進行GHZ-態測量，然后對粒子A3施行Hadamard門H運算，再對粒子a3和A3進行Bell-態測量，并將測量結果通知Bob。其次Bob利用基測量粒子B1，再用前饋測量策略測量粒子B2，即如果Bob對粒子B1的測量結果為，則用基測量粒子B2；否則，用測量粒子B2。最后將測量結果告訴Alice。

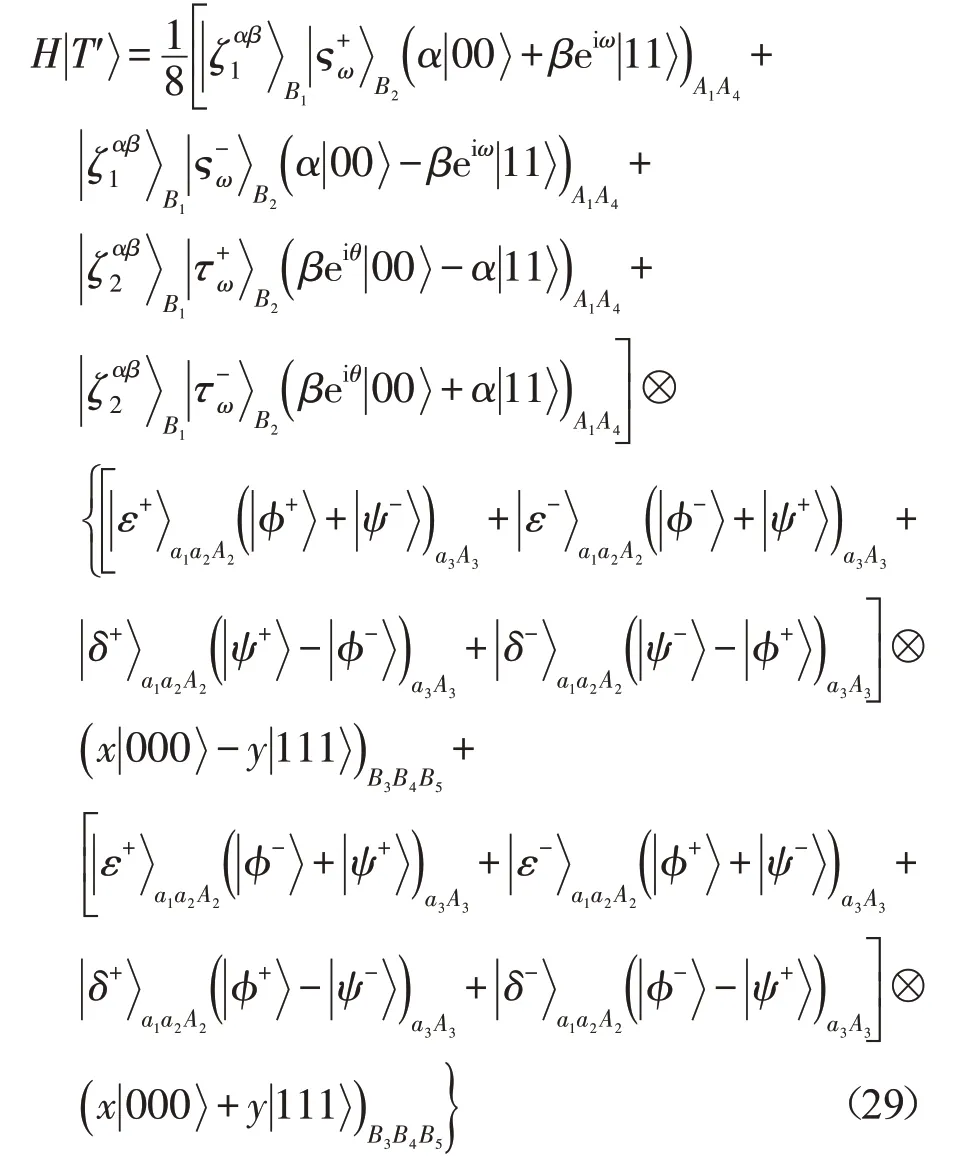
從式（29）可以看出，當Alice聽到來自Bob的測量信息后，她對粒子對(A1,A4)應用I?I或σZ?I或iσy?σx或σx?σx就能獲取；Bob根 據Alice的測量結果，利用變換σZ?I?I或I?I?I，就能得到。也就是，Alice和Bob的信息交換成功，混合量子通信任務成功完成。

注3本方案本質上是前兩個方案的部分結合，因此它具有前兩個方案的優點。類似地，容易獲得二量子態傳輸和三量子態制備的混合協議。

5 結論

本文中三個不同類型的協議的主要資源是同一糾纏信道，其制備是量子通信理論的一個重要方面。有幾種產生糾纏的實驗方法，其中一些方法在文獻[45-47]中提到。此外，還有糾纏集中協議[46-47]，通過它可以在某些情況下增加糾纏量。以9-量子團簇態為信道，分別給出了兩粒子態和三粒子態的雙向隱形傳態、雙向制備以及傳態與制備混合這三個不同類型的協議。在第一個協議中，Alice把自己的未知三量子態傳遞給Bob，同時Bob把自己的未知二量子態傳送給Alice。其特點是方案中的GHZ-態測量基僅僅出現一部分可能的測量結果，這就大大簡化了方案。在第二個協議中，Alice在遙遠的Bob處制備了一個三量子已知態，Bob也能在Alice處制備一個已知二量子態。在雙向制備過程中，充分利用了前饋測量策略，完美地完成任務。在第三個協議中，Alice將一個未知三粒子態傳送給遙遠的Bob，同時Bob也制備一個已知二量子態給遠方的Alice。此方案吸取了前兩個方案的優點，使得它既簡單又高概率地完成量子任務。上述方案需要簡化的三粒子策略、Bell測量、單量子測量、Hadamard門和Puali算子就能夠以100%的概率重構原始二量子和三量子態。就目前的光學技術而言[5，11，30]，本文所涉及的運算都能物理實現。