軌道交通票價定制選擇研究
——基于區間值直覺模糊多屬性決策方法

王冬輝

（湖南交通職業技術學院， 湖南 長沙 410132）

軌道交通票價定制對于城市交通運輸結構優化、 城市資源有效配置、 政府財政負擔緩解等方面都有著舉足輕重的影響[1]。 目前大多數專家學者主要是從票務機制設計以及票制選擇優化兩個方面進行定性研究的。

票務機制設計研究主要分析各種票制特征及其對票務政策的影響。 2004 年， KATHERINE 等[2]研究了各類型公共交通方式的收費種類及水平， 如軌道交通、 常規公交等， 對公交服務水平、 公交出行比例變化與公交收費三者之間的關系進行了定性分析。 2006 年， ZHANG 等[3]通過深入分析英國 6 個城市的票務政策， 基于調查數據， 研究了出行者對票務政策的敏感性等問題， 在此基礎上， 提出了公共交通的票務優化政策。 2008 年， 賀崇明等[4]與蔣惠園等[5]學者討論了我國經濟較發達城市的票制票價體系， 分析了目前我國票制票價存在的不足。

交通票制選擇研究主要分析各種票制優缺點并建立相關選擇模型。 2008 年， 張寧等[6]針對現行各類票制的優缺點進行分析， 指出應當建立 “一卡通” 的票制體系。 2010 年， 周明保等[7]提出了一個新的多層多屬性決策模型， 并將其應用于軌道交通票制選擇。 在實際情況下， 因信息不完全等因素的影響， 軌道交通票制選擇具有一定的模糊性和不確定性， 這使得軌道交通票制選擇成為不完全信息下的不確定決策問題。

由于信息缺失等情況， 決策問題常伴隨著不確定性， 1965 年， ZADEH[8]提出了模糊集理論， 模糊集很好地刻畫了模糊信息， 有效地解決了不完全信息下的決策問題， 模糊集理論成為不確定決策中的研究熱點。 區間值模糊集 （Interval-Valued Fuzzy Sets， IVFSs）[9]， 直 覺 模 糊 集 （Intuitionistic Fuzzy Sets， IFSs）[10]， 區間值直覺模糊集 （Interval-Valued Intuitionistic Fuzzy Sets， IVIFSs）[11]以及 Vague 集[12]也隨之被提出。 區間值直覺模糊集是其中應用較為廣泛的一種模糊集合。 在區間值直覺模糊多屬性決策方法中， 熵計算是關鍵問題。 2001 年， BURILLO和BUSTINCE[13]提出了區間值模糊集熵的概念。2001 年， SZMIDT 和 KACPRZYK[14]解釋了非概率類型的熵測度模型。 2006 年， HUNG 和 YANG[15]基于概率的概念， 定義了區間值模糊集熵和直覺模糊集 熵。 2011 年， WEI 等[16]為 克服 2001 年 SZMIDT等[14]， 2007 年 WANG 等[17]和 2005 年 HUANG 等[18]提出的3 種熵測度方法的獨立定義的缺陷， 給出了新的區間值模糊集熵測度方法。 此后， 區間值模糊集、 Vague集、 直覺模糊集等模糊集合的模糊集熵公式也陸續提出。

針對Vlachos 熵測度方法的不足， 本文先引入猶豫度對其進行改進， 并證明了新的區間值直覺模糊集熵的相關性質， 再基于改進的區間值直覺模糊集熵和IVIL-WGA 算子構建了一個新多屬性決策方法， 以建立一個新的軌道交通票制選擇決策方法， 最優化軌道交通票價選擇方案。

1 區間值直覺模糊多屬性決策方法及改進Vlachos 熵

1.1 區間值直覺模糊多屬性決策方法的基礎模型

定義1[10]： 設X 為給定論域， 則該論域上的直覺模糊集A 簡記為IFS(X) ， 可表示為

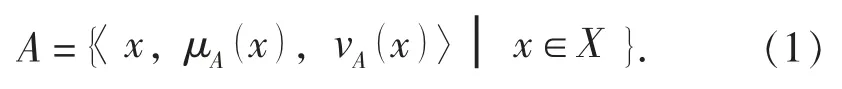
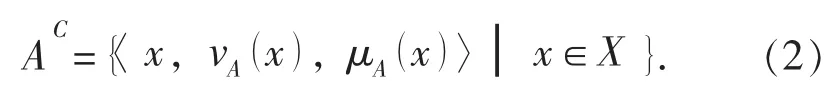
定義 2[11]： 設非空集合則X 上的一個區間值直覺模糊集定義為

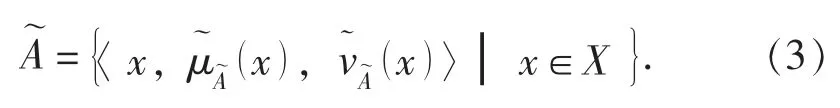
此外， 區間值直覺模糊集也可表示為

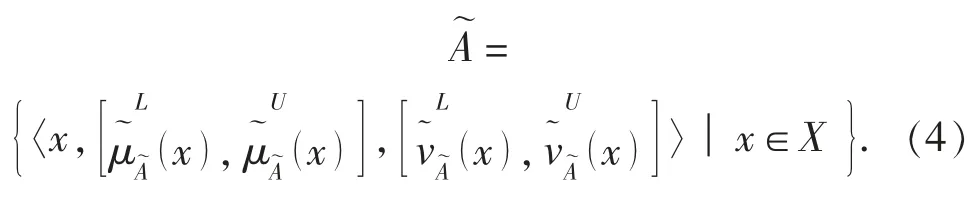
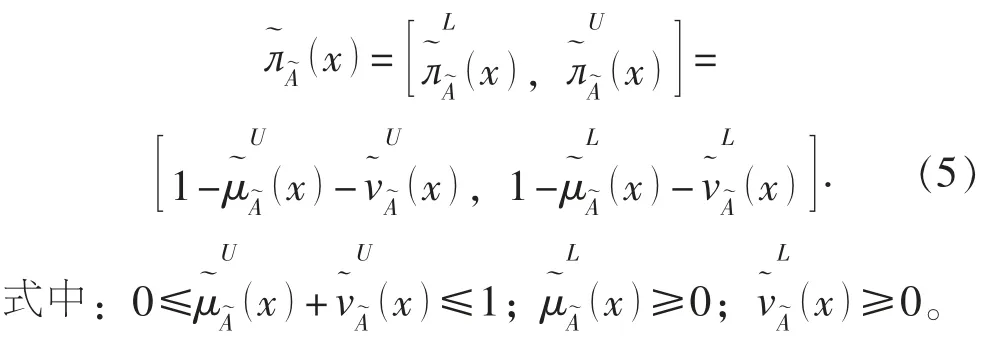
定義 3[10]： 設則， 一是當且僅當二是當且僅當

定義 4[19]： 設則區間值直覺模糊數的加權幾何平均算子， 即IVIF-WGA 算子可表示為

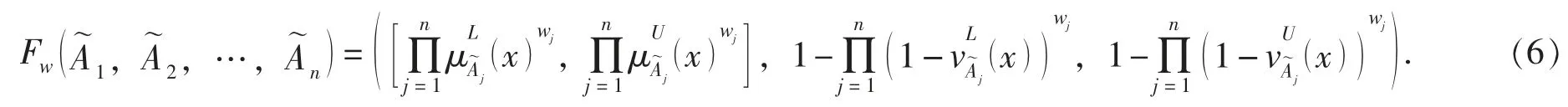
定義 5[11]： 設任意區間值直覺模糊數=的得分函數為

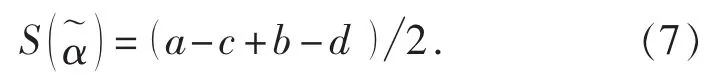
命題 P1： E(A) =0， 當且僅當A 是明確集合。

命題 P3： E(A )=E (AC)， xi∈IVIFS(X )。

命題 P4： E(A )=E(B )， 例如， μAL(xi)≤vAL(xi)， μAU(xi)≤vAU(xi)且 A?B， xi∈X； 或 μAL(xi)≥vAL(xi)， μAU(xi)≥vAU(xi)且 B?A， xi∈X。

1.2 Vlachos 熵的局限性

設E (Ai)是區間值直覺模糊集熵——Vlachos熵， 其測度定義為

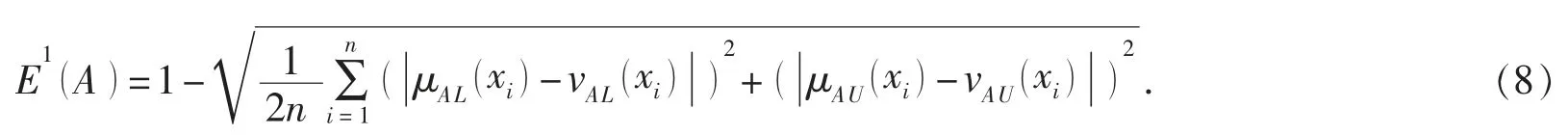
例1： 設有兩個區間值直覺模糊數A=（[0.4，0.5]， [0.1， 0.2]）與 B=（[0.2， 0.3]， [0.1， 0.2]）。 通過比較隸屬度與非隸屬度可知， B 比A 更加模糊。而采用式 （8） 計算E1(A )和E1(B )可得

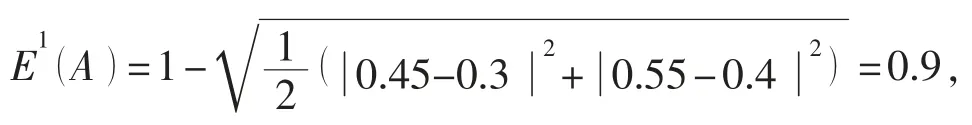
1.3 基于猶豫度的區間值直覺模糊集熵改進

定義 7： 設 A∈IVIFS(X) ， 區間值直覺模糊集熵的測度方法可以定義為

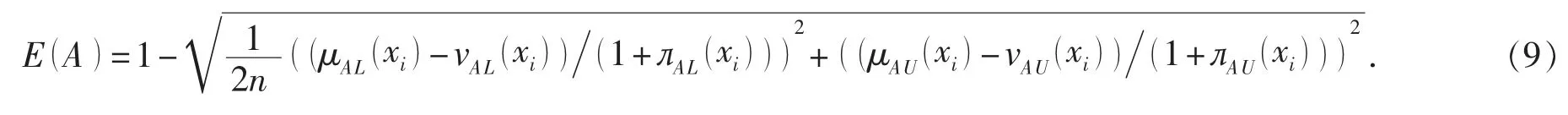
定理 1： 由式 （9） 定義的映射 E(A) ， 是區間值直覺模糊集熵的測度方法。

證明： 式 （9） 作為區間值直覺模糊集熵適合的測度方法， 必須滿足定義6 中命題P1～命題P4。

命題 P4： 為了使式 （9） 滿足命題 P4 的要求，需要證明以下不等式方程

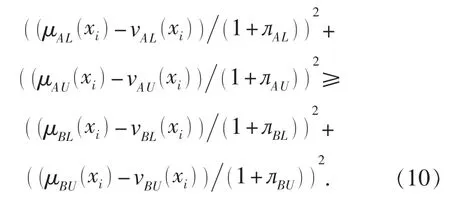
已知函數E 是單調遞減的， 假設μBL(xi)≤vBL(xi)， μBU(xi)≤vBU(xi)且 A?B， 為了證明式 （10），需要證明以下不等式方程組

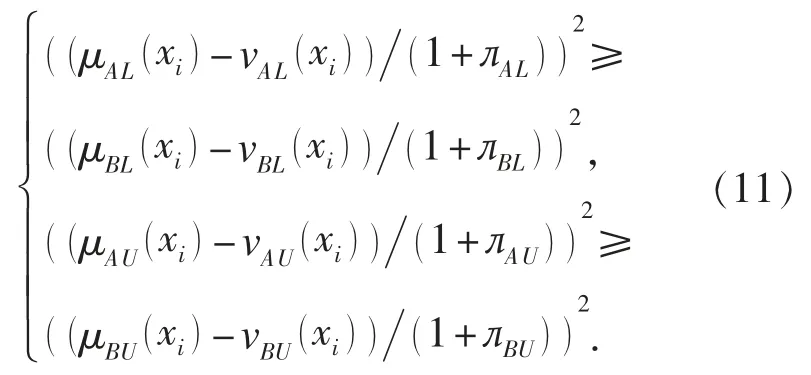
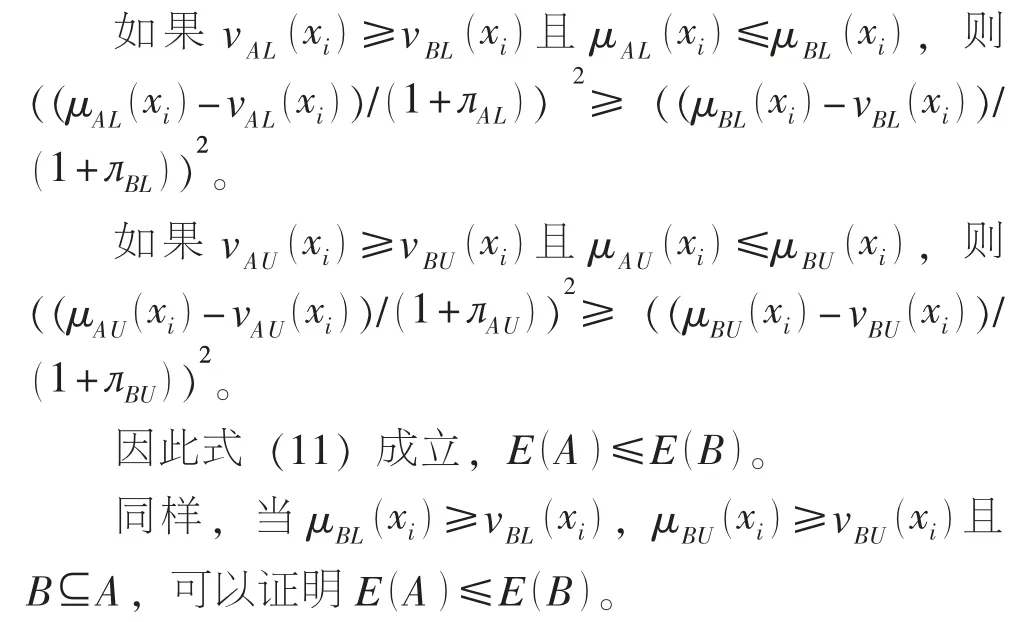
2 新的多屬性決策方法構建

基于上述改進后的區間值直覺模糊集熵和IVILWGA 算子， 本文構建了一種新的多屬性決策方法。對于一個區間值直覺模糊多屬性決策問題， 設有n個方案 X={x1， x2， …， xn}， m 個決策屬性 C={c1，c2， …， cm}， 對應的權重向量為 W= [w1w2…權重向量W 信息不完全， 且[w1w2… wn]T∈δ。 在屬性 cj下， 方案 xj的屬性值 （評價值） 表示為區間值直覺模糊數構成決策矩陣假設決策者態度為風險中立，要求對方案進行排序。 解決該多屬性決策問題的步驟可分為以下4 步。

2） 構建多屬性決策的線性規劃模型。 基于模糊集熵越小則決策信息量越多 （方案越優） 的原則， 本文建立決策模型， 目標函數為

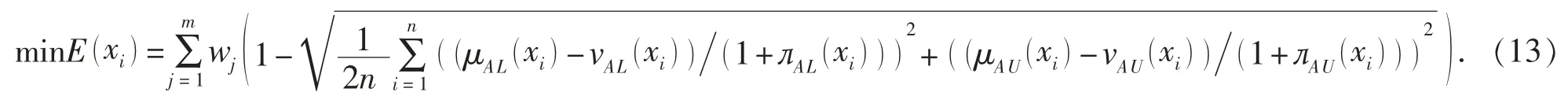
約束條件為[w1w2… wn]T∈δ。

設各方案公平競爭， 則每個方案的模糊集熵屬于同一組屬性權系數， 綜合所有方案的模糊集熵，可得目標函數為

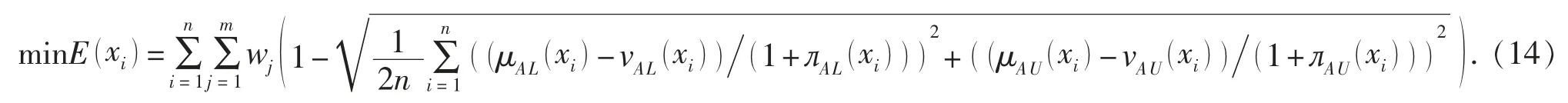
約束條件為[w1w2… wn]T∈δ。

通過線性規劃求解以上模型， 可得到最優解。

3） 采用 IVIL-WGA 算子集結方案綜合屬性值， 得到各方案的綜合屬性值。

3 新多屬性決策方法在軌道交通票制選擇的應用

針對票制選擇多屬性決策問題， 本文對某城市軌道交通情況進行實際調查， 由該領域專家進行評分， 計算得出各個屬性的權重值 （見表1） 和屬性值 （見第 48 頁表2）。

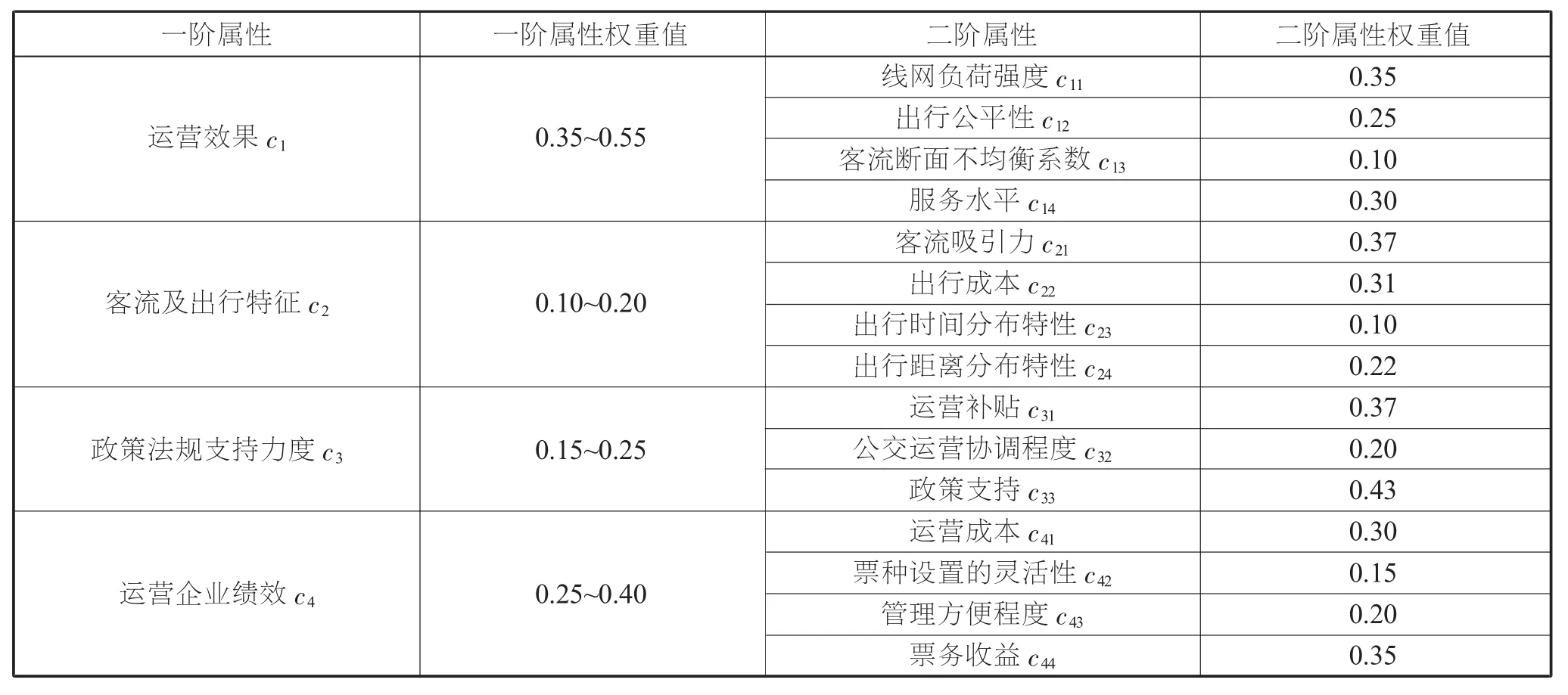
表1 某城市票制選擇多層多屬性決策屬性及其權重值

按照本文構建的多屬性決策方法， 對相關結果計算為： 一是規范化處理。 由表1 可知， 客流斷面不均衡系數c13、 出行成本c22和運營成本c41為成本型屬性， 故采用式（9）對其進行轉化， 結果見第48頁表3。 二是集結二階屬性。 利用IVIF-WGA 算子對二階屬性值進行集結， 得到一階的區間值直覺模糊值， 見第 48 頁表 4。 三是根據表 4 中的數據，采用式 （8） 計算各方案屬性下的區間值直覺模糊集熵， 見第 48 頁表 5。

建立模型， 目標函數為

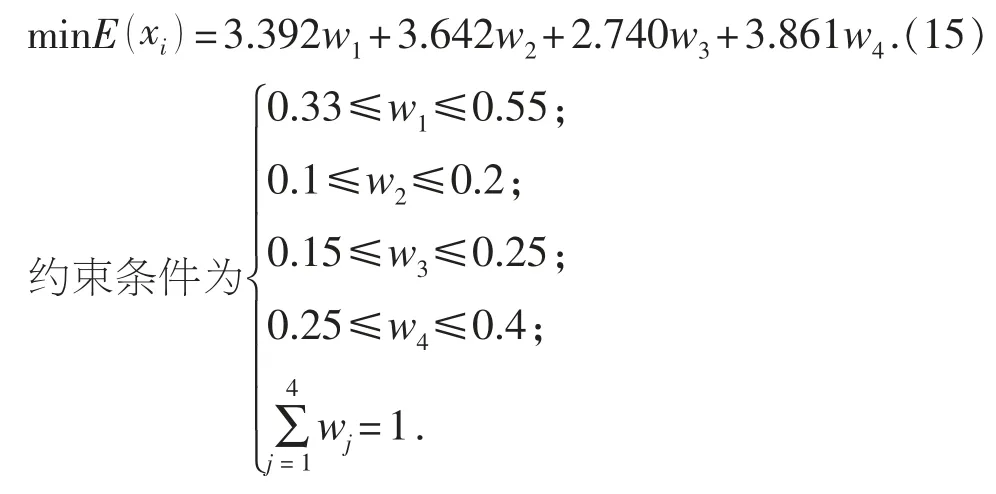
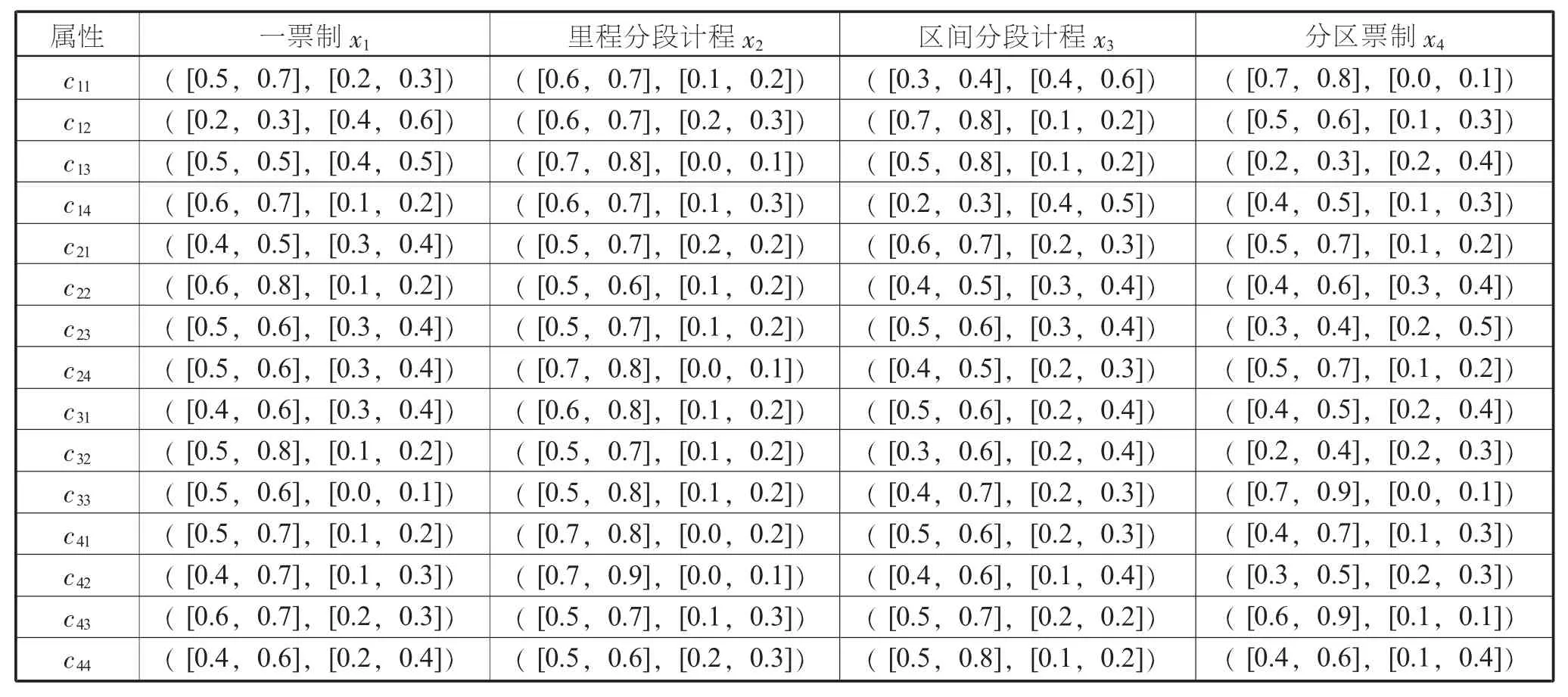
表2 某城市票制選擇多層多屬性決策屬性值

表3 規范化后的成本型屬性值

表4 一階屬性的區間值直覺模糊值

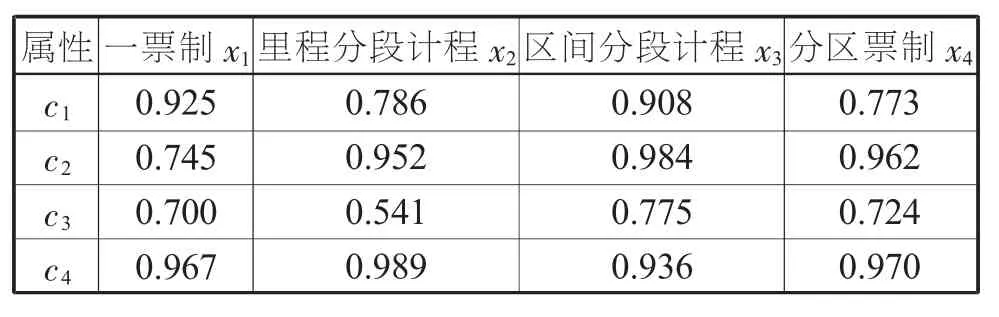
表5 一階屬性的區間值直覺模糊集熵

對模型進行求解， 得到最優屬性權重向量W=[0.4 0.1 0.25 0.25]T。

四是集結方案綜合屬性值， 并對方案進行排序。 利用IVIF-WGA 算子對綜合屬性值進行集結， 得到綜合區間值直覺模糊值（[0.40， 0.53]， [0.18， 0.35]）。

計算并比較各綜合屬性值的得分值的大小， 并對方案進行排序， 可得由于排序結果為 x2＞x4＞x1＞x3， 因此各類型票制的優劣排序為： 里程分段計程＞分區票制＞一票制＞區間分段計程。 由此可見， 里程分段計程是最優選擇。

考慮到軌道交通票制選擇中信息的模糊性與不確定性， 本文提出了基于改進的區間值直覺模糊集熵的多屬性決策方法， 并將其應用于票制選擇問題中， 實例驗證了該方法的有效性。 首先， 針對Vlachos 熵測度模型的不足之處， 提出引入猶豫度對該模型進行改進， 進而提出了新的區間值直覺模糊集熵， 并論證了其相關性質； 其次， 運用改進的區間值直覺模糊集熵和IVIL-WGA 算子， 構建了一個新的多屬性決策方法； 最后， 將該多屬性決策方法應用于軌道交通票制選擇問題。 準實驗研究方法用于預算績效管理也有其局限性， 一是大部分準實驗研究更適用于上級對下級進行戰略層面的整體評價，而用于單個項目預算進行自評時則欠佳。 二是準實驗研究需要大量的數據支持， 因此需耗費較多的時間和資金成本。 三是由于并非所有政策事件的數據都可以模擬隨機安排， 因此并不是所有政策事件都可以使用該方法。 四是該研究中需要未受到影響事件影響的對照組， 如某政策事件全面放開， 則沒有對照組可言， 也就無法用準實驗研究做出評價。

綜上所述， 我國預算績效管理經過若干年的摸索與實踐， 已經形成了一套較為完整的管理模式。這套管理模式既吸收了國外的經驗， 又緊密結合了我國的行政實踐， 但仍存在改進和發展的空間。 當下， 預算績效管理進入了嶄新的階段， 同時也是創新發展的關鍵時期， 將預算績效管理與經濟學研究方法相結合， 也不失為一種有益的嘗試與創新。