導數在近年高考壓軸小題中的應用
趙愛華
(新疆烏魯木齊市教育研究中心 830002)
導數及其應用是高中數學的重要教學內容,也是高考重點考查內容.近年來,全國卷在選擇題的第12題,或填空題第16題陸續出現導數壓軸小題,考點設置或明或暗,全面考查高中數學主要內容.我們不妨來分類研究,以提高我們教學的針對性和有效性.
一、導數在三角函數中的應用
例1(2018年高考數學全國Ⅰ卷理科第16題)已知函數f(x)=2sinx+sin2x,則f(x)的最小值是____.
分析此題中函數是將正弦函數兩次變換相加而得,第一次縱坐標伸長為原來的兩倍,橫坐標不變;第二次橫坐標縮短為原來的一半,縱坐標不變.題面很熟悉,但是這個加號使得題目變得不同尋常.因此,我們考慮應用導數,找到極值點,求出極值,最后取極小值作為最小值.
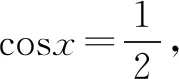
評注本題屬于三角函數創新題,依靠常規的三角運算和方法作答有些困難.通過邏輯推理,幾何直觀可以發現,本函數連續且有界.考查學生應用知識的能力,把極小值轉變為最小值.這里有一定的三角運算,這些正是數學的部分核心素養.
二、導數在立體幾何中的應用
例2 (2017年高考數學全國Ⅰ卷理科第16題)如圖1,圓形紙片的圓心為O,半徑為5cm,該紙片上的等邊三角形ABC的中心為O.D、E、F為圓O上的點,△DBC,△ECA,△FAB分別是以BC、CA、AB為底邊的等腰三角形,沿虛線剪開后,分別以BC、CA、AB為折痕折起△DBC,△ECA,△FAB使得D、E、F重合,得到三棱錐.當△ABC的邊長變化時,所得三棱錐體積(單位:cm3)的最大值為____.
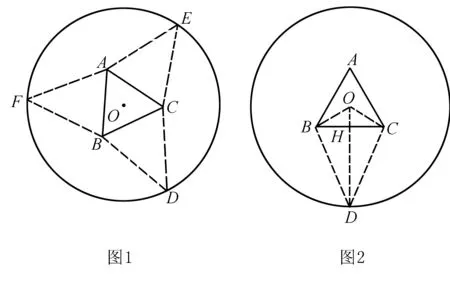
分析連接OD,交BC于H,如圖2,設OH=x,根據各邊的長度關系確定BC,DH,求解三棱錐的高以及△ABC的面積,進而得到三棱錐體積V的解析式.顯然三維空間帶來了高次函數,只有借助導數,才能確定最大值.

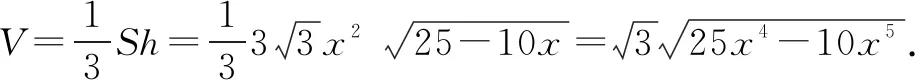

評注本題以立體幾何的折疊問題為背景,考查導數的應用.學生首先要能理解題意,合理設置變量,構造函數,然后應用導數的三大功能:求函數的單調區間、極值、閉區間上最值解決實際問題.數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析六大核心素養都得到了很好地考查.
三、切線在切線問題中的應用
例3 (2016年高考數學全國Ⅱ卷理科第16題) 若直線y=kx+b是曲線y=lnx+2的切線,也是曲線y=ln(x+1)的切線,b=____.
分析切線問題是導數中最常見最簡單的問題,但本題中公共切線把導數基礎知識和整體代換技巧融為一體,把神秘的超越方程等價轉化為可運算的簡單方程,方程組思想使待定系數法能順利實施.
解設直線y=kx+b與曲線y=lnx+2相切于P(x1,y1),直線y=kx+b與曲線y=ln(x+1)相切于Q(x2,y2).

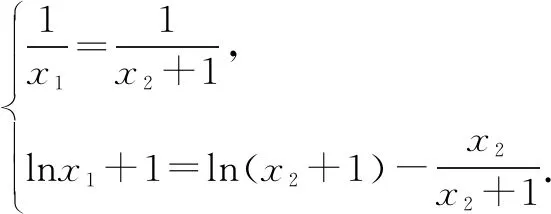
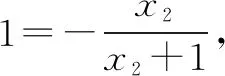
評注本題屬于導數問題中最樸素的問題,但是公切線又賦予了問題新的內涵,融合了一些數學運算技巧,將抽象運算變得可操作,使題目檔次上升,成為小題把關題.數學抽象、邏輯推理、數學運算、數據分析等核心素養融入其中.
四、導數在抽象函數中的應用
例4 (2015年高考數學全國Ⅱ卷理科第12題)設函數f′(x)是奇函數f(x)(x∈R)的導函數,f(-1)=0,當x>0時,xf′(x)-f(x)<0,則使得f(x)>0成立的x的取值范圍是( )
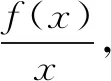
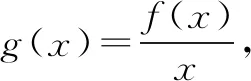
評注本題是抽象函數問題,綜合考查函數和導數的性質,要求學生邏輯推理嚴謹,數據分析到位,數學運算準確,否則極易選成干擾項.本題在導數知識的應用方面是一個很好的范例.對于這種創新試題,試圖通過刷題來提升水平的學生,可能感到棘手.
五、導數在極值問題中的應用
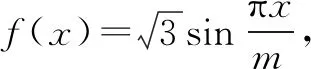
分析從極值點、極值概念入手,從概念中抽象出數據.正確理解存在性,將抽象不等式具體化,合理建模使導數和不等式有效溝通即可求解.
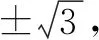
評注本題以三角函數和復合函數為背景,以存在性為依托,考查導數中重要概念極值、極值點.只有概念清晰的學生才能發現[f(x)]2=3,以及解出極值點.導數和不等式的知識巧妙結合,通過正確嚴謹推理,達到解決問題的目的.本題考查了學生綜合運用知識的能力,是以后教學的一個很好的素材.
六、導數在數列中的應用
例6 (2013年高考數學全國Ⅱ卷理科第16題) 等差數列{an}的前n項和為Sn,已知S10=0,S15=25,則nSn的最小值為____.
分析題目表象考查等差數列,但是等差數列的前n項和Sn是關于n的二次函數(公差不為0),那么nSn就是關于n的三次函數,三次函數的最值需用導數求解.注意到定義域的離散型,該三次函數的極值還未必是最值,因此,還要結合單調性才能作答.
解設數列的首項為a1,公差為d,則
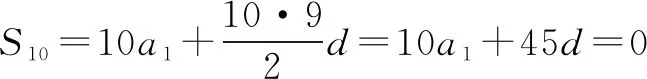
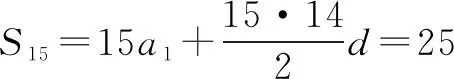
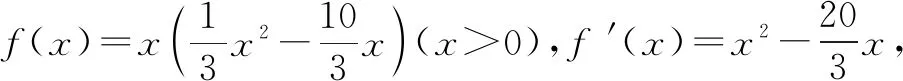
對于nSn而言,n∈N+當n=6時,6S6=-48,當n=7時,7S7=-49,所以nSn的最小值為-49.
評注本題在數列、導數和函數的交匯處命題,導數的應用具有隱蔽性.考查學生是否真正掌握了數列的函數特性,否則無法抽象出這個三次函數.還有三次函數求最值與數列的最值還有區別,也有聯系.這在考查數學抽象、數學建模、數學運算、數據分析等核心素養方面,是一道有高度,且高度適中的好題.
高考中導數的試題視角寬廣,立意新穎,年年推陳出新.選材緊扣教材,高于教材,與高中數學各分支模塊均有聯系,背景靈活多變,設問巧妙.導數重點考查通性通法,突出考查單調性、極值、最值的應用.將“考基礎、考能力、考素質、考潛能”四合一,充分體現了“培養和提高學生的數學核心素養”課程理念,具有較強的區分度,確保高校準確選拔優秀人才.

