在鼓勵中前進 在前進中探索 在探索中完善
——記高三三角函數的一節復習課
任運廣
(云南師范大學附屬中學 650106)
首先,給出例題:

提出要求:請同學們給出盡量多的解法.
同學們進行思考,過段時間后, 我給出第一種解法,
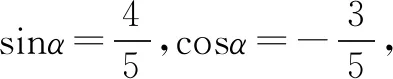
目的有三:其一,活躍課堂氣氛,鼓勵發散思維,間接告訴同學只要能夠得到結果的任何視角,均可與大家分享;其二,肯定跳躍思維,此時思維活躍的同學,在第一時間就能猜得結果;其三,給出結果,明確目標,鼓勵同學們積極參與課堂討論.
待我介紹完,我所謂的解法后,拋磚引玉的效果初現,此時有第一位同學講解了第二種解法,如下:

等同學講解完,適時提出問題:請問同學,你是怎么想到該解法的,或者說該解法中有哪些必然性的規律?

該生在分析的過程中,進行了如下的思維過程:明確目標→轉化問題→方程思想.
該分析得到了同學的認可,教室里也想起了掌聲!
緊接著,繼續詢問,是否還能給出其他的不同解法呢?又一位同學給出了第三種解法,如下:

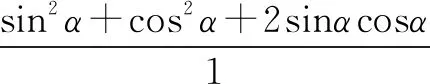
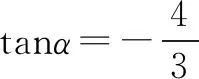
等該同學講解完,我提出兩個問題:
同學回答:第一個問題,我與第一個同學一樣,希望得到tanα的方程,同時也想到了方程sin2α+cos2α=1,既然是sinα與cosα的比值,將1即sin2α+cos2α放在分母上,此時我希望得到一個齊次方程,于是我想到了平方,第二個問題,步驟中應該進行嚴謹的說明,剛才忽略了,主要是借用了前面的結果.
該同學巧妙地運用了sin2α+cos2α=1,構造出了一個特殊的齊次方程,方法巧妙,聯系緊密,綜合思考能力要求較高,只是步驟書寫有待完善.
此時,又有一位同學給出了另外的解法,如下:

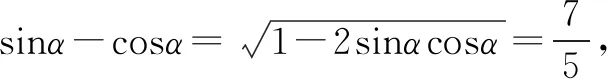

該同學書寫完步驟后,補充到:既然我們要解出sinα與cosα的值,即要得到sinα與cosα的兩個方程,于是由(sinα±cosα)2=1±2sinαcosα,結合α的范圍可以實現sinα+cosα與sinα-cosα之間的聯系,得到上述的解法.
該方法通過平方這個巧妙的運算技巧,將sinα+cosα與sinα-cosα聯系在一起,得到方程,實現問題的解決,書寫步驟完整.
繼續詢問是否有其他的處理方式,有同學給出以下解法:

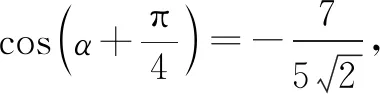
該解法從輔助角出發,看似與目標沒有聯系,待處理完第一步時,再結合已知條件,有種豁然開朗的感覺,有點柳暗花明的味道,比較符合處理問題的思維情景,是接地氣的一種解法.
其思維過程簡述為:對已知條件作出自己能做的處理(處理時并不知道能得到什么樣的效果)→再結合已知條件→發現條件與目標之間的聯系→問題得到解決.
通過前面五種方法的講解,同學的思維逐漸活躍起來,處理問題的方式也得到了啟發,參與的熱情越來越高,陸續有同學介紹了幾種如下方法.

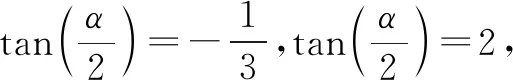

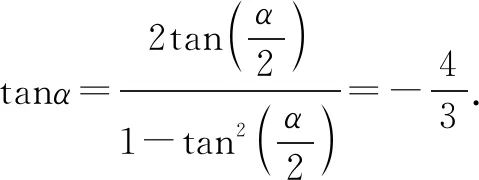

上述的兩種處理問題的過程中,共同選擇了萬能公式作為中間過度,實現了條件與結果之間的聯系,問題得到了解決.這種解法要求對萬能公式有一定的認知,要求較高,拓展了同學們的思維視角,讓同學們體會到了三角恒等變換處理過程中變中不變的真諦,激發了同學們對數學學習的熱情.
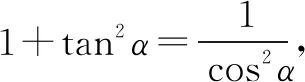
最后我給出了一個解析的方法如下:
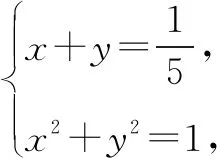
該解法本質上與解法二相同,只是知識展示形式上有所不同,姑且作為一種解法,解法九知識的起點于三角函數的基本概念,回歸本質.
課后反思:高三復習階段,教師選擇例題就應該選擇如本文介紹的例題一樣,可以有處理問題的不同的視角,使不同層次的同學等到相應的發展,通過不同層次視角的探索等到不同的收獲,在收獲中體會學習的快樂!

