基于偽衛星的室內定位算法研究

于雪崗，封 欣，鄧志鑫

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081;2.中國人民解放軍32021部隊，北京 100094)

0 引言

室內定位[1]是當前定位導航領域的一個重要方向，有著各種各樣的應用場景，例如商場內商家精確導航、室內位置共享等模式。為了實現室內定位，目前開發了多種定位手段，包括藍牙定位、WLAN定位[2]、視覺定位、激光定位和慣導定位等多種定位手段，但這幾種定位手段均存在定位精度差的問題。對室外定位來說，GNSS系統[3]目前已經能夠滿足cm級定位需求，利用這一系統原理建造相似的室內定位系統來滿足人們的定位需求，開展室內偽衛星系統定位算法研究，開展使用偽衛星進行室內定位的理論可能性及工程實現，并在當前已有的接收機基礎上進行算法分析及改進，分析偽衛星室內定位中存在的問題及優缺點。

1 室內偽衛星模型

鑒于室內環境布設場地有限，偽衛星布設可以采用陣列的形式來實現，以減小系統設計的空間需求，這樣會產生空間位置精度因子(PDOP)[4]惡化的后果。PDOP只與偽衛星布設和用戶位置有關，與其他因素無關。假設用戶坐標位置為P=(x,y,z),偽衛星坐標位置為Pn=(xn,yn,zn)，由此可以得出幾何矩陣：

(1)

權系矩陣H：

(2)

PDOP為：

(3)

在較為空曠的室內環境中，偽衛星陣元可以懸掛在室內上空，采用八陣元的形式，陣元間隔約為1.3 m，采用七圍一的形式，其結構圖和PDOP分布如圖1所示。

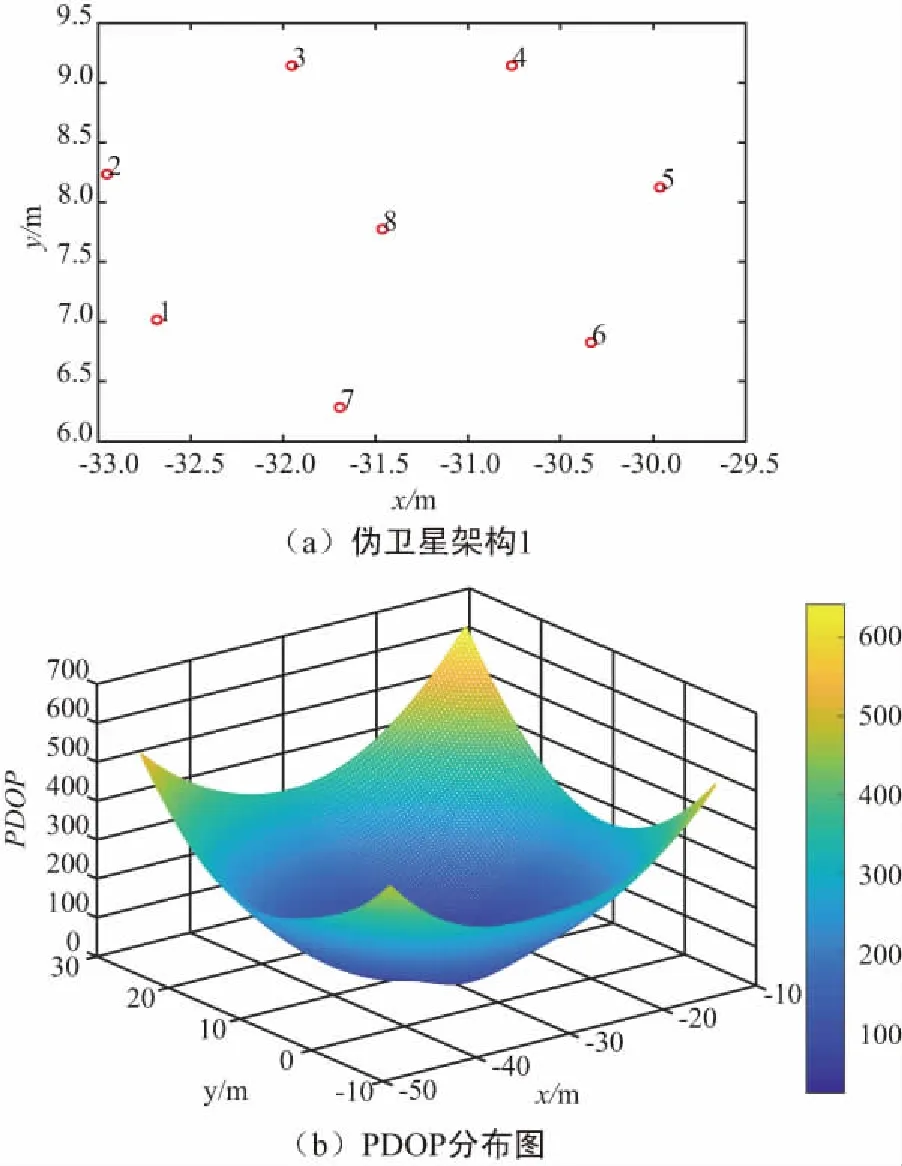
圖1 偽衛星架構1及PDOP分布示意Fig.1 Pseudo_satellite architecture 1 and PDOP distribution diagram

室內環境如果存在狹長的走廊時，偽衛星陣元只能在走廊一側傾斜安裝，陣元間隔約為1.1 m，其結構圖和PDOP分布如圖2所示。

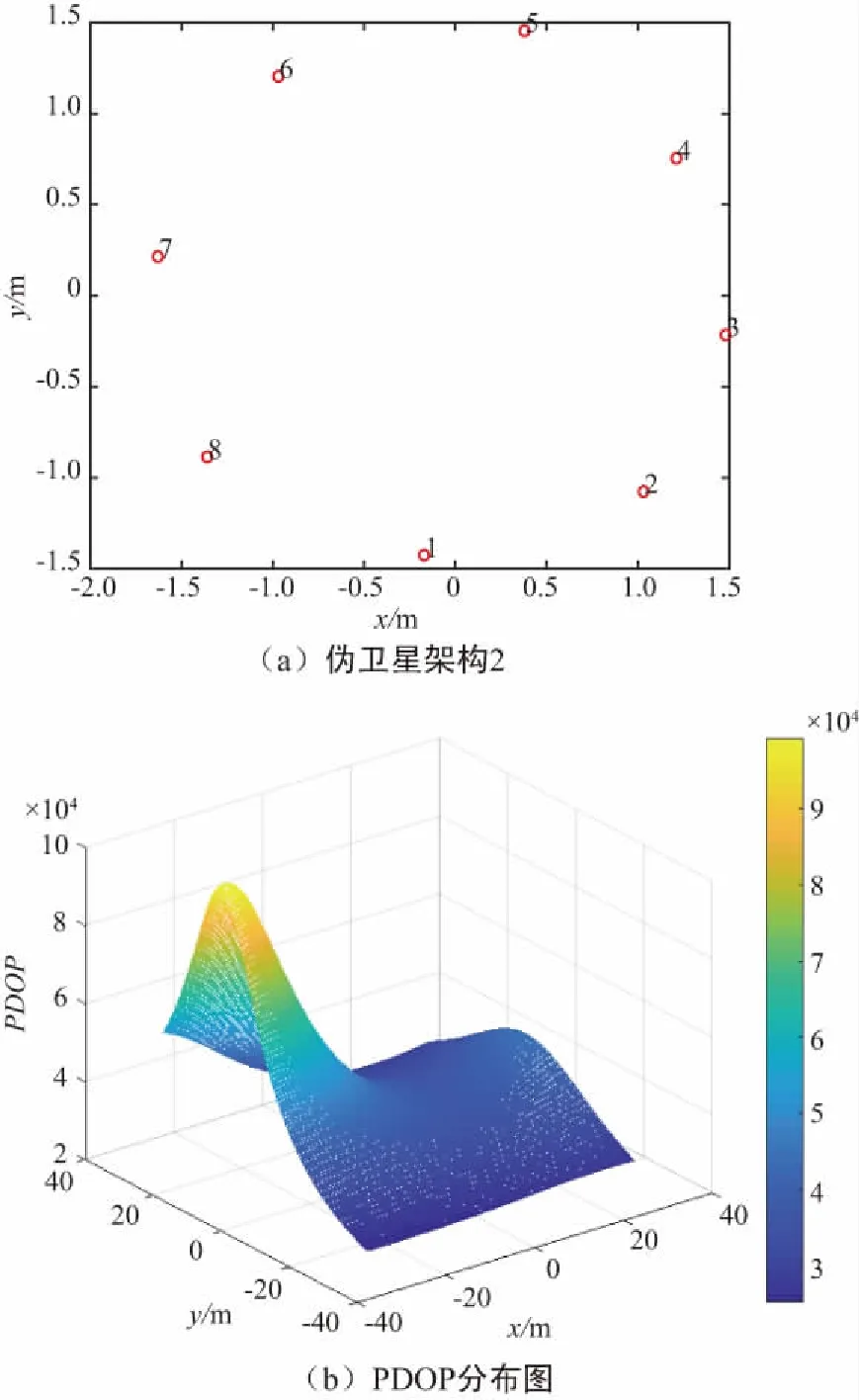
圖2 偽衛星架構2及PDOP分布示意Fig.2 Pseudo_satellite architecture 2 and PDOP distribution diagram

對衛星導航系統來說，為保證定位精度和最小二乘定位算法[5]收斂性，PDOP一般要求小于99，室內環境中大部分區域都不滿足這一特性，引起定位誤差大甚至使用最小二乘定位算法時，定位不收斂的情況。

室內定位中存在的另一個問題在于室內環境復雜，用戶機除了接收到偽衛星直射波以外，還會接收到該直射波多份反射波的斜波，這種反射波對接收機性能的影響成為多路徑效應[6]。假設信號為s(t)，直射信號為A*p(t)*sin(2*pi*f*t)，則存在：

s(t)=A*p(t)*sin(2*pi*f*t)+

(4)

接收信號與本地偽碼相干積分后自相關函數[7]表示為：

(5)

反射波的相位φi具有隨機性，其與直射波的相位關系具有不確定性。由于室內環境相比室外環境[8-9]更為復雜，多路徑效應也更加顯著，出現二次反射波或者多次反射波，嚴重影響自相關函數特性[10-11]，降低碼相位和載波相位精度，進而影響偽距測量精度，降低接收機用戶定位和定速精度。由于載波相位測量值相位[12]誤差最大不超過90°，即1/4波長，誤差為cm級，所以在一定條件下通過載波相位平滑偽距對偽距測量精度有較大的提升作用。在室內環境下對偽距測量值和載波相位平滑偽距值進行測試，其實測結果如圖3所示。

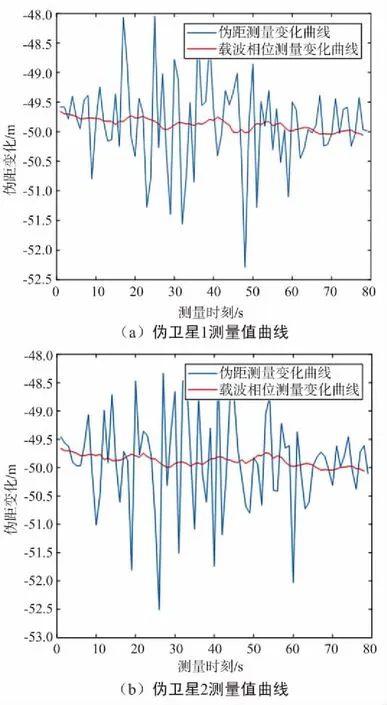
圖3 偽距測量誤差和載波相位誤差示意Fig.3 Pseudo-measurement error curve and carrier phase measurement error curve

由圖3可以看出，相對于偽距直接測量，多路徑效應對載波相位測量值的影響會更小，所以采用載波相位平滑偽距的方式可以減少偽距測量值中的多路徑誤差，同時在接收機中可以通過窄相關處理，多路徑消除等技術手段減少多路徑效應對接收機的影響。

2 遍歷算法

從上述分析可以得出，室內環境存在偽距測量精度低、幾何位置精度因子差的特點，這2種因素會造成最小二乘定位算法發散不收斂，所以這種傳統的定位算法不再適合于室內定位。同時，室內環境存在用戶動態低、高程變化慢的特點，結合這些特點，為了實現室內偽衛星定位功能，開發了一種新的室內定位算法——遍歷定位算法，新算法具有穩定性強，對偽距測量精度要求低的特點。遍歷定位算法主要依據載波相位平滑偽距，在上一個定位點的一定范圍內平面搜索最符合偽距變化規律的位置作為新的定位點，這就要求在室內環境中存在一個基準點位置作為遍歷定位算法的初始值，而室內環境很容易能夠滿足這一要求。遍歷定位算法的流程如圖4所示。

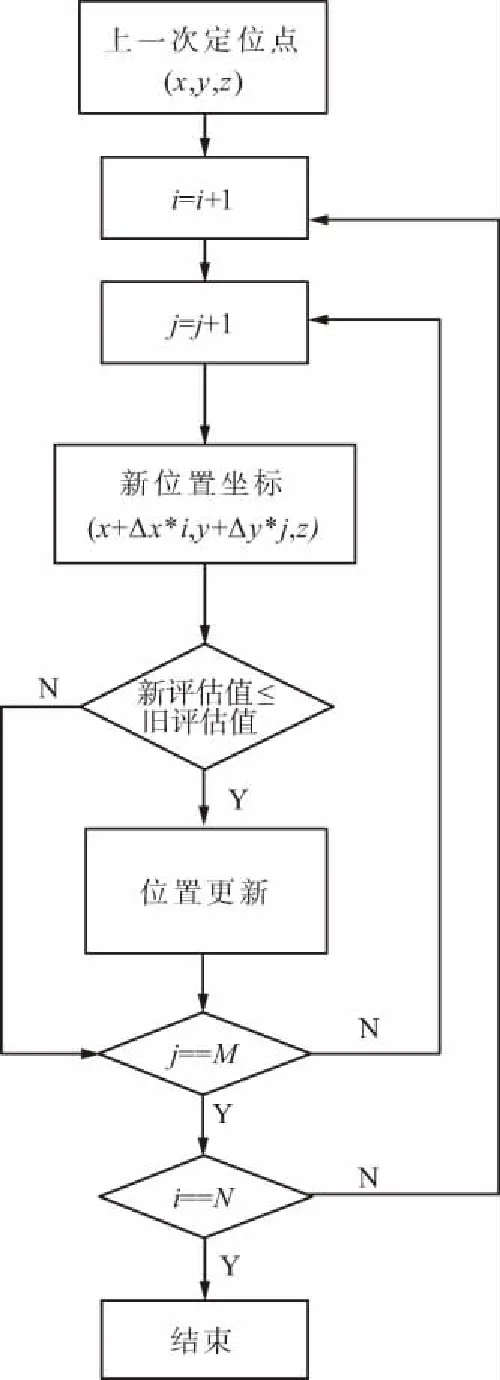
圖4 遍歷定位算法流程示意Fig.4 Traversal localization algorithm flow diagram

圖4中Δx,Δy分別為平面垂直兩方向搜索步長，決定了搜索精度；M,N為步進次數，決定了平面搜索范圍。

通過載波相位得到一組偽距測量值R，通過假設位置點估計另外一組偽距估計值Rt1，通過這2組偽距值計算評估值來評估當前位置是否為最優位置。偽衛星位置為Pn，上時刻偽衛星位置為Pt0=(x,y,z)，下一時刻假設位置為Pt1=(x+Δx*i,y+Δy*j,z)，則有：

(6)

E=R-Rt1,

(7)

式中，E為偽距測量值和偽距估計值之間的誤差向量。實際工程中，接收機和偽衛星中都存在鐘差等一系列共性誤差，為了消除這些誤差對評估值的影響，根據誤差具有共性的特點，對誤差向量E取單差，改進后的誤差向量為：

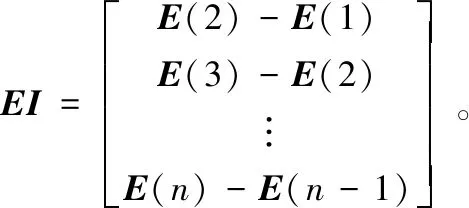
(8)

誤差向量EI表示假設位置點偽距估計值和實際的偽距測量值之間的誤差，其模值越小則和實際坐標點越匹配，在合理范圍內搜索出的最小模值點即為下一時刻的坐標定位點。坐標點誤差分布曲線和投影曲線如圖5所示。

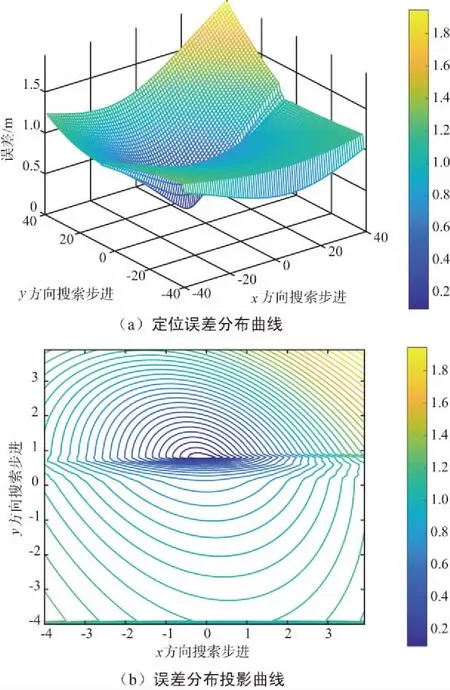
圖5 遍歷誤差分布曲線及投影曲線示意Fig.5 The error distribution curve and projective curve

3 遍歷算法定位結果

相對于最小二乘算法，遍歷算法需要占用更多的資源，而且隨著搜索精度和范圍的提高，搜索所需時間將幾何增長，極大限制了遍歷算法在室內定位中的工程實現。為了滿足室內定位工程需求，需要對遍歷算法搜索范圍和精度進行合理分配，在硬件限制范圍內實現不同精度要求。通過工程測試，其定位效果如圖6(b)所示。

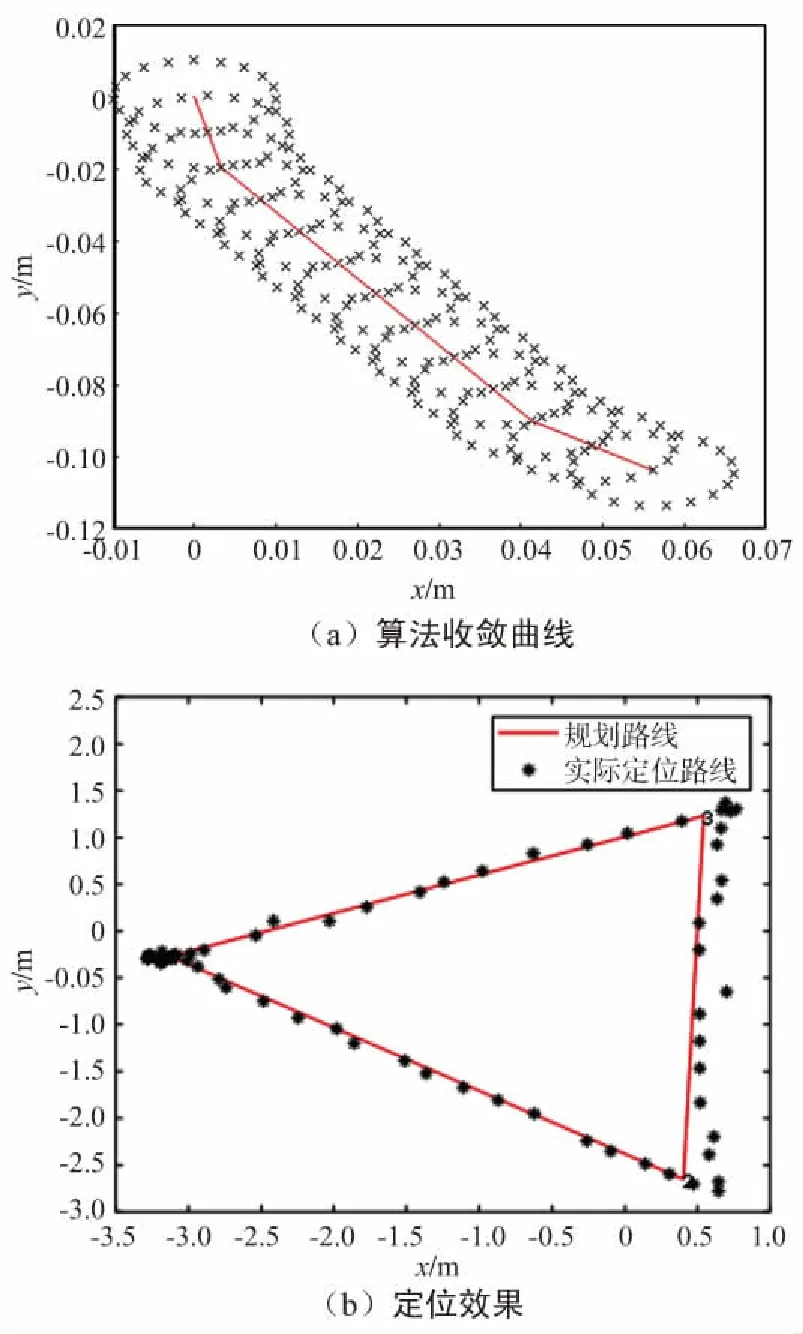
圖6 遍歷算法收斂曲線和定位效果Fig.6 The convergence curve of the traversal algorithm and positioning effect chart

圖6(b)中直線為規劃路線，黑色為遍歷算法定位曲線。實驗證明，遍歷算法定位曲線和實際規劃路線基本重合，定位誤差在0.3 m以內，并且能夠最終在起始點閉合，滿足室內定位精度需求。

4 結束語

目前，室內定位實現手段眾多，為了滿足室內定位需求，采用多元融合的形式進行定位實現。偽衛星室內定位具有精度高、易實現的優點，是當前室內定位的一個重要手段，有很大的發展前景。同時，偽衛星室內定位也存在各種各樣的問題有待解決，尤其是多路徑效應和高程計算問題。