表示學習中句子與隨機游走序列等價性的一種新證明*

孫 燕,孫茂松,趙海興,冶忠林

(1.青海師范大學計算機學院，青海 西寧 810016;2.清華大學計算機科學與技術系，北京 100084; 3.青海省藏文信息處理與機器翻譯重點實驗室，青海 西寧 810008; 4.藏文信息處理教育部重點實驗室，青海 西寧 810008;5.青海民族大學計算機學院，青海 西寧 810007)

1 引言

表示學習是機器進行數據挖掘和數據推薦的基礎。表示學習可以通過神經網絡訓練學習數據特征，并將數據及其關系映射到低維度向量空間中。目前表示學習有詞表示和網絡表示學習，分別應用于自然語言處理和社交網絡的研究中。詞表示學習是通過算法學習建模句子中當前詞語及其上下文詞語之間的關聯關系，而網絡表示學習是通過算法建模當前節點與鄰居節點之間的關聯關系。

詞表示學習中經典的方法是word2vec詞向量[1]，word2vec是2013年由Google的Mikolov團隊提出的用來生成語言模型的工具。它是用淺層的神經網絡訓練并重構語言學的詞和上下文關系的語言模型。

Mikolov等[1]提出word2vec語言模型可以用 CBOW和Skip-Gram 2個淺層的神經網絡模型訓練，并有2個優化方法Hierarchical Softmax和 Negative Sampling加速詞向量訓練速度。

Levy等在文獻[2]中證明了word2vec中負采樣Skip-Gram模型SGNS(Skip-Gram with Negative-Sampling)[1]是對移位正定(非負)互信息SPPMI(Shifted Positive Pointwise Mutual Information)[2]的隱式分解，其中SPPMI矩陣是統計詞和上下文共同出現概率的矩陣，它是對PMI(Pointwise Mutual Information)矩陣的改進。因為互信息是一個比值，還要進行對數運算，分母不能為零，所以計算互信息時需使PMI 矩陣正定，即PPMI矩陣，如果節點采樣時用負采樣,互信息矩陣改進為SPPMI矩陣，進一步加快計算速度。

網絡表示學習中經典的算法是DeepWalk算法，該算法是Perozzi等[3]提出的網絡表示學習模型，將網絡節點關系映射到低維度的向量中，以便人們更好地研究各種復雜網絡。DeepWalk算法可使用Skip-Gram模型建模網絡節點之間的關系，并可采用Negative Sampling方法優化和加速網絡建模過程。但是，與word2vec不同的是，DeepWalk用隨機游走獲取了網絡上節點的關系序列,所以Perozzi等認為隨機游走序列等同于語言模型中的句子。

文獻[4]證明DeepWalk算法本質是一種隱式的矩陣分解算法，其通過分解矩陣M=(A+A2)/2代替DeepWalk算法中被分解的矩陣Mij,即Mij是網絡隨機游走矩陣A組成的，A表示網絡隨機游走轉移概率矩陣，矩陣A的每個元素的物理意義是頂點vi和隨機游走到其他頂點vj的概率, 定義矩陣A的每一個元素為Aij=1/di，其中di是節點的度[4]。

有趣的是文獻[2]證明了word2vec中的SGNS框架是隱式矩陣分解SPPMI矩陣；文獻[4]證明了DeepWalk算法是在網絡表示中利用了word2vec中負采樣Skip-Gram框架(SGNS框架)， 而word2vec中的SGNS框架是被Levy等在文獻[2]中證明了隱式分解矩陣的框架，所以基于上述事實，顯然可以得出2個結論：

第1，由于自然語言處理的詞可以看作是復雜網絡表示學習網絡中的節點，所以在自然語言處理中基于詞向量的SGNS模型既可以訓練語言模型，也可以訓練網絡表示學習模型。

第2，SGNS框架在復雜網絡表示學習學科和自然語言處理的詞表示學習中都被證明是隱式的矩陣分解,只是SGNS框架分解的目標矩陣不同。詞表示學習中SGNS模型分解的是互信息SPPMI矩陣，其中SPPMI矩陣是表示詞和上下文之間關系的矩陣。網絡表示學習中SGNS分解的是隨機游走M矩陣,其中M矩陣是表示網絡隨機游走序列中節點之間關系的矩陣。

Perozzi等[2]在文獻中提到了網絡隨機游走序列等同語言中的句子(移位正定互信息)，他從以下2方面說明：(1)網絡節點無標度，大多數復雜網絡研究者認為無標度網絡節點具有冪律分布特性，即網絡中度大的節點比較少，度小的節點比較多；(2)語料中的單詞詞頻符合Zipf規律(冪律)，即語言中常用詞很少，很多詞不常被使用，并給出了2個數據實例：

第1個是YouTube網絡。YouTube是社交網絡，社交網絡是無標度網絡[2],無標度網絡的節點是符合冪律分布的；

第2個是維基百科的語料庫，并統計了語料庫中單詞出現的頻率，結果發現詞頻符合Zipf冪律規則。

但是，基于詞頻和節點頻率符合冪律從而證明隨機游走序列等同于句子是不充分的，原因有下面3點：

(1)僅從基于網絡節點度服從冪律與自然語言中詞頻服從冪律，就將網絡中隨機游走序列等同于自然語言中的句子[3]，理論上并沒有嚴格的證明，這樣的類比是牽強的；

(2)這種類比沒有比較實驗做支撐；

(3)到目前沒有其他文獻比較過2者是否等同。

那么，語言模型中分解SPPMI矩陣和網絡表示學習中分解的M矩陣是否存在等價關系？即句子是否等同隨機游走序列？本文旨在通過實驗驗證隨機游走序列和句子的等同性。

2 相關工作

本文用奇異值分解SVD(Singular Value Decomposition)方法[5 - 7]和誘導矩陣補全IMC(Inductive Matrix Completion)方法驗證句子和游走序列的等同性。

(1)用SVD方法分解SPPMI矩陣與M矩陣。

(2)用IMC方法也分解SPPMI矩陣與M矩陣。

基于以上2個對比實驗，本文從理論上基于自然語言處理方面和網絡表示學習方面的相關文獻，設計了2個實驗進行命題實證，如果網絡節點分類準確率幾乎相等或近似，則認為網絡隨機游走序列等同于句子。如果實驗結果差異較大，則2者不等同。這種等價可以作為自然語言表示學習和網絡表示學習的橋梁，也為學習潛在的表示時提供相互借鑒。

3 詞向量模型和隱式分解

3.1 word2vec模型

word2vec是自然語言處理中語言建模及語言特征學習的模型和技術。從語料庫中將單詞映射到實數空間的向量被稱為詞向量。word2vec用大文本語料作為其輸入，將語料庫上千萬維的單詞映射到幾百維的實數向量空間中。這樣語料庫中語義相近的單詞，其詞向量也會很接近。word2vec的SGNS模型目標函數[1]如式(1)所示。

(1)

(2)

其中,σ是激活函數，k是采樣率，W是詞矩陣，w為W中的詞向量,Wc是上下文矩陣,c是Wc樣本單詞的上下文向量，|D|是詞典大小，·是向量的點積。

3.2 word2vec隱式分解

對目標函數求導并極值優化，由互信息的概念:

得到

(3)

式(3)說明PMI是一對離散結果(詞和上下文)之間的信息理論關聯度量，PMI值取了詞和上下文共同出現的聯合概率與它們獨立出現的概率之間的比值的對數，計算PMI矩陣是挑戰性的工作，如果考慮一個單詞和這個詞的上下文沒有共同出現的概率(如考慮的詞是“數據”，“大數據會議”是數據的上下文)，則矩陣MPMI的行包含許多從未觀察到的詞對或者只出現1次的詞對，那么在語料庫中只出現1次的詞對(如“大數據會議”)，這樣做會導致PMI值為負，而對于未觀察到的1對單詞(如“數據結構”)，PMI值會出現PMI(w,c)=log 0=-∞的情況，這種情況下的PMI矩陣定義不明確，大的語料庫不僅密集且尺寸|VW|×|VC|很大，|VW|是詞矩陣的維數，|VC|是上下文矩陣的維數，文獻[2]將PMI構造為正定的PMI(PPMI)并取最大，得到：

PPMIk(w,c)=max(PMI(w,c),0)

(4)

利用移位的負采樣可以顯著改善由PMI矩陣得到的嵌入詞的表示向量，k為構造PMI值的采樣窗口值，所以如果設k>1，式(4)得到的矩陣將不包含任何無限值，從而使文檔中所有的單詞和上下文對被觀察到，這樣移位非負逐點互信息矩陣SPPMI為：

SPPMIk(w,c)=max(PMI(w,c),-logk,0)

(5)

4 網絡表示學習模型和隱式分解

4.1 DeepWalk模型目標函數

DeepWalk使用隨機游走來獲取網絡的結構，即假設網絡采樣是從網絡中任意一個節點隨機游走到另一個節點，DeepWalk算法是將網絡節點及上下文的關系映射到實數空間的算法，其中網絡節點在算法中表示為網絡節點的表示向量。如果網絡空間中節點彼此接近，則網絡節點向量也會很近似。DeepWalk的SGNS模型目標函數[4]為：

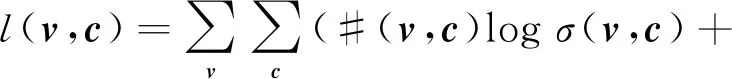
(6)

(7)

其中，σ是激活函數，k是采樣率，v是網絡節點的表示向量，c是網絡節點的上下文向量，|D|是節點集合的大小，·是向量的點積。可以看出式(7)與式(1)中word2vec的SGNS目標函數是一致的。

4.2 DeepWalk隱式分解

文獻[4]證明了DeepWalk本質上是對矩陣Mij的分解。作者將誘導矩陣補全的優化函數變換為式式(8)：

(8)

其中，矩陣A是隨機游走矩陣[8],t為隨機游走步數。

(9)

其中，Aij表示一步轉移矩陣的元素，(i,j)是從i到j點的邊，(i,j)∈E。

假設di是頂點i的度，隨機游走從節點i開始，ei表示頂點i的初始狀態，式(8)相當于[eiA]j，該項表示從頂點i的初始狀態走一步到頂點j的概率，[eiAt]j項表示頂點i從初始狀態恰好以t步游走到頂點j的概率，其中At是隨機游走概率矩陣，于是隨機游走的過程可用式(10)表示：

[ei(A+A2+…+At)]j

(10)

從式(10)發現，精確計算Mij矩陣，計算代價高，Yang等[4]用近似矩陣M代替Mij實現，如式(11)所示：

(11)

這樣的替代對網絡節點分類[9]的正確率影響不是很大，而且可以加快計算速度。

5 word2vec和DeepWalk的關系

實際上DeepWalk也可以使用word2vec的CBOW模型和Hierarchical Softmax優化方法，底層的模型如圖1所示。

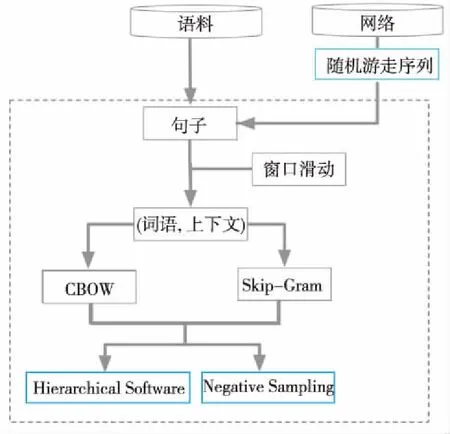
Figure 1 Model of word2vec and DeepWalk圖1 word2vec和DeepWalk的共同底層模型

窗口滑動用于詞或節點對采樣。word2vec的2個神經網絡模型CBOW和Skip-Gram實現訓練的思路是不一樣的，Skip-Gram神經網絡模型是根據當前詞出現的概率預測與它對應的上下文詞語概率的模型。CBOW神經網絡模型是一種根據上下文詞語預測當前詞語出現的概率的模型。Hierarchical Softmax優化方法是詞向量訓練時將神經網絡的輸出Softmax層的概率計算，用一棵霍夫曼樹替代，那么Softmax概率計算只需要沿著樹形結構進行統計訓練。在霍夫曼樹中，隱藏層到輸出層的Softmax映射不是直接一步完成的，而是沿著霍夫曼樹一步一步完成的，因此這種Softmax取名為Hierarchical Softmax。使用霍夫曼樹編碼方法，既可以提高模型訓練的效率，也可以減少詞向量存儲空間。但是，如果訓練樣本里的中心詞w是一個很生僻的詞，那么會使得霍夫曼樹的訓練時間變得很長。于是Negative Sampling優化方法摒棄了霍夫曼樹，采用了負采樣的方法來加速詞向量訓練。

而文獻[3]中證明了word2vec中的SGNS相當于分解SPPMI矩陣，文獻[4]中證明了DeepWalk中的SGNS相當于分解M矩陣，在網絡表示學習中,DeepWalk算法采用了Skip-Gram模型和 Negative Sampling優化方法,它是自然語言處理word2vec詞向量里的模型用在網絡表示學習DeepWalk算法里了，所以也可以使用word2vec模型中訓練模型和優化方法的其他組合。工程和研究人員可以根據不同目的去選擇訓練模型和優化方法。

6 句子和隨機游走等同的實例證明

本文設計了2個實驗，實驗流程如圖2所示。

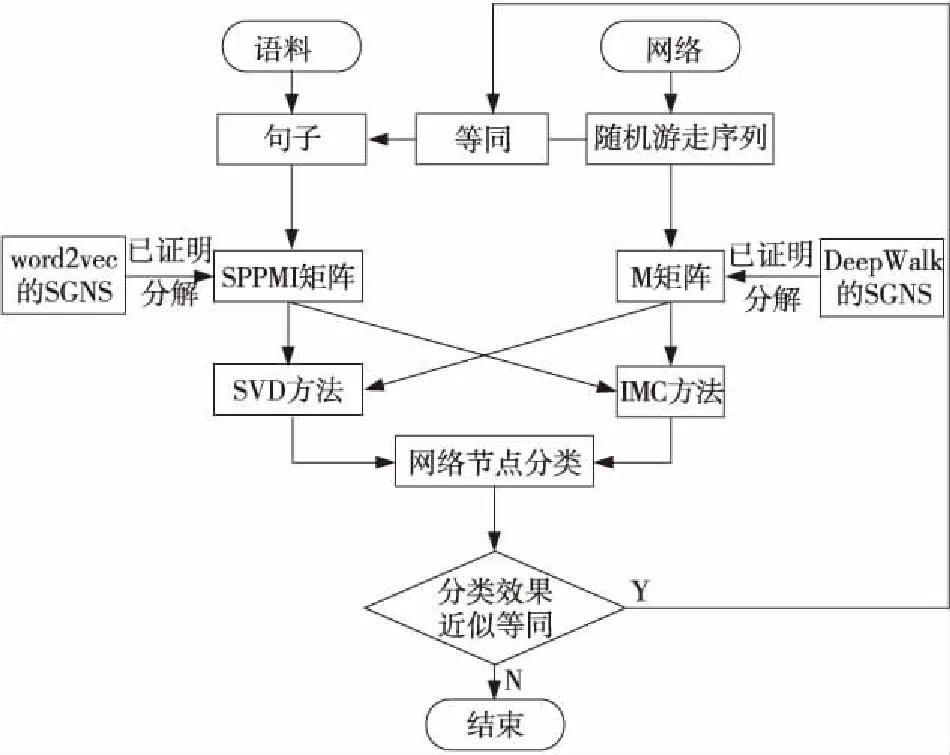
Figure 2 Flow chart of comparative experiment圖2 對比實驗流程圖

文獻[3]和文獻[4]都用到了矩陣的隱式分解，但是它們使用的矩陣分解方法是不同的，1種方法是奇異值分解(SVD)，另1種方法是誘導矩陣補全(IMC)[10]。

第1種方法：奇異值分解SVD。文獻[3]使用SVD將SPPMI矩陣分解如下：

MSPPMI=U·Σ·VT?

(12)

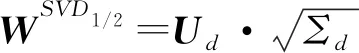
第2種方法：誘導矩陣補全(IMC)[10,12],它使用了基因特征輔助矩陣X∈Rd1×m和疾病特征輔助矩陣Y∈Rd2×m分解基因-疾病目標矩陣M∈Rm×n，它的優化目標函數如式(13)所示：

(13)

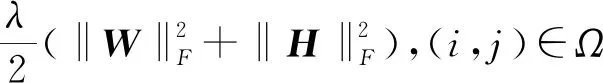
文獻[12]中利用了誘導矩陣補全(IMC)算法，將文本信息加入到誘導矩陣中，文獻[4]用簡化的矩陣M代替了DeepWalk算法中的矩陣Mij,從而得到了準確率更高的網絡節點表示向量，他的算法名為TADW(Text-Associated DeepWalk)，TADW算法相當于IMC方法分解隨機游走矩陣。而采用誘導矩陣補全，可將網絡節點的文本屬性構造成文本特征矩陣，讓網絡結構學習包含更多的網絡節點信息[12]，使分類任務準確率更高。本文基于TADW算法進行了改進，用誘導矩陣補全對SPPMI矩陣進行分解，并與分解M矩陣[13 - 18]進行對比。

7 實驗與結果

本文設計了2個實驗用于驗證本文的命題：

(1)用SVD分解SPPMI矩陣和網絡隨機游走構造M矩陣，并在數據集上進行網絡節點分類性能測試。

(2)用IMC方法分解矩陣W和H，具體實現時本文針對文獻[12]進行改進，用誘導矩陣補全方法對M矩陣和SPPMI矩陣分解(本文將改進對比的算法標為STADW)，并在數據集上進行網絡節點分類性能測試。

實驗設置：對于3個社交網絡的數據集Citeseer，Cora和Wiki[16 - 18]，實驗設置的參數為：表示向量維數為128，數據集的數據訓練比例是10%,30%,50%,70%,90%，負采樣率為5。實驗結果如表1～表3所示。表中的M和SPPMI分別代表只分解M和SPPMI矩陣后分類算法。

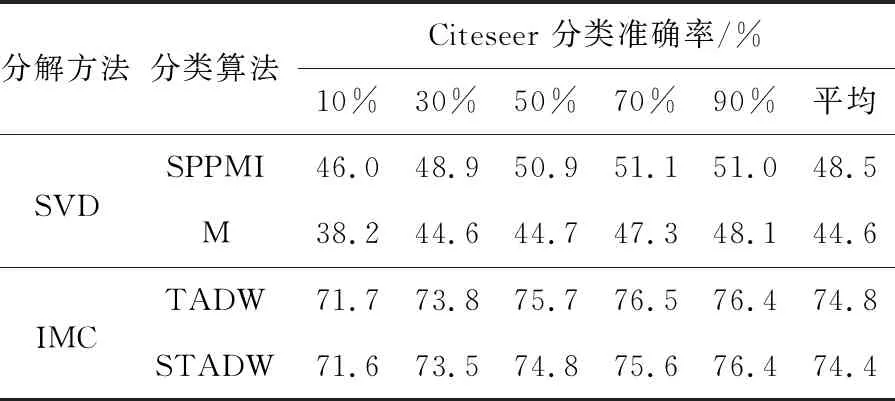
Table 1 Classification experiment by various methods on Citeseer data set表1 數據集Citeseer上各種方法分類實驗

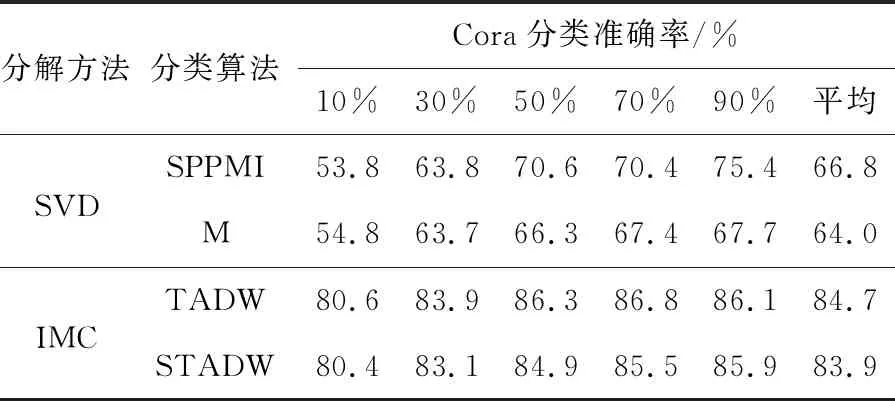
Table 2 Classification experiment by various methods on Cora data set 表2 數據集Cora上各種方法分類實驗

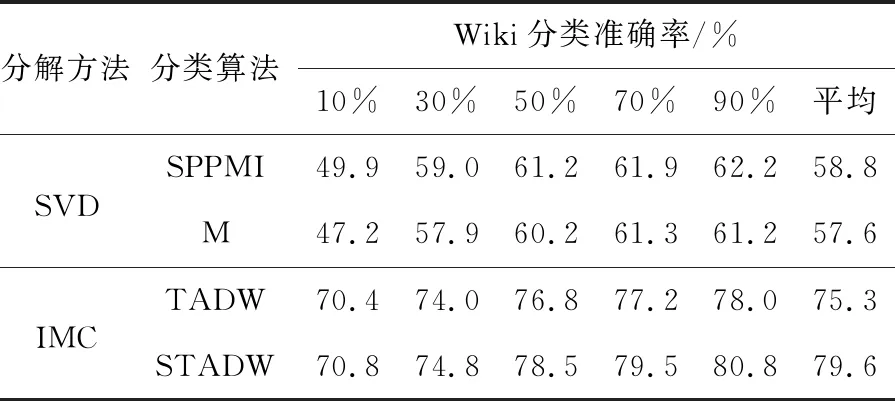
Table 3 Classification experiment by various methods on Wiki data set 表3 數據集Wiki上各種方法分類實驗

對比實驗是在3個公開的社交網絡數據集上進行的，數據集的類別已分好，對比實驗為奇異值分解(SVD)和誘導矩陣補全(IMC)2種方法對社交網絡數據集的網絡節點的進行分類。使用的3個數據集為Citeseer，Cora和Wiki。 其中引文數據集Citeseer是有6個類別的3 312種出版物，共有4 732條邊的數據集; 引文數據集Cora集有7個類別的2 708篇機器學習論文，共有5 429條鏈接的邊。Wiki數據集包含來自19個類2 405篇文檔共有17 981條邊。

比較表1～表3的數據，可以看出在3個數據集上,奇異值分解SVD方法的2行數據相差0.01，在誘導矩陣補全方法上，TADW 和STADW的2行數據相差0.03。

本文還研究了不同向量維數的IMC方法和SVD方法網絡節點分類的正確性，如圖3～圖5所示。

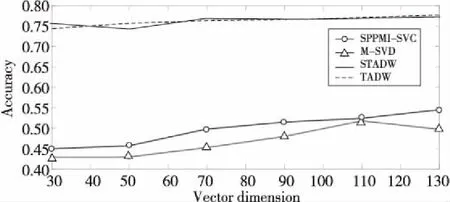
Figure 3 Comparison of classification accuracy on Citeseer data set圖3 數據集Citeseer上分類準確率對比

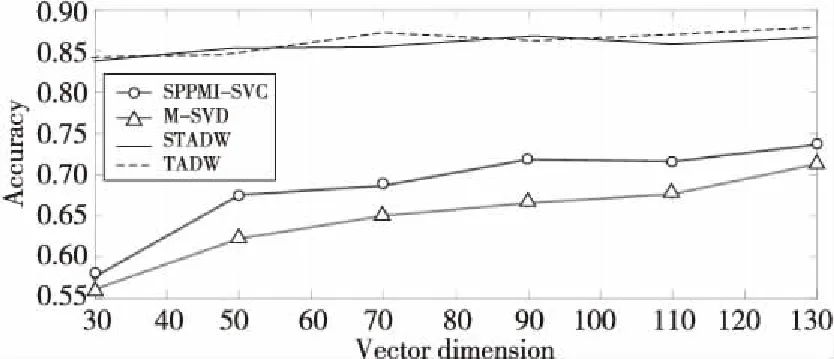
Figure 4 Comparison of classification accuracy on Cora data set圖4 數據集Cora上分類準確率對比

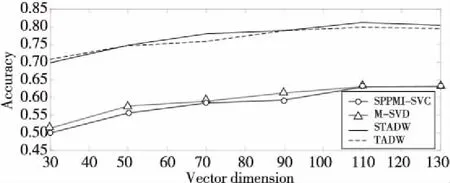
Figure 5 Comparison of classification accuracy on Wiki data set圖5 數據集Wiki上分類準確率對比

圖3～圖5 分別表示在3個數據集上用2種方法(SVD和IMC)分解M矩陣和SPPMI矩陣的結果。實驗設置為：表示向量維數為30,50,70,90,110和130，需要注意的是，在TADW與STADW算法中學習得到的網絡表示向量維數需要在上述表示向量維數上乘以2，為了直觀表示，在圖3～圖5中對這2種算法并沒有乘以2，實驗數據集的數據訓練比例取0.9，負采樣率k為5。

從圖5～圖7可知，SVD方法和IMC方法準確率差距浮動值為1%，一般的準確率差距浮動值不超過5%，準確率是可信的，直觀地從圖3～圖5的上半部分的實線和虛線及圖3～圖5的下半部分的帶圈線和帶三角形線可觀察到。

實驗用2種方法(即SVD和IMC)對M矩陣和SPPMI矩陣分解，并在不同的表示向量的維數下研究句子和隨機游走的等同性，從表1～表3和圖3～圖5都能明顯觀察出隨機游走和句子等同，證明了本文提出的命題。

8 結束語

本文在對詞表示學習[19 - 22]和網絡表示學習理論研究基礎上，發現它們可以采用相同的SGNS模型。而 SGNS模型在詞表示學習[22 - 30]領域和網絡表示學習領域都已經被證明是隱式地分解目標特征矩陣，只是在這2個領域中分解的目標特征矩陣不同，即詞表示學習中SGNS模型分解的是SPPMI矩陣，分解SPPMI矩陣相當于神經網絡建模語句中詞語之間關系的過程，網絡表示學習中SGNS分解的是M矩陣,相當于神經網絡建模網絡隨機游走序列中節點之間關系的過程，但是對分解的目標特征矩陣沒有研究結果。為此，本文提出了一種新的證明方法，通過設計2個對比實驗，分別在3個公開的網絡數據集上做節點分類任務，實驗結果證明了句子和隨機游走序列的等同性。實驗涉及網絡表示學習和自然語言處理2個學科，為更深層次地理解語言本質和網絡表示學習的本質研究提供了實驗依據。