基于二次型規劃函數的無功補償優化方法

林 霞，宋慧杰，陳三波

（1.國網山西省電力公司，山西 太原 030021；2.萬家寨水務控股集團有限公司，山西 太原030012；3.中國能源建設集團山西省電力勘測設計院有限公司，山西 太原 030013）

0 引 言

隨著國民經濟的快速增長，全社會用電負荷隨之增加，需要不斷加大電網建設投資以滿足快速增長的負荷需求。電網企業不僅要為用電企業提供可靠的電能供應，還需確保其自身電網的安全經濟運行，提高電能的利用和轉換效率，避免電網建設的投資浪費。隨著電力體制改革的日益深化，電網運行的經濟性成為電網建設的決定因素之一。合理配置無功補償裝置是電力系統經濟運行、減少電能損耗以及提高電網輸送效能的重要手段，對提高用戶用電質量和提高電網企業的經濟效益具有重大意義。

提高電壓水平及電能質量的重要手段之一，是在相關站點的主變低壓側配置一定容量的無功補償裝置。該裝置實際運行時根據電壓水平的高低決定分組投切的容量。但是，目前無功容量的配置原則主要通過長期運行經驗和粗略計算，缺乏一定的理論支撐。配置過少，造成電壓水平過低、設備出力不足、損壞、損耗增加等問題；配置過剩，造成投資浪費，無功補償裝置的投資不能獲得最佳回報。無功優化計算正是解決上述問題的重要手段，通過優化計算合理配置無功補償裝置，最大限度地優化無功潮流分布，提高電壓水平和電能質量。無功優化問題難點主要集中在無功優化模型的建立和無功優化問題求解方法的研究。現階段電網系統愈加龐大和復雜，對無功優化問題的建模及求解方法提出了更高的要求[1]。

1 無功功率的補償及優化

1.1 無功的補償方式

常見的低壓補償方式包括樞紐站集中補償、配電網分散補償以及用戶終端就地補償。針對城市低壓配電網，采用的補償方式是分散補償。分散補償是根據電力系統及用戶的需要，按照局部負荷大小配置無功補償容量，通常是在公用變壓器上安裝電容器組進行無功補償。通過分散加裝補償裝置的方法，可以改善電網系統無功潮流分布，從而進一步改進設備的承載能力，提高電壓質量，降低網絡損耗，是目前經濟可行的補償措施，體現了無功“分散補償，就地平衡”的原則。

1.2 無功的優化方法

在電力系統無功優化領域，常規優化方法主要有非線性規劃法、線性規劃法以及混合整數規劃法等。非線性規劃法是最先被應用到電力系統無功優化的方法之一，其中具有代表性的有簡化梯度法、牛頓法最優潮流算法以及二次規劃法。二次規劃法是發展較為成熟的一個分支。因無功優化中的目標函數和約束條件常常是二次函數的形式，故二次規劃法常用于無功優化的求解。本文采用基于MATLAB的二次規劃函數。

二次規劃的標準形式為：

式中，H是m×m階矩陣；A是n×m階矩陣；Aeq是n×m階矩陣；x,f,lb,ub∈Rm；b,beq∈Rn。

MATLAB優化工具箱中二次型規劃函數的用法：

返回一組具有上下限、滿足不等式約束及等式約束，且使函數f(x)最小的向量x以及f(x)的最小值fval[2]。

2 無功優化的數學模型

通常把無功優化表示成含有約束條件的非線性數學模型。目標函數可以有多種選擇形式，如以線損最小、年運行費用最小、年支出費用最小以及年經濟效益最高為優化目標。本文采用年經濟效益最高為目標函數：

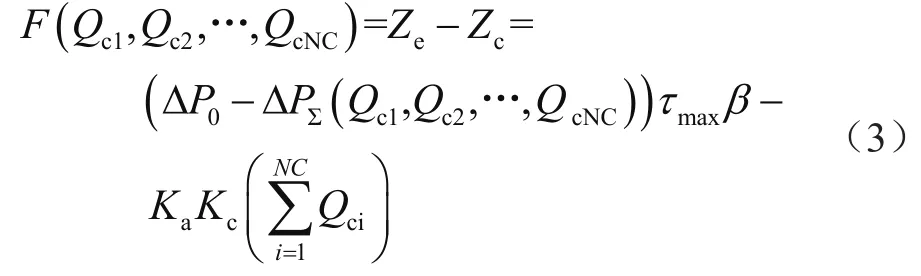
式中，Qc1,Qc2,…,QcNC為NC個無功補償點的補償容量；Ze為投入補償電容之后年節約電能費用，單位為元；Zc為新裝電容器的年綜合造價，單位為元；ΔP0為補償前最大負荷下的有功損耗，單位為kW；ΔPΣ(Qc1,Qc2,…,QcNC)為補償后最大負荷下的有功損耗，單位為kW；τmax為最大負荷損耗小時數；β為有功電價，單位為元/（kW·h）；Ka為補償裝置的維護折舊率；Kc為安裝單位補償容量的綜合投資，單位為元/kvar。本文考慮的約束條件是支路功率因數約束和節點電壓約束：

式中，l=1,2,…,NF，NF≤NL，NL為系統總支路數；NF為功率因數約束支路數；k=1,2,…,KV，KV≤N，N為系統總節點數，KV為電壓約束節點數。VK為K節點的電壓值，cosφl為l支路的功率因數。

因無功補償而減少的年電能損耗費用若大于投資安裝無功補償設備的年綜合造價，即節省的費用超過投資的費用，則認為是劃算的，其差值為年經濟效益，優化目的是年經濟效益最大。

二次型規劃函數quadprog()所得到的目標函數的最優解是最小值，本文采用的目標函數（年經濟效益）的優化目的是最大值，因此對目標函數進行如下變形（即等式兩邊同取負值）：

進而將目標函數年經濟效益最大轉換成求目標函數FT的最小值。

式（5）中的第3項根據潮流計算得到。本文采用的潮流計算方法引入一個節點-支路關聯矩陣（不考慮源點），通過求得這個矩陣，根據已知的節點負荷求出支路功率，拓撲結構如圖1所示。

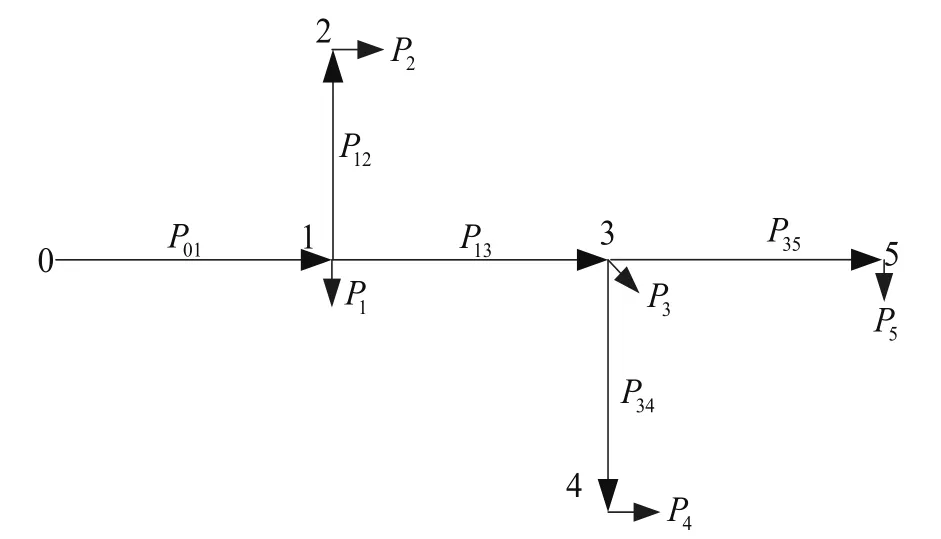
圖1 拓撲結構圖

圖1中，數字0～5是節點編號，數字0是源點；P01～P35是各支路功率（待求量，下標數字順序代表功率流向）；P1～P5是各節點功率（已知量，如果不是負荷節點，則為零）。因此，圖1的節點-支路關聯矩陣為：

矩陣中，1代表注入功率，-1代表流出功率。現在考慮式（5）的第1項和第2項，那么新的目標函數可以寫成：

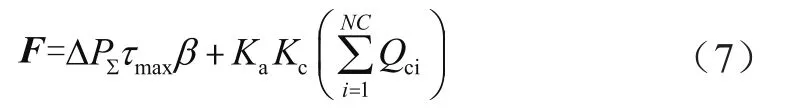
式中，ΔPΣ是補償前最大負荷下的有功損耗，具體表達式為：

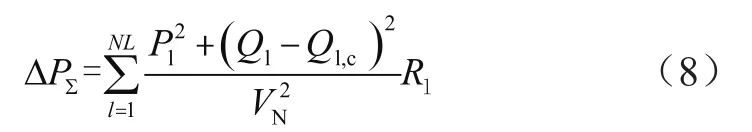
式中，P1、Q1為無功補償之前各支路的有功、無功功率；R1為各支路的電阻；VN為線路額定電壓；Q1,c為線路l下游節點電容器補償容量之和，具體表達式為：

式中，α1,ci為0或1的變量。α1,ci=1表示線路l下游節點集合中含有電容器ci，α1,ci=0表示線路l下游節點集合中不含電容器ci。

本文算法只考慮了支路功率因數約束和節點電壓約束，具體描述為：

式中，Vs為電源點電壓；βk,1為0或1的變量。βk,1=1表示電壓約束點k的電壓與支路i的壓降有關，βk,1=0表示電壓約束點k的電壓與支路i的壓降無關，Rl為支路的電阻，Xl為支路的電抗。

結合式（7）～式（10）可知，無功補償容量的優化的目標函數和約束條件可描述為：

求出支路功率和α1,ci、βk,1后，式（11）中的變量就只有Q1,ci。

本文借助MATLAB優化工具箱的二次型規劃函數進行仿真計算，應將目標函數及其約束條件轉換成如式（3）所示的二次型規劃函數所要求的標準形式進行計算。

經過公式推導得到目標函數及約束條件的標準形式如下：

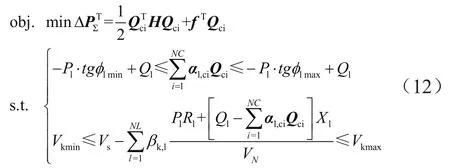
式中，Qci是各無功補償點補償電容組成的NC維列向量；QciT為Qci的轉置；H是NC×NC階矩陣，具體表達式為：

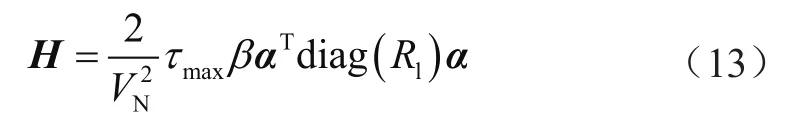
式中，α是NC×NC階矩陣；diag(R1)是NL×NL階矩陣，矩陣內元素為各支路電阻組成的對角矩陣。可以看出，目標函數是一個標準的二次型函數。

以上分析為后續的優化計算做好了準備。下面通過一個實際算例來驗證數學模型和算法的有效性。

3 實際系統分析

如圖2所示，某地區城市配電網共24個節點，節點1為電源點，額定電壓110 kV，24條支路，規劃的無功補償節點有15個。目標函數為該地區局部配電網年經濟效益，優化目的是經濟效益最高，以無功補償設備容量作為可調變量進行優化計算。

圖2 某地區城市局部配網示意圖

選取部分節點作為補償點，采用本文的數學模型及算法計算各補償點的無功補償容量。經過計算可知，補償無功后，年電能損耗費用較未補償無功之前減少了50萬元，大于無功補償設備的投資費用，即節省的費用超過了投資的費用。補償無功后，各節點的電壓質量得到了改善，補償前后節點電壓結果如表1所示。

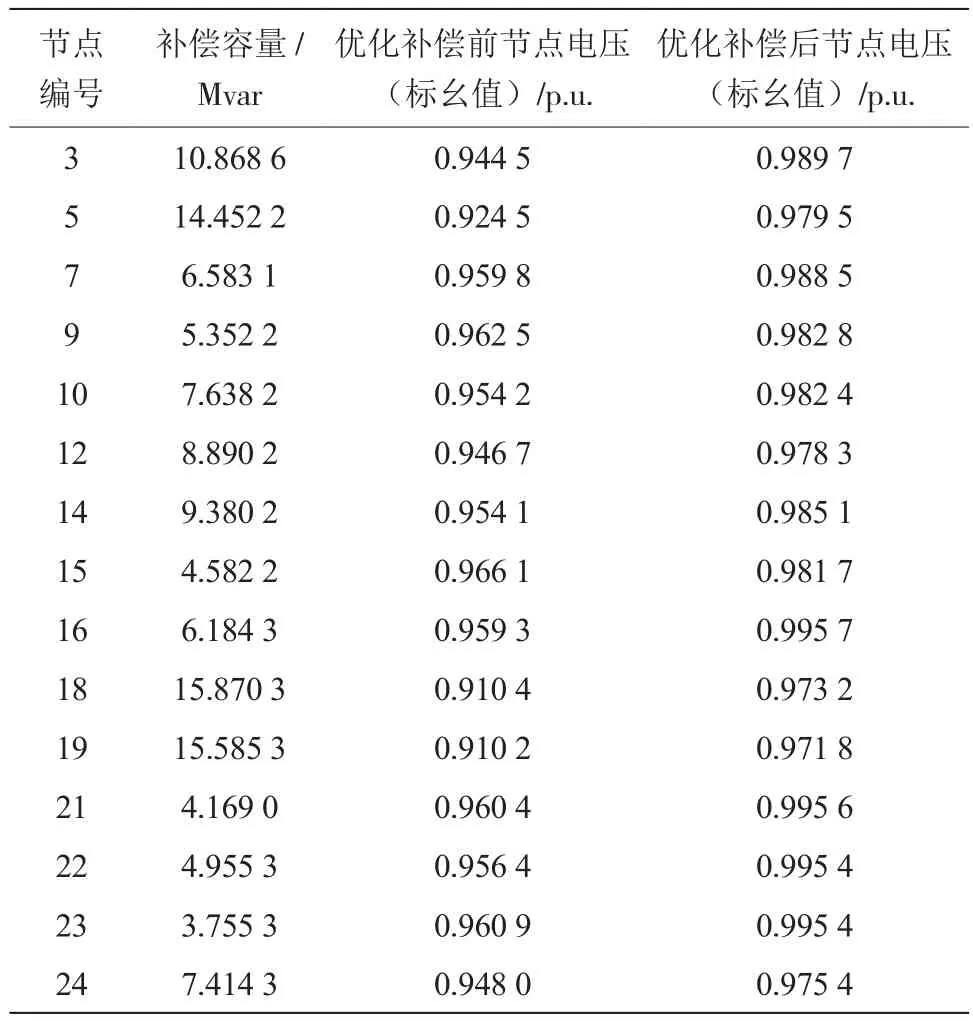
表1 部分節點最優無功補償容量及電壓優化結果

4 結 論

采用上述方法安裝的無功補償裝置能夠降低網損，提高電壓質量，且投資少，經濟效益明顯。通過實際算例證明，優化模型及算法具有合理性，二次型規劃算法是有效的。