求解半線性特征值問題的搜索延拓法

謝資清

（湖南師范大學 數學與統計學院 計算與隨機數學教育部重點實驗室，湖南 長沙410081）

考慮如下半線性特征值問題

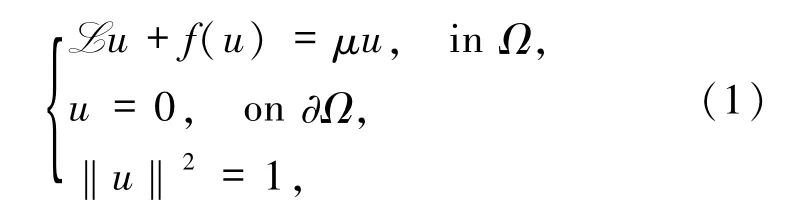
其中，L是一致橢圓算子，Ω?Rd是一個光滑有界區域，‖·‖為L2（Ω）范數，f是一個光滑非線性函數且滿足f（0）=0.

模型問題（1）廣泛出現在現代科學的各個領域，例如：激光傳輸［1］、電子結構計算［2］、玻色-愛因斯坦凝聚（BEC）［3］等.近年來，人們對模型問題（1）的一個主要研究興趣是設計計算最小能量特征態（基態）的數值方法和建立相關理論［4-8］.隨著科學技術的發展，具有更高能量的特征態（激發態）越來越受到科學家們關注.Bao 等［9］對一些用于刻畫BEC的半線性薛定諤特征值問題，使用Hermite 函數構造好的初值，從數值上模擬了問題的基態和幾種激發態.Chang 等［10］設計了計算BEC 能級的自適應同倫算法，能有效計算BEC 的不同能級及相應的定態解.此外，Zhou 等［11-12］將他們提出的計算非線性方程多解的局部極小極大方法推廣到一類非線性特征值問題，計算了多個特征對，并建立了相關理論.

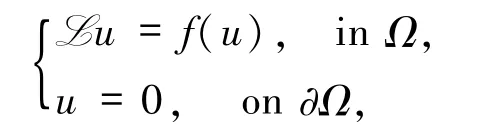
由于SEM簡單、高效的優勢，本文對原有SEM進行改進，使其適用于求解半線性特征值問題（1）.為此，首先在由線性算子L 的少數幾個特征函數張成的子空間中逼近模型問題，得到小規模非線性代數特征值問題，求解該問題獲得模型問題特征對的多個初值；然后，采用L 的更多的特征函數，進一步逼近模型問題的特征對以得到更好的初值；再用合適的數值方法離散模型問題，得到相對大規模的非線性代數方程組（非線性代數特征值問題）；最后用數值延拓法求解此非線性代數方程組，得到每個初值對應的特征對.為提高計算效率，本為將提出一種插值系數Legendre -Galerkin 譜方法用于離散模型問題（1）.

本文結構安排如下：第1 節給出求解模型問題（1）的SEM 的算法步驟和二維情形的插值系數Legendre-Galerkin譜離散格式；第2 節給出求解模型問題（1）的SEM 算法步驟和二維情形的插值系數Legendre-Galerkin 譜離散格式；第3 節應用改進的SEM 求解一類立方非線性特征值問題，給出計算實現的細節，并展示和分析數值結果.

1 求解半線性特征值問題的搜索延拓法

不失一般性，以下考慮L = -Δ的情形，則模型問題（1）的弱形式為：求（u，μ）∈（Ω）×R使其中（·，·）表示L2（Ω）內積，A（u，v）：=（▽u，▽v）.

1.1 SEM算法步驟基于原始SEM的思想，求解半線性特征值問題（1）的SEM 依次在3 層子空間Sk?Sn?SN上逼近模型問題，分為以下4 個步驟：

第一步 計算線性算子-Δ的特征對眾所周知，線性特征值問題

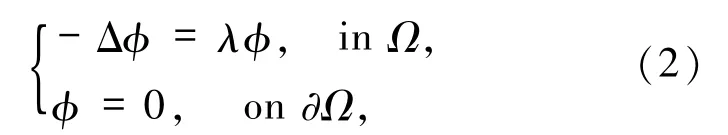
有可數無限多特征值：

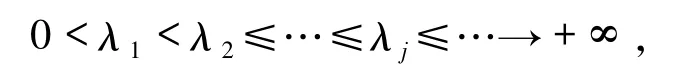
第二步 在較小的子空間Sk中逼近模型問題以獲得特征對的多個初值.

定義Sk=span｛φnj：1≤j≤k｝，其中nj為互不相同的正整數.求（uk，μk）∈Sk×R使

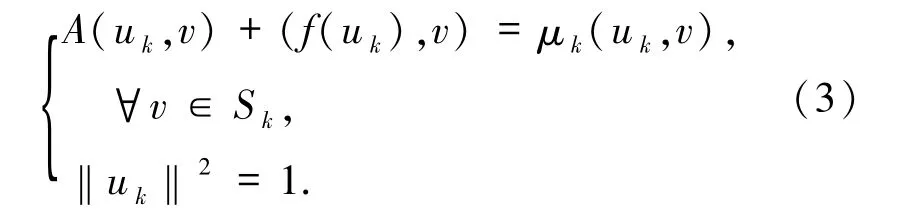
注意到

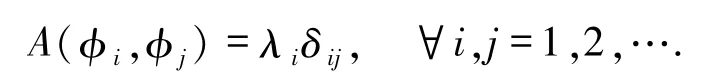
在（3）式中，令

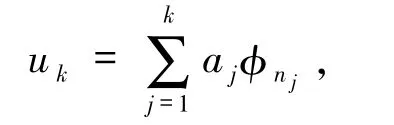
并取v=φni，i=1，2，…，k，得到關于k+1 個未知數（a1，…，ak，μk）的非線性代數方程組

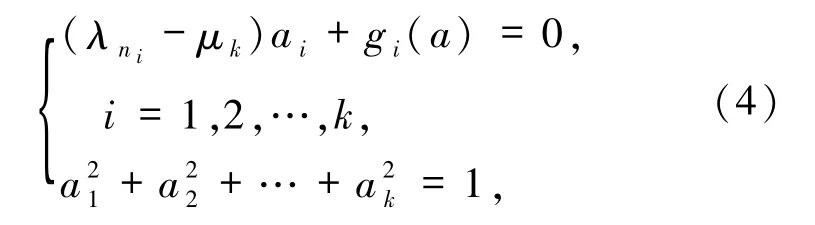
其中a=（a1，a2，…，ak），

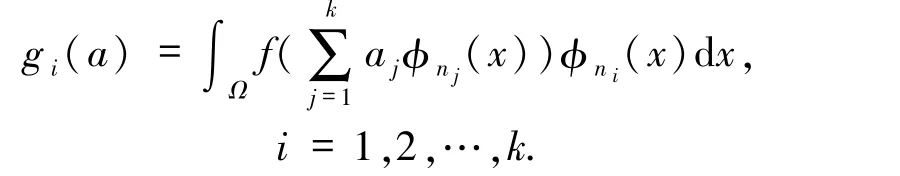
因為k較小，可通過解析方法或牛頓法等求得非線性方程組（4）的多解.特別地，當f 為多項式函數時，可利用數值代數幾何方法［19］得到（4）式的所有解.顯然，每組解）對應模型問題（1）的特征對的一個初值

第三步 在較大子空間Sn中進一步逼近模型問題的特征對以得到更好的初值.

為進一步逼近模型問題的特征對，取一個適當大的子空間Sn使Sk?Sn.設

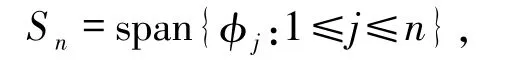
求（un，μn）∈Sn×R使

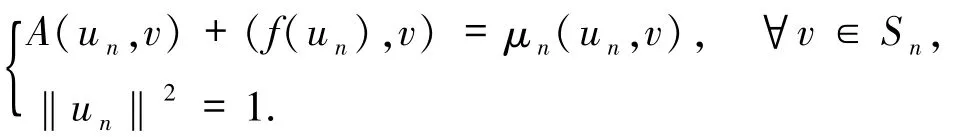
類似于第二步的討論，記

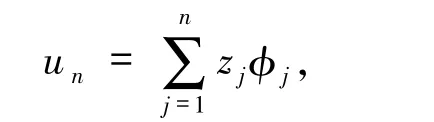
得到關于z=（z1，…，zn，μn）T∈Rn+1的非線性代數方程組

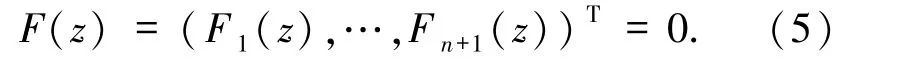
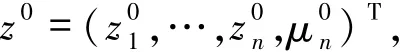
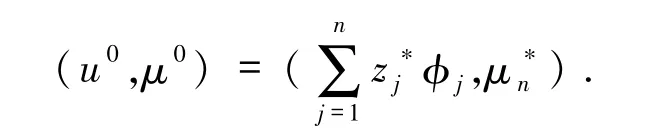
第四步 在大子空間SN中用合適數值方法離散模型問題并求解相應的非線性代數方程組得到最終數值解.

在SN中使用有限元、插值系數有限元或譜方法等離散模型問題（1），并用第二步或第三步得到的每個逼近解（u0，μ0）為初值，采用數值延拓法求解相應的非線性代數方程組，得到最終的數值解（uN，μN）∈SN×R.

由于第三步和第四步都涉及用數值延拓法求解非線性代數方程組，以方程組（5）為例介紹一類典型的牛頓型數值延拓法［15］.記J（z）為F（z）的雅可比矩陣.令G（z）= J（z0）（z - z0）.構造凸同倫函數

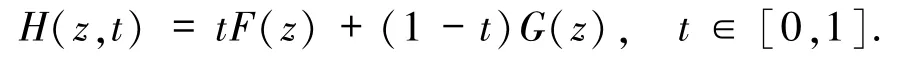
顯然，H（z0，0）=0.選取適當大的正整數m 和剖分0 =t0＜t1＜t2＜…＜tm=1.考慮子問題

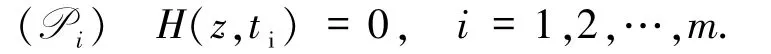
給定精度0 ＜ε?ε1?1.求解非線性代數方程組（5）的牛頓型數值延拓法的步驟如下：

1）依次對i=1，2，…，m -1，以zi，0=zi-1為初值，用如下牛頓迭代求解子問題（Pi）

zi，k+1= zi，k-（Ji，k）-1H（zi，k，ti）， k = 0，1，…，其中Ji，k=Hz′（zi，k，ti）=tiJ（zi，k）+（1 -ti）J（z0），直 到 條 件｜zi，k+1- zi，k｜ ＜ε1成 立，得 近 似 解

zi：=zi，k+1.

當｜zk+1-zk｜＜ε，得問題（5）的近似解z*：=zk+1.

1.2 插值系數Legendre-Galerkin譜離散由于譜方法具有高精度的優點，受插值系數有限元方法［1，16］的啟發，本文提出一種插值系數Legendre -Galerkin譜方法用于離散半線性特征值問題（1）.下面給出二維情形的離散格式，三維和更高維情形可類似得到.

為簡單起見，假設Ω =（-1，1）2.給定適當大的正整數N，考慮多項式逼近空間

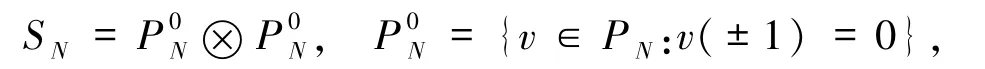
其中PN為定義在I =［-1，1］上且次數不超過N的多項式的全體.令為對應于Legendre -Gauss-Lobatto（LGL）點的拉格朗日多項式基（節點基），則二維張量形式的LGL 點和相應的節點基分別為

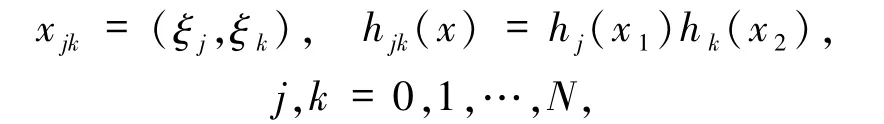
提出如下插值系數Legendre - Galerkin 譜方法：求（uN，μN）∈SN×R使

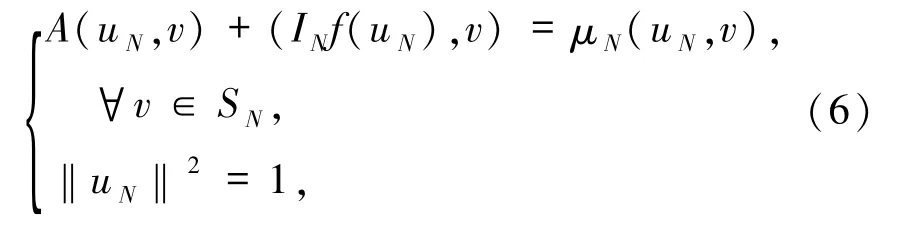
其中IN：C（ˉΩ）→PN?PN是基于二維LGL 點的拉格朗日插值算子，滿足：

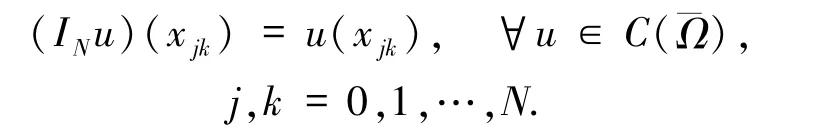
注意，（6）式中的INf（uN）是對f（uN）作整體插值.這是（6）式與標準Legendre -Galerkin 譜方法的重要區別.

注意到f（0）=0，有

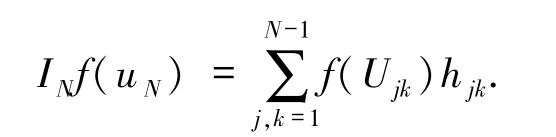
因為uN∈SN，所以

代入（6）式，并取vN=hlm，l，m =1，2，…，q =N -1，得到如下矩陣形式的非線性代數方程組

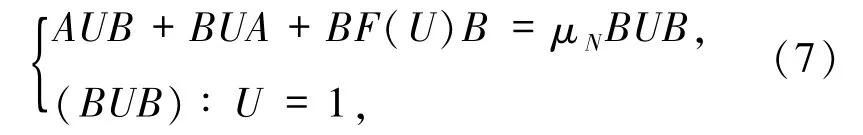
其中“∶”表示矩陣的Frobenius內積，定義為

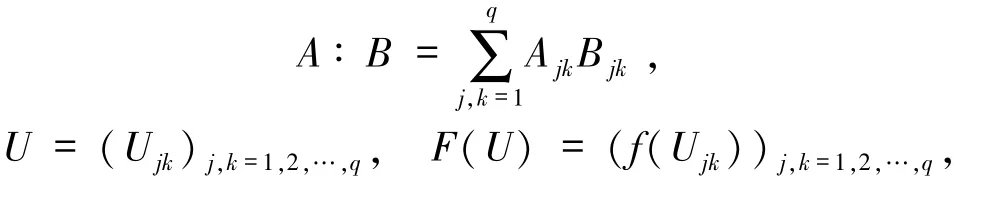
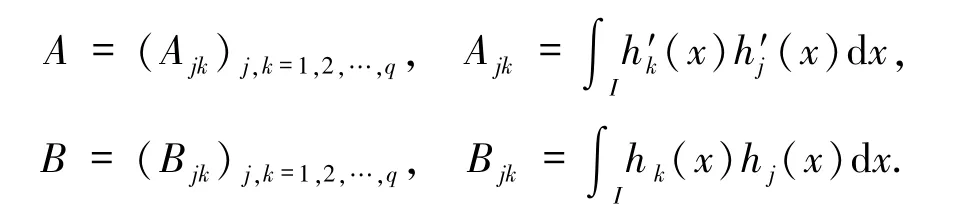
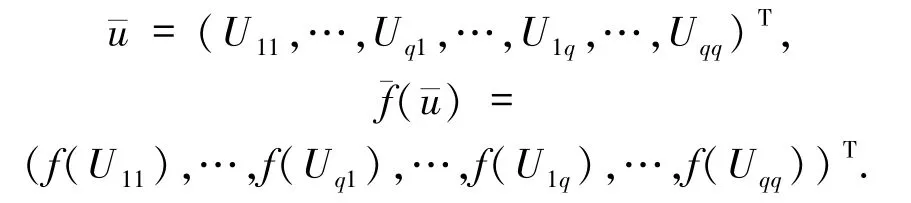
記K=B?A+A?B，M=B?B，其中“?”表示Kronecker乘積算子，定義為則方程組（7）可重寫為

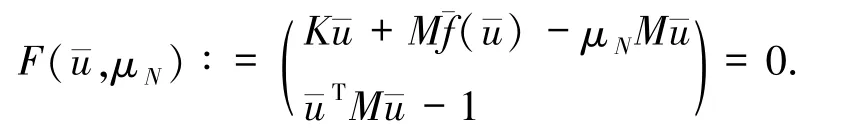
容易得出F的雅可比矩陣J為

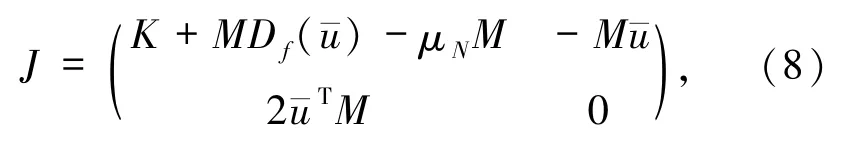
其中

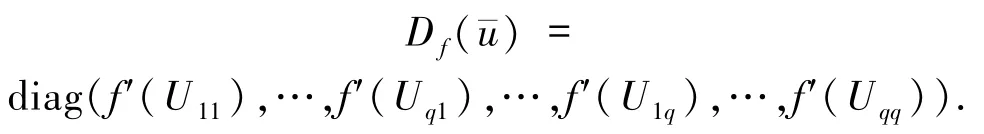
由此可見，插值系數法的運用，使得雅可比矩陣的表達式（8）比標準Galerkin譜方法簡單.事實上，由于K、M是常數矩陣，每步牛頓迭代中，更新雅可比矩陣的主要工作量僅是計算對角矩陣Df（ˉu）.這是插值系數法的主要優點.

2 一類立方非線性特征值問題的計算

取f（u）=u3，Ω=（0，π）2，考慮半線性特征值問題

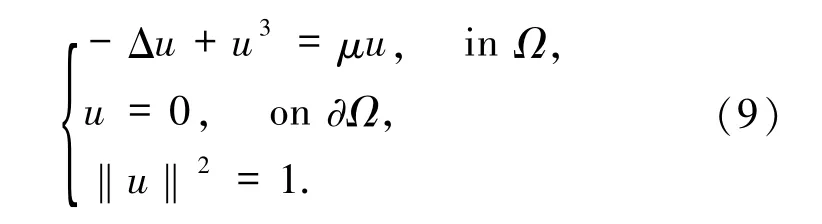
下面應用第2 節描述的SEM 求（9）式的多特征對（u，μ）.

首先，在SEM的第一步，直接計算得線性特征問題

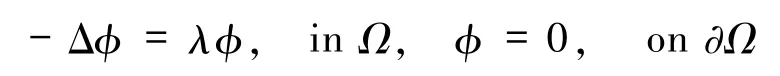
的特征值和相應的規范正交特征函數分別為

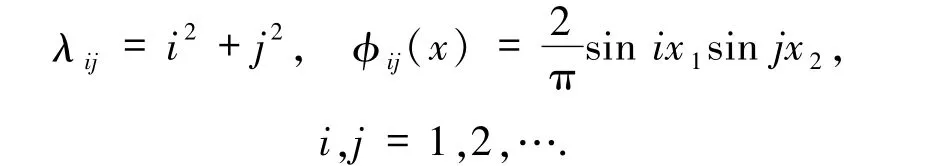
在第二步，考慮Sk是由-Δ的對應同一特征值λ的特征函數張成的子空間.設λ 是k 重特征值，則存在k個不同的正整數對（ip，jp）∈N+×N+使得

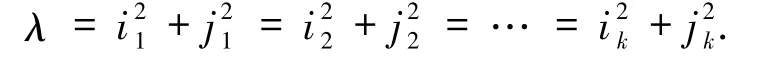
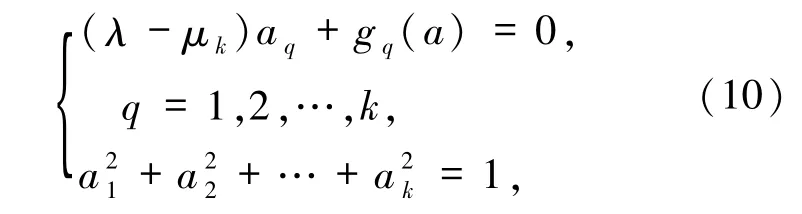
其中a=（a1，a2，…，ak），

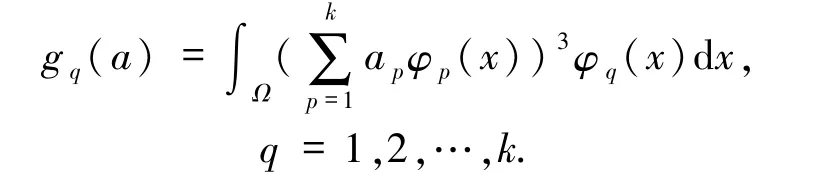
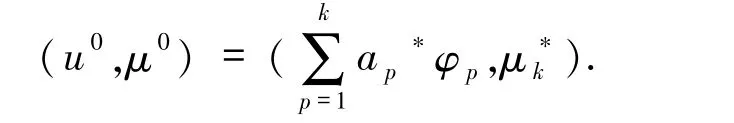
定理2.1非線性代數方程組（10）至少有3k-1 個解.

證明設（ip，jp）∈N+×N+滿足

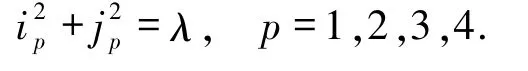
考慮積分

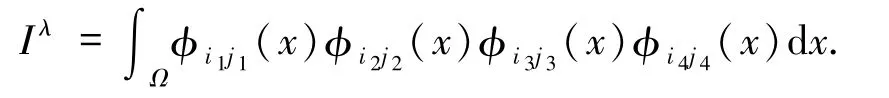
直接計算可知［15，20］：

i）若（i1，j1）=（i2，j2）=（i3，j3）=（i4，j4），Iλ=9/（4π2）；

ii）若有且僅有2 對（ip，jp）分別相等，Iλ=1/π2；

iii）其他情形，Iλ=0.于是

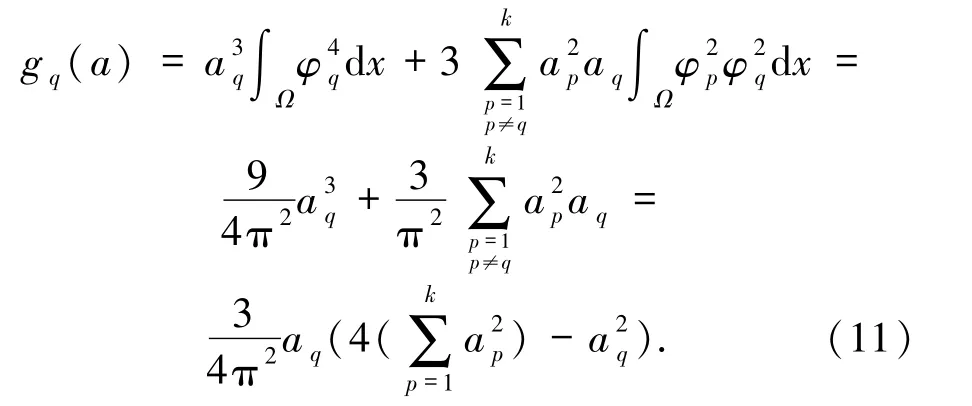
將（11）式代入（10）式得

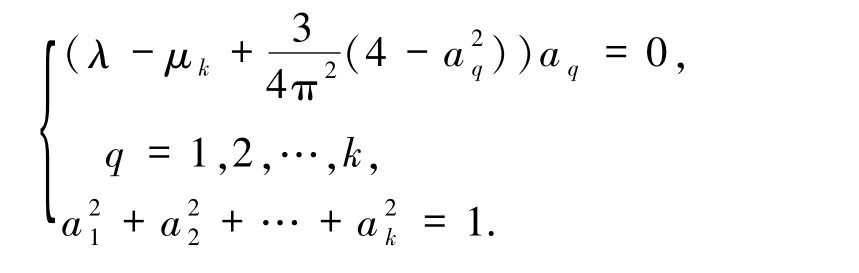
設r是向量a=（a1，a2，…，ak）的非零分量個數，顯然1≤r≤k.不妨假設，i =1，2，…，r，，可以得到解

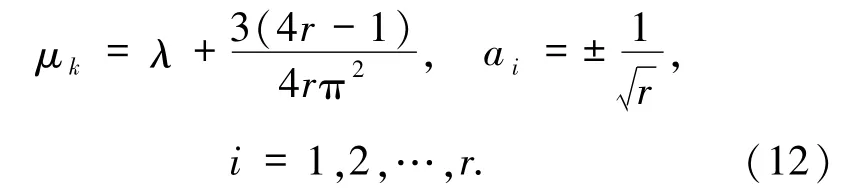
下面分別對k =1，2，3，4 情形，考慮Sk由-Δ的k重特征值對應的特征函數張成，給出相應的數值結果.在數值計算中，算法第三步的Sn通常由5～20 個基函數張成.在第四步，取N =32 進行離散.數值延拓法子問題個數取為10、牛頓迭代的精度控制數取為以下特征函數的圖像均在一個64 ×64 網格上呈現.

由此得到2 個（9）式的特征對數值解.圖1 給出了i=1，2，3 情形得到的（9）的特征函數uii的圖像，相應的特征值和初值信息列于表1.

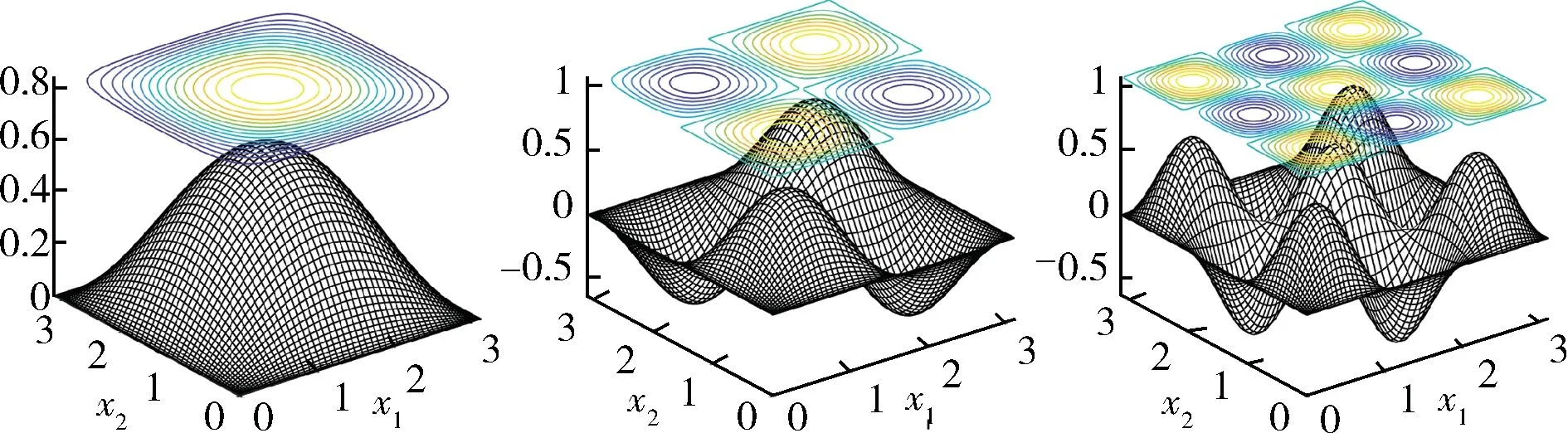
圖1 特征函數u11（左）、u22（中）及u33（右）Fig.1 Eigenfunctions u11（left），u22（middle）and u33（right）

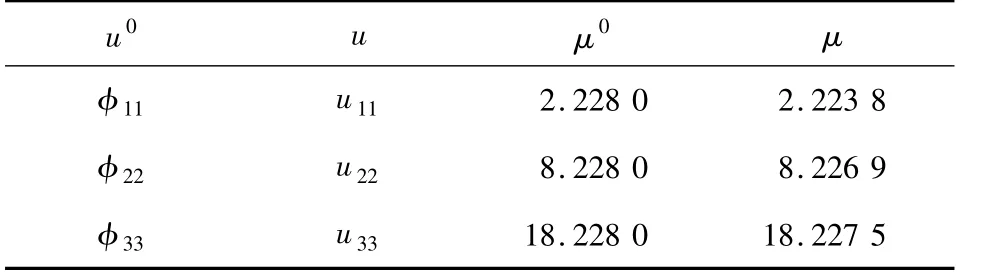
表1 圖1 所示特征函數u對應的特征值μ及初值（u0，μ0）Tab.1 Eigenvalues μ corresponding to eigenfunctions u shown in Fig.1 and their initial guesses（u0，μ0）

2）重特征情形.取

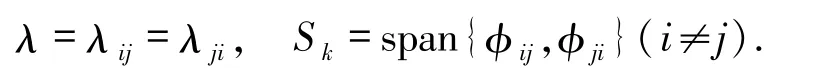
根據定理3.1，算法第二步得到32-1 =8 個特征對的初值

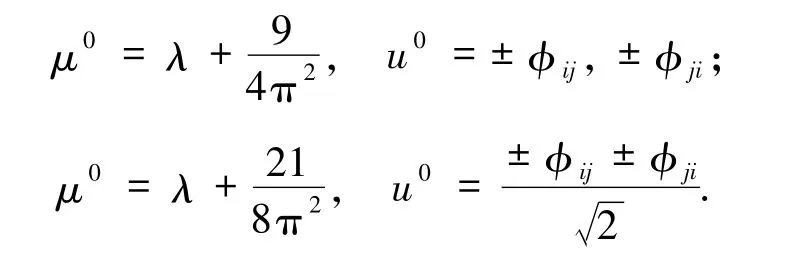
由此得到8 個（9）式的特征對數值解.對（i，j）=（1，2），（1，3）和（1，5），對應的幾種特征函數的數值解圖像繪于圖2 ～4，相應的特征值和初值信息列于表2.

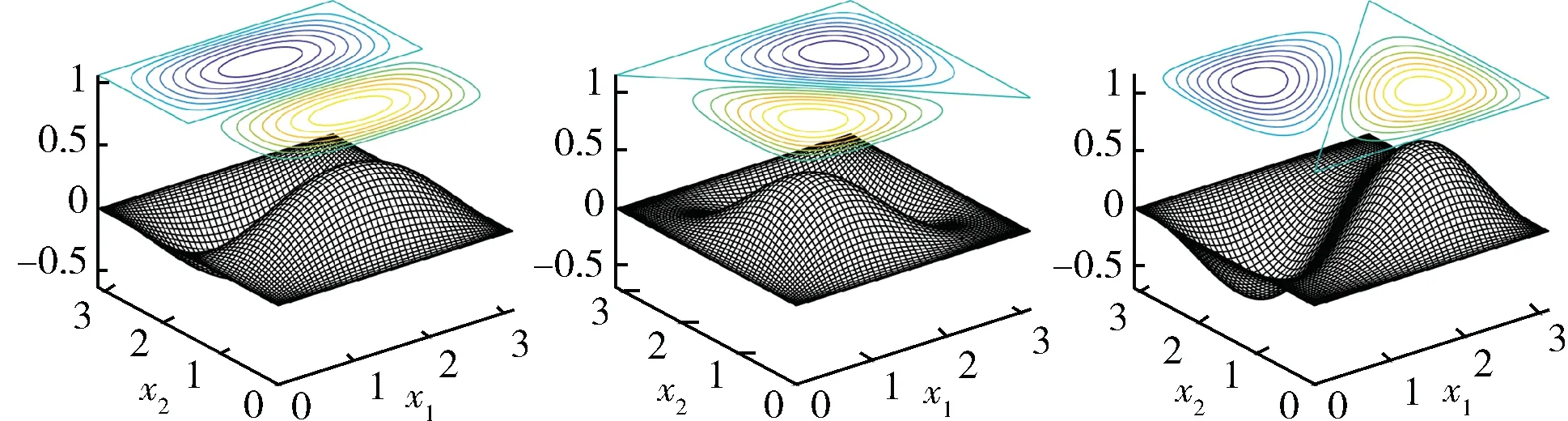
圖2 特征函數u12（左）、u12+21（中）及u12-21（右）Fig.2 Eigenfunctions u12（left），u12+21（middle）and u12-21（right）

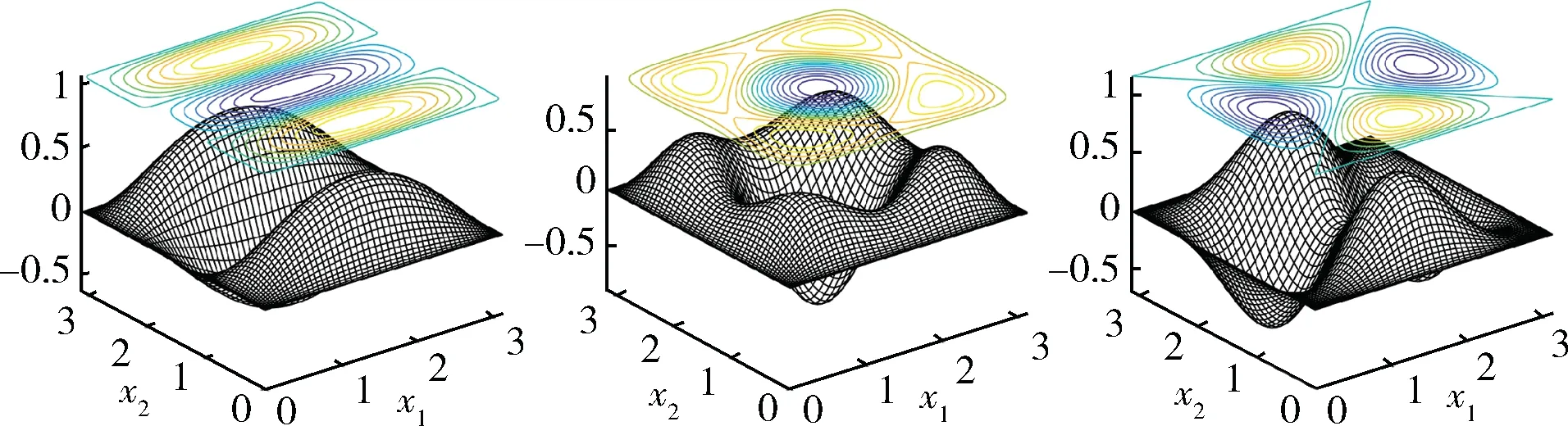
圖3 特征函數u13（左）、u13+31（中）、及u13-31（右）Fig.3 Eigenfunctions u13（left），u13+31（middle）and u13-31（right）

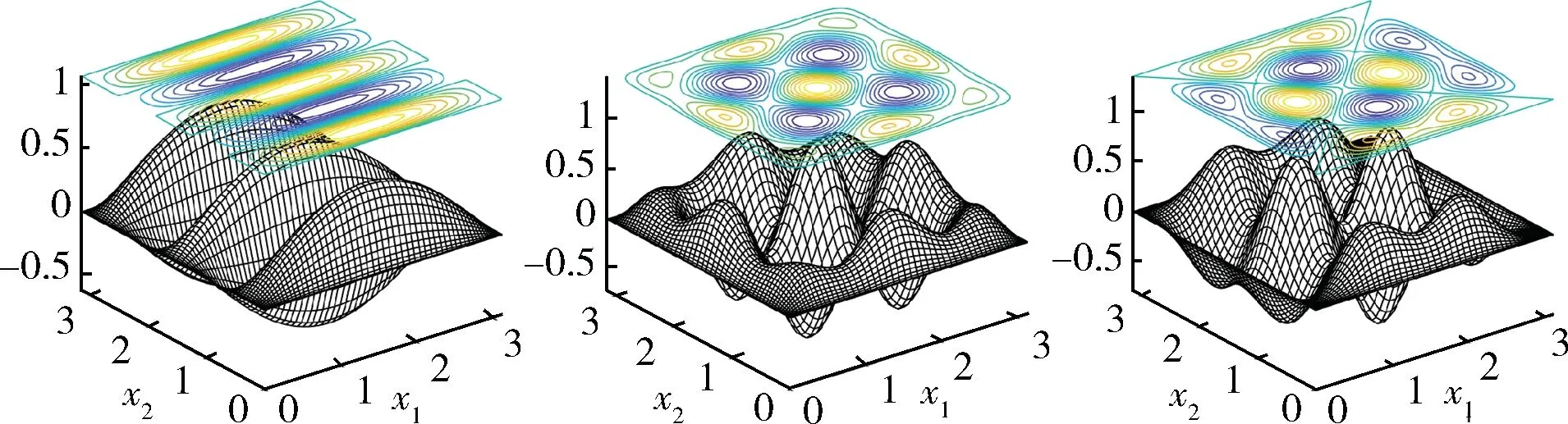
圖4 特征函數u15（左）、u15+51（中）及u15-51（右）Fig.4 Eigenfunctions u15（left），u15+51（middle）and u15-51（right）

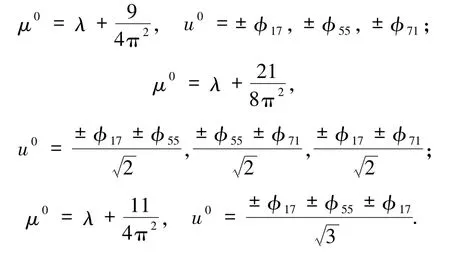
由此得到26 個（9）式的特征對數值解，其中6 種特征函數的數值解圖像繪于圖5 和6，相應的特征值和初值信息列于表3.

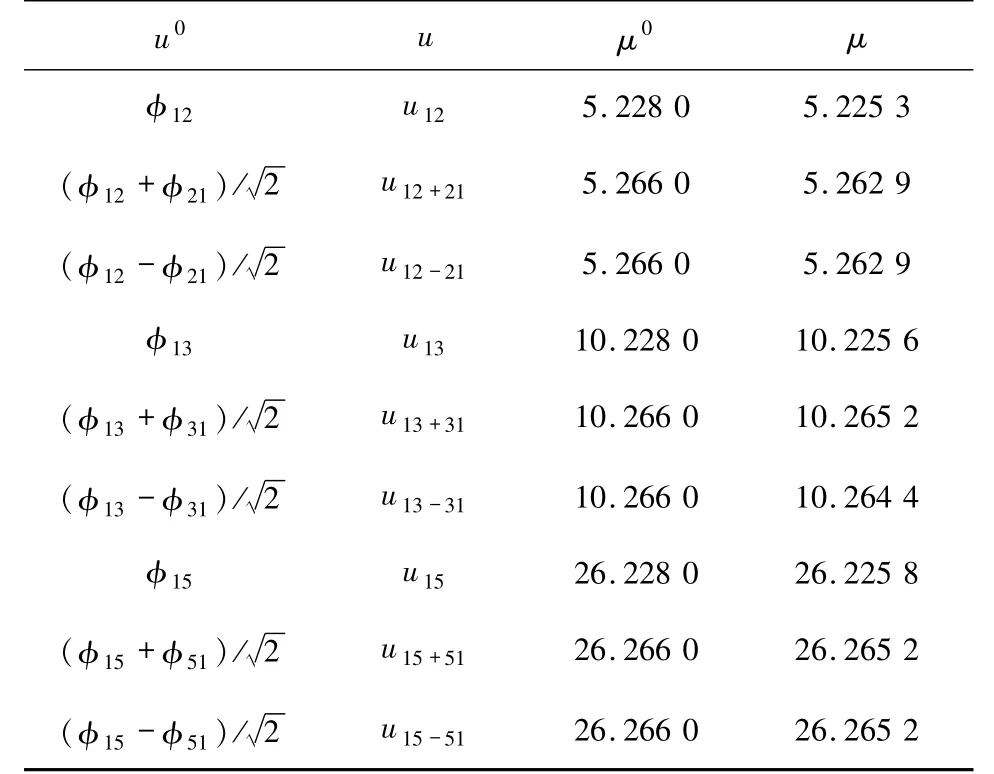
表2 圖2 ～4 所示特征函數u對應的特征值μ及初值（u0，μ0）Tab.2 Eigenvalues μ corresponding to eigenfunctions u shown in Figs.2-4 and their initial guesses（u0，μ0）

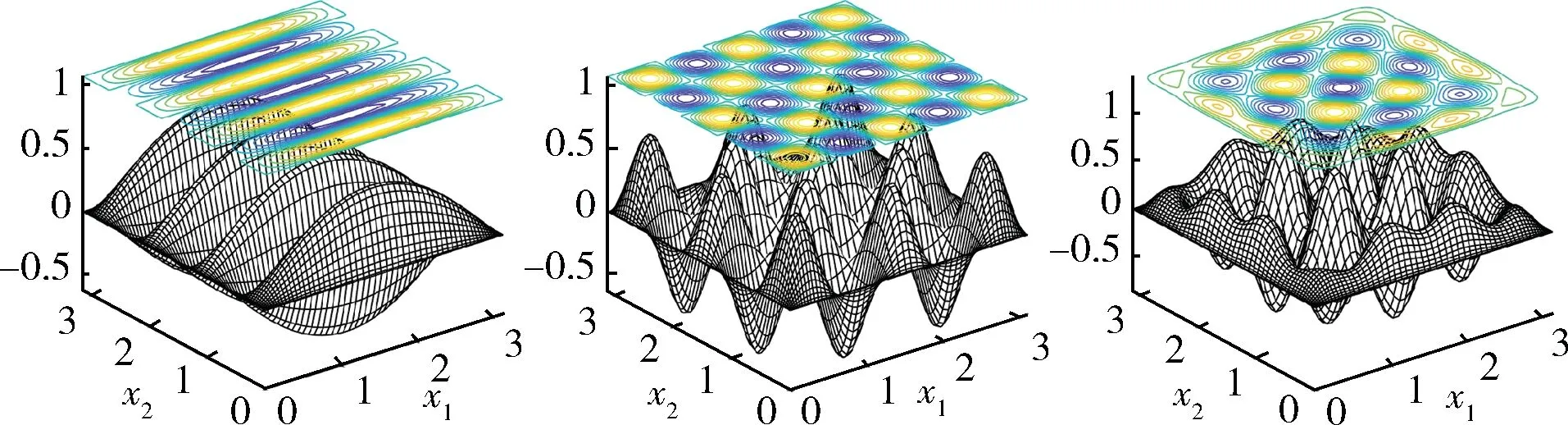
圖5 特征函數u17（左）、u55（中）及u17+71（右）Fig.5 Eigenfunctions u17（left），u55（middle）and u17+71（right）

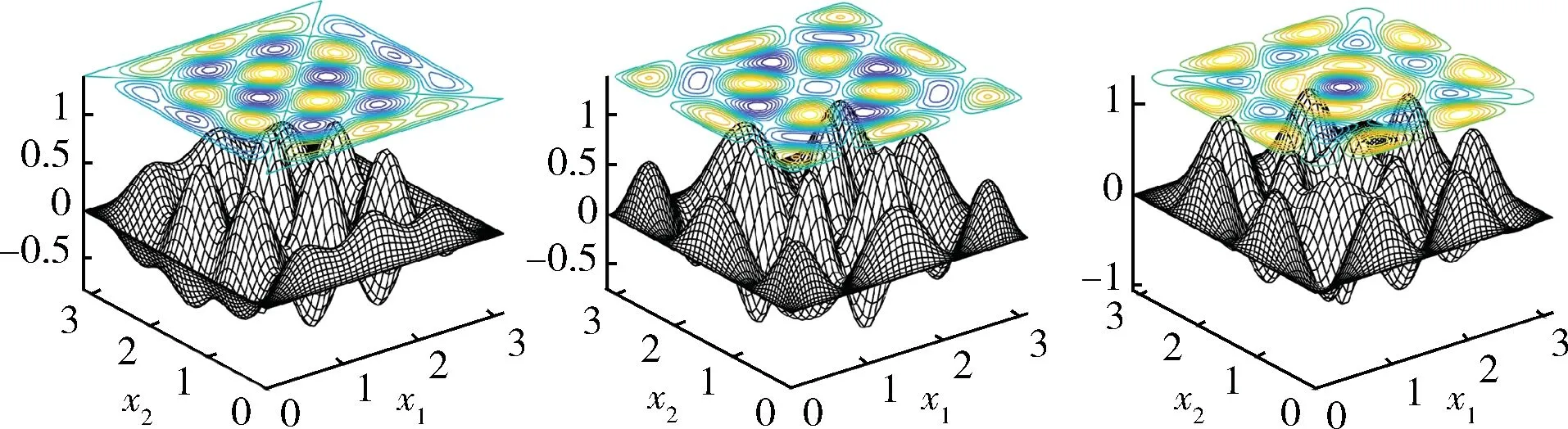
圖6 特征函數u17-71（左）、u17+55+71（中）及u17-55+71（右）Fig.6 Eigenfunctions u17-71（left），u17+55+71（middle）and u17-55+71（right）

一般地，根據定理3.1，對于-Δ的任何k重特征值λ，可在算法第二步構造3k-1 個（9）式的特征對的初值.因此，理論上可以繼續使用-Δ的更高重數的特征值和其對應的特征函數構造初值，并計算相應的特征對的數值解.然而，由于這時解的高度不穩定性，需要使用更大的逼近空間SN才能準確計算相應的數值解.例如最小的5 重特征值和最小的6 重特征值分別為

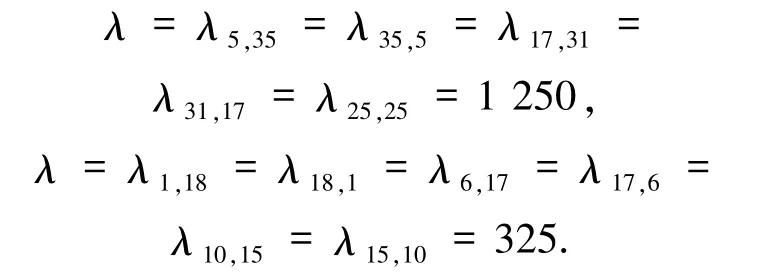
由于它們的值較大，本文暫未計算它們對應的解.

表3 圖5 ～6 所示特征函數u對應的特征值μ及初值（u0，μ0）Tab.3 Eigenvalues μ corresponding to eigenfunctions u shown in Figs.5-6 and their initial guesses（u0，μ0）

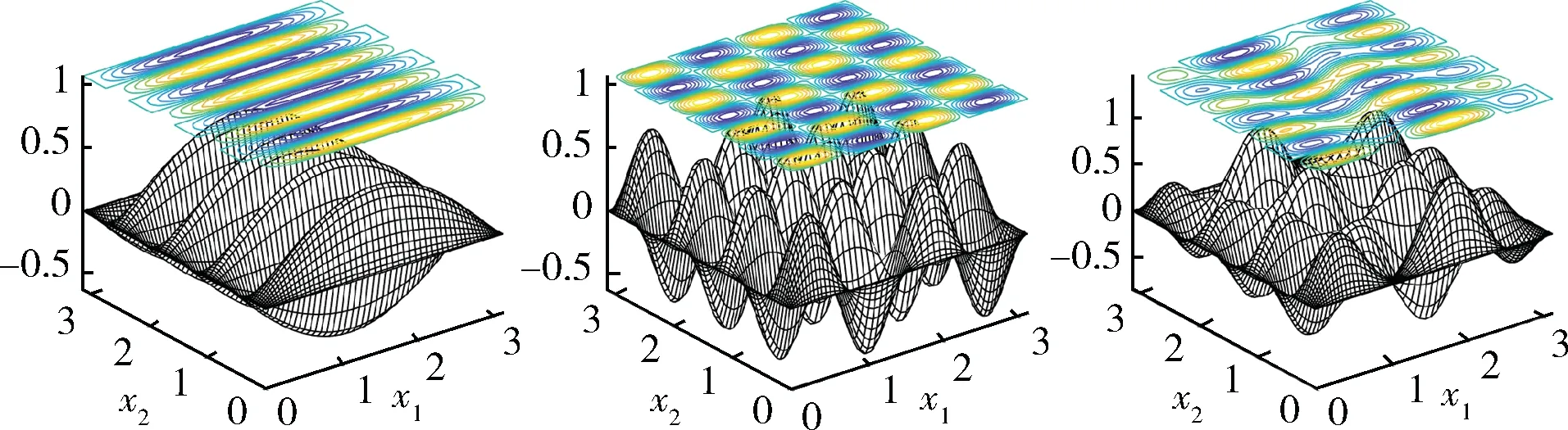
圖7 特征函數u18（左）、u47（中）及u18+47（右）Fig.7 Eigenfunctions u18（left），u47（middle）and u18+47（right）

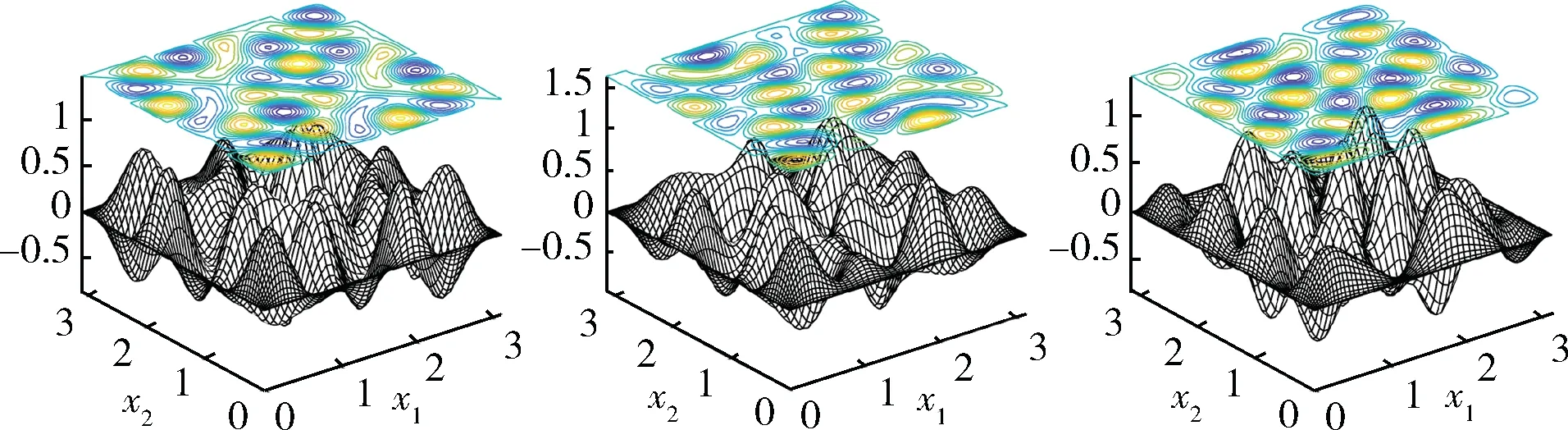
圖8 特征函數u47+74（左）、u18+47+74（中）及u18+47+81（右）Fig.8 Eigenfunctions u47+74（left），u18+47+74（middle）and u18+47+81（right）

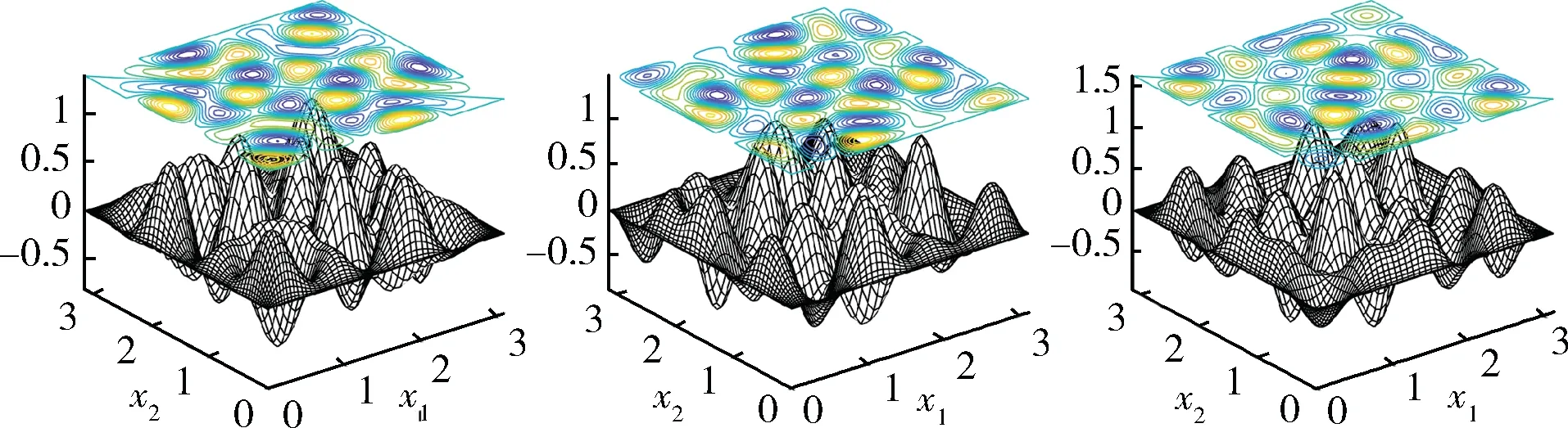
圖9 特征函數u18+47+74+81（左）、u18-47+74+81（中）及u18-47-74+81（右）Fig.9 Eigenfunctions u18+47+74+81（left），u18-47+74+81（middle）and u18-47-74+81（right）

表4 圖7 ～9 所示特征函數u對應的特征值μ及初值（u0，μ0）Tab.4 Eigenvalues μ corresponding to eigenfunctions u shown in Figs.7-9 and their initial guesses（u0，μ0）

基于上述數值結果，觀測到如下現象：

若λ是-Δ的k 重特征值，相應地，半線性特征值問題（9）至少存在3k-1 個不同的特征對（若不區分同一特征值對應的正負特征函數，則問題（9）至少存在對應于λ的（3k-1）/2 個不同的特征對）.也就是說，半線性特征值問題（9）的特征對能按-Δ特征值大小排序，且密度遠大于-Δ的特征對.它們的個數和分布類似樹形結構，且在-Δ的多重特征值的地方派生出更多樹枝.

值得一提的是，這一關于半線性特征值問題的特征對分布的數值觀測，與Chen 等［15］提出并被Zhang等［20］證明的關于立方非線性橢圓方程多解分布的猜想非常類似.對上述數值觀測的嚴格數學分析或證明還有待進一步研究.