交換半環上半線性空間的線性變換

張興均， 吳 莉， 王學平*

（1.四川師范大學 數學科學學院，四川 成都610066； 2.阿壩師范學院 數學與計算機科學學院，四川 汶川623002）

2007 年，Di Nola等［1］運用半環、半模等概念在MV-代數中引進了半線性空間的概念，得到了類似于經典線性代數中的相關結論.但也有許多與經典線性代數不同的地方，如：半線性空間的基的向量個數不再唯一、線性無關的向量組不一定能擴張為半線性空間的基等［1］.之后，許多學者開始對半線性空間的基、維數以及同構等進行了大量且細致的研究，如：2010 年，Zhao 等［2］給出了定義在交換的zerosumfree半環上L-半線性空間Vn的基的基數唯一的一個充分條件；2011 年，Shu 等［3］證明了定義在交換的zerosumfree 半環上L -半線性空間Vn的基的基數是相等的充要條件是Vn的每個向量能被基唯一表出，該充要條件還被文獻［4］進行了相應推廣，并得到了與自由基相關的一些結論.線性變換是研究半線性空間中向量之間關系的有力工具，本文主要介紹了半線性空間上線性變換、冪等變換、可逆變換的概念，定義了線性變換的運算，討論了冪等變換、可逆變換的一些基本性質，并得到了線性變換的值域與核的一些重要關系.

1 預備知識

下面將給出一些已知的基本定義.

定義1.1［5-6］半環L=（L；+，·，0，1）是滿足以下性質的代數結構：

1）（L；+，0）是交換幺半群；

2）（L；·，1）是幺半群；

3）?r，s，t∈L，r·（s +t）=r·s +r·t 與（s +t）·r=s·r+t·r成立；

4）?r∈L，0·r=r·0 =0 成立；

特別地，若?a，b∈L，都有a·b=b·a，則稱半環L為交換的.

定義1.2［5］設L=〈L，+，·，0，1〉為半環，A=〈A，+A，0A〉為交換幺半群.如果外積*：L ×A→A滿足：?r，r′∈L，a，a′∈A，

1）（r·r′）*a=r*（r′*a），

2）r*（a+Aa′）=r*a+Ar*a′，

3）（r+r′）*a=r*a+Ar′*a，

4）1*a=a，

稱半環L上的半模為L -半線性空間［1］.這里的半模或是左L-半模，或是右L -半模［6］.通常情況下，將半環中的元稱為標量或者系數，將半線性空間中的元稱為向量.

不失一般性，設以下討論的半模均為左L-半模.在不混淆的情況下，將（r·r′）*a 寫作（rr′）a.設n=｛1，2，…，n｝，則由定義1.2 可給出下面L -半線性空間的例子.

例1.1設L=〈L，+，·，0，1〉是半環.對n≥1，令

其中（a1，a2，…，an）T表示（a1，a2，…，an）的轉置.對任意的x =（x1，x2，…，xn）T，y =（y1，y2，…，yn）T∈Vn（L）和r∈L，定義

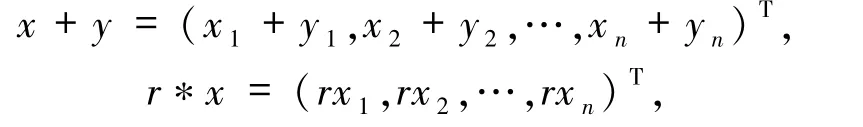
定義1.3［7］設W是L-半線性空間V的子集，若對任意的x，y∈W，k∈L，有kx∈W，x +y∈W，則稱W為L-半線性空間V的子空間.

接下來引入線性相關、線性無關以及基的概念.

定義1.4［1］設〈L，+，·，0，1；*；A，+A，0A〉為L-半線性空間.稱表達式

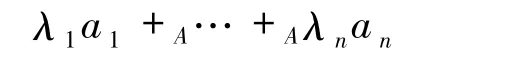
為A中向量組a1，…，an的線性組合，其中，λ1，λ2，…，λn∈L.若向量x能表示為向量組a1，…，an的線性組合，則稱向量x能被向量組a1，…，an線性表出（或線性表示）.

定義1.5［1］在L-半線性空間中，單個向量a是線性無關的.若向量組a1，…，an（n≥2）中的任意向量都不能被其余向量線性表出，則稱該向量組是線性無關的，否則，稱向量組a1，…，an是線性相關的.如果有無限個向量的向量組中任意有限個向量都是線性無關的，則稱該向量組是線性無關的.

設M是L-半線性空間V 的非空子集，如果L-半線性空間V 中任意向量都能由集合M 中向量線性表出，則稱M 是L -半線性空間V 的生成集［8］.進一步，如果M 還是有限集，則稱L -半線性空間V是有限生成的［3］.如果L-半線性空間V的元至多能被非空子集M中元以一種方式表出，則稱M 是自由的［4］.顯然，自由集一定是線性無關的.

定義1.6［4，6］稱L-半線性空間V中線性無關的生成集為V 的基.特別地，稱L -半線性空間V的自由生成集為自由基.若V存在自由基，則稱V為自由的L-半線性空間.

易見，Vn是自由的L-半線性空間.

2 線性變換

半線性空間V到自身的映射稱為V的變換.

定義2.1交換半環上L -半線性空間V 的變換A稱為線性變換，如果?a，b∈V以及?r∈L，都有：

1）A（a+b）=A（a）+A（b），

2）A（ra）=rA（a）.

注意，在文獻［9］中，稱滿足定義2.1 條件的變換為半線性變換.

例2.1設L =〈L，+，·，0，1〉是交換半環，對任意的a∈V，k∈L，定義K，則K 是線性變換.

明顯地，若半環L不是交換的，則上述例子中K不一定是線性變換.特別地，若k 為乘法單位元1，則V的變換K為，這是一個恒等變換，常用E來表示，恒等變換也叫做單位變換.若k 為加法單位元0，則V的變換K 為，這是一個零變換，常用O表示，對?a∈V，有O（a）=0.

不難從定義推出半線性空間中線性變換有如下簡單性質：

1）設A是L-半線性空間V的線性變換，則A（0）=0；

2）線性變換保持線性組合與線性關系式不變；

3）線性變換把線性相關的向量組變為線性相關的向量組.

需要注意的是3）的逆不一定成立，即半線性空間中線性變換可能將線性無關的向量組變為線性相關的向量組.

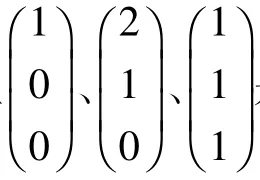
引理2.1［9］設a1，…，an是交換半環上L-半線性空間V的一組基，b1，…，bn為V中任意n個向量，則存在唯一的線性變換A使得對任意i∈n，A（ai）=bi.

定義2.2設A、B為交換半環上L-半線性空間V 中的2 個線性變換，定義它們的乘積AB：?a∈V，（AB）（a）=A（B（a）），則AB 依然是線性變換.

與經典線性代數一樣，在半線性空間中線性變換的乘法滿足結合律，但一般情況下，不滿足交換律，也不滿足消去律.

定義2.3設A、B為交換半環上L-半線性空間V 中的2 個線性變換，定義它們的加法A +B：?a∈V，（A+B）（a）=A（a）+B（a），則A+B依然是線性變換.

容易驗證，半線性空間中線性變換的加法滿足交換律與結合律，線性變換的乘法對加法滿足左右分配律.

定義2.4設A為交換半環上L -半線性空間V的線性變換，若在L-半線性空間V上存在線性變換B使得AB =BA =E，則稱變換A 為可逆的，變換B稱為A的逆變換，記作A-1.

容易驗證A-1也是線性變換，并且變換A 的逆是唯一的.

命題2.1在L-半線性空間V中，可逆線性變換把線性無關的向量組變為線性無關的向量組.

證明在L-半線性空間V中，設向量組a1，a2，…，an線性無關.若A 為V 中的可逆變換，接下來證明向量組A（a1），A（a2），…，A（an）也是線性無關的.

首先，不妨設向量組A（a1），A（a2），…，A（an）線性相關，且

A（a1）= k2A（a2）+… + knA（an），

其中k2，…，kn∈L，則根據線性變換定義有

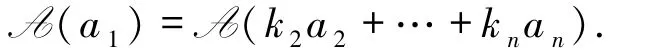
定理2.1設A 為交換半環上有限生成的L-半線性空間V的線性變換，若A 是可逆的，則a1，…，an是基當且僅當A（a1），…，A（an）也是V的基.

證明必要性 由A 是可逆變換可知，對任意的y∈V，都存在向量x∈V 使得A（x）=y.不妨設a1，…，an是V的一組基，且，其中ki∈L，i∈n，則A（x）=y=k1A（a1）+…+knA（an）.

也就是說，V 中任一向量都能被向量組A（a1），…，A（an）線性表出，并且由命題2.1 知，A（a1），…，A（an）線性無關，因此，A（a1），…，A（an）是V的一組基.

充分性 ?x∈V，有A（x）∈V，若A（a1），…，A（an）是V的一組基，則A（x）能表示成向量A（a1），…，A（an）的線性組合.不妨設A（x）= k1A（a1）+… + knA（an），其中

根據線性變換定義，有

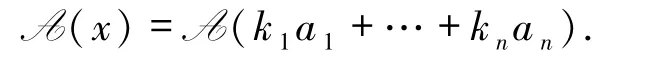
又因為A是可逆的，用A-1作用于上式兩端，則

也就是說，任意向量x都能表示為向量組a1，…，an的線性組合，又由命題2.1 知，向量組a1，…，an是線性無關的，因此a1，…，an是V的一組基.

由例2.2 易見，定理2.1 中，A 是可逆的條件一般不可去.

推論2.1A 為交換半環上有限生成的L -半線性空間V的線性變換，若A 是可逆的，則a1，…，an是V的自由基當且僅當A（a1），…，A（an）也是V的自由基.

設A為交換半環上L-半線性空間V的線性變換，n為非負整數，定義，稱為A的n次冪.特別地，定義A0=E.若A2=A，則稱A為冪等線性變換.

命題2.2設A為交換半環上L -半線性空間V的可逆冪等線性變換，則A是單位變換.

證明因為A為可逆線性變換，則有AA-1=E.又A為冪等線性變換，即A2=A，則

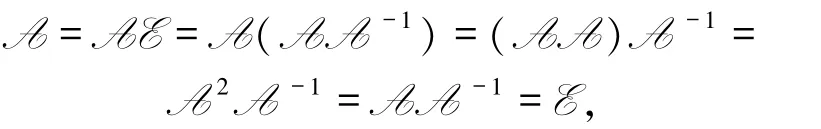
所以A=E.

3 線性變換的值域與核

設A為L-半線性空間V的線性變換，記Im（A）=｛A（a）：a∈V｝，稱Im（A）為A的值域.記Ker（A）=｛a∈V：A（a）=0｝，稱Ker（A）為A的核.

不難證明，Im（A）與Ker（A）都是L-半線性空間V的子空間.

定義3.1設A為L-半線性空間V的線性變換，W是V的子空間，若?a∈W 有A（a）∈W，則稱W是A的不變子空間.

命題3.1設A與B是L-半線性空間V的2 個線性變換，若BA = AB，則Im（A）與Ker（A）都是B的不變子空間.

證明1）?a∈Im（A），存在b∈A 使得a =A（b），于是B（a）=B（A（b））=（BA）（b）=（AB）（b）=A（B（b）），而B（b）∈V，則A（B（b））∈Im（A），即B（a）∈Im（A）.由不變子空間定義，Im（A）是B的不變子空間.

2）?a∈Ker（A），有A（a）=0.又BA =AB，則A（B（a））=（AB）（a）=B（A（a））=B（0）=0，即A（B（a））=0，于是B（a）∈Ker（A）.

由不變子空間定義，Ker（A）是B的不變子空間.

定理3.1設A 與B是L -半線性空間V 的2個線性變換，則A 與B 都是冪等的且Im（A）=Im（B）的充分必要條件是AB=B且BA=A.

證明必要性 設A 與B 都是冪等線性變換且Im（A）= Im（B），則?a ∈V，有B（a）∈Im（B）=Im（A）.存在一向量b∈V，使得B（a）=A（b），（AB）（a）=A（B（a））=A（A（b））=A2（b）=A（b）=B（a），即AB =B.同理可得BA=A.

充分性 ?a∈V，有A（a）∈Im（A）?V.由AB=B以及BA=A，可知A（a）=（BA）（a）= B（A（a））∈Im（B），從而Im（A）?Im（B）.同理可得Im（B）?Im（A），故

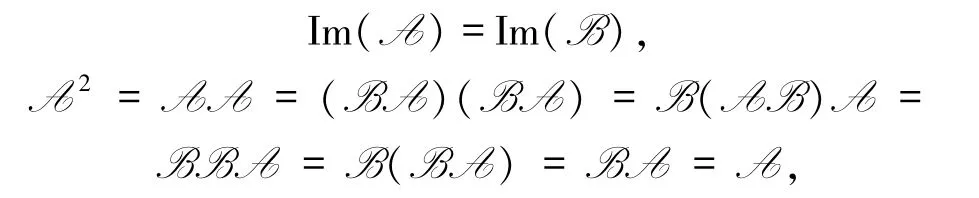
即線性變換A是冪等的.同理可得線性變換B 也是冪等的.

命題3.2設A 與B 是L -半線性空間V的2個線性變換，若AB=A且BA=B，則Ker（A）=Ker（B）.

證明?b∈Ker（A），由BA =B知，B（b）=（BA）（b）= B（A（b））= B（0）=0，所以b ∈Ker（B），從而有Ker（A）?Ker（B）.同理可得Ker（B）?Ker（A），即Ker（A）=Ker（B）.

注3.1一般說來，命題3.2 的逆命題不成立.

例3.1設L=〈L，+，·，0，1〉為半環，其中L為圖1 所示的格，+ =∨，·=∧.在L-半線性空間V2中定義A；B，其中，a∈V2，

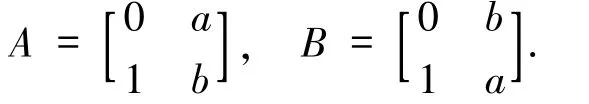
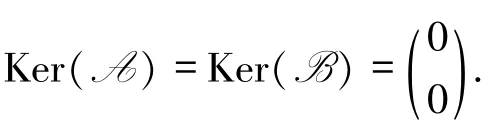
圖1 分配格Fig.1 Distributive lattice

定理3.2設A與B是有限生成的L-半線性空間V的2 個線性變換，則Im（B）?Im（A）的充分必要條件是存在線性變換C使得B=AC.

證明必要性 若Im（B）?Im（A）.設a1，…，an是V 的一組基，則存在V 中的一個向量組b1，…，bn使得B（a1，…，an）=（Ba1，…，Ban）=（Ab1，…，Abn）=A（b1，…，bn）.又由引理2.1知，存在V 中的線性變換C 使得C（a1，…，an）=（b1，…，bn），所以B（a1，…，an）=A（b1，…，bn）=AC（a1，…，an）.由于a1，…，an是L -半線性空間V的基，故B=AC.

充分性 假設V中存在線性變換C 使得B =AC，則?a∈V，有B（a）=AC（a）=A（C（a））.由于C（a）∈V，因此，A（C（a））∈A（V），即B（a）∈A（V），所以Im（B）?Im（A）.

注3.2定理3.2 中線性變換C一般不唯一.

例3.2考慮模8 的剩余類環上的線性空間V2，作V2上的線性變換A、B、C1、C2如下顯然

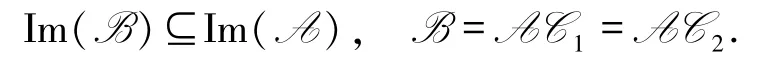
命題3.3設A與B是L-半線性空間V的2個線性變換，若在V中存在線性變換C使得CA=B，則Ker（A）?Ker（B）.

證明若在L-半線性空間V中存在線性變換C使得CA =B，則?a∈Ker（A），有A（a）=0，（CA）（a）=C（A（a））=C（0）=0，即B（a）=0，所以a∈Ker（B），即Ker（A）?Ker（B）.

注3.3一般說來，命題3.3 的逆命題不成立.

例3.3設L為例3.1中半環，在L-半線性空間V2中定義A；B：，其中，a∈V2，

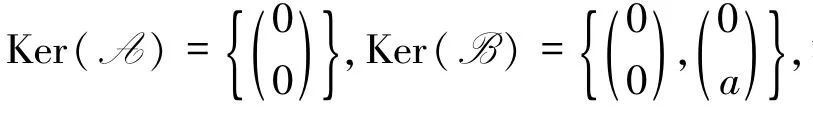
由定理3.2 與命題3.3 可得下面推論成立.

推論3.1設A與B是有限生成的L-半線性空間V的2 個線性變換，則Im（AB）?Im（A），Ker（B）?Ker（AB）.

定理3.3設A與B是L-半線性空間V的2 個線性變換，Im（B）?Ker（A）的充分必要條件是AB=O.特別地，Im（A）?Ker（A）的充分必要條件是A2=O.

證明必要性 因為有Im（B）?Ker（A），?a∈V，則B（a）∈Im（B）?Ker（A），即A（B（a））=（AB）（a）=0.

由a的任意性知AB=O.

充分性 設AB=O，在Im（B）中任取一向量B（a），a∈V，則A（B（a））=（AB）（a）=O（a）=0.

因此B（a）∈Ker（A），即Im（B）?Ker（A）.

特別地，令B=A，則有

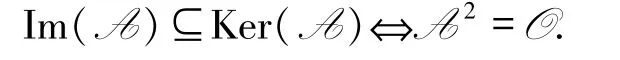
由定理3.3 易見下面推論成立.

推論3.2設A與B是L-半線性空間V的2 個線性變換，則B（Ker（AB））?Ker（A）.特別地，A（Ker（A2））?Ker（A）.

推論3.3設A與B是L-半線性空間V的2 個線性變換，若A2=O 且Im（B）=Im（A），則AB=O且Im（B）?Ker（A）.

證明若A2=O，則由定理3.3 知，Im（A）?Ker（A），又Im（B）=Im（A），所以有Im（B）=Im（A）?Ker（A）.

再根據定理3.3 得AB=O.

根據定理3.3 及推論3.3 得下面推論成立.

推論3.4設A 與B是L -半線性空間V 的2個線性變換，若A2=B2=O 且Im（B）=Im（A），則AB=BA=O且

設V1、V2是L-半線性空間V的子空間，所謂V1與V2的和，是指由所有能表示為（其中x1∈V1，x2∈V2）的向量組成的子集合，記作

推論3.5設A與B是L-半線性空間V的2 個線性變換，則A2=B2=O 與AB =BA =O同時成立的充分必要條件是

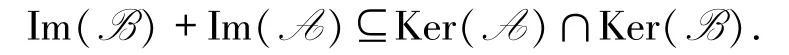
證明因為A2=B2=O，AB =BA =O，則根據定理3.3 知

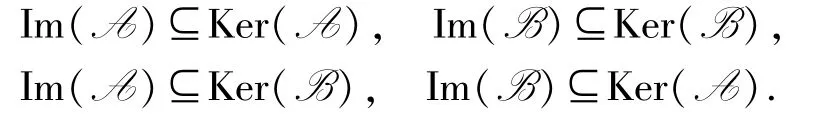
因此

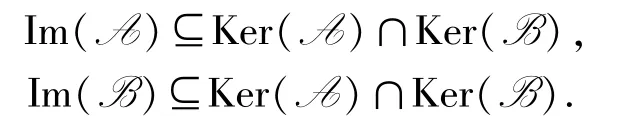
從而

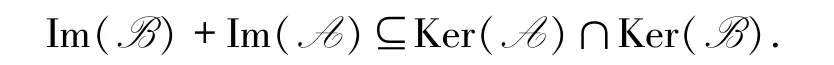
反之，設

則

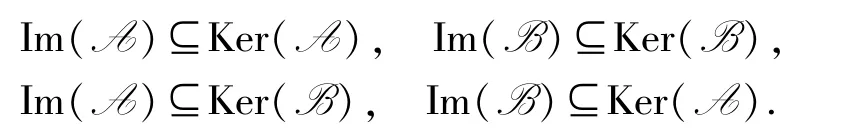
由定理3.3 得

定理3.4設A與B是L-半線性空間V的2個線性變換，則Ker（A）?Im（B）的充分必要條件是Ker（A）=B（Ker（AB））.特別地，Ker（A）?Im（A）的充分必要條件是

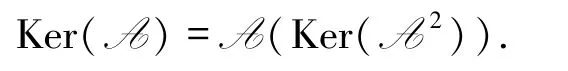
證明必要性 設Ker（A）?Im（B），?a∈Ker（A），有A（a）=0.由于a∈Ker（A）?Im（B），所以a∈Im（B），則存在向量b∈V，使a=B（b）.因此（AB）（b）= A（B（b））= A（a）=0，所以b ∈Ker（AB）.從而有a=B（b）∈B（Ker（AB）），又a∈Ker（A），所以Ker（A）?B（Ker（AB））.

另一方面，若?c∈B（Ker（AB）），則存在向量d∈Ker（AB）使得B（d）=c，（AB）（d）=0.因此A（c）= A（B（d））=（AB）（d）=0，即c∈Ker（A），所以B（Ker（AB））?Ker（A），即

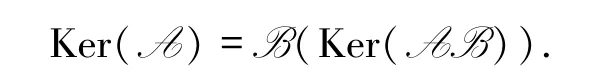
充分性 設Ker（A）=B（Ker（AB）），顯然Ker（A）= B（Ker（AB））?Im（B）.特別地，令B=A，顯然

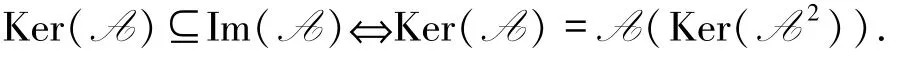
定理3.5設A為有限生成的L -半線性空間V的線性變換，若A 是單變換，則Im（A）的基的原像構成V的基.

證明由題設易知Im（A）= V，因此結論成立.

注3.4一般說來，定理3.5 中單變換條件不可去.