一類含有未知函數差分的三重和差分不等式中未知函數的估計
黃星壽, 王五生, 羅日才
(河池學院 數學與統計學院,廣西 宜州546300)
Gronwall - Bellman[1-2]型積分不等式及其推廣形式是研究微分方程、積分方程和微分-積分方程解的存在性、有界性和唯一性等定性性質的重要工具,不斷地研究它的各種推廣形式,使其應用范圍不斷擴大.但大部分研究者研究積分號內不含未知函數導函數的積分不等式[3-8].由于積分號內包含未知函數及其導函數的積分不等式在研究微分-積分方程中具有重要作用,Pachpatte[8]研究了下面的積分號內含有未知函數及其導函數的線性積分不等式同時,隨著積分不等式理論及差分方程理論的發展,不少學者更關注Gronwall-Bellman型不等式的離散形式及其推廣形式,見參考文獻[9 - 14].Pachpatte[13]研究了以下和號內含有未知函數差分的線性和差分不等式
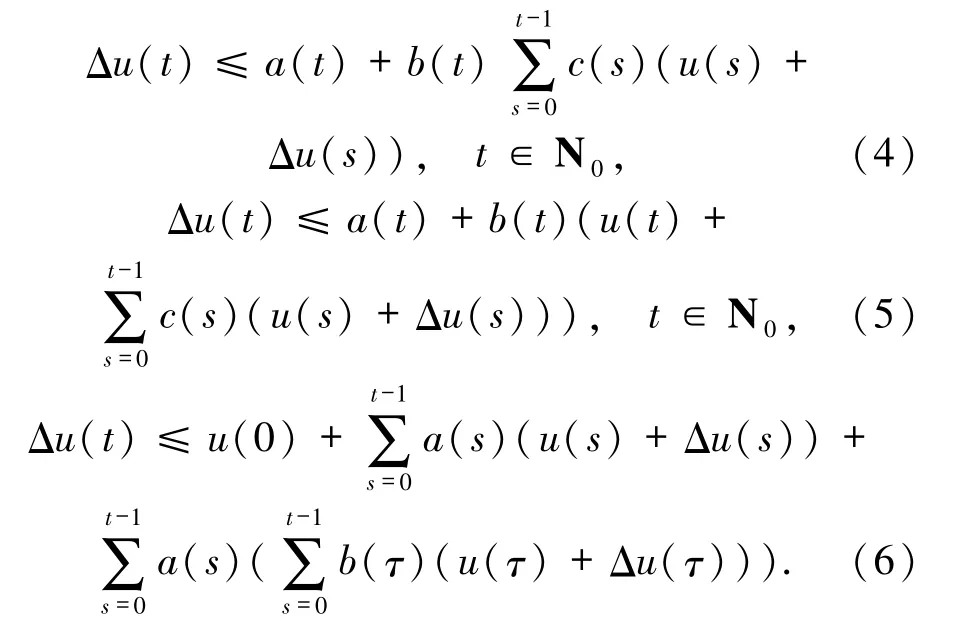
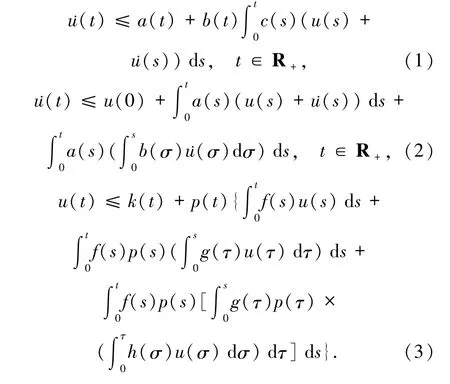
Akin-Bohner等[14]在此基礎上進一步研究T0時標(T0為實數集R上的任意非空閉子集)上的線性積分不等式
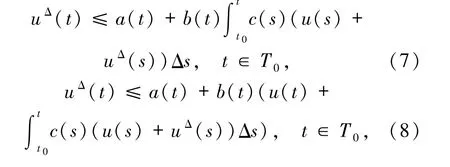
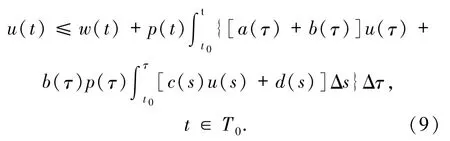
Zareen[15]更進一步研究了積分號內含有未知函數及其導函數的非線性積分不等式
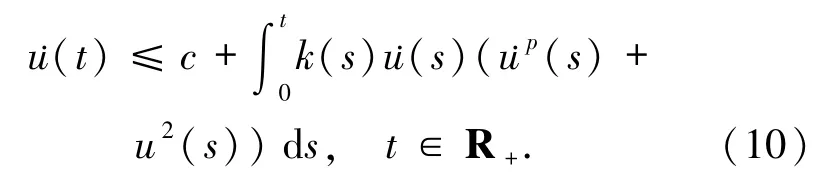
本文受文獻[13 -15]的啟發,研究了和號外具有非常數因子,且和號內含有未知函數及其差分的非線性三重和差分不等式
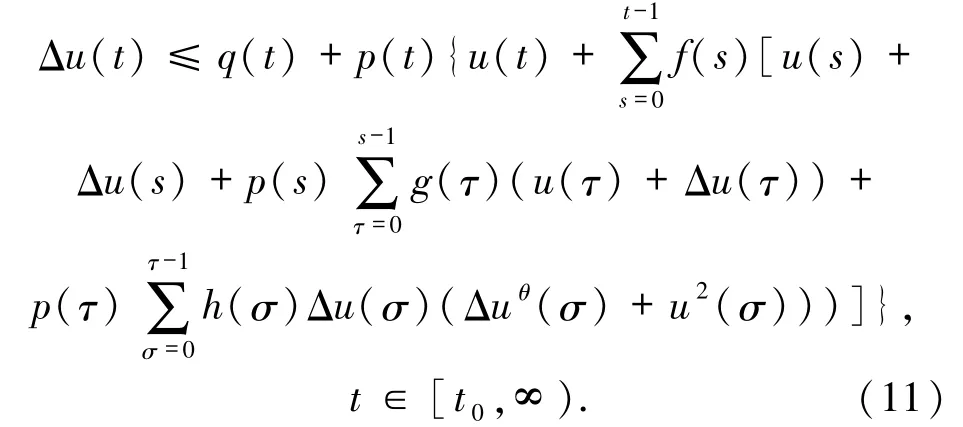
不等式(11)把文獻[13]中的不等式(6)推廣成非線性和差分不等式,把文獻[15]中的不等式(10)推廣成和號外具有非常數因子的和差分不等式.本文綜合利用分析技巧給出了不等式(11)中未知函數的估計.最后,通過例子說明其結果可以用來研究相應類型的和差分方程解的性質.
1 主要結果與證明
為了使結果的證明過程簡單明了,先給出以下引理.
引理1[16-17]令y≥0,p≥q≥0 和p≠0,則對任意K >0 有關系式
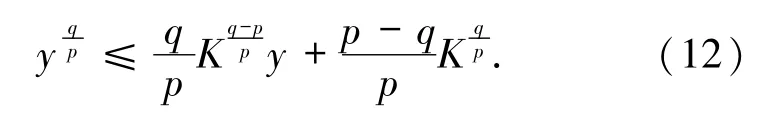
引理2假設函數u(t)、b(t)、c(t)、d(t)都是定義在自然數集合N 上的非負函數,函數a(t)是定義在自然數集合N上正的增函數,且滿足不等式
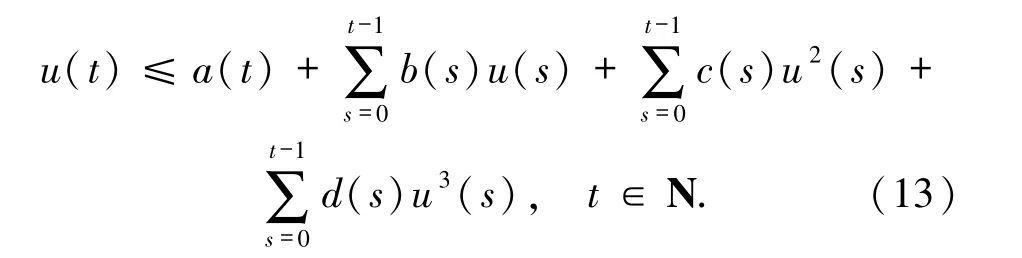
如果
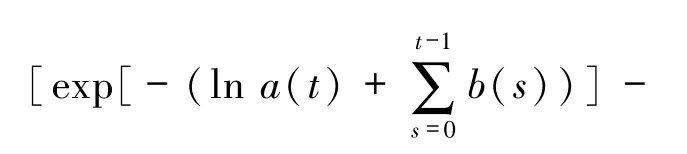

則有未知函數u(t)的估計式
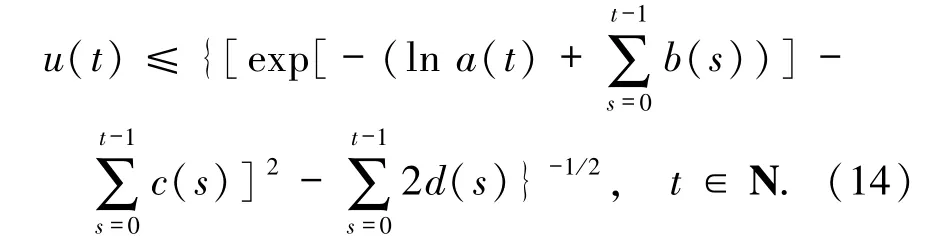
引理3[13]令u(t)、a(t)和b(t)都是定義在自然數集合N上的非負函數,且滿足

則有未知函數的估計
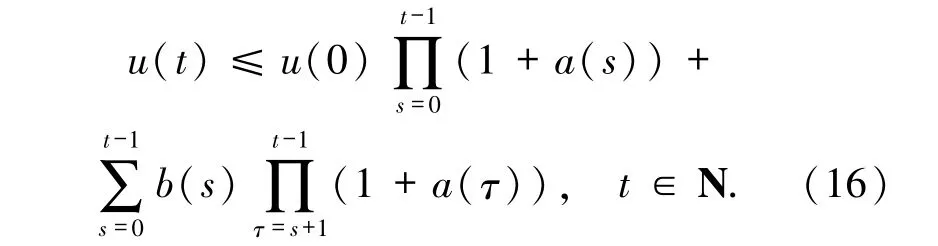
定理1假設q(t)、p(t)、f(t)、g(t)、h(t)都是定義在N 上的非負已知函數,u(0),是正常數,u(t)和Δu(t)是定義在N上的滿足不等式(11)的未知函數.對于任意t∈N,如果
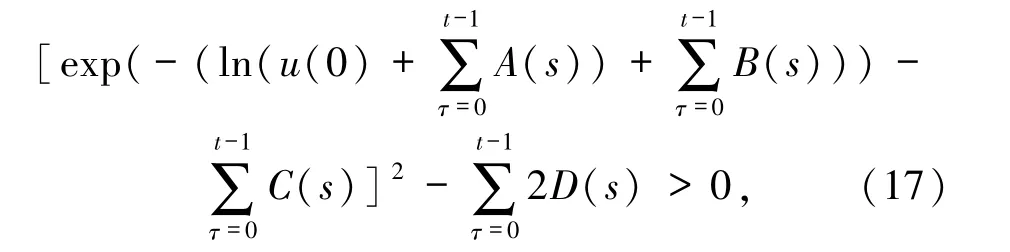
則對于任意K >0,有不等式(11)中未知函數估計式
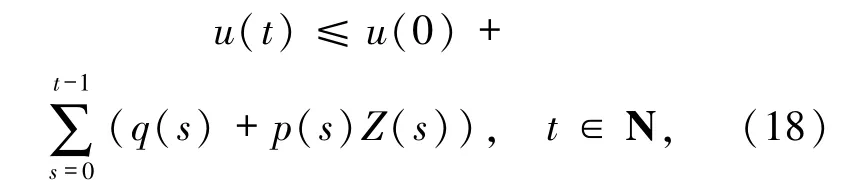
其中
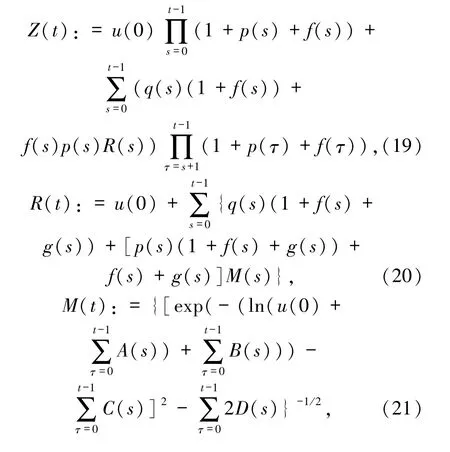
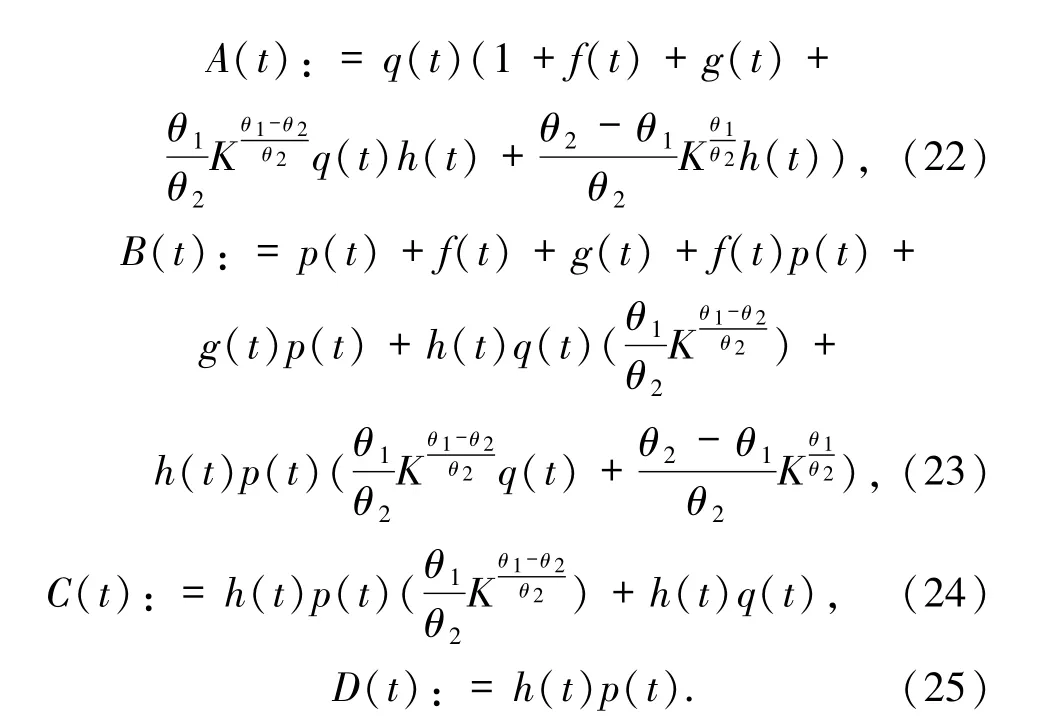
證明由不等式(11)定義函數z(t)為:
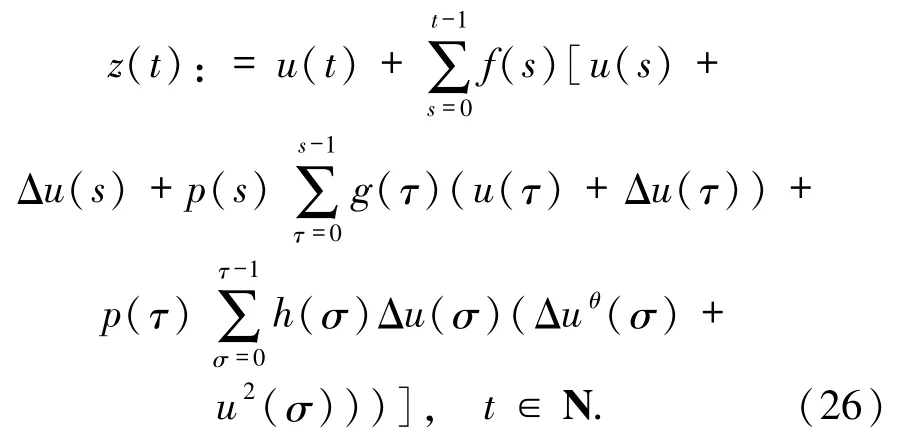
由(11)和(26)式可看出z(t)是非減函數,且有
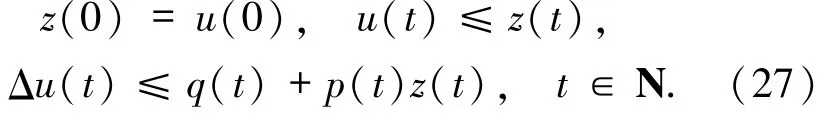
先求函數z(t)的差分,利用(26)式得到
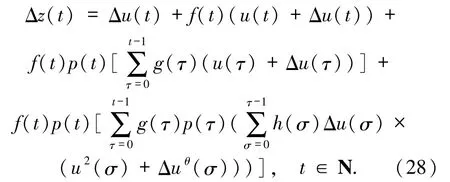
把(27)式代入(28)式得到
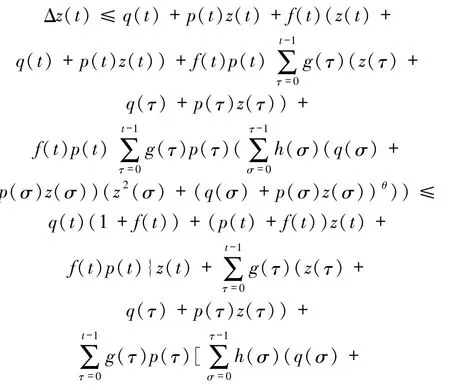
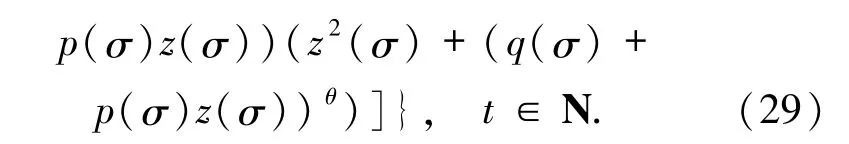
再定義函數r(t)為:

從定義式(30)可以看出r(t)是非減函數,且有
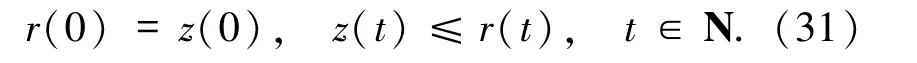
把(30)和(31)式代入(29)式得
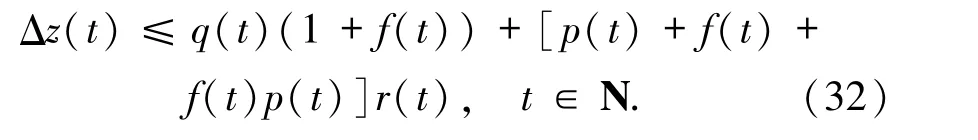
再求函數r(t)的差分得
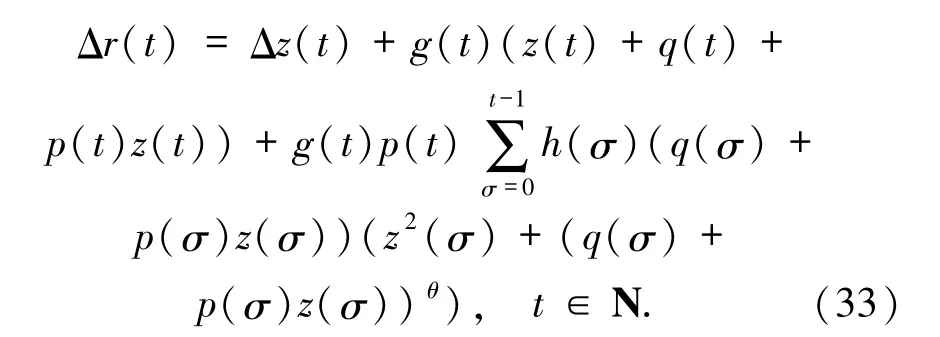
再把(31)和(32)式代入(33)式得
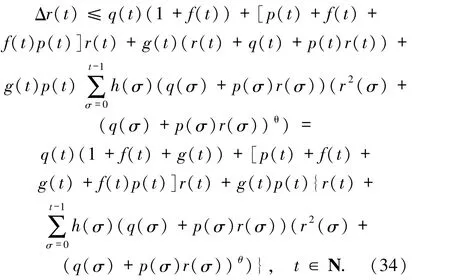
為了進一步簡化,再定義函數m(t)為:
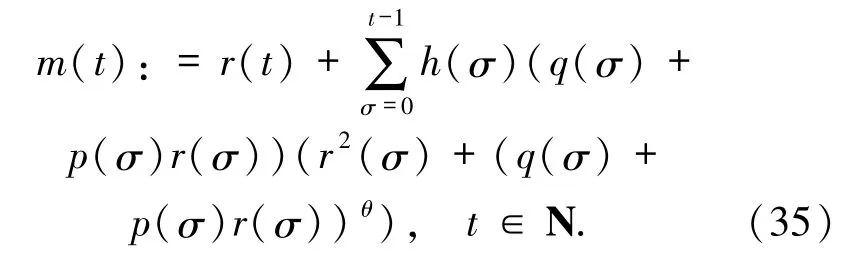
從定義式(35)可以看出m(t)是非減函數,且有
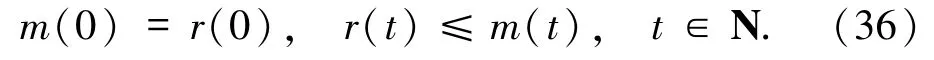
求函數m(t)的差分,利用(34)~(36)式得
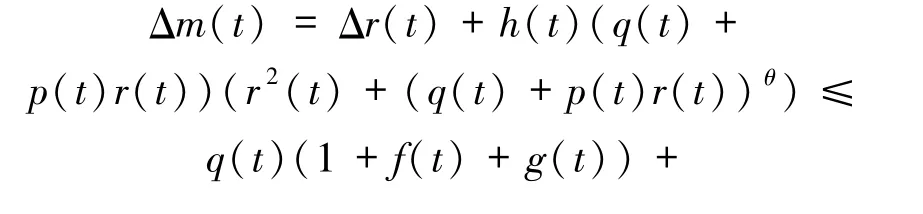
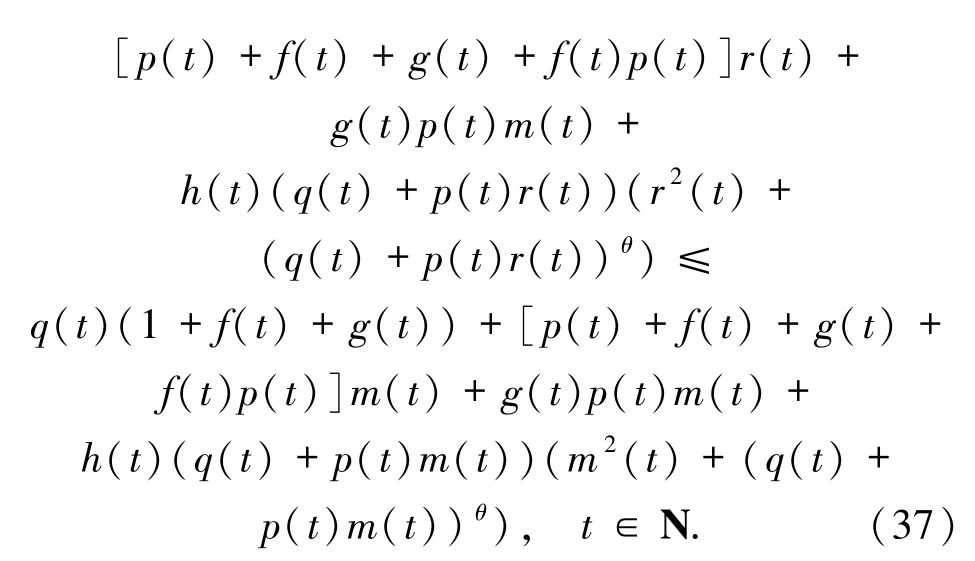
對于任意K >0,利用引理1 可以推出
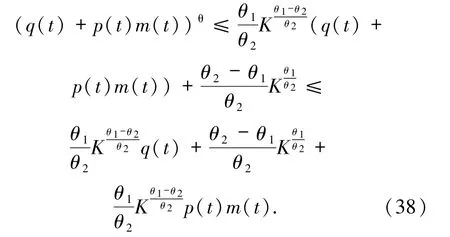
把(39)式代入(37)式可得
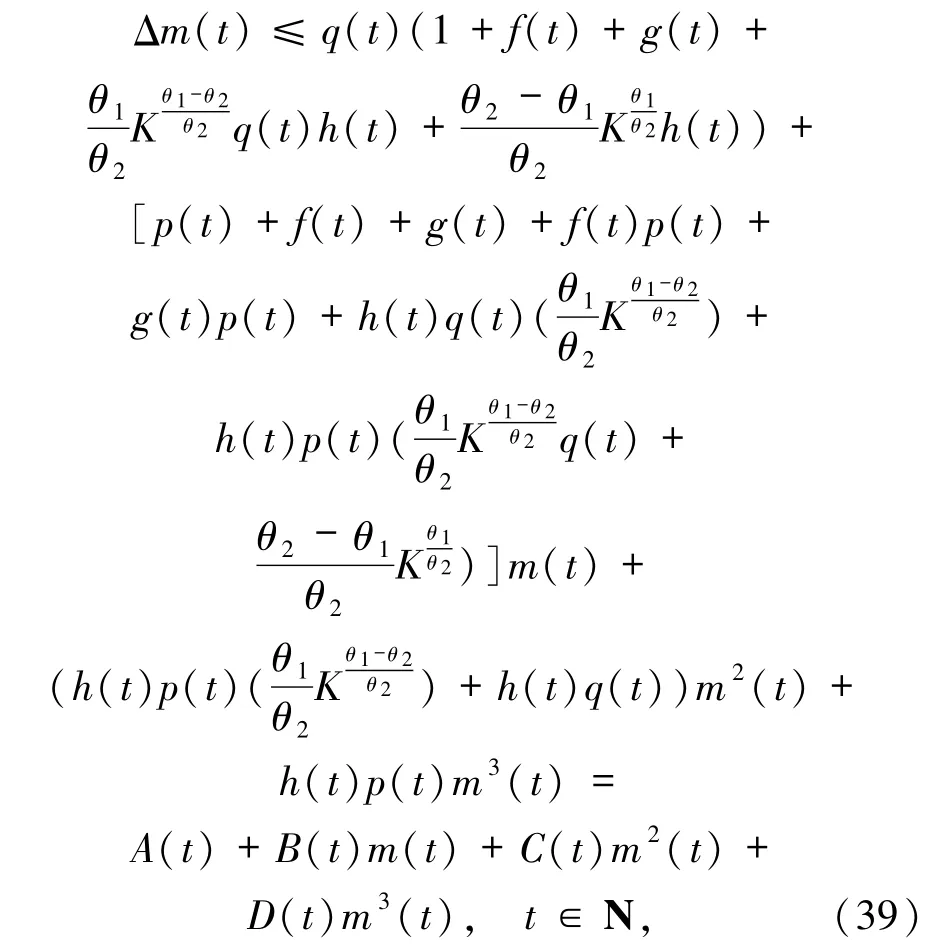
其中,A(t)、B(t)、C(t)由定理中的(22)~(25)式定義.先把不等式(39)中的t改寫成s,然后對不等式兩邊關于s從t0到t-1 求和,得到
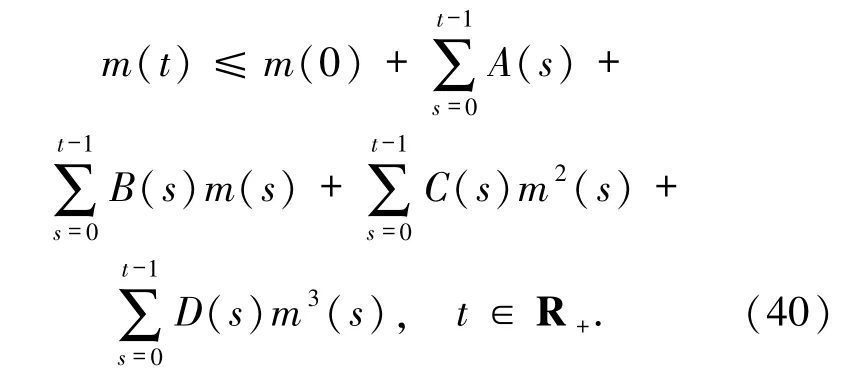
利用(27)、(31)和(36)式,(40)式改寫成
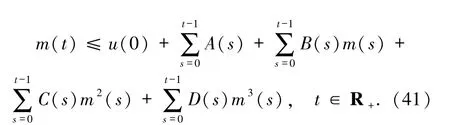
由于(41)式具有引理2 中不等式(13)的形式,且相關函數滿足引理2 中的相應條件,利用引理2 就可以得到不等式(41)中m的估計
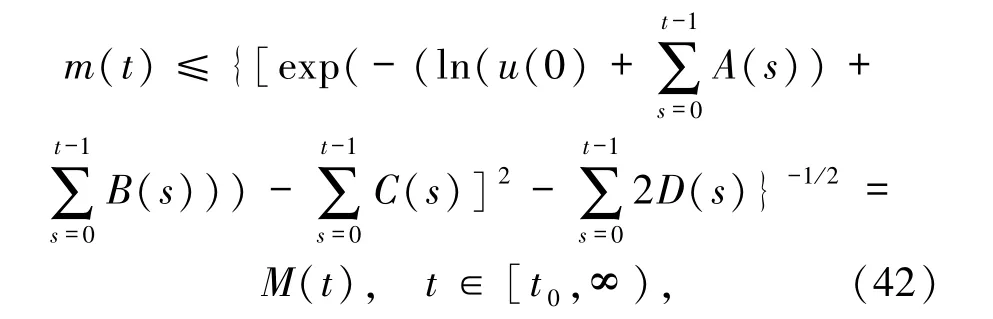
其中,M(t)由定理中的(21)式定義.把(36)和(42)式代入(34)式,可得
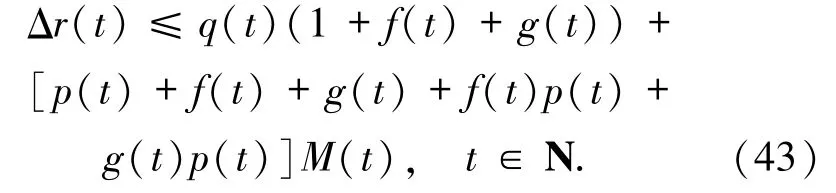
由(27)、(31)和(43)式得到
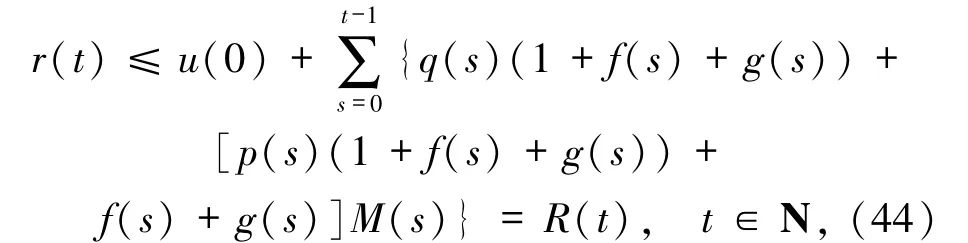
其中R(t)由定理中(20)式定義.把(44)式代入(29)式可得
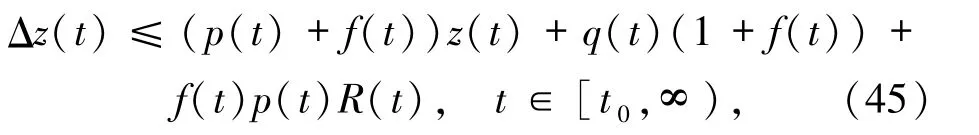
不等式(45)具有引理3 中不等式(15)的形式,且相關函數滿足引理3 中的相應條件,利用引理3 就可以得到不等式(45)中z的估計
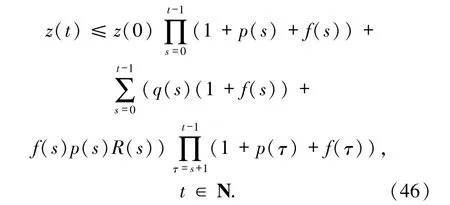
利用(27)式得到
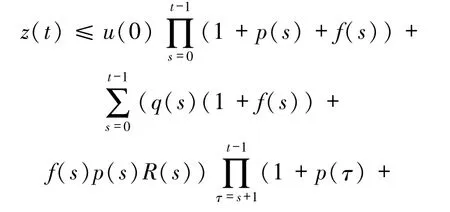
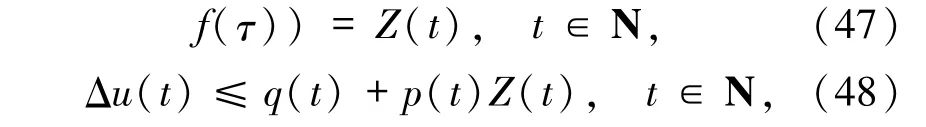
其中Z(t)由定理中(19)式定義.由(48)式得到定理所要求的u(t)估計式(18).
2 應用
本文結果可以用來研究相應類型的和差分方程解的性質.現在考慮和差分方程
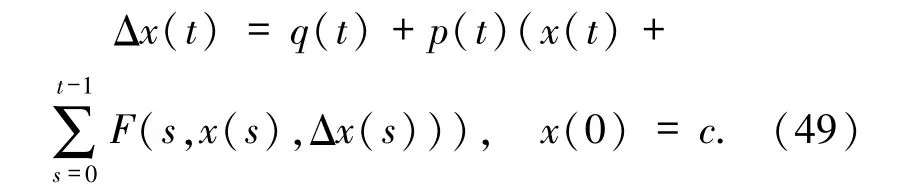
推論1假設方程(49)中|c |是正常數,q(t)、p(t)和定理1 中q(t)、p(t)的定義相同.F∈C(N×R×R,R)滿足下列條件
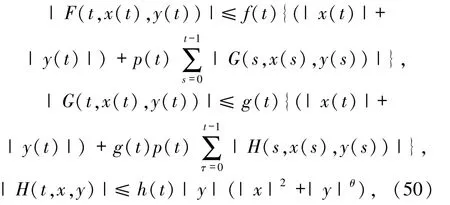
其中,f(t)、g(t)、h(t)和θ如定理1 中的定義.假設|c|、q(t)、p(t)、f(t)、g(t)、h(t)和θ滿足
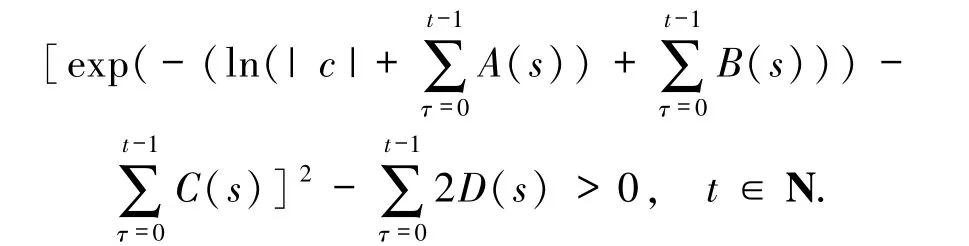
如果x(t)是方程(49)的解,則對于任意K >0,方程(49)解的模的估計式
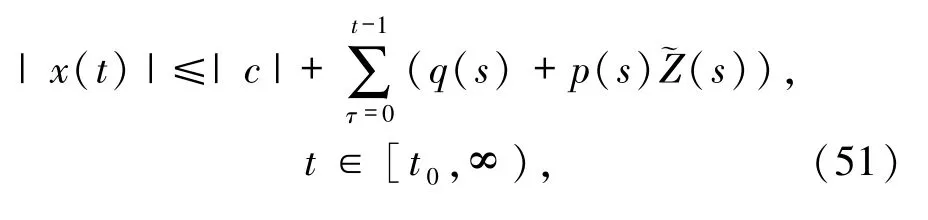
其中
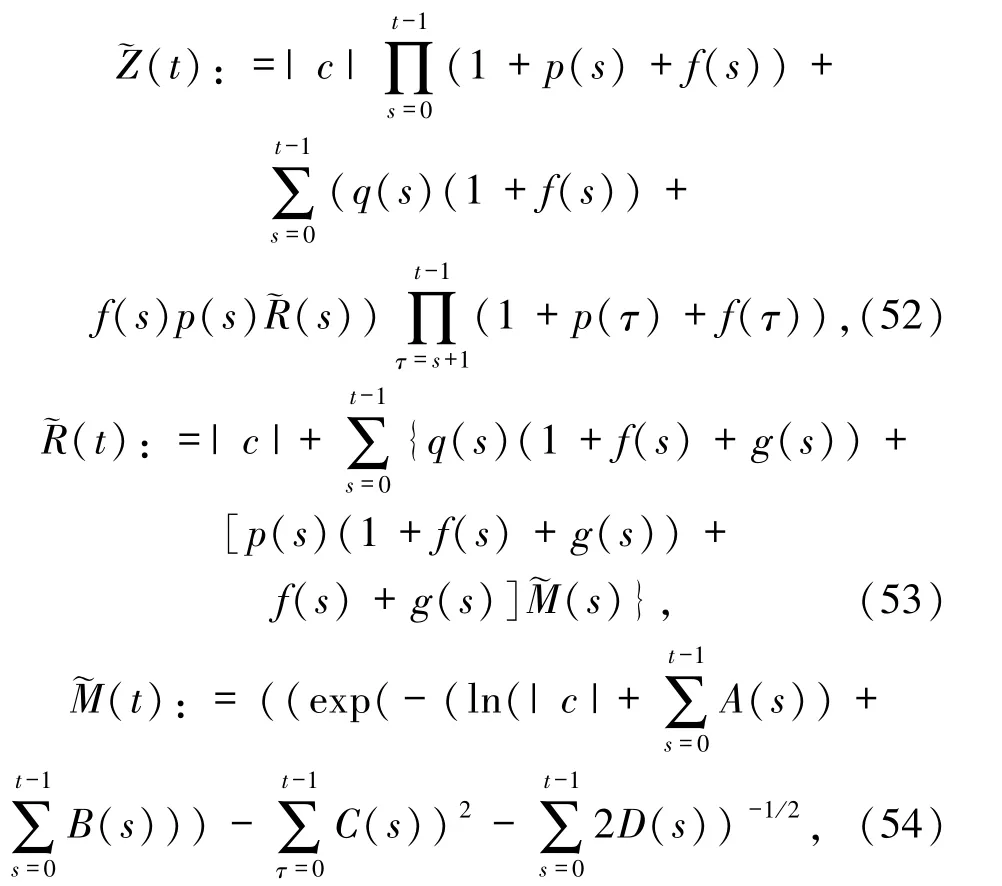
A(t)、B(t)、C(t)、D(t)分別由定理1 中的(22)~(25)式定義.
證明利用條件(52)~(54),由方程(49)推出
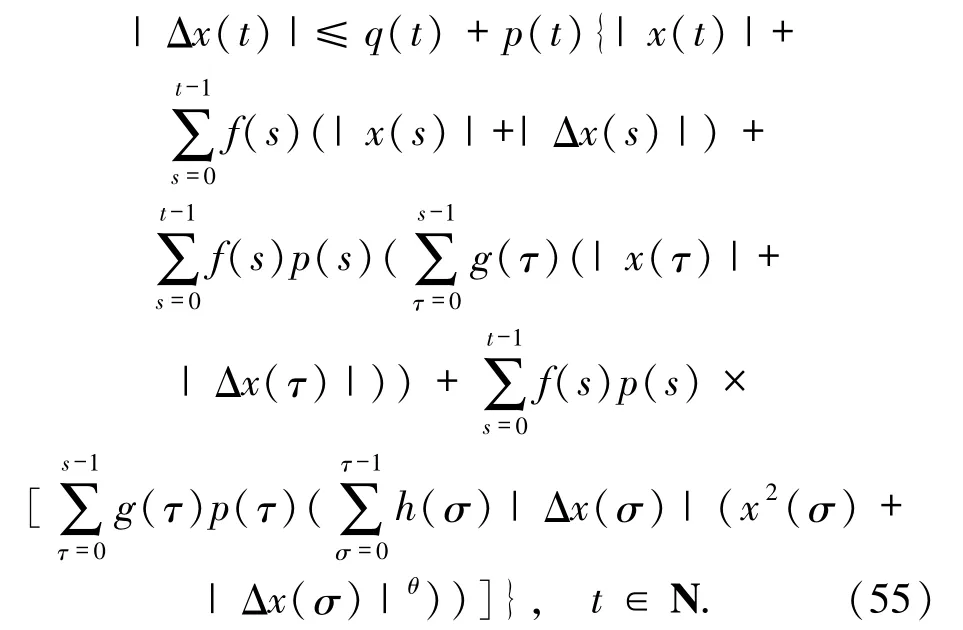
由于(55)式具有不等式(11)的形式,且滿足定理1中的相應條件,利用定理1 就可以得到所求的方程解的模的估計式(51).

