非最大糾纏GHZ 態的受控量子隱形傳態

王 娜， 章志華*， 張嘉敏， 舒 蘭

（1.江蘇大學 理學院，江蘇 鎮江212013； 2.電子科技大學 數學科學學院，四川 成都611731）

量子隱形傳態方案最早在1993 年由Bennett等［1］提出.此方案中有一待傳送的單量子未知態，發送者和接收者共享一個EPR 對作為量子糾纏信道.發送者對自己手中的粒子進行一次Bell基測量并通過經典信道將測量結果告訴接收者.接收者作相應幺正變換重構待傳送態，從而完成隱形傳態.此后，許多學者開始了對隱形傳態的研究：Cao等［2］利用W 態作為信道實現二粒子隱形傳態，Yang等［3］提出三粒子糾纏態隱形傳態方案；特別地，Nielsen［4］提出了以非最大糾纏態作為量子信道實現隱形傳態，隨后關于這方面的方案也相繼被提出.

可控量子隱形傳態是在1998 年由Karlesson等［5］首次提出，其中利用的量子信道為GHZ態.在可控量子隱形傳態中除了發送者和接收者還多了一個控制者，發送者想將信息傳送給接收者需要向控制者提出申請，待控制者同意后才能進行隱形傳態.近年來，一些可控隱形傳態方案被相繼提出.劉俊昌等［6］基于糾纏交換和團簇態實現任意二粒子態的可控隱形傳態，胡鈺安等［7］提出基于四粒子GHZ態的可控量子雙向隱形傳態方案.

在量子隱形傳態中，三粒子糾纏態的隱形傳態一直是人們研究的熱點問題.Dur 等［8］在研究三粒子糾纏態時發現，可將任意三粒子糾纏態轉換為糾纏GHZ態和糾纏W態，因此糾纏GHZ態的傳送成為值得研究的問題.如劉秀等［9］提出利用三粒子部分糾纏GHZ 態概率隱形傳送三粒子GHZ 態的方案，李艷玲等［10］利用單個三粒子最大GHZ 態或2個EPR態隱形傳送任意三粒子GHZ態，臧鵬等［11］利用2 個EPR對實現三粒子GHZ態的控制隱形傳態方案.W態在結構上相較GHZ態更穩定，不易被破壞［12］，W態作為信道可以提高隱形傳態的安全性.楊洪欽等［13］提出利用三粒子W態隱形傳送三粒子GHZ態的方案，查新未等［14］提出利用一個三粒子W態隱形傳送N粒子GHZ態的方案.本文考慮到隱形傳態的可控性和安全性問題，提出利用一個非最大糾纏EPR 對和一個四粒子GHZ 態、一個非最大糾纏的EPR對和W態分別作為信道隱形傳送任意三粒子GHZ態的方案.

1 方案1：利用一個非最大糾纏EPR對和一個非最大糾纏的四粒子GHZ態的隱形傳態

假定Alice和Bob傳送的未知態為GHZ態，表示為

Alice和Bob共享的量子信道為一個非最大糾纏的EPR對和一個非最大糾纏的四粒子GHZ態的復合

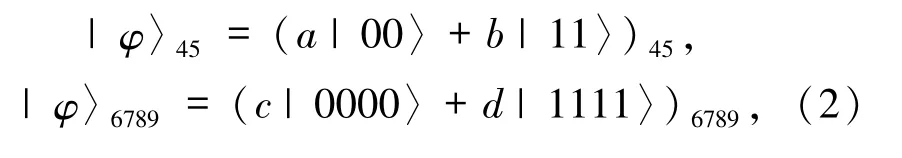
其中，參數滿足｜a ｜2+ ｜b ｜2=1 和｜c ｜2+ ｜d ｜2=1.Alice擁有粒子1、2、3、4，Bob擁有粒子6、8、9，粒子5、7 屬于控制者Charlie.量子信道為

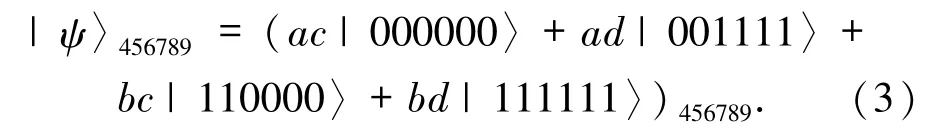
Alice要將信息傳遞給Bob 需向控制者Charlie提出申請，若Charlie 同意Alice 的申請，則對粒子5、7 進行Bell基聯合測量.Bell基形式為：

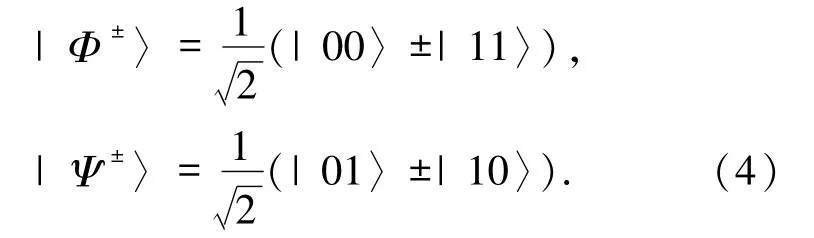
Bell基聯合測量后，粒子4、6 建立聯系.Charlie將測量結果通過經典信道告訴Bob.如果Charlie的測量結果為｜Φ+〉57，則量子信道坍縮態為

此時待傳送態和量子信道的總量子態（除歸一化因子）為

接著，Alice 對自己手中的粒子1、4 進行Bell基測量，測量后系統量子態為如下幾種情況：

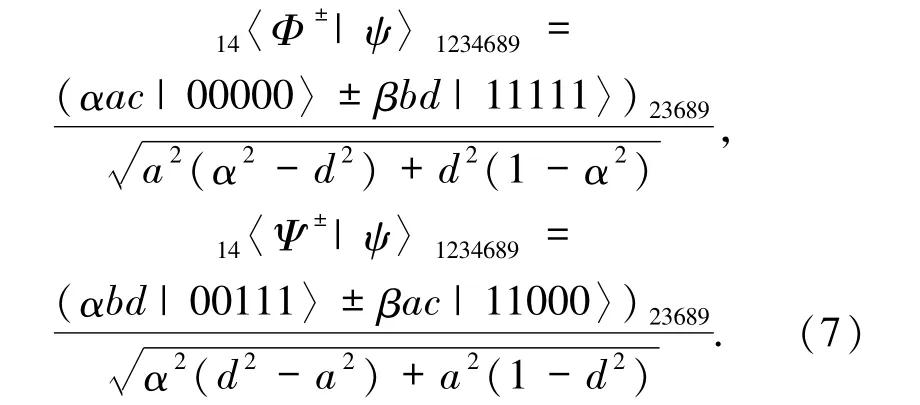
假定Alice的測量結果為｜Ψ+〉14，則量子態坍縮態為

接下來，Alice將粒子2、3 在基｛｜+〉、｜-〉｝下分別進行2 次單粒子von -Neumann 測量，測量后粒子6、8、9 坍縮態為：

Alice將測量結果通過經典信道告訴Bob，Bob根據Charlie和Alice的測量結果對粒子6、8、9 作相應的幺正變換.粒子6、8、9 的狀態（除歸一化因子）和相應的幺正變換由表1 給出，其中UT 為Unitary transformation縮寫，下同.

表1 對應粒子6、8、9 的態Bob所實施的幺正變換Tab.1 UT by Bob corresponding to different states of particle 6，8 and 9

例如，如果Charlie 的測量結果為｜Φ+〉57，Alice的測量結果為｜Ψ+〉14、｜+〉2、｜+〉3，則粒子6、8、9 的坍縮態（除歸一化因子）為

由上式可以看出，Bob 通過變換之后不能得到原來的態，因為非最大糾纏信道已使得被傳送的量子態發生變化，含有了信道參數a、b、c、d，因此引進初態為｜0〉的輔助粒子A，并且以基｛｜0000〉689A、｜1110〉689A、｜0001〉689A、｜1111〉689A｝進行U變換

其中，Ai（i=1，2）為2 ×2 的對角矩陣，表示為

其中，｜bi｜≤1，i =1，2 且其值依賴于粒子6、8、9、A的態.對于粒子6、8、9、A 所處的態（除歸一化因子），矩陣元b1、b2的取值由表2 給出.

表2 粒子6、8、9、A所處的態對應矩陣元b1、b2的值Tab.2 The states of particle 6，8，9 and A corresponding to the value of the matrix element b1 and b2

對于態

最后，Bob 對粒子A 進行測量，若測量結果為｜1〉A，則隱形傳態失敗；如果測量結果為｜0〉A，則隱形傳態成功且成功的概率為因此，方案1 的總成功概率為

2 方案2：利用非最大糾纏的EPR 對和非最大糾纏W態的隱形傳態

Alice 發送給Bob 的未知態為（1）式.Alice 和Bob共享的量子信道為一個非最大糾纏的EPR 對和一個非最大糾纏的W態，表示為

其中，參數滿足｜a｜2+ ｜b｜2+ ｜c｜2+ ｜d｜2=1， ｜e｜2+ ｜f｜2=1.

設Alice擁有粒子1、2、3、4，Bob擁有粒子6、8，粒子5、7 屬于控制者Charlie.

為了更好地完成隱形傳態，將W 態以4 粒子為控制位，5、6 粒子為靶位，分別做2 次CNOT 操作，W態變換為

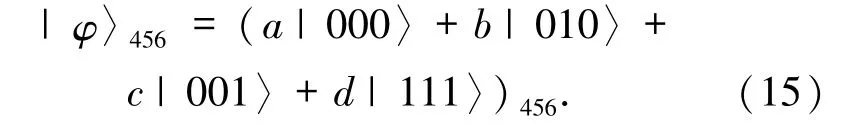
此時的量子信道為

Alice 想要將信息傳遞給Bob 就必須要向控制者Charlie提出申請，若Charlie同意Alice的申請則對粒子5、7 進行Bell 基聯合測量，Bell 基由（4）式給出.Charlie通過經典信道將測量結果告訴Bob.

假定Charlie 的測量結果為｜Φ+〉57，量子信道坍縮態（除歸一化因子）為

待傳送態和量子信道的總量子態（除歸一化因子）為

首先，Alice 對粒子1 和4 進行Bell基測量，測量后粒子2、3、6、8 坍縮態（除歸一化因子）為：

接著，Alice對粒子2、3在基｛｜+〉，｜-〉｝下分別進行單粒子von -Neumann 測量，并將測量結果通過經典信道告訴Bob.如果Bob 收到的結果為｜Φ+〉14、｜+〉2、｜+〉3，那么粒子6、8坍縮態（除歸一化因子）為

Bob引入2 個初態都為｜0〉的粒子A、B 并對粒子6進行單粒子測量，測量結果（除歸一化因子）為：

由上式可以看出如果測量結果為｜0〉6，隱形傳態直接失敗；如果測量結果為｜1〉6，隱形傳態可以繼續.Bob根據Alice 和Charlie 的測量結果對態｜ψ〉8AB（除歸一化因子）進行幺正變換并由表3 給出.

表3 對應粒子8、A、B的態Bob所實施的幺正變換Tab.3 UT of Bob corresponding to different states of 8，A and B

假定Charlie的測量結果為｜Φ+〉57，Alice的測量結果為｜Φ+〉14、｜+〉2、｜+〉3，Bob 的測量結果為｜1〉6，由表3可知，進行恒等變換后（除歸一化因子）為

接著，Bob以粒子8 為控制位，粒子A、B 為靶位分別作2 次CNOT操作，得到

然后，Bob引入初態為｜0〉的粒子C并且以基｛｜0000〉，｜1110〉，｜0001〉，｜1111〉｝8ABC進行U 變換，矩陣U由（11）式給出.其中，bi（i =1，2）的值依賴于粒子8、A、B、C的態.對于粒子8、A、B、C所處的態（除歸一化因子），矩陣元b1、b2的取值由表4 給出.

表4 粒子8，A、B、C的狀態及其對應的矩陣元b1、b2的值Tab.4 The state of particle 8，A，B and C corresponding to the value of the matrix element b1 and b2

對于態

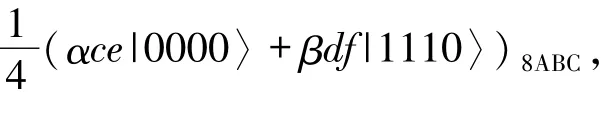
最后，Bob對粒子C進行測量，若測量結果為｜1〉C，則隱形傳態失敗；如果測量結果為｜0〉C，則隱形傳態成功且成功的概率為因此，方案2 的總成功概率為

3 結論

本文提出2種方案用于非最大糾纏GHZ態的受控量子隱形傳態.這2種方案相對于之前的GHZ態隱形傳態在可控性和安全性上都有一定的優點，同時也在保證成功率的情況下減少了一定的測量過程.本文的方案相比于文獻［10，13-14］有以下優點：

1）本文的信道中加有控制者，這一點大大提高了隱形傳態的安全性.

2）本文采用非最大糾纏的量子態作為信道，使得結論更具有一般性.

3）由文獻［12］知道W 態比較穩定，不易破壞，用W態作為信道可以提高安全性.方案2 以一個非最大糾纏的EPR對和一個非最大糾纏的W態為信道，較文獻［10 -11］中以2 個EPR 對作為糾纏信道隱形傳態過程更加安全.

本文與其他可控量子隱形傳態的不同在于，與文獻［7］中2 個四粒子GHZ態為信道相比，本文采用的量子信道為Bell 態和三粒子GHZ 態更易制備，從而節省了信道資源.本文相較文獻［11］在成功率相同的情況下，測量次數和幺正變換次數都有減少，這使得隱形傳態過程更簡便.相比文獻［12］，本文中發送者需征求控制者同意后，通過糾纏交換使發送者和接收者之間建立糾纏信道才可進行隱形傳態，因此安全性更進一步提高.