具有解析式正解的Stewart衍生型并聯機構的位移輸入協調關系

葉鵬達，尤晶晶,2*，沈惠平，吳洪濤，茹 煜

(1. 南京林業大學 機械電子工程學院，江蘇 南京 210037；2. 江蘇省精密與微細制造技術重點實驗室，江蘇 南京 210016；3. 常州大學 現代機構學研究中心，江蘇 常州 213016；4. 南京航空航天大學 機電學院，江蘇 南京 210016)

1 引 言

1965年，STEWART首次提出含6條相同支鏈的機構，學者們稱其為Stewart并聯機構[1]。相比于串聯機構，并聯機構具有輸出精度高、結構剛性好和承載能力強等優點，成為國內外機構學研究熱點[2-3]。目前，大多數6自由度并聯機構都是基于Stewart并聯機構衍生而來，我們稱之為Stewart衍生型并聯機構，其在光學元器件、并聯機床和六維加速度傳感器等領域得到越來越多的應用[4]。

然而，由于拓撲構型較復雜，6自由度并聯機構的精確實時控制一般很難實現。有研究發現[5-7]，基于并聯機構的裝置性能主要與其正向運動學問題有關。正向運動學的研究方法主要有解析法和數值法兩種[8-9]。解析法主要包括消元法、Grobner基法和共形幾何代數等方法。文獻[10]基于計算機符號運算，利用矢量消元和Sylvester結式消元，得出一般6-4臺體型Stewart并聯機構位置正解的一元32次方程；文獻[11]運用計算機代數系統中的分次字典序Grobner基算法，獲得一般6-6平臺型Stewart并聯機構位置正解的一元20次方程且該機構最多有40組解的結論；文獻[12]基于共形幾何代數建立運動學方程，并通過構造9階Sylvester結式，得到一般6-6臺體型Stewart并聯機構位置正解的一元40次方程。不難看出，這些方法最終都將并聯機構位置正解表達為一個一元高次代數方程，其優點是可以得到全部解，但消元和推導過程繁瑣，技巧性強，且計算量大，特別是針對臺體型Stewart并聯機構。數值法是另一種求解并聯機構正向運動學的方法，主要運用Newton-Raphson法(N-R法)等數值逼近迭代思路求解非線性方程組。文獻[13]針對6-6平臺型Stewart并聯機構提出了利用位置反解逐步迭代的方法求解位置正解的思路，保證了實時性，但每次只能迭代計算一組解；文獻[14]針對6-3 Stewart平臺結構提出了一種基于機構簡化的位置正解數值方法，保證了實時性，但對機構結構具有一定的依賴性。不難看出，并聯機構拓撲結構變得復雜時，數值法對于精確解的收斂性較差[15-17]。文獻[18]引入傳感器提高了模型算法的收斂性，但由于引入傳感器而造成結構上的復雜性，最終對算法的收斂性并沒有很大幫助。

考慮到并聯機構位置正解的求解難度與機構耦合度指標有關[19]，并且冗余驅動具有減少奇異位形和增加有效工作空間等優點[20]，文獻[21]提出了一種低耦合度冗余驅動Stewart衍生拓撲構型，由于尚未有與之相匹配的二重復合球鉸鏈，因而限制了其結構模型的設計。鑒于此，本文設計了二重復合球鉸鏈。除此之外，還設計了可轉換主動、從動模式的移動副，該移動副可用于改變機構的冗余度，實現變冗余驅動。

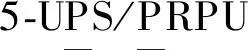
從以上分析可以看出，目前針對冗余驅動并聯機構的研究主要集中在機構內力協調，而對于移動副位移協調以及驅動模式優選方面的研究還較少，并且大多數研究的機構都是具有確定的冗余度，而對于變冗余度機構的研究相對較少。本文推導并化簡了6個位移輸入協調方程，為了便于對其進行驗證，重新推導出機構的位置正解；然后，分別運用N-R法和Broyden法求解了協調方程；進一步研究不同冗余度對冗余協調算法數值結果的影響；最后，總結出冗余驅動模式優選的3點選取原則。

2 結構模型及正向運動學

2.1 結構模型

圖1 Stewart衍生型并聯機構結構模型

Stewart衍生型并聯機構的結構模型和拓撲構型分別如圖1和圖2所示。該機構由1個邊長為2(n+L)的靜平臺、1個邊長為2n的動平臺、6個二重復合球鉸鏈、12個可轉換主動、從動模式的移動副和12個一般球鉸鏈組成。12個一般球鉸鏈與靜平臺相連，6個二重復合球鉸鏈與動平臺相連。初始狀態下，靜平臺與動平臺的中心重合，并且姿態相同。當驅動N(6≤N≤11)個移動副時，動平臺的位置和姿態發生變化，從而實現動平臺的六維運動。

圖2 Stewart衍生型并聯機構拓撲構型

如圖3所示，為了降低機構的耦合度，設計了一種二重復合球鉸鏈[25]，其主要由第一層鉸鏈、第二層鉸鏈和中心柱組成。第一層鉸鏈由第一套筒、內叉和第一滑柱組成，第二層鉸鏈由第二套筒、外叉和第二滑柱組成。中心柱與動平臺相連，滑柱與移動副相連，兩層鉸鏈均具有3條互相垂直的轉動軸線，并且轉動軸線始終相交于點Bi(i=1,2,...,6)。

如圖4所示，為了改變機構的冗余度，設計了一種可轉換主動、從動模式的移動副[26]，其主要由導桿、內套筒、外套筒和轉換套筒組成。導桿與內套筒之間滑動連接，內套筒與外套筒之間通過螺紋連接。當轉換套筒和導桿通過螺栓螺母連接在一起時，隨著內、外套筒之間發生相對轉動，移動副的長度也發生改變，此時，該移動副處于主動模式；當拆掉螺栓螺母時，導桿與轉換套筒分離，內套筒與導桿之間可相對滑動，此時，該移動副處于從動模式。

圖3 二重復合球鉸鏈結構模型

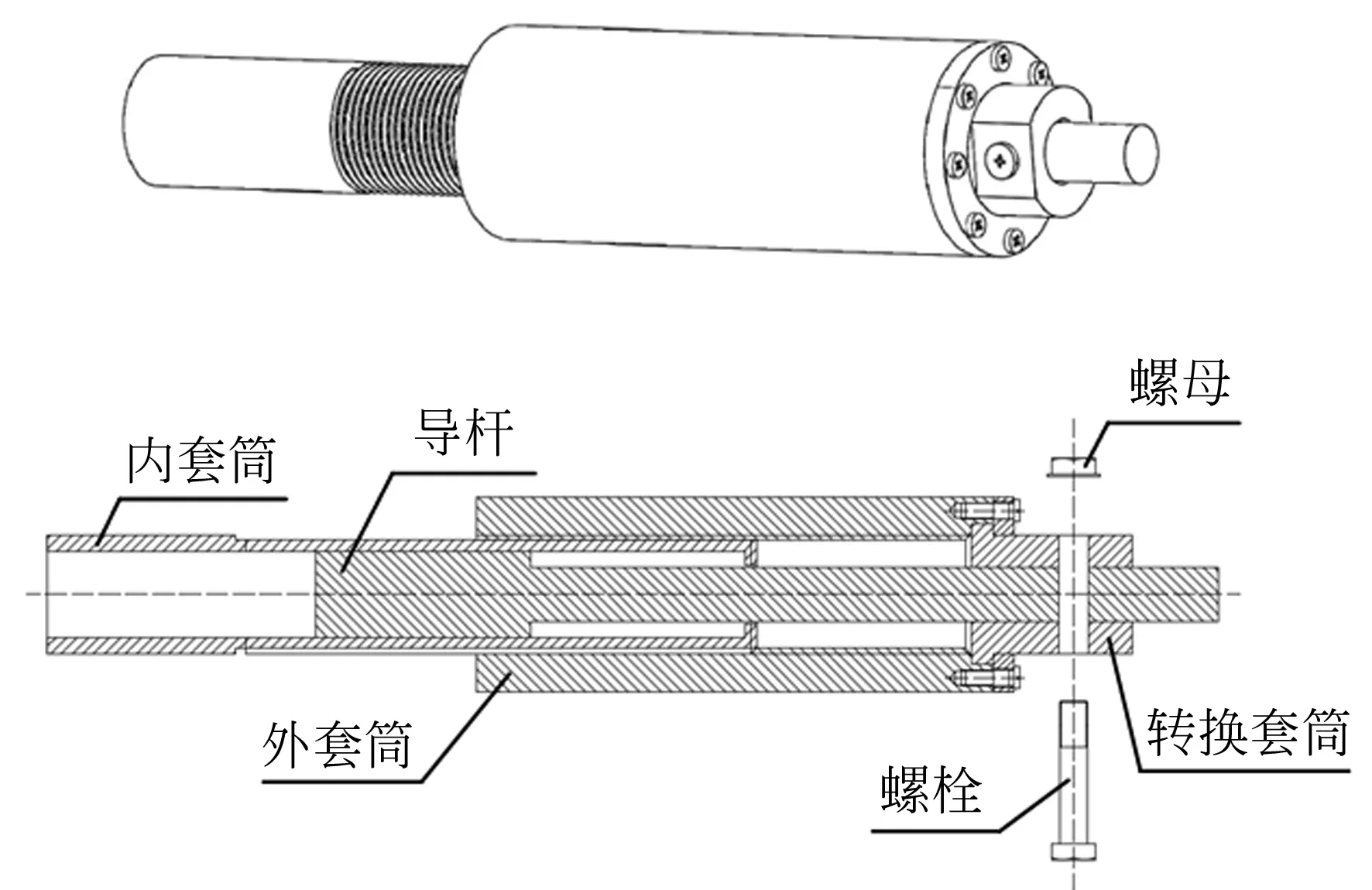
圖4 移動副的三維圖和剖面圖

2.2 正向運動學

并聯機構的正向運動學是指：已知驅動副的輸入量，求解動平臺的輸出運動參數。慣性坐標系{O-XYZ}與靜平臺相連，動坐標系{M-UVW}與動平臺相連，如圖2所示，慣性坐標系的坐標原點位于初始狀態下的動平臺中心處。12個一般球鉸鏈中心點在慣性坐標系中的笛卡爾坐標可表示成矩陣形式：

[b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12]=

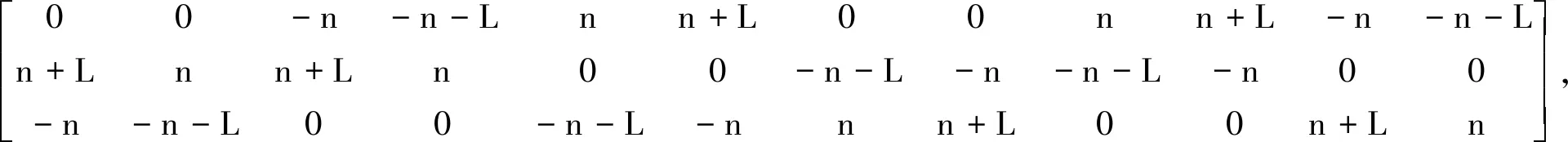
(1)

式中：b1～b12為同名點的幾何中心在慣性系內的笛卡爾坐標；n為動平臺半邊長；L為移動副初始長度。

12個移動副長度可表示為：

(2)

式中：Bi為同名點的幾何中心在慣性系內的笛卡爾坐標；|·|為矢量的模。

點M為動平臺的幾何中心，根據機構拓撲構型并且運用立體幾何知識可得出M點與Bi點之間滿足如下的關系：

B1+B4=B2+B5=B3+B6=2M，

(3)

B1+M=B2+B3，

(4)

(5)

為了便于計算，選取M，B1，B2和B34個點為待求量：

(6)

根據12個移動副的長度約束關系并結合式(5)，建立動平臺輸入、輸出量之間的位姿映射方程組。進一步分析后發現，同構方程兩兩相減，能夠消去二次項，得到4組線性封閉方程：

(7)

(8)

(9)

(10)

其中：

再結合式(4)，得到剩余3個未知量的解析式：

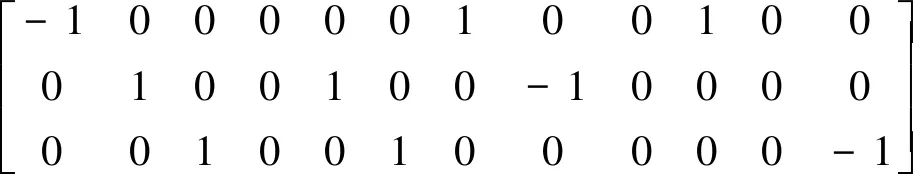
(11)

至此，重新推導了新型并聯機構的正向運動學，具體算法流程如圖5所示。

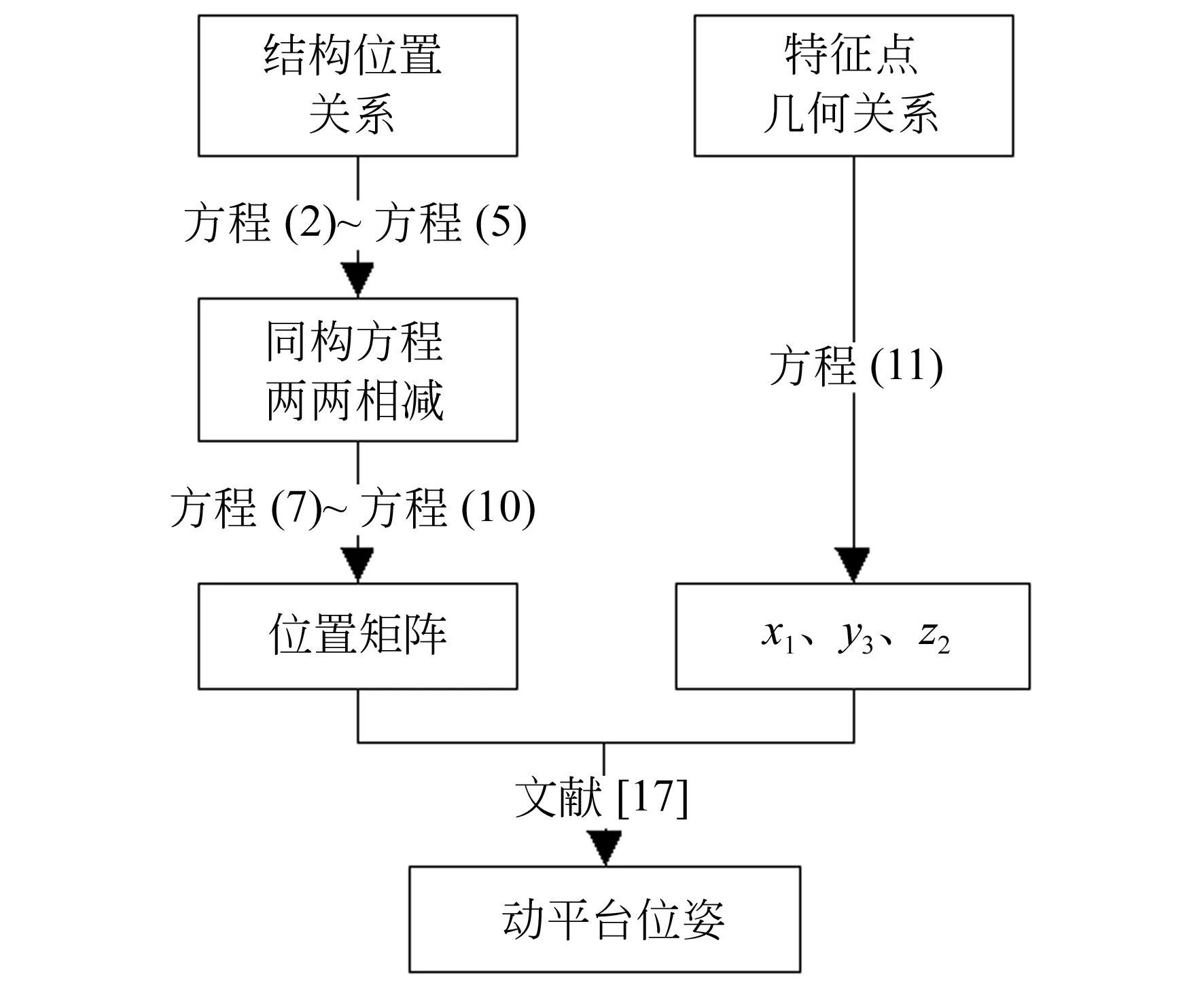
圖5 位姿正解算法流程圖

為了驗證位姿正解模型的正確性，在Mathematica中構建了Stewart衍生型并聯機構的虛擬樣機，如圖6所示。其中，動平臺半邊長n和移動副初始長度L分別設置為15 mm和25 mm。虛擬仿真中，動平臺為剛體，并且不考慮球面副、移動副的摩擦和間隙。不失一般性，取機構的初始狀態和任意狀態進行仿真，計算結果如表1所示。結果顯示，位姿正解的計算值與準確值完全一致。

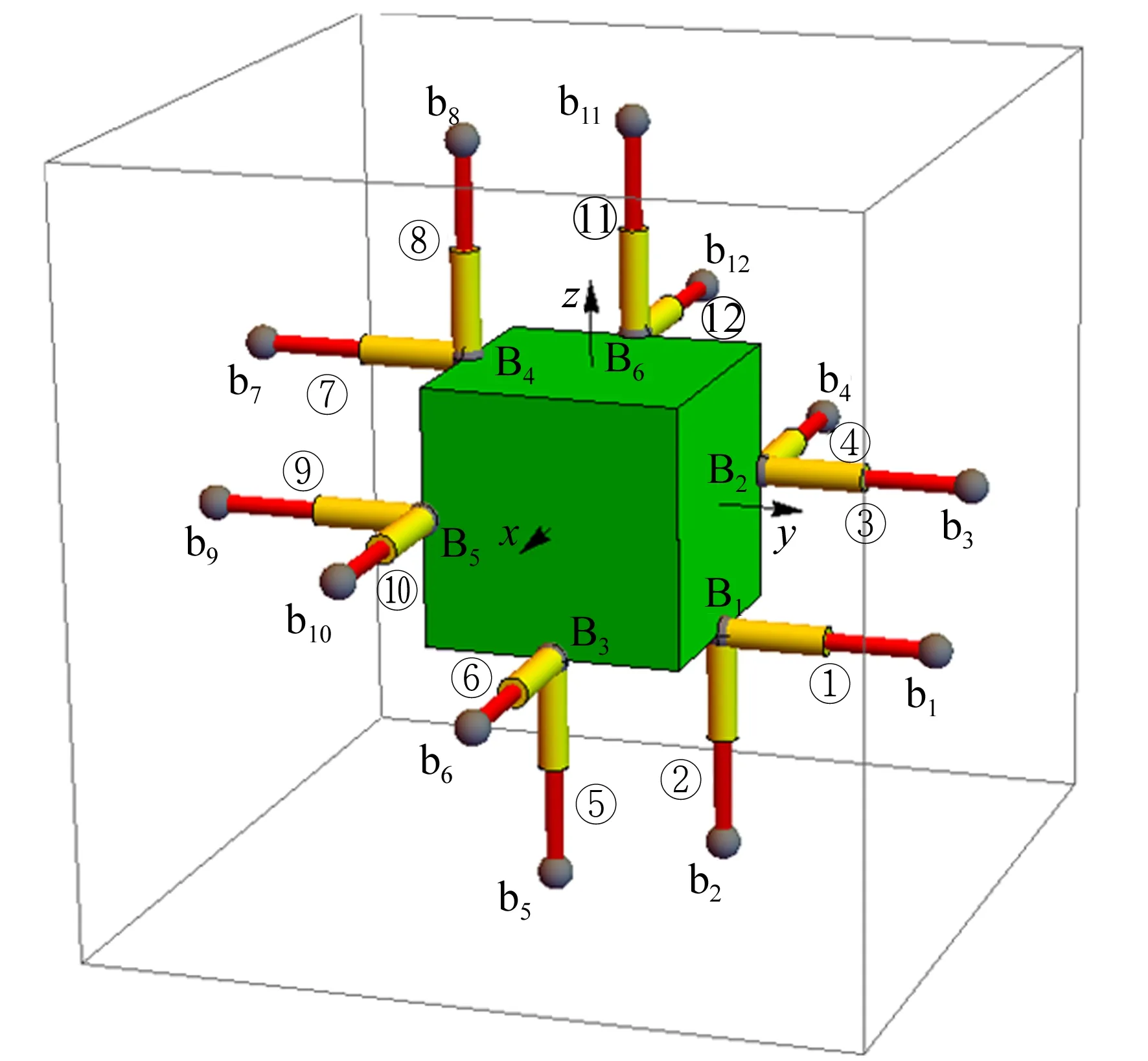
圖6 Stewart衍生型并聯機構的虛擬樣機

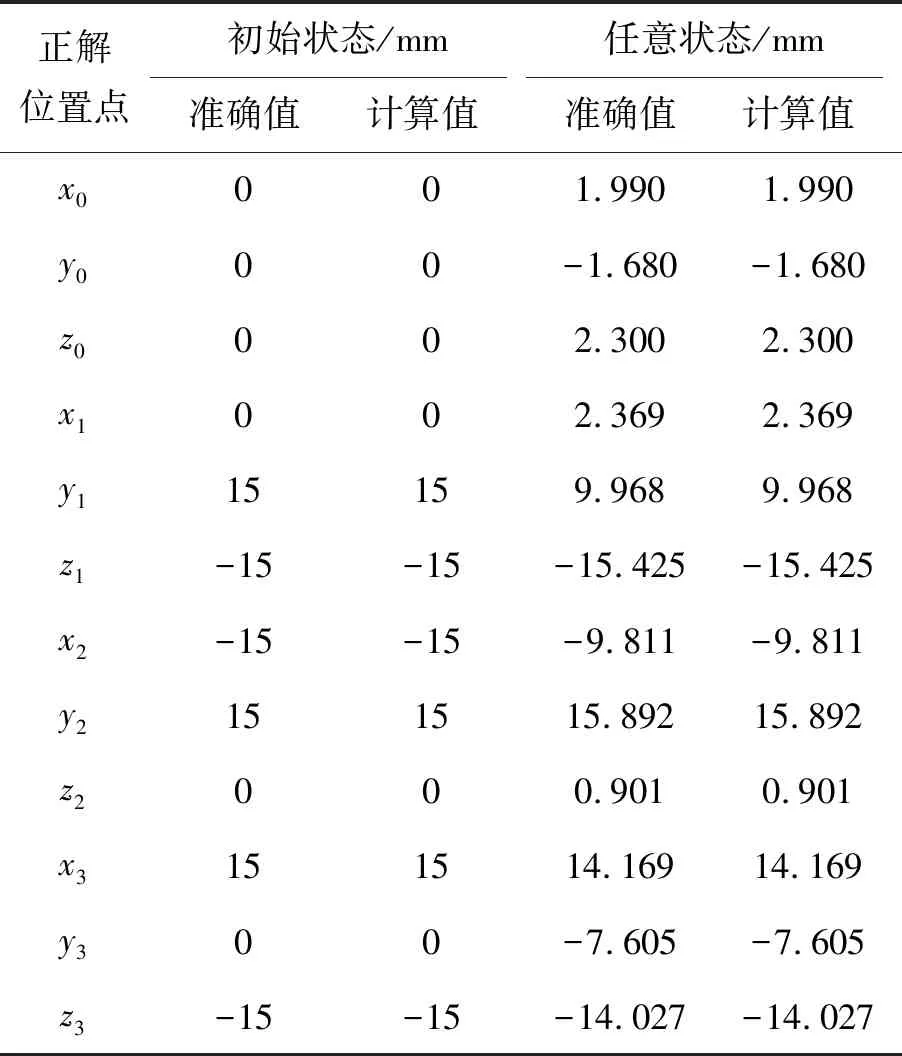
表1 位姿正解模型驗證

3 協調方程的推導及求解

3.1 協調方程的推導

將動平臺視作剛性結構，運動過程中位置點之間的相對距離保持不變。由并聯機構結構模型可知，移動副長度與位置點之間的尺度約束關系滿足如下關系式：

|B1-b1|2=x12+

[y1-(n+L)]2+(z1+n)2=l12，

(12)

|B2-b3|2=(x2+n)2+

[y2-(n+L)]2+z22=l32，

(13)

|B3-b5|2=(x3-n)2+

y32+[z3+(n+L)]2=l52，

(14)

|B1-M|2=(x1-x0)2+

(y1-y0)2+(z1-z0)2=2n2，

(15)

|B2-M|2=(x2-x0)2+

(y2-y0)2+(z2-z0)2=2n2，

(16)

|B3-M|2=(x3-x0)2+

(y3-y0)2+(z3-z0)2=2n2，

(17)

(18)

(19)

(20)

將式(7)～式(11)代入式(12)～式(20)，發現方程的最高次數達到8次，并且方程中所含高次項的項數也較多。為了降低方程的次數以及減少方程中高次項的項數，通過式(12)，式(15)相減、式(13)，式(16)相減、式(14)，式(17)相減、式(12)，式(13)，式(18)相減、式(13)，式(14)，式(19)相減、式(12)，式(14)，式(20)相減，得到如下6個位移輸入協調方程：

f(X)=2x1x0+2y1y0+2z1z0-x02-

y02-z02+3n2+(n+L)2-2y1(n+L)+

2z1n-l12=0,

(21)

g(X)=2x2x0+2y2y0+2z2z0-x02-

y02-z02+3n2+(n+L)2-2y2(n+L)+

2x2n-l32=0,

(22)

v(X)=2x3x0+2y3y0+2z3z0-x02-y02-

z02+3n2+(n+L)2+2z3(n+L)-

2x3n-l52=0,

(23)

u(X)=-2x1x2-2y1y2-2z1z2-2x2n+

2y2(n+L)-2n2-2(n+L)2+

2y1(n+L)-2z1n-(2n2-l12-l32)=0,

(24)

w(X)=-2x2x3-2y2y3-2z2z3-2x2n+

2y2(n+L)-2n2-2(n+L)2-

2z3(n+L)+2x3n-(6n2-l32-l52)=0,

(25)

h(X)=-2x1x3-2y1y3-2z1z3-2z3(n+L)+

2x3n-2n2-2(n+L)2+2y1(n+L)-

2z1n-(2n2-l12-l52)=0.

(26)

將式(7)～式(11)代入式(21)～式(26)可知，消除了式(21)、式(22)、式(23)中的8次方項以及式(24)、式(25)、式(26)中的6次方項。化簡前后的協調方程對比如表2所示。

表2 化簡前后的協調方程對比

Tab.2 Comparison of the compatibility equations before and after simplification

方程特征項化簡前化簡后數目96最高次數88最高次項數459

為了驗證協調方程的正確性，并聯機構結構參數與2.2節中的參數一致，在Mathematica中仿真對比了6個協調方程在兩種不同狀態下的計算結果。表3列出了兩種狀態下協調方程的計算誤差，將6個協調方程誤差的平均值作為綜合誤差。誤差δ的表達式為：

δ=|F(X)*-F(X)*|,

(27)

其中：

F(X)=

式中：上標“*”代表仿真結果；下標“*”代表準確結果；X為從動副長度。

由表3可知，當移動副位于初始狀態時，計算結果沒有產生誤差；當移動副位于任意狀態時，計算結果產生較小誤差，該誤差可能是由計算機浮點運算中的舍入誤差和泰勒展開時的截斷誤差等因素造成，可以忽略不計。計算結果表明協調方程推導正確。

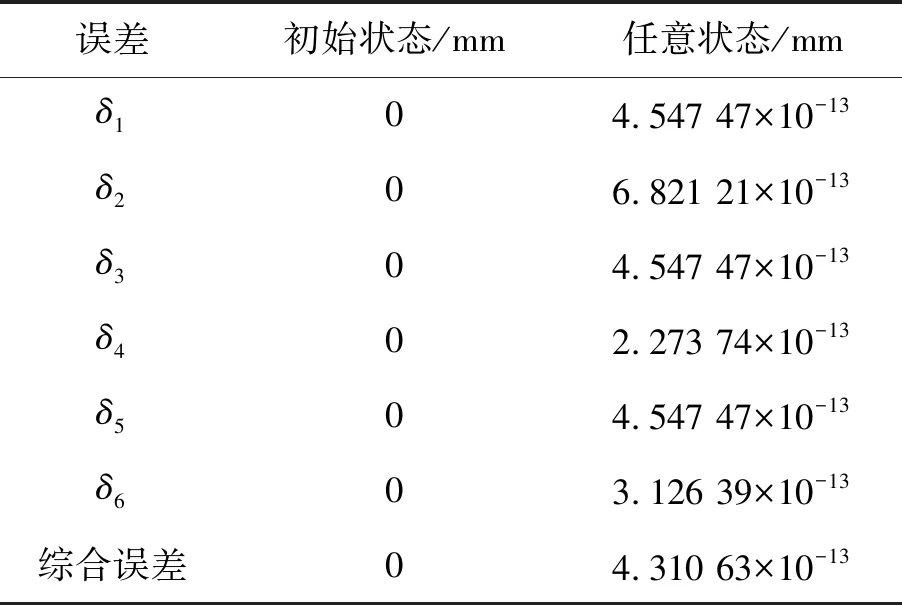
表3 協調方程的誤差統計

3.2 協調方程的求解

并聯機構12個移動副之間滿足一定的位移輸入協調關系，由于協調方程的次數均高于4次，給定N個驅動副長度，可通過數值方法計算出其它(12-N)個從動副長度。求解非線性方程組的數值方法主要包括不動點迭代法、牛頓法和擬Newton法等方法，本文選擇其中的N-R法和Broyden法進行求解，其它方法將另文研究。

3.2.1 N-R法

N-R法是求解非線性方程組的經典方法，因其收斂速度快和自校正等優點，得到了廣泛的應用。目前很多新的算法都是在此基礎上改進而來。

協調方程可以表示為：

F(X)=0.

(28)

泰勒公式展開：

F(Xk)+

F′(Xk)(Xk+1-Xk)+O(|Xk+1-Xk|2)=0,

(29)

其中：

式中：k為迭代步數；F′(Xk)為Jacobian矩陣。

忽略二階無窮小量可得到：

Xk+1=Xk-[F′(Xk)]-1F(Xk).

(30)

式(30)即為N-R法的迭代公式。N-R法是局部收斂的，只要初值選取得當，計算結果總能收斂到合理值。N-R法求解協調方程的算法流程如圖7中實線所示。

3.2.2 Broyden法

Broyden法是基于改進的N-R法發展而來，是求解非線性方程組的重要方法之一。它克服了N-R法需要求導、求逆等缺點，將Jacobian矩陣簡化為矩陣遞推關系式，這樣不僅簡化了計算過程，同時還能保證方法的超線性收斂速度[27]。當然，在改進的N-R法成立的前提下，Broyden法是計算修正矩陣ΔAk的一種方法，其它方法還包括Broyden第二方法、DFP秩2算法和BFGS秩2算法等。

Broyden首先對改進的N-R法提出了一種修正Ak的計算方案，它每步迭代只需計算n個分量函數值及O(n2)次算術運算，大大降低了計算量，其迭代公式為：

(31)

其中：

Sk=Xk+1-Xk

yk=F(Xk+1)-F(Xk).

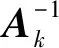
(32)

式中：SkTBkyk≠0。逆Broyden秩1公式每步總計算量為n個分量函數值和O(n2)次算術運算。

式(32)即為Broyden法的迭代公式。Broyden法求解協調方程的算法流程如圖7中虛線所示。

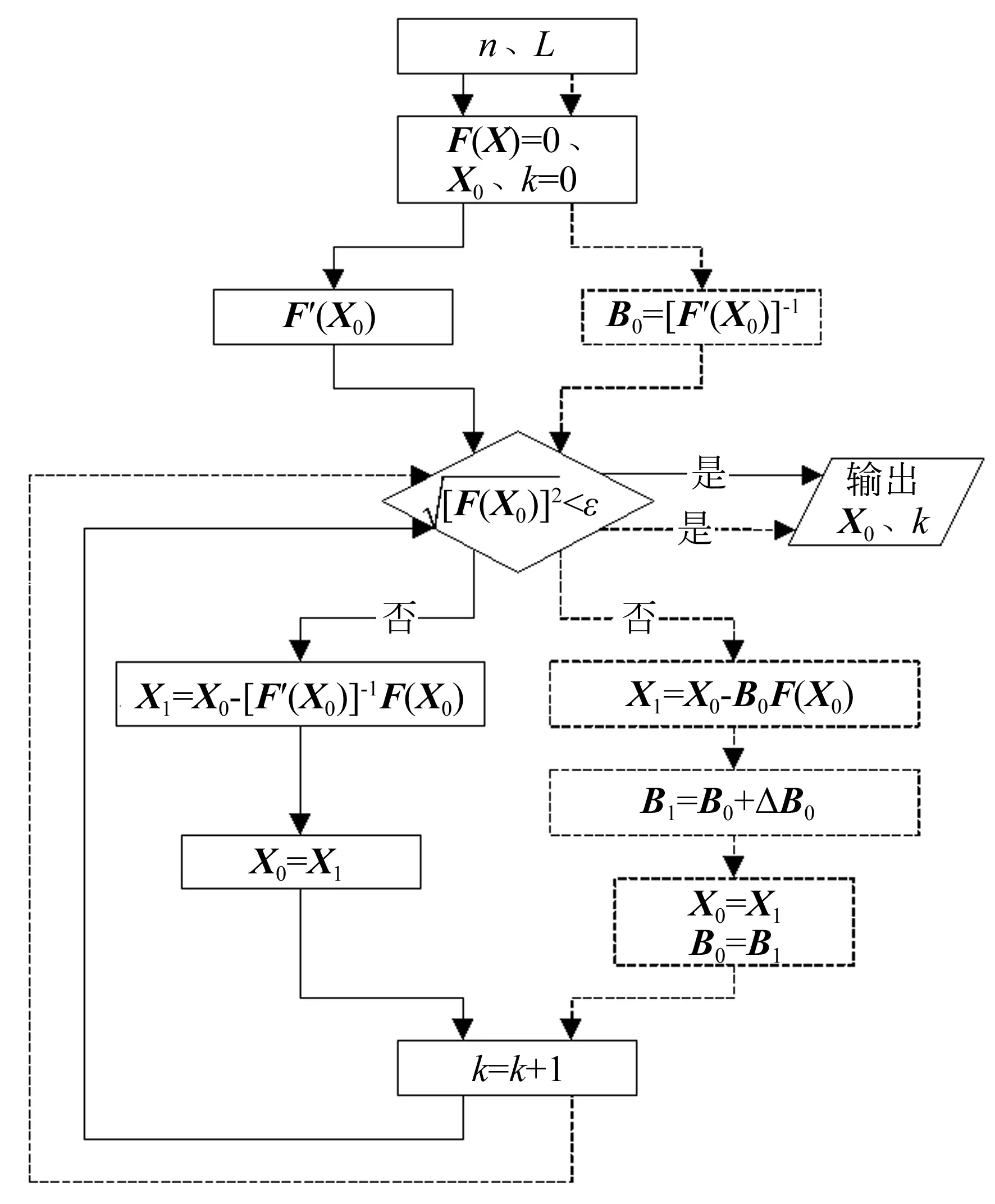
圖7 兩種迭代算法流程圖

觀察圖7可以發現，與N-R法相比，Broyden法在迭代過程中不需要計算Jacobian矩陣，而是用當前函數值代替導數，避免了每次迭代過程中的求導，降低了計算量。

為了對比數值結果的精度和效率，將兩種算法編寫成Mathematica程序，并在軟件中通過Timing指令獲取算法的計算時間。不失一般性，任意給定動平臺一組位姿：x0=0.5 mm，y0=0 mm，z0=0 mm；λ1=-0.05，λ2=0.05，λ3=0.05，迭代精度控制為1.0×10-6，仿真結果如表4所示。表5列出了許可初值偏差從20%變化到25%時，計算結果收斂到給定位姿所運行的迭代步數和計算時間。

表4 協調方程數值結果精度對比

表5 協調方程數值結果效率對比

Tab.5 Efficiency comparison of numerical results of the compatibility equations

許可初值偏差/%N-R迭代步數時間/msBroyden迭代步數時間/ms205187.510156.3215203.110156.3225203.111156.3235203.111156.3246218.811171.9256250.012187.5平均值5.3210.910.8164.1

觀察并分析表4，5可知， N-R法數值結果的精度優于Broyden法至少3倍，但效率較低。從迭代步數和計算時間可以看出，在相同許可初值偏差情況下，雖然Broyden法收斂到滿足精度要求的給定位姿所運行的迭代步數較多，但由于每一步迭代不需要構造Jacobian矩陣，因此計算量較少，計算時間僅為N-R法的78%左右。

將兩種算法的許可初值偏差均取為30%，其迭代收斂性如圖8所示，其中綜合桿長表示計算桿長的平均值。為了更清晰地反映兩種算法的收斂性，選取圖中計算值與準確值較接近的部分曲線進行局部放大。從圖8中可以看出，使用Broyden法計算得到的桿長收斂曲線圍繞準確值的擾動較小，并且在迭代步數達到4步時，計算值與準確值基本吻合。因此，Broyden法的收斂速度較快，即收斂性較優。

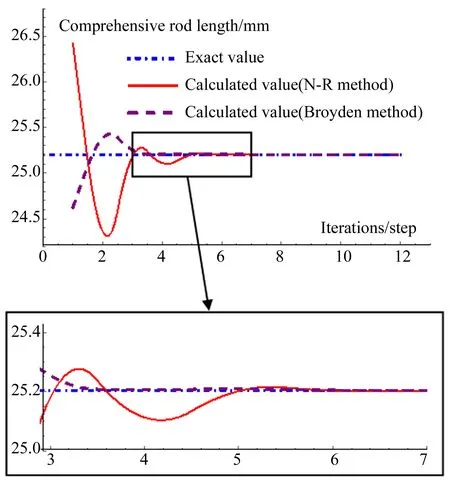
圖8 兩種迭代算法的收斂性

4 協調方程數值結果的影響因素

通過切換移動副的工作模式，從而改變機構的冗余度，實現6種驅動模式，如圖9所示，其中R代表機構的冗余度。協調方程數值結果的影響因素主要包括許可初值偏差和并聯機構結構參數，針對各種驅動模式，分別對比分析這兩者對冗余協調算法的影響。

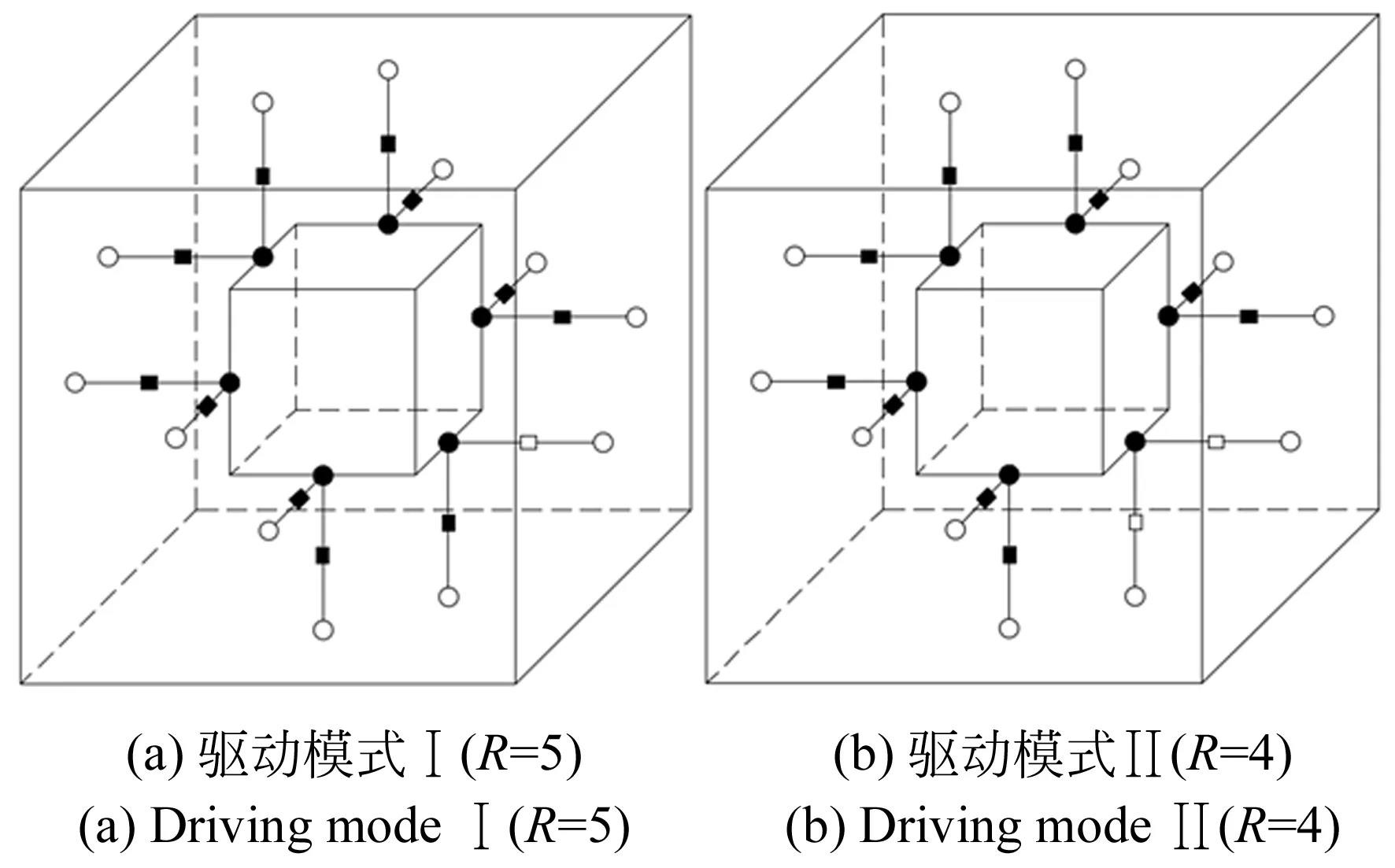
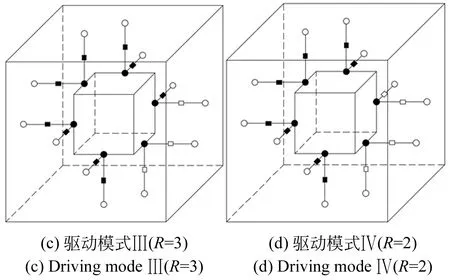
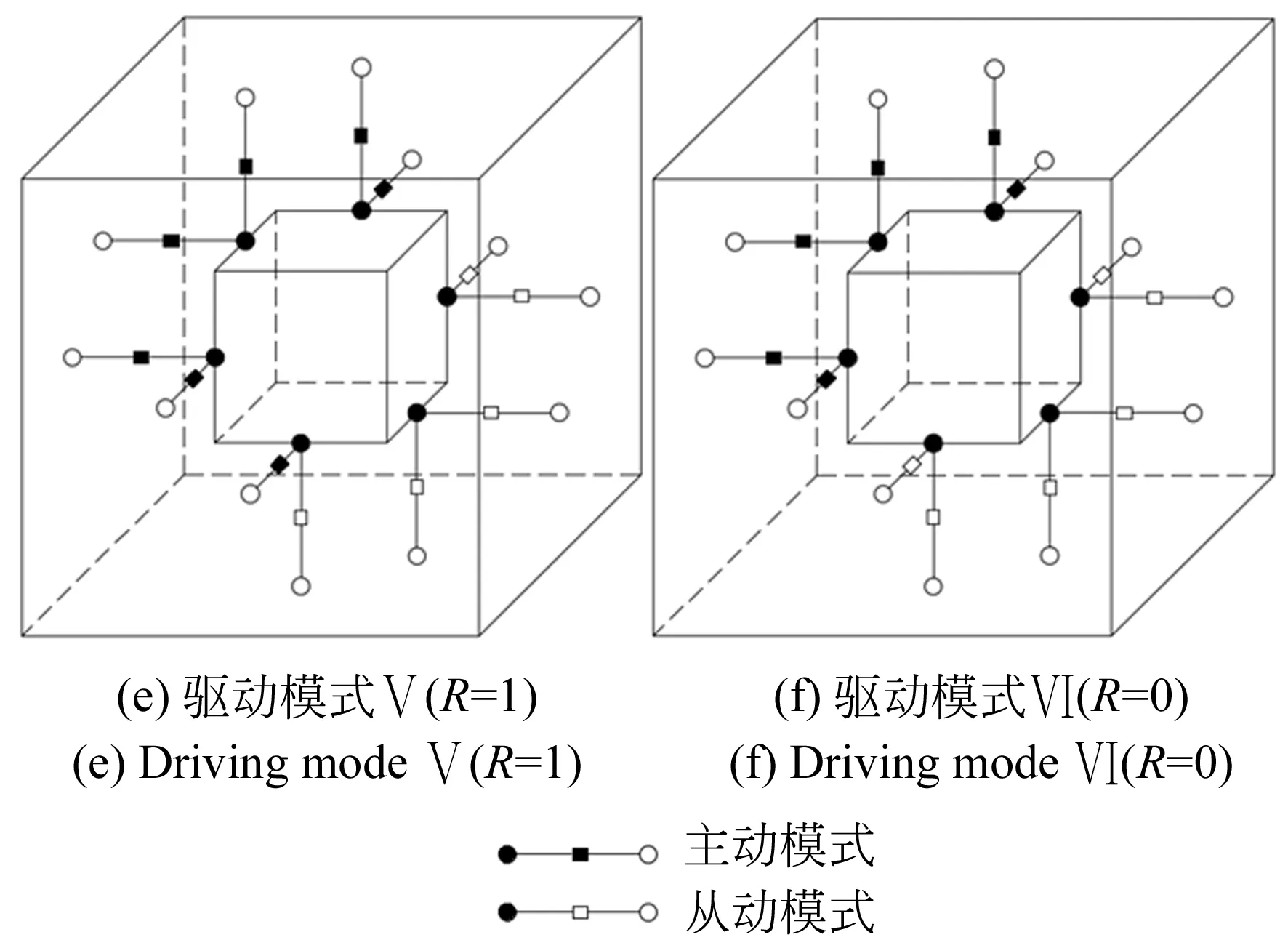
圖9 6種驅動模式

4.1 許可初值偏差

N-R法和Broyden法在計算協調方程時都需要給定算法迭代初值，如果初值選取不當，就會造成計算結果發散，失去有效性。并聯機構結構參數與2.2節中的參數一致，分別給定算法迭代精度為1.0×10-6與1.0×10-9，仿真結果如圖10和圖11所示。本文以一組結構參數為例，給出了確定最佳冗余度的方法和思路，為類似并聯機構驅動模式的選取提供參考。

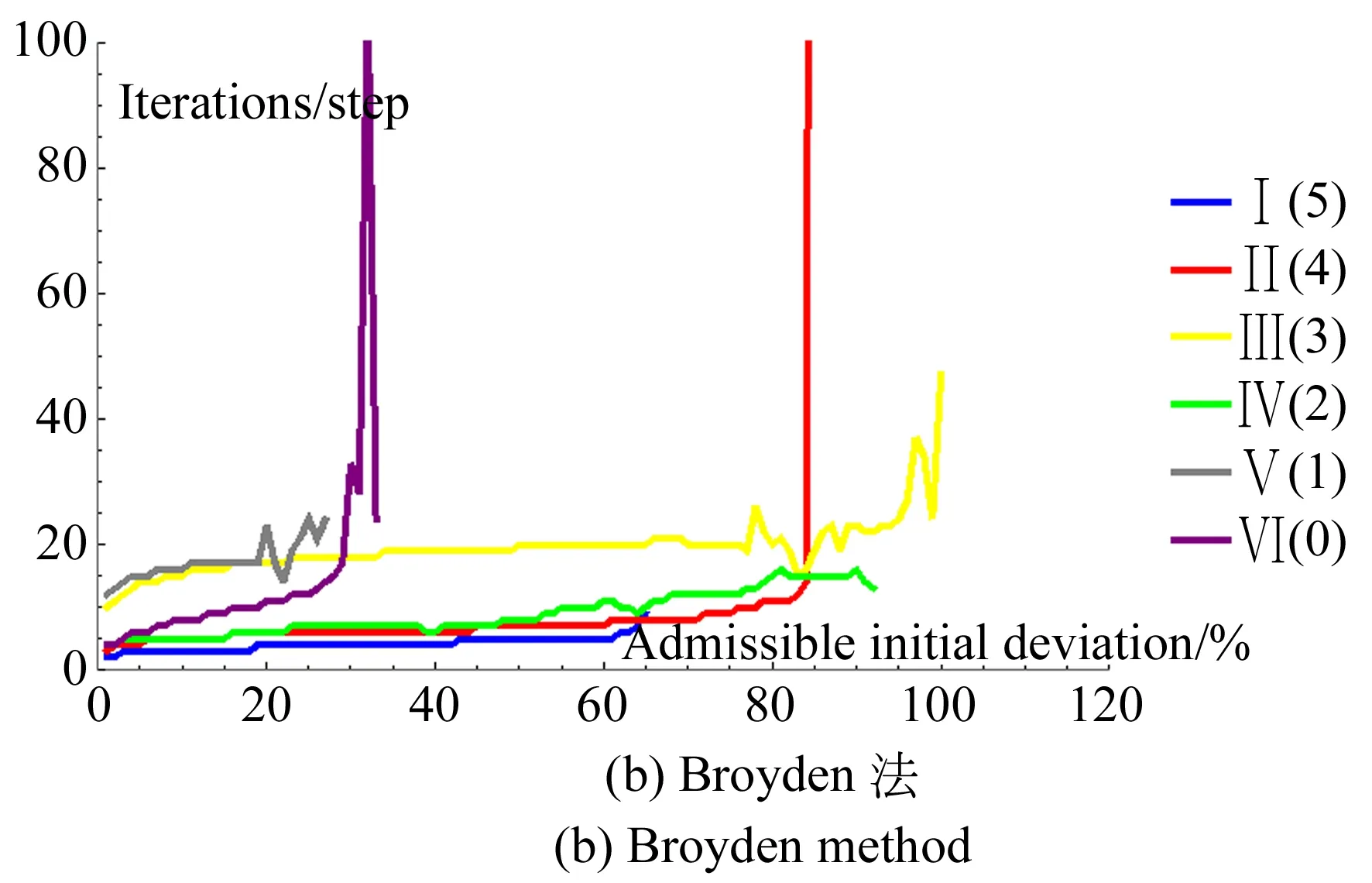
圖10 許可初值偏差與迭代步數的關系(1.0×10-6)

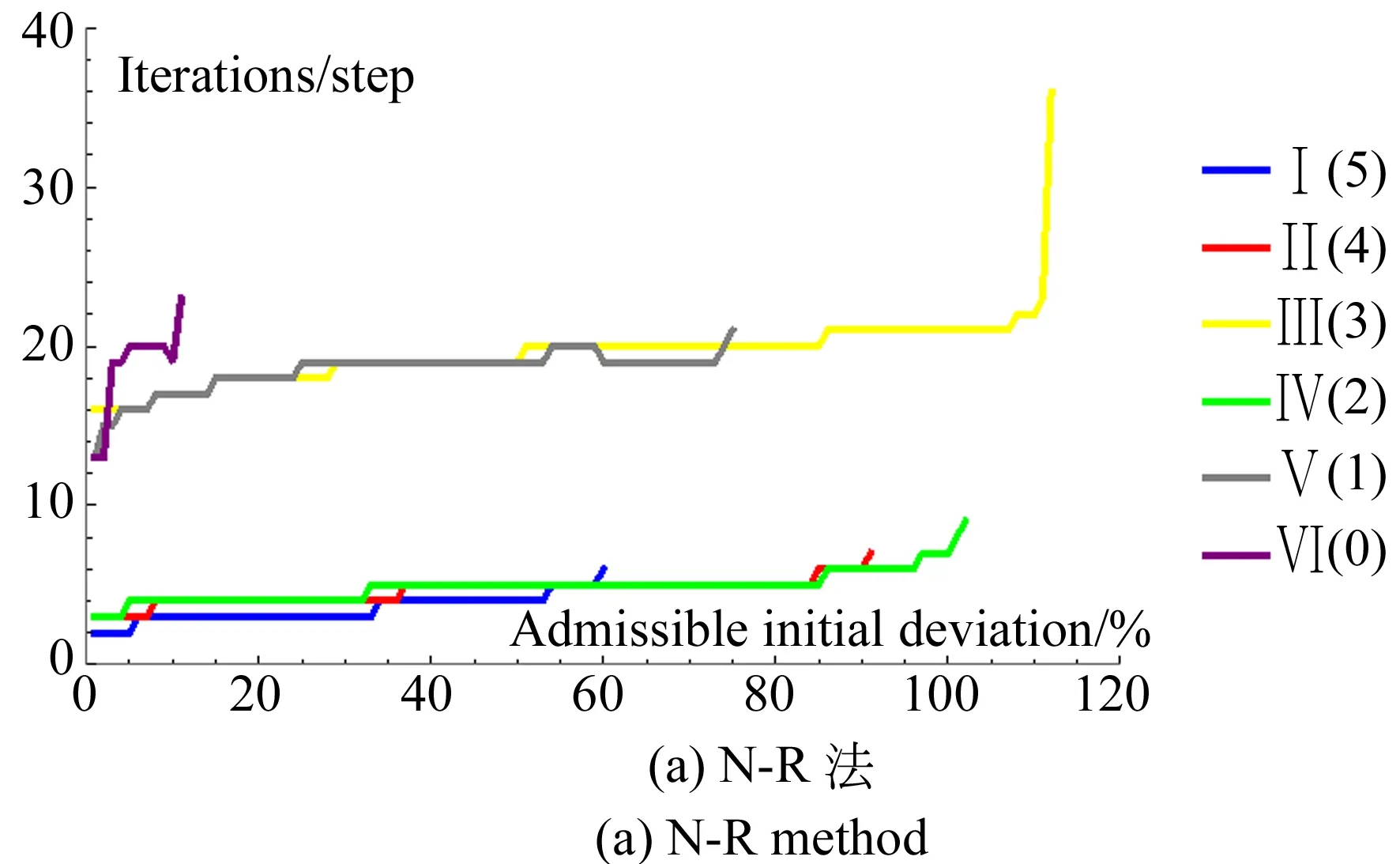
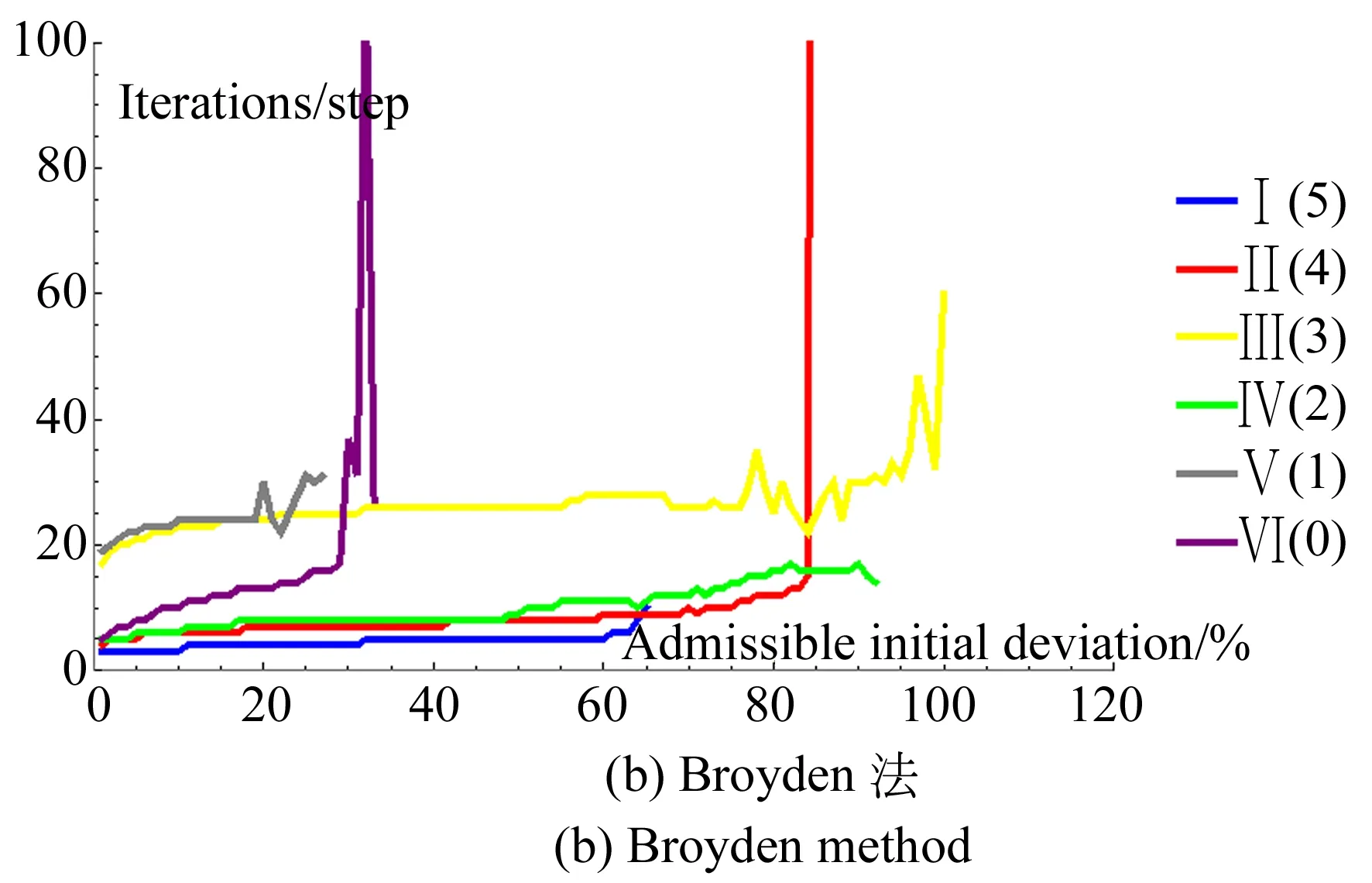
圖11 許可初值偏差與迭代步數的關系(1.0×10-9)

觀察并分析圖10和圖11可知：

(1)隨著許可初值偏差的增大和迭代精度的提高，迭代步數呈上升趨勢。R=3時，冗余協調算法對初值的依賴程度較低；R=1時，Broyden法對初值的依賴程度較高；R=5時，迭代步數都較低，即實時性較優。

(2)冗余度為0，1，3時，迭代步數對迭代精度的敏感程度都較高；特別地，對于N-R法，當R=0時，迭代步數對迭代精度較敏感，并且對許可初值偏差的要求較高，究其原因，這可能是由于Jacobian矩陣維數的增加導致計算量變大，以及更易產生奇異等原因造成的。

(3)隨著許可初值偏差的增大，N-R法的迭代步數變化較平緩，即穩定性較優，而對于Broyden法，當許可初值偏差接近最大許可初值偏差時，迭代步數產生較大波動，從波動的整個趨勢來看，呈上升態勢。

4.2 結構參數

對于不同的驅動模式，冗余協調算法的最大許可初值偏差與并聯機構結構參數有關。不失一般性，取5～30 mm分別作為動平臺半邊長和移動副初始長度的變化范圍，均以5 mm作為變化步長，依次獲取每種結構參數所對應的最大許可初值偏差，仿真結果如圖12所示。其中黃色代表N-R法，藍色代表Broyden法。

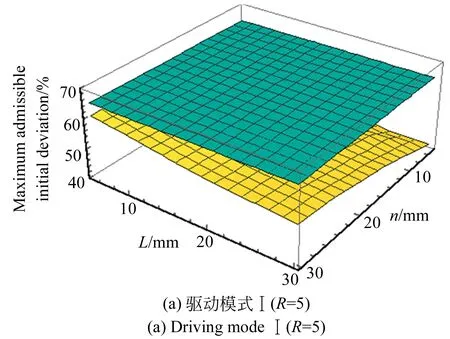
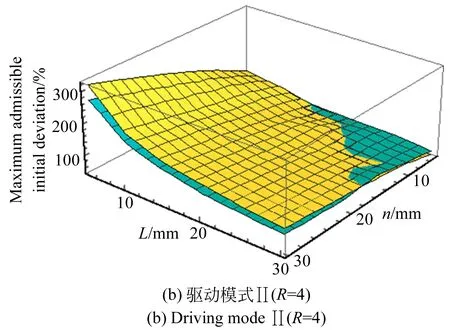
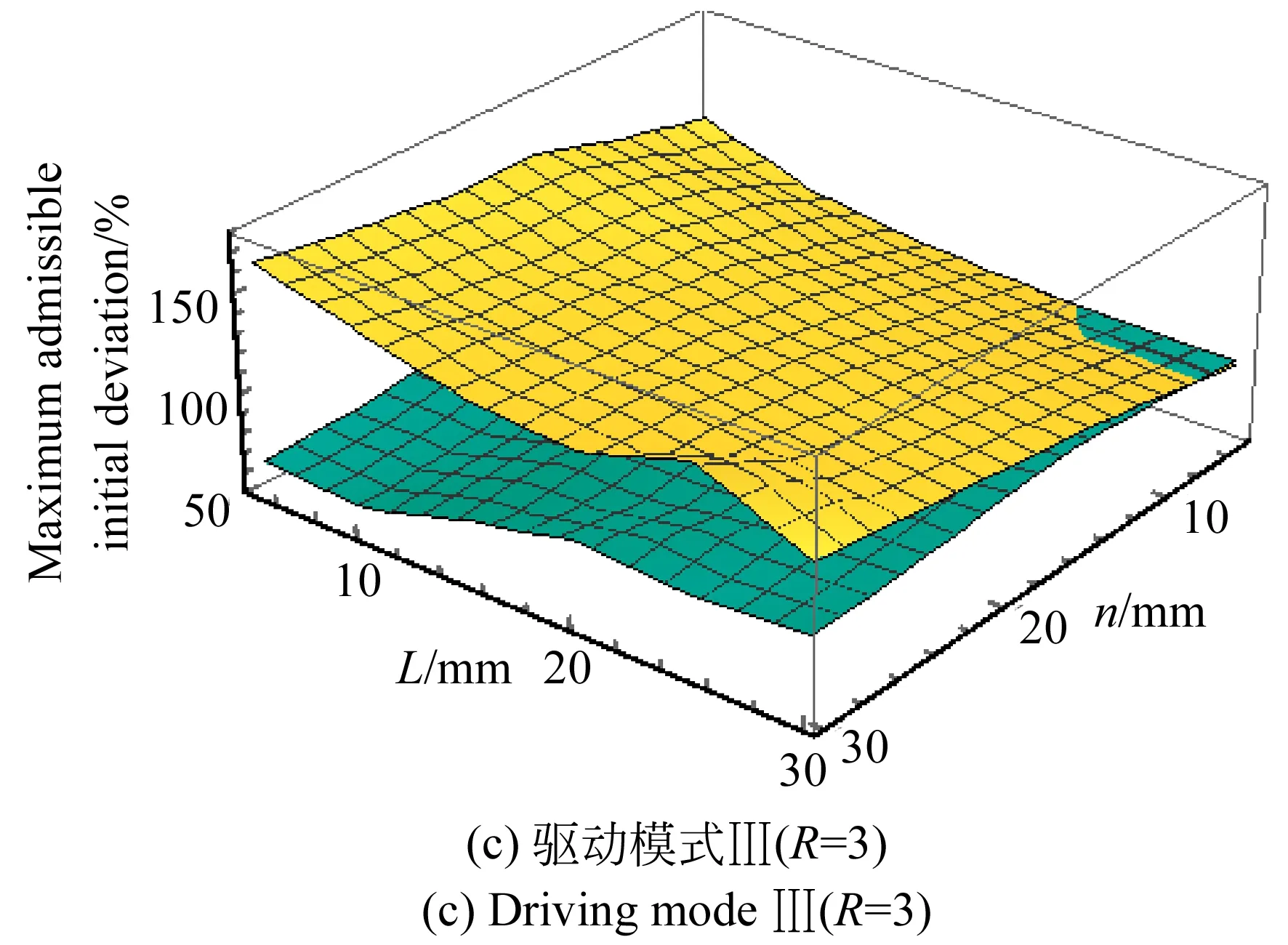
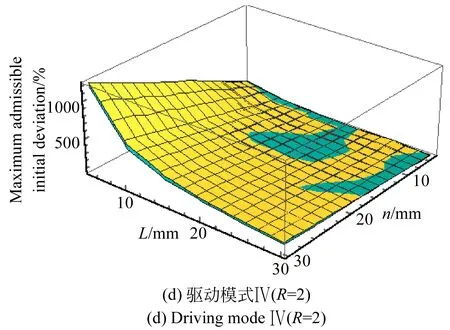
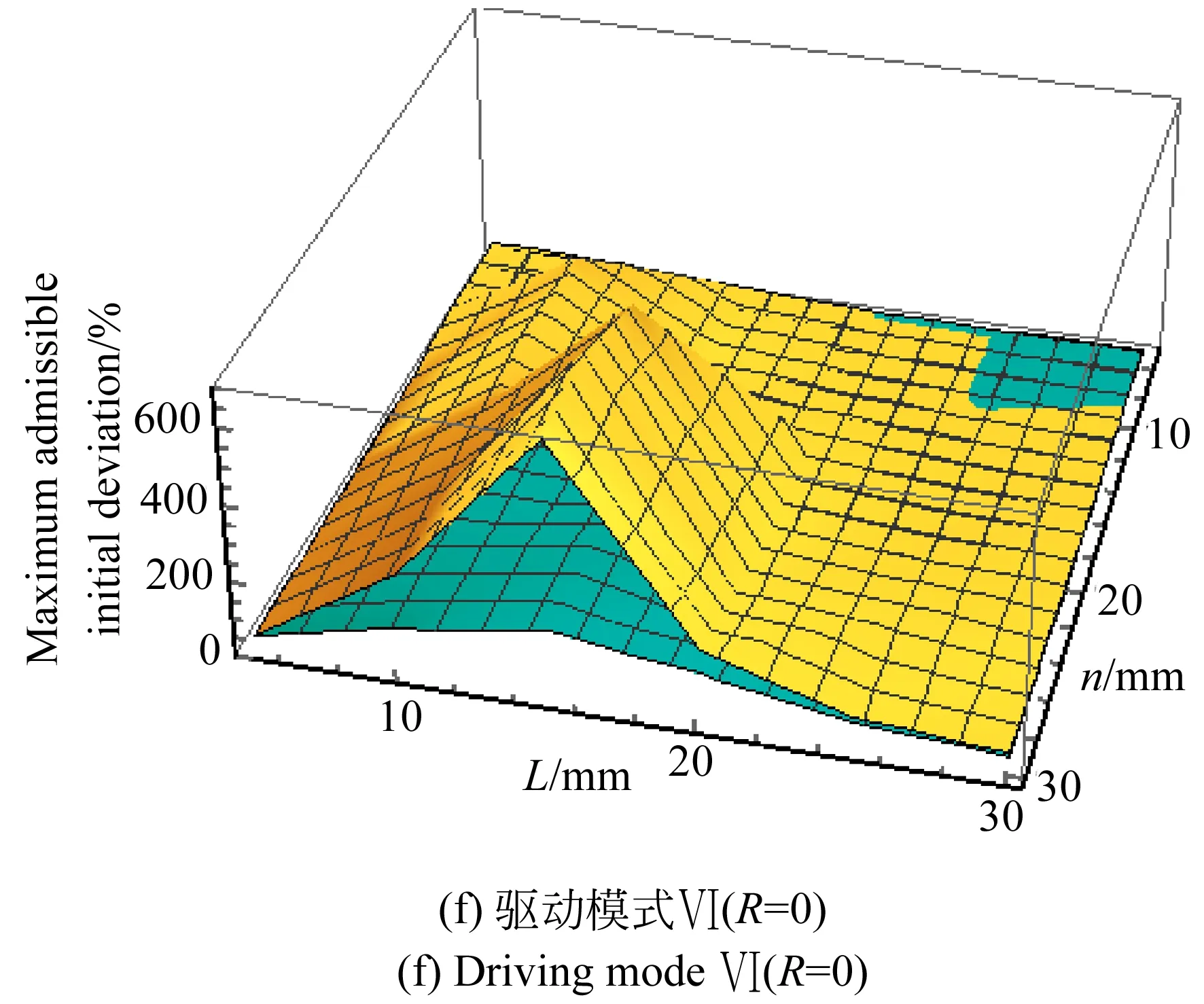
圖12 結構參數與最大許可初值偏差的關系

Fig.12 Relation ship between structural parameters and maximum admissible initial deviation

觀察并分析圖12可知：

(1)從整體趨勢來看，隨著動平臺邊長的增大和移動副初始長度的減小，最大許可初值偏差呈上升趨勢。

(2)R=5時，最大許可初值偏差的區間寬度都較小，分別為19%和0%，此時，最大許可初值偏差對結構參數變化的敏感程度較低；R=2時，最大許可初值偏差的區間寬度都較大，分別為1 218%和1 174%，此時，最大許可初值偏差對結構參數變化的敏感程度較高，即在該驅動模式下，通過合理選取結構參數，能夠增大冗余協調算法的最大許可初值偏差。

(3)R=0時，最大許可初值偏差在移動副初始長度為15 mm左右出現凸峰，究其原因，這可能是由于算法在計算Jacobian矩陣時較易產生奇異所導致。

為了進一步定量地對比驅動模式對冗余協調算法產生的影響，運用區間分析理論，引入并定義擾動適應性能評價指標，將6種驅動模式下的擾動適應性能的平均值作為對應算法的綜合擾動適應性能。擾動適應性能的表達式為：

(33)

顯然，擾動適應性能P值越小，表明冗余協調算法的抗擾動性能越強。表6列出了不同驅動模式下冗余協調算法的擾動適應性能。

表6 冗余協調算法的擾動適應性能對比

Tab.6 Comparison of perturbation adaptive performance of redundant coordination algorithm

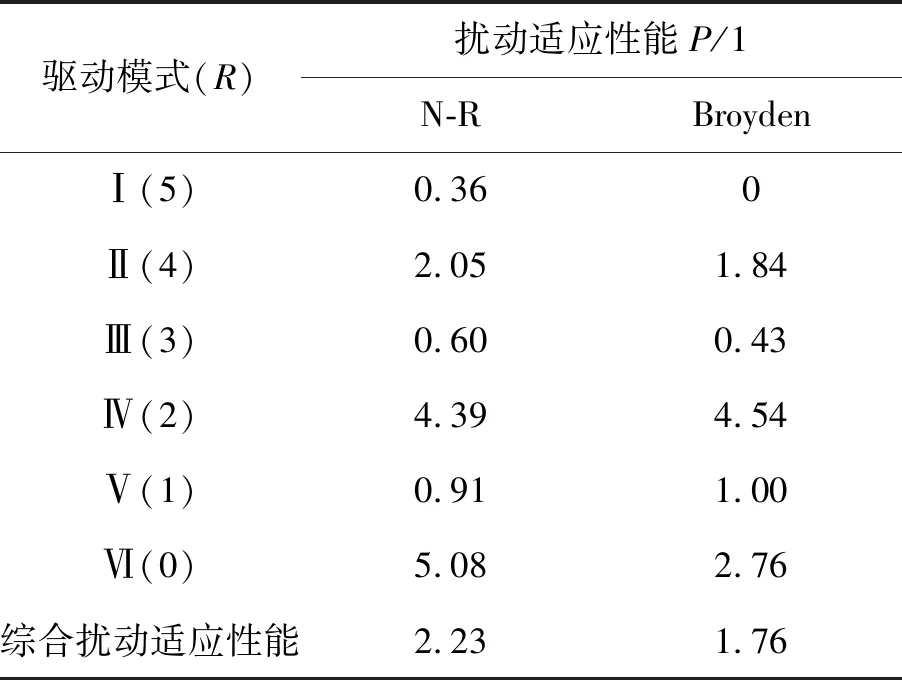
驅動模式(R)擾動適應性能P/1N-RBroydenⅠ(5)0.360Ⅱ(4)2.051.84Ⅲ(3)0.600.43Ⅳ(2)4.394.54Ⅴ(1)0.911.00Ⅵ(0)5.082.76綜合擾動適應性能2.231.76

觀察并分析表6可知：

(1)冗余度為1，3，5時，冗余協調算法的抗擾動性能較強，即最大許可初值偏差對結構參數變化的敏感程度較低，從移動副的布局方式來看，冗余度為奇數時，至少存在1個二重復合球鉸鏈，其兩端連接的移動副由驅動副和從動副混連構成，該構成形式能夠實現冗余協調算法的擾動補償。

(2)特別地，當R=5時，Broyden法的擾動適應性能為0，在該驅動模式下，結構參數的變化對最大許可初值偏差不產生影響。從綜合擾動適應性能來看，Broyden法優于N-R法1.27倍，即Broyden法的抗擾動性能較優。

5 結 論

以具有解析式正解的Stewart衍生拓撲構型為研究對象，為了降低機構的耦合度，發明了一種二重復合球鉸鏈，還給出了可轉換主動、從動模式的移動副的一種設計方案，該移動副可以改變機構的冗余度，從而實現驅動模式的切換。構造了位置正解全解析算法，并驗證了位置正解模型的正確性，該方法同樣適用于動平臺上含3個以上二重復合球面副、球鉸中心不局限于動平臺棱邊中點且耦合度小于2的臺體型并聯機構位置正解的求解。

根據位置點之間的幾何關系推導并化簡了6個位移輸入協調方程，分別對比分析了N-R法和Broyden法的數值性態，研究發現，N-R法的精度優于Broyden法至少3倍，Broyden法的計算時間約為N-R法的78%，Broyden法的綜合擾動適應性能優于N-R法的1.27倍。同時，研究了許可初值偏差和結構參數對冗余協調算法的影響。

Stewart衍生型并聯機構在具體應用場合需要合理選取驅動模式，其選取原則為：要允許有較大的最大許可初值偏差時，最佳冗余度為3；要使最大許可初值偏差對結構參數變化較敏感時，最佳冗余度為2；對實時性和抗擾動性能要求較高時，最佳冗余度為5。

本文僅討論了N-R法和Broyden法的數值性態，對于其他算法是否會得到不同結論，該問題將另文研究。