基于Pride巖石骨架模型的橫波孔隙度計算方法*

李志愿

(中海石油(中國)有限公司天津分公司 天津 300459)

不同的巖石骨架模型分別從各自的角度建立了巖石骨架與巖石基質之間的關系。Nur等[1]通過定義臨界孔隙度，認為巖石骨架的剪切模量與孔隙度之間存在線性關系。Pride等[2]則通過引入固結系數，認為巖石骨架的剪切模量與巖石孔隙度以及固結系數有關，而固結系數則取決于巖石所受到的有效壓力和巖石的孔隙結構。之后，Lee[3]又對Pride模型進行了改進，本文將這兩種理論統稱為Pride模型。張佳佳 等[4]通過對不同巖石骨架模型的對比認為，相比于Nur模型，Pride模型對于中低孔隙度儲層有更好的效果，適用性更廣。

海上油田在勘探評價階段，探井、評價井通常采用電纜測井系列，測井曲線齊全。但由于環境因素的影響，油田開發過程中，中子、密度測井的應用受到較大限制。聲波測井因具有無放射源、節約鉆時，并且能夠獲得縱、橫波時差等優勢，在開發井中的應用越來越廣泛。聲波測井不僅可以測量地層的縱波，也可以在軟地層中進行偶極子波測量，獲得質量較高的橫波數據，從而為利用橫波計算孔隙度提供了有利條件[5]。王建強 等[6]建立了基于Nur模型的橫波時差孔隙度計算方法，但該方法在中低孔隙度儲層并不適合。本文基于Pride巖石骨架模型，結合Biot-Gassmann理論以及巖石體積物理模型建立的橫波孔隙度計算方法適用于中低孔隙度儲層，適用范圍更廣，且應用效果更好。

1 理論分析與數學推導

在地震巖石物理中，Biot-Gassmann理論通常用來描述地震響應與巖石物性之間的關系，但是該理論并沒有闡述巖石骨架和巖石基質之間的關系。為了能夠有效地建立二者之間的關系，出現了各種各樣的巖石骨架模型，如Nur模型和Pride模型等，分別從不同的角度闡述了多孔巖石的骨架與基質之間的關系。巖石骨架模型的出現使得聲波與儲層物性、巖石骨架及巖石基質之間建立起了聯系，為利用橫波計算孔隙度提供了理論基礎。同時，相比于縱波時差，橫波時差受流體的影響更小，每單位孔隙度變化引起的橫波時差變化也比縱波時差變化大，橫波時差對孔隙度的反映更靈敏[7]，因此利用橫波計算孔隙度是可行的，且具有一定的優勢。

2004年Pride等[2]提出干巖石的剪切模量與骨架的剪切模量具有以下關系：

(1)

式(1)中：μd為干巖石的剪切模量，MPa；μma為骨架的剪切模量，MPa；φ為孔隙度，f；α為固結系數，無量綱，表示巖石孔隙結構的復雜程度，對于砂巖通常取2<α<20。等效介質理論指出固結系數α取決于巖石的孔隙結構和巖石骨架的剪切模量與體積模量之比。式(1)中常數1.5可以為2或者5/3，該因子選取的目的主要是為了在利用Pride巖石骨架模型反演橫波時差時，有較為精確的縱橫波速度比。為了避免式(1)中因子1.5選取的任意性，Lee[3]針對Pride模型的剪切模量公式做了進一步改進：

(2)

其中

(3)

Biot-Gassmann理論認為孔隙流體不改變飽和巖石的剪切模量，即巖石骨架的剪切模量等于飽和流體巖石的剪切模量[8-9]

μ=μd

(4)

式(4)中：μ為飽和流體巖石的剪切模量，MPa。

依據剪切模量與密度、橫波速度之間的關系，飽和流體巖石的剪切模量和骨架的剪切模量分別為

(5)

(6)

式(5)(6)中：ρ為飽和流體巖石的密度，kg/m3；Vs為飽和流體巖石的橫波速度，m/s；ρma為巖石骨架的密度，kg/m3；Vs,ma為巖石骨架的橫波速度，m/s。

因此,由式(2)～(6)可以得到

(7)

對于飽和流體泥質砂巖，其巖石體積物理模型為

ρ=(1-φ-Vsh)ρma+Vshρsh+φρf

(8)

式(8)中：Vsh為泥質含量，f；ρf為流體密度，kg/m3；ρsh為泥巖的密度，kg/m3。

橫波速度與橫波時差之間存在如下關系：

(9)

(10)

式(9)、(10)中：Δts為飽和流體巖石的橫波時差，s/m；Δts,ma為巖石骨架的橫波時差，s/m。

將式(8)～(10)代入式(7)整理后可得：

(11)

以Pride巖石骨架模型為基礎，結合Biot-Gassmann理論與巖石體積物理模型，式(11)最終建立了泥質砂巖儲層橫波時差與儲層孔隙度之間的關系。式(11)中的泥質含量Vsh可以通過測井曲線計算得到較為準確的數據，各種密度參數ρma、ρsh和ρf可根據油田實際選取。因此，如果得到巖石的骨架橫波時差Δts,ma和固結系數α就可以采用橫波時差利用式(11)計算儲層的孔隙度。所以，能否準確地求取固結系數和骨架橫波時差是利用該方法計算橫波孔隙度的關鍵。

2 參數確定方法

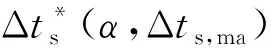
(12)

達到最小[10-11]，此時得到的骨架橫波時差Δts,ma和固結系數α即認為是巖石的骨架橫波時差和固結系數。

研究區渤中3油田東營組儲層為辮狀河三角洲沉積，砂體橫向展布穩定，砂體連片發育，單砂體厚度2.0～26.9 m，平均16.2 m，儲層巖性以中、細粒巖屑長石砂巖為主，礦物成分主要為石英、長石、巖屑，孔隙度范圍為16.4%～22.0%，平均為19.4%，為中孔隙度儲層。孔隙主要發育粒間孔，連通性較好，粒間充填礦物主要為伊利石、高嶺石。選取該油田取心探井BZ3-1井作為關鍵井，利用該井的伽馬曲線計算泥質含量，中子、密度曲線交會計算孔隙度，在此基礎上利用式(11)與式(12)進行骨架橫波時差和固結系數反演。圖1為關鍵井BZ3-1井利用孔隙度、泥質含量以及橫波時差反演的巖石骨架橫波時差和固結系數圖。圖中第6道和第7道分別為測井計算的泥質含量和中子、密度曲線交會計算的孔隙度與巖心分析數據的對比，可見二者計算的精度均較高，可以用于后續參數的反演；第9道為實測的橫波時差與反演的橫波時差之間的對比。在反演開始時，先分別給骨架橫波時差和固結系數賦初值，然后通過不斷地優化骨架橫波時差值和固結系數值，使得式(12)達到最小值，即實測的橫波時差與反演的橫波時差幾乎重疊，說明反演效果滿足要求，反演得到的骨架橫波時差和固結系數可以進行后續參數的擬合；第10道為最優化反演得到的骨架橫波時差，在儲層段(研究區泥質含量的有效厚度下限為0.2)骨架的橫波時差值在355 μs/m左右，在非儲層段隨著泥質含量的增加骨架的橫波時差值明顯增大；第11道為最優化計算的固結系數，固結系數隨著泥質含量的增加存在明顯增大的現象。

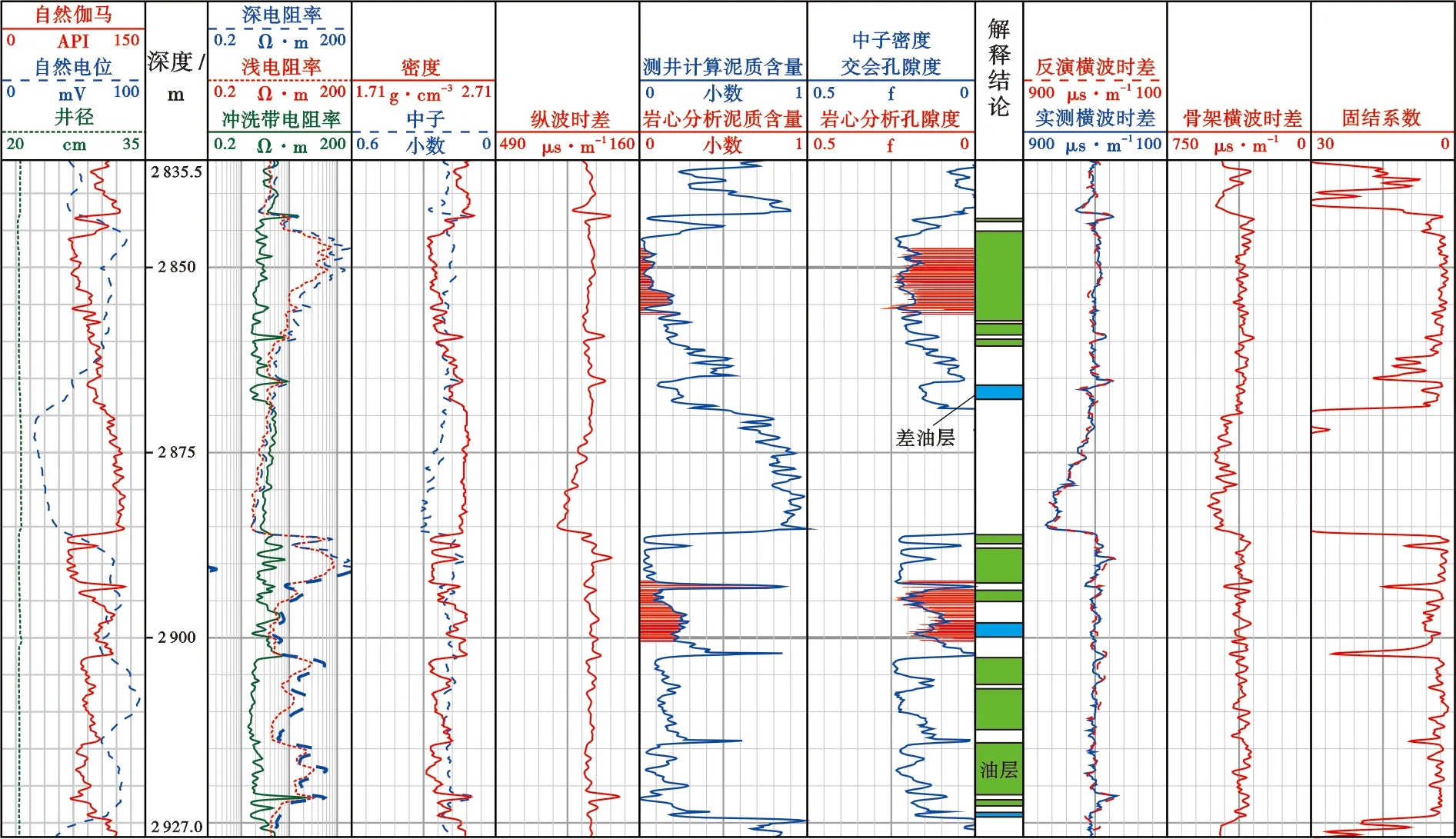
圖1 渤中3油田關鍵井BZ3-1井橫波孔隙度參數反演結果

在同一穩定分布的砂體中，黏土的礦物類型及分布形式是相對穩定的[12-13]。圖2為關鍵井BZ3-1與開發井BZ3-A井的黏土礦物掃描電鏡特征。該圖表明關鍵井與開發井儲層孔隙中充填的均為書頁狀高嶺石和絲片狀伊利石，黏土礦物的分布形式也較為一致。表1為關鍵井BZ3-1與開發井BZ3-A井東營組儲層的黏土礦物相對含量的對比。可見該油田關鍵井和開發井儲層中黏土礦物均以高嶺石為主，其次為伊利石和伊蒙混層，僅含少量綠泥石。因此，對于研究區來說，黏土的礦物類型和分布形式是較為穩定的，方法中涉及的骨架橫波時差和固結系數可以認為主要與泥質含量多少有關。

圖2 渤中3油田關鍵井BZ3-1井與開發井BZ3-A井黏土礦物掃描電鏡特征

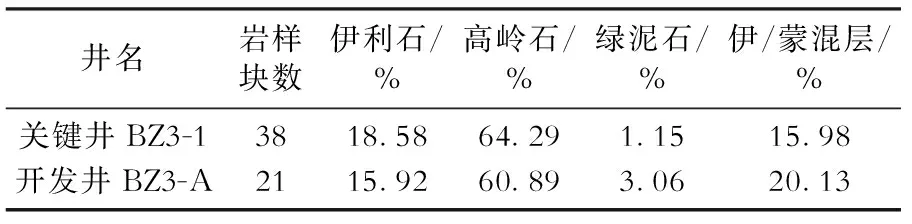
表1 渤中3油田關鍵井BZ3-1井與開發井BZ3-A井黏土礦物相對含量對比

在關鍵井BZ3-1井中選取穩定發育的砂巖段和泥巖段，分別利用泥質含量建立骨架橫波時差和固結系數的計算公式，并將其應用到采用聲波測井的開發井中，從而能夠利用式(11)計算橫波孔隙度。圖3為巖石的骨架橫波時差與泥質含量的關系，圖4為固結系數與泥質含量的相關性。由兩圖可見，二者與泥質含量均具有較好的相關性。擬合得到的公式分別如下：

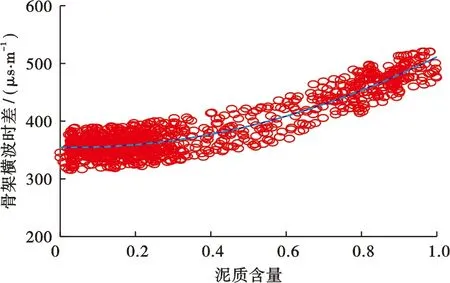
圖3 渤中3油田關鍵井BZ3-1井骨架橫波時差與泥質含量關系

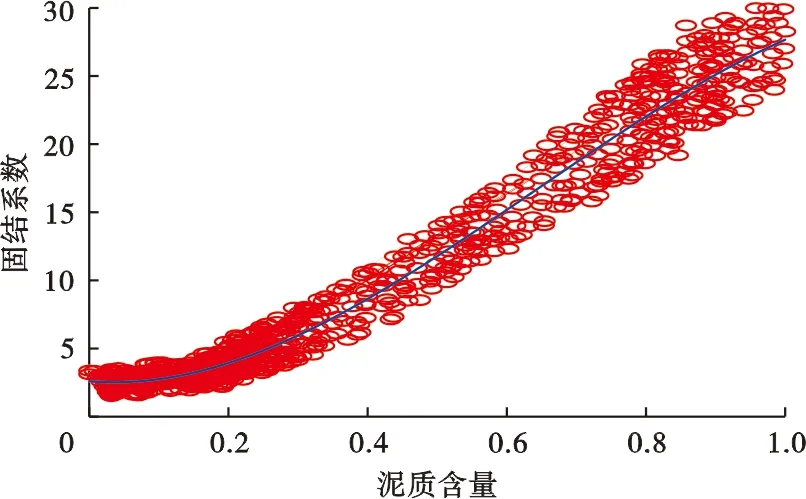
圖4 渤中3油田關鍵井BZ3-1井固結系數與泥質含量關系

骨架橫波時差

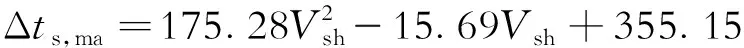
(13)

固結系數

(14)

3 應用效果分析

渤中3油田開發井BZ3-A井在實施過程中孔隙度測井采用過套管聲波測井，未進行中子和密度測井。將利用BZ3-1井建立的骨架橫波時差和固結系數的計算公式應用于該井中，采用Pride巖石骨架模型計算橫波孔隙度。圖5為該井測井曲線及橫波孔隙度處理結果。第11道為采用Pride巖石骨架模型計算的橫波孔隙度和采用威里平均時間公式計算的縱波孔隙度與巖心分析孔隙度的對比。

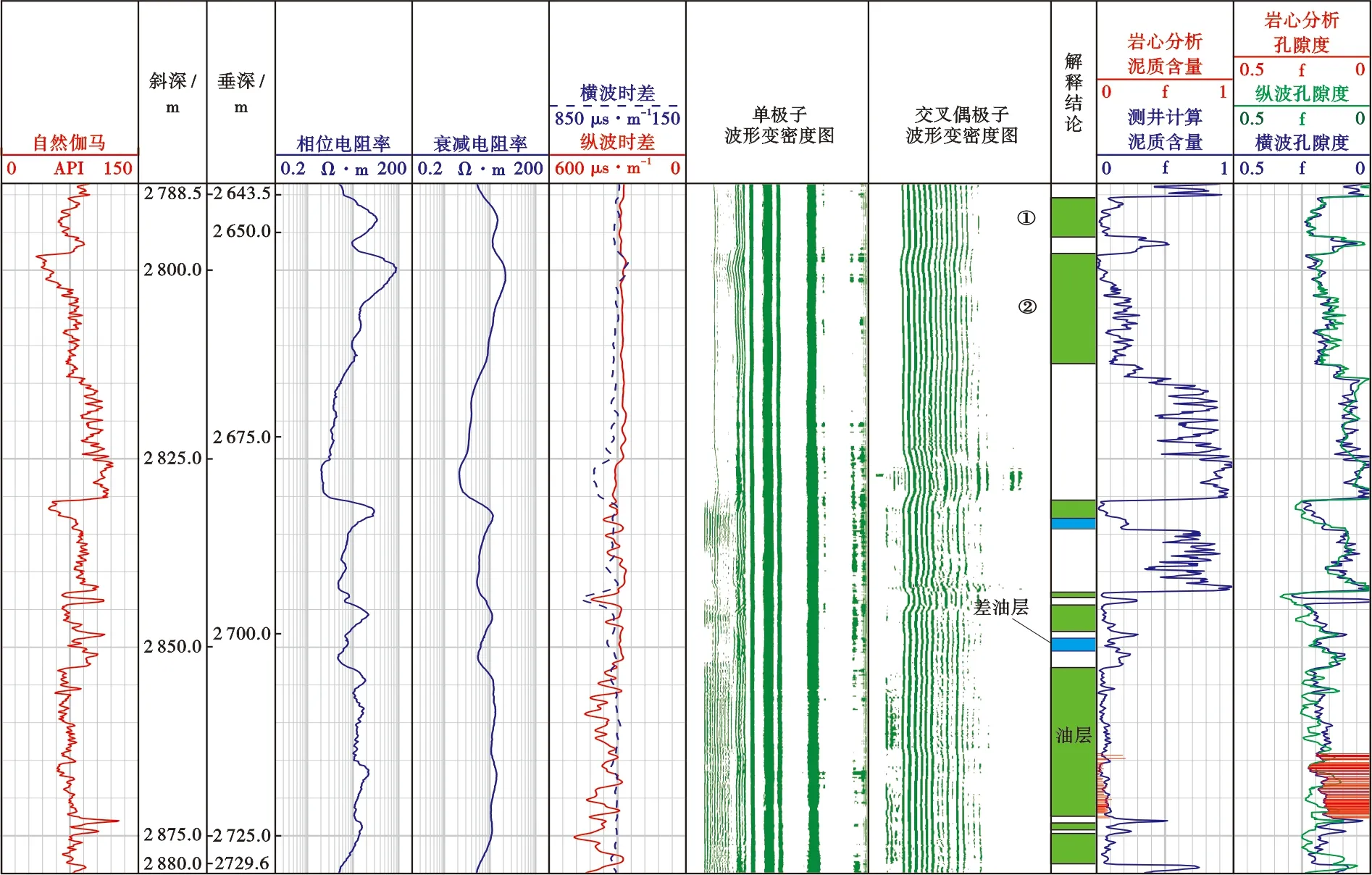
圖5 渤中3油田開發井BZ3-A井橫波孔隙度處理結果

BZ3-A井在斜深2 788～2 830 m井段固井質量較好，過套管聲波測井獲得的單極子波形(第7道)和偶極子波形(第8道)質量均較高，從而能夠提取可靠的縱、橫波數據。由圖5可知，在斜深2 788～2 830 m井段橫波孔隙度與縱波孔隙度對應較好，圖中油層①測井計算的橫波孔隙度為20.1%，縱波孔隙度為20.3%，油層②測井計算的橫波孔隙度為17.8%，縱波孔隙度為16.9%,兩層分別采用兩種方法計算的孔隙度均比較接近，都能夠較為真實地反映儲層物性。在斜深2 830～2 880 m井段固井質量較差，由于交叉偶極聲源工作頻率為低頻，低頻聲源產生的能量穿透性較強，而單極子聲源工作頻率較高，相對來說穿透性較差，受附近井眼狀況影響較大；同時橫波測量的是撓曲波(非對稱波)，當固井質量不好時，套管與地層之間通常為非均勻環境，相比于單極子接收器，偶極子接收器對于非對稱波更敏感，對接收撓曲波信號相對有利。因此，在2 830～2 880 m井段單極子波形中由于包含套管波信息(第5道左側變密度顯示區域)，使得提取的縱波時差受到套管波的影響，出現明顯的異常現象，而偶極子波形質量較高，從而能夠準確地提取地層的橫波。從第11道該井段兩種孔隙度與巖心分析孔隙度對比可知，橫波孔隙度與巖心分析孔隙度較為吻合，縱波孔隙度則由于波形質量的問題與巖心分析孔隙度差別較大。表2為取心井段(2 864～2 873 m)橫波孔隙度和縱波孔隙度與巖心分析孔隙度的對比，從表中可以看出，在取心井段，采用橫波計算的孔隙度與巖心分析孔隙度較為接近，而縱波孔隙度則與巖心分析孔隙度差別較大。采用本文方法計算的橫波孔隙度精度更高，為孔隙度計算提供了一種有效的方法。

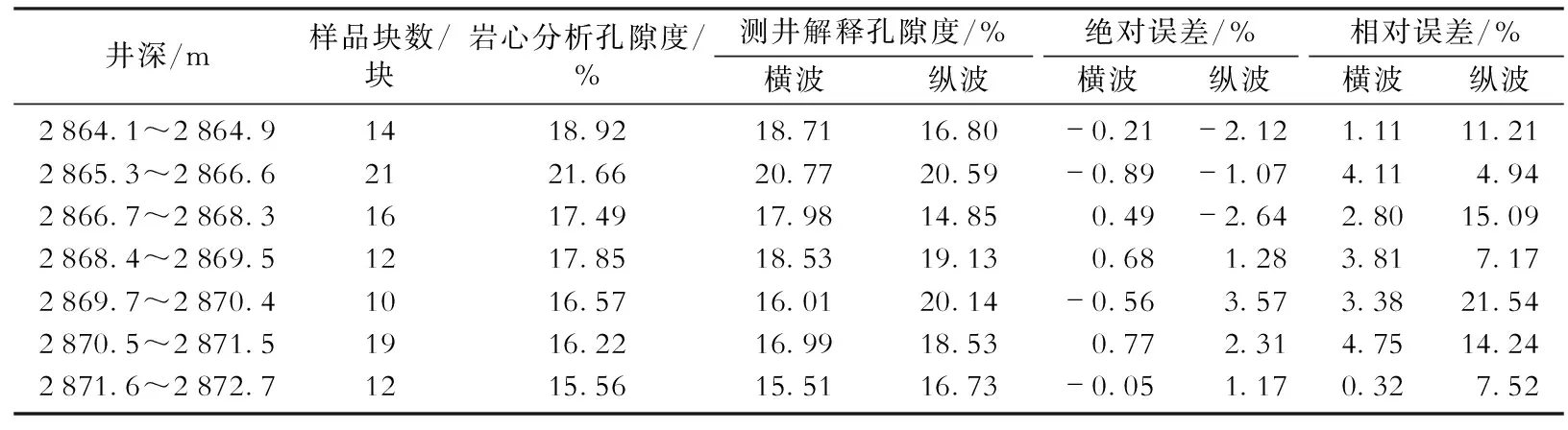
表2 渤中3油田開發井BZ3-A井橫波孔隙度、縱波孔隙度與巖心分析孔隙度對比表

4 結論

1) Pride巖石骨架模型建立了巖石骨架與巖石基質之間的關系，且適用于中低孔隙度儲層。通過該模型結合Biot-Gassmann理論以及巖石體積物理模型，建立了泥質砂巖儲層橫波時差與儲層孔隙度之間的關系，通過該關系進而可以利用橫波時差計算儲層孔隙度。

2) 對于Pride巖石骨架模型中涉及的骨架橫波時差和固結系數2個參數，提出了最優化的反演方法，并利用測井參數擬合得到2個參數的計算公式，為方法的進一步推廣應用奠定了基礎。

3) 在同一穩定展布的砂體中泥質的礦物類型及分布形式相對穩定的假設下，將建立的基于Pride巖石骨架模型的橫波孔隙度計算方法應用于研究區開發井中，取得了較好的實際應用效果。