CNS/SINS陀螺標定系統在UUV中的應用
劉志浩,于雪泳,許忠良
(海軍潛艇學院,山東 青島 266000)
0 引 言
UUV作為一種新型海上軍事裝備與海上科研裝備,憑借其出色的隱蔽性、環境適應性,能夠在水下載人平臺難以抵達的區域執行的多種任務,在軍民領域均獲得了廣泛關注。在軍事應用中,UUV的突出特點是具有極強的隱蔽性與及安全性,且造價低廉。它的體積遠小于潛艇等有人平臺,使得敵方的反潛兵力難以發現及破壞,無人駕駛的特征使其可以前往危險海域執行任務,低廉的造價使UUV可以大量部署,在水下戰場中以數量上的優勢取得主動權,形成非對稱優勢。
從隱蔽性角度考慮,理想過程是UUV能夠始終潛在水下,然而由于導航原理與技術限制,電磁信號無法透入水下,當前成熟的基于電磁信號的組合導航技術在水下無法使用。常見的幾種水下輔助導航系統也存在一定的缺陷與弊端。多普勒導航系統在深海區域受水深限制無法使用,在軍事行動中在淺海區域使用也容易因聲波而暴露位置;水聲定位導航系統需要其他兵力或設備進行保障,在民用領域中這些保障設備對資金的需求較大,在軍用領域中這些水上或水下的保障設備目標較大且機動性不高,基于聲波的方式也仍未解決隱蔽性問題,限制條件較多。
考慮到UUV與控制平臺的必要交互(如自身狀態或無法處理的問題等),UUV需要定期上浮通信。通常采用的方式是在上浮通信過程中以SINS/GPS組合導航的方式校準系統誤差。然而衛星導航系統的輸出頻率通常不高,且受海面環境影響衛星信號的持續穩定跟蹤存在一定難度,校準過程消耗時間較長,部分情況下甚至可達數十分鐘,長時間的水面狀態將對隱蔽性造成極大破壞[1]。若僅采用GPS提供的位置和速度進行重置,由于無法確定姿態失準角及陀螺漂移量,在后續航行中導航誤差將繼續發散。
基于星敏感器的天文導航系統(CNS)輸出的是高精度姿態信息,在位置和時間已知情況下,任意恒星相對當前位置的赤經和赤緯均可確定[2]。在UUV的校準過程中,可由星敏感器確定載體姿態,同時由GPS確定載體位置和速度,并通過合適的觀測方式確定出陀螺的漂移,降低校準時間且提高估計精度。
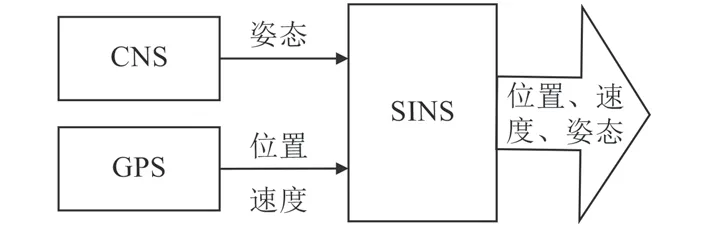
圖1 CNS/GPS/SINS組合系統框圖Fig. 1 Integratedsystemof CNS/GPS/SINS
1 誤差分析及測量原理
1.1 陀螺儀誤差模型
陀螺儀的系統性誤差主要包括4部分:常值項、隨溫度變化項、逐次啟動項和工作期間變化項。常值項為每次開機均會存在的常數型誤差,可由內場標定結果進行補償;溫變項也可根據內場標定結果,結合傳感器當前工作溫度進行相應補償;逐次啟動項在每次開機過程中均發生變化,但在當次工作階段內保持不變,主要通過對準或組合導航過程對其進行標校;工作期間變化項是在每次開機后都會隨時間發生緩慢變化的誤差項,理論上可以通過構建復雜的模型進行修正,但實際上實現難度極大[3]。
考慮到真正決定慣性導航系統精度和組合模型設計的是經過修正常值項后的誤差,因此文章假定常值誤差項及溫變項已獲得補償,只考慮逐次啟動項和工作期間變化項。這2項誤差可等效為隨機常數誤差和隨機誤差,隨機常數誤差主要體現為常值漂移和標度因子誤差,當考慮標度因子誤差與其他軸向不相關時,可以等效為常值漂移的附加項,因此陀螺的誤差模型可表示為[4]:

式中:ε為陀螺誤差;ξ為隨機常數誤差;nr為白噪聲。
1.2 CNS姿態測量
姿態的表示方式通常有歐拉角法、余弦矩陣法和四元數法,三者理論上是等價的,但根據模型的不同,在3種方法在計算復雜度及精度上存在差異。姿態余弦矩陣法易于理解,但由于呈非線性,且在部分180°附近容易出現奇點,在高階展開過程中也容易丟失精度,而四元數方法能夠有效避免這些問題,因此文章中主要采用四元數進行計算,此時載體姿態可以表示為[5-7]:
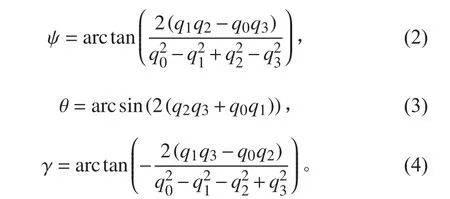
式中:ψ為航向角;θ為俯仰角;γ為橫滾角;qi(i=1,2,3,4)為四元數中第i個量。
CNS是以星敏感器為核心的導航定位系統。星光信號經光敏元件光電轉換后,可結合導航星庫確定載體姿態,具有精度高、質量小、功耗低、無漂移和工作方式多樣等特點,同樣具有無源自主導航能力,是一種性能優良、發展前途廣闊的姿態測量部件[2]。
在慣性空間內,可認為由地心指向恒星的矢量是穩定的。此時,載體測得的星矢量僅與載體坐標(b系)相對慣性坐標系(i系)的姿態有關,考慮到導航坐標系(n系)通常選取為地理坐標系(t系),因此也可認為星矢量與地球坐標系(e系)、n系和i系的相對關系有關。假設星敏感器的測量坐標系(s系)與b系一致,由星敏感器測得的星矢量可表示為[xb,yb,zb]T,令Ub,j表示測得的第j顆星矢量在b系中的投影的列向量,令Ui,j表示該星矢量在慣性空間中的投影的列向量,則載體的在慣性空間內的姿態余弦矩陣最小二乘表示為:
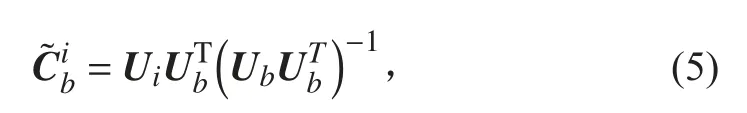

2 卡爾曼濾波器構建
2.1 狀態方程構建
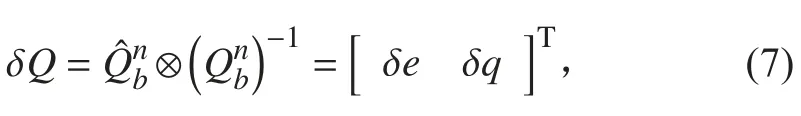
其中:δe為 標量部分;δq為矢量部分。
假設四元數已正規化,則逆與共軛相等:

將式(8)代入式(7)后求導可得:
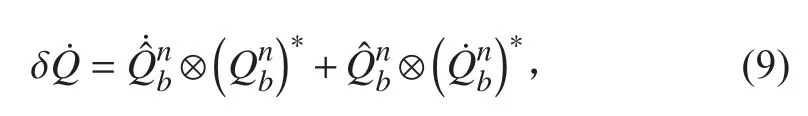
約定三維矢量與四元數乘時,將三維矢量擴展為四元數的矢量部分,標量部分為0,根據四元數微分方程有[10]:
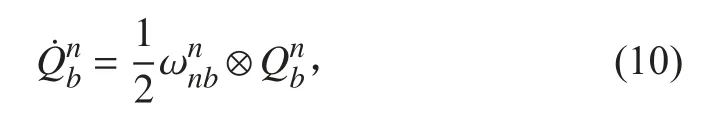
將式(10)代入式(9)可得:
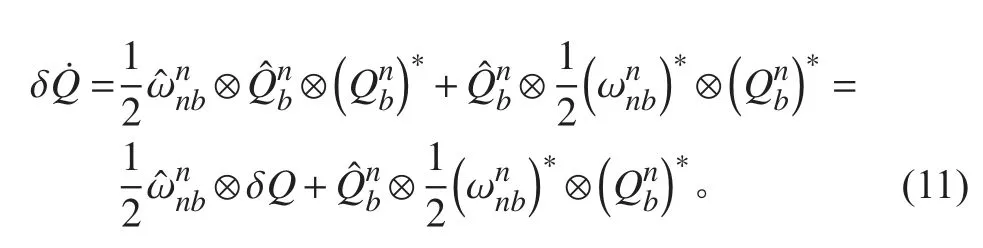
根據四元數乘法規則,令
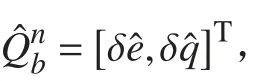
則有:
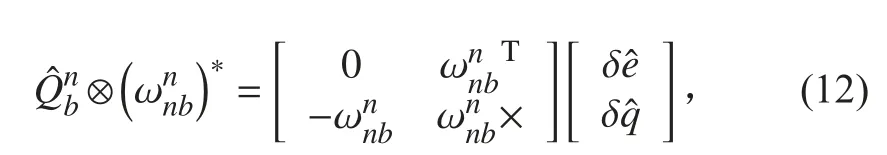
將式(12)代入式(11)右邊第2部分可得:

將式(13)代入式(11)可表示為:

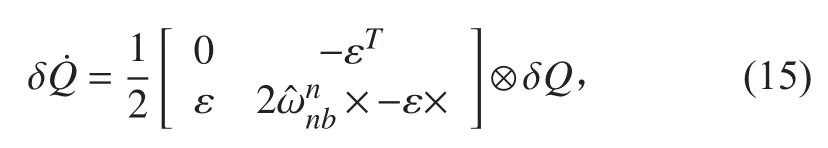
考慮δQ表示由n系轉向計算導航坐標系(n′系)的小角度四元數。根據等效旋轉矢量原理,繞定軸轉動θ時,四元數的標量部分為cosθ/2,因此在δQ中可認為標量部分δe=1,忽略二階小量叉乘,四元數的矢量部分為:
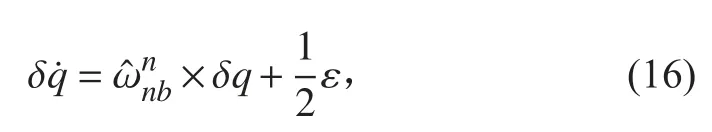
根據式(1),取狀態向量為:

則狀態方程為:
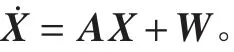
其中:
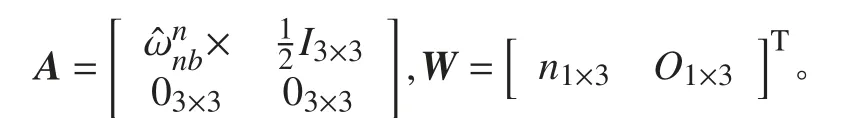
2.2 量測方程構建
由于CNS測得的是載體的高精度姿態輸出,令其轉換為四元數后表示為QCNS,SINS推算得到的姿態轉換為四元數后表示為QSINS,根據式(7)運算后取矢量部分作為觀測值,則量測方程為:
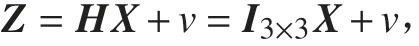
式中I3×3表示三維單位矩陣。
連續時間系統不符合計算機采樣計算過程,需要進行狀態方程的離散化。離散化后系統可表示為:
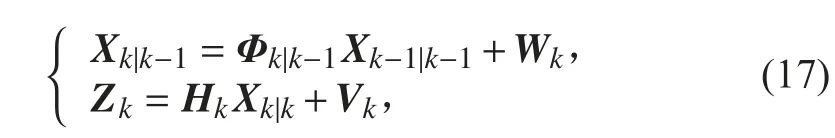
時序上的濾波過程為:

3 仿真驗證
為驗證算法有效性,采用Matlab進行仿真分析,模擬UUV海上上浮校準過程中,采用CNS進行脫落常值標定。
3.1 仿真參數設置
假設UUV的上浮點坐標為135.00°E,25.00°N,測星時刻為2018.12.01日05時30分00秒,慣性坐標系取2018.12.01日00時00分00秒的地球坐標系,GPS的定位誤差為20 m,UUV陀螺儀的常值漂移分別為0.05°/h,0.1°/h和0.2°/h,CNS測量精度為5'',SINS采樣間隔0.02 s,CNS輸出頻率為2 Hz。3顆選定的單位星矢量在慣性坐標系內的坐標表示為:

3.2 仿真分析
根據上述仿真設定,利用Matlab進行仿真驗證,對陀螺儀常數漂移的仿真結果如圖2~圖4所示。
仿真結果表明,該模型可以在20 s左右進入穩定狀態,在50 s左右即可獲得較為準確的陀螺常值漂移估計值,精度可達95%以上。
4 結 語
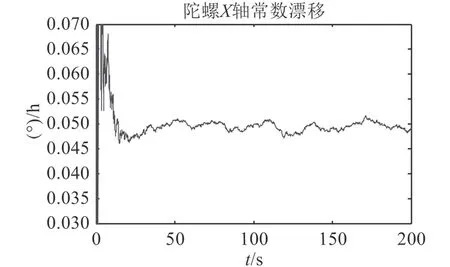
圖2 X軸方向陀螺常值漂移估計Fig. 2 Random constant drift in axis X

圖3 Y軸方向陀螺常值漂移估計Fig. 3 Random constant drift in axis Y
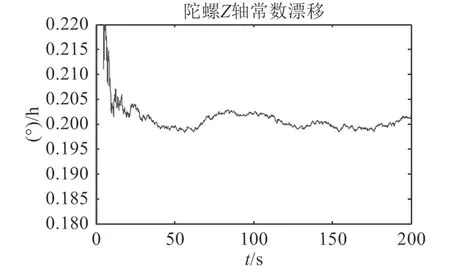
圖4 Z軸方向陀螺常值漂移估計Fig. 4 Random constant drift in axis Z
CNS能夠提供不隨時間發散的穩定的高精度姿態信息,而GPS能夠提供不隨時間發散的穩定的位置和速度信息,二者組合在一起時具有極強的互補性。GPS/SINS系統進行失準角和陀螺漂移校準時,需要較大機動以增強可觀性,而這與UUV上浮后需要停車,避免螺旋槳擊打海面造成損壞這一工程實現的實際情況不相吻合,引入CNS后能夠有效解決這種問題。利用Matlab對標定系統進行仿真,驗證了其在標定陀螺常值漂移方面的可行性。以這種方法進行標定后,可結合CNS給出的精確姿態,降低GPS/SINS組合導航中狀態變量的維數,縮短上浮校準時間,為增強UUV的隱蔽性與安全性提供一種解決問題的思路。

