基于多匝光纖環的盤式光纖加速度計理論模型

馬坤，于天明，楊繼勇，年華，李愛秋，楊木森

1.黑龍江省地震局賓縣地震臺，黑龍江哈爾濱150400

2.哈爾濱工程大學物理與光電工程學院，黑龍江哈爾濱150001

振動傳感器種類繁多，加速度計在振動傳感器中占有重要的地位并且應用領域廣泛[1]，例如：建筑監測、車輛控制、地震預報、油田勘探、航空制導等[2]。傳統的加速度計多為機電式加速度計[3]，受限于電子元件的工作特點，機電式加速度計不適合在強電磁干擾或高溫的環境中使用。光纖加速度計作為一種新型加速度計，具有靈敏度高、抗電磁干擾、能在較高溫度下工作以及易于大規模組網等優點[4-5]，相比傳統的機電式加速度計具有更廣闊的發展前景。在各種光纖加速度計中，盤式光纖加速度計具有動態范圍大、靈敏度高、工作頻帶寬的優點[6-7]，得到了廣泛研究與應用。

盤式光纖加速度計的工作原理是彈性盤受外界振動作用而產生應變，固定在彈性盤表面的傳感光纖也會產生應變，采用光學相干原理將光纖應變轉換為光學相位變化即可檢測外界加速度[8-9]。從1990年被發明出來至今，盤式光纖加速度計吸引了眾多研究者的目光，例如通過使用微光纖并且優化光纖環的位置來提升盤式光纖加速度計的性能[10]。盤式光纖加速度計的工作特性比較復雜，包括靈敏度和諧振頻率在內的性能參數受到許多因素的共同作用，因此在實用化的過程中必須建立準確的理論模型來指導盤式光纖加速度計的設計與優化。

前人發表過一些基于單匝光纖環的盤式光纖加速度計理論模型，這些理論模型沒有體現單匝光纖環對彈性盤的機械性能的影響。自從Geoffrey A.Cranch 等[11]通過多匝光纖環來提高盤式光纖加速度計的靈敏度以來，采用多匝光纖環成為研制盤式光纖加速度計的趨勢。然而，光纖環匝數的大幅增加使其對彈性盤的機械性能的影響愈加顯著，因而基于單匝光纖環的理論模型不能準確計算出基于多匝光纖環的盤式光纖加速度計的性能參數。

本文采用彈性力學和材料力學的相關理論，建立了基于多匝光纖環的盤式光纖加速度計的理論模型，對靈敏度和諧振頻率進行了理論推導；采用有限元仿真軟件建立了基于多匝光纖環的盤式光纖加速度計的仿真模型，分析了理論模型和仿真模型之間的誤差來源；對研制出的盤式光纖加速度計進行了性能測試，并將測試結果與仿真結果進行了對比。

1 系統結構及理論分析

盤式光纖加速度計是一種彈簧-質量體系，可以將外界的加速度轉化為光纖長度變化，進而使光纖干涉儀輸出光信號相位差發生改變。

圖1是盤式光纖加速度計的工作原理圖。基于多匝光纖環的盤式光纖加速度計的拾振結構由彈性盤、質量塊、多匝光纖環、封裝結構組成。當封裝結構受到外界軸向加速度作用時，質量塊由于慣性會向彈性盤施加軸向力，使彈性盤發生彎曲并使其上下表面產生等幅反向的應變分布；將作為光纖Michelson 干涉儀兩傳感臂的2個多匝光纖環分別粘貼于彈性盤上下表面，當彈性盤發生應變時，其上下表面的光纖環受到應變傳遞作用而分別發生拉伸或壓縮，進而干涉儀兩臂光信號的相位差變化，導致輸出干涉信號強度的改變，最后通過對干涉信號進行探測并解調相位變化信息，實現對外界加速度的測量。由于彈性盤半徑遠大于厚度，因此對軸向加速度具有很高的響應度。

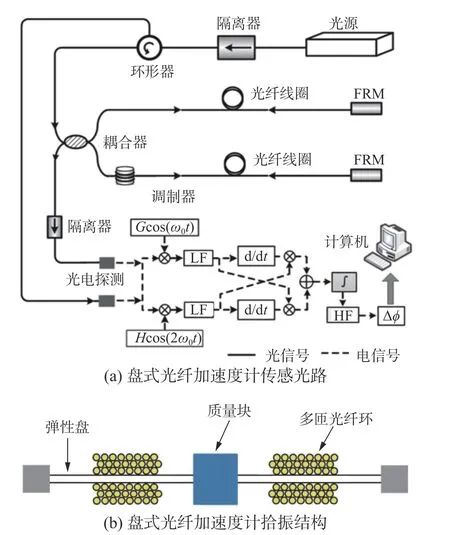
圖1 盤式光纖加速度計傳感系統

靈敏度用來衡量加速度計對外界加速度的響應程度，諧振頻率決定了加速度計的工作帶寬。下面探究基于多匝光纖環的盤式光纖加速度計的靈敏度和諧振頻率的理論模型。

多匝光纖環對彈性盤的機械參數的影響不能忽略，例如楊氏模量、泊松比和厚度都發生了變化。下面采用混合材料力學的體積平均法來計算等效機械參數。設彈性盤的外半徑為a、內半徑為b、厚度為t，在上下表面粘接光纖環后的彈性盤的等效機械參數為

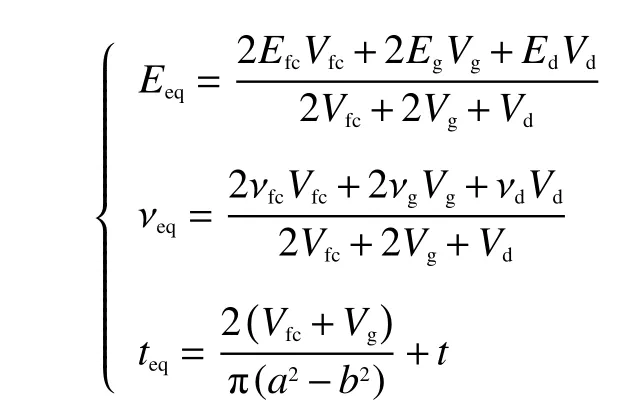
式中：E為楊氏模量；v為泊松比；V為體積。其中下標fc、g、d 分別表示光纖環、將光纖環粘接在彈性盤上的環氧樹脂膠、彈性盤。

粘接有光纖環的彈性盤的等效彎曲剛度系數可以表示為

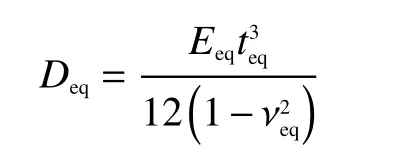
彈性盤外邊緣受到封裝結構的固定支撐，內邊緣被質量塊夾緊，發生彎曲的彈性盤的徑向轉角為[12]

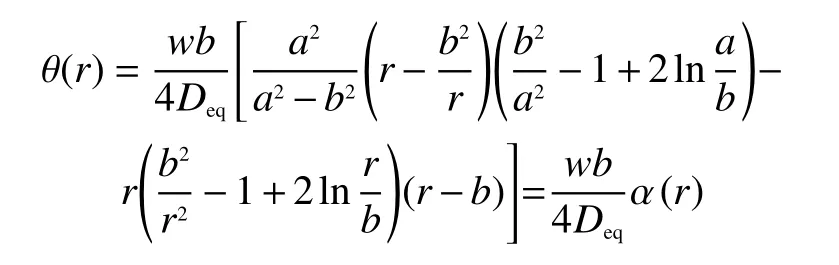
式中：r為彈性盤半徑；w是線載荷。設拾振結構所受外界加速度為A，質量塊質量為M，w可以表示為

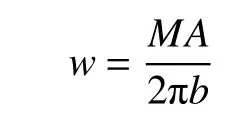
在彈性盤半徑為r、軸向高度為z處的環向應變的表達式為

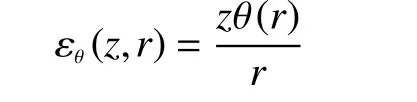
在光纖環高度為z的這一匝光纖的長度變化可以通過對這一匝光纖的環向應變積分得到，表示為

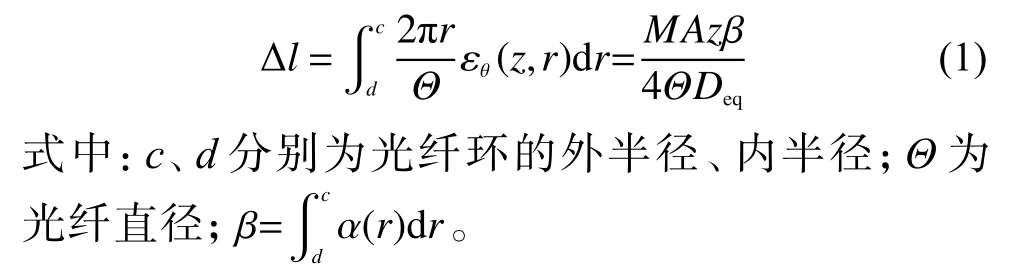
設t1為光纖環與彈性盤之間的粘膠厚度。在匝數為n的多匝光纖環中，第1匝和第n匝光纖的高度分別為

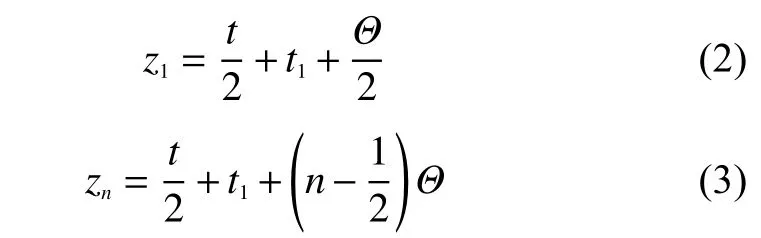
將式(2)、(3)分別代入式(1)中得到第1匝和第n匝光纖的長度變化Δl1和Δln。由式(1)可以看出應變引起的某一匝光纖的長度變化和其所處的高度z成正比，因此，多匝光纖環的光纖長度變化可以表示為

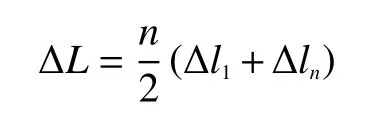
光纖中的相位變化可由光纖長度變化得到：

式中

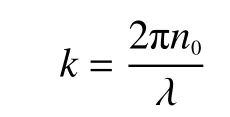
其中：n0為光纖纖芯折射率；λ為干涉儀光源的波長。

由于光纖Michelson 干涉儀的2個傳感臂上各有一個光纖環，并且每個光纖環中光信號都經過2次，干涉儀輸出的相位差的變化為式(4)的4倍，選擇靈敏度的單位為rad/g，加速度計的靈敏度表達式為

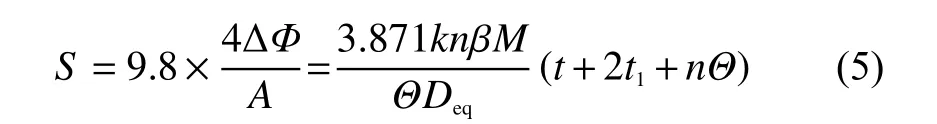
盤式光纖加速度計的拾振結構可以等效為受迫振動的彈簧-質量系統，彈簧的剛度由彈性盤和2個多匝光纖環在軸向的剛度共同組成，質量來自質量塊。

彈性盤最大撓度在其內半徑處，可以表示為

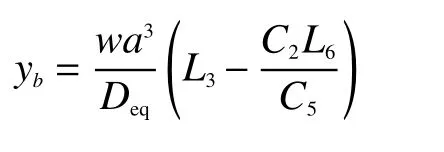
式中：

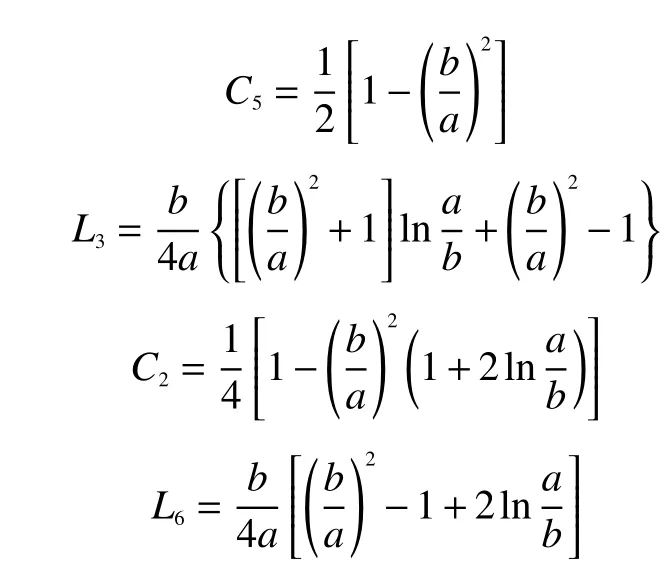
根據廣義胡克定律得到粘接多匝光纖環的彈性盤的等效剛度系數為

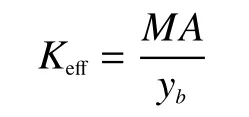
基于多匝光纖環的盤式光纖加速度計的諧振頻率為

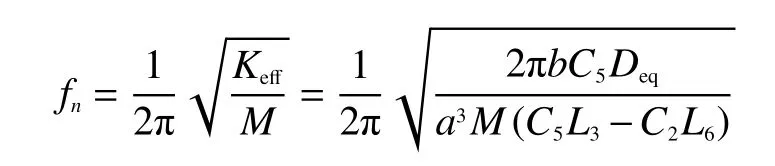
采用表1的參數對基于多匝光纖環的盤式光纖加速度計的性能參數進行理論計算，得到靈敏度為4 102 rad/g，諧振頻率為302.4 Hz。

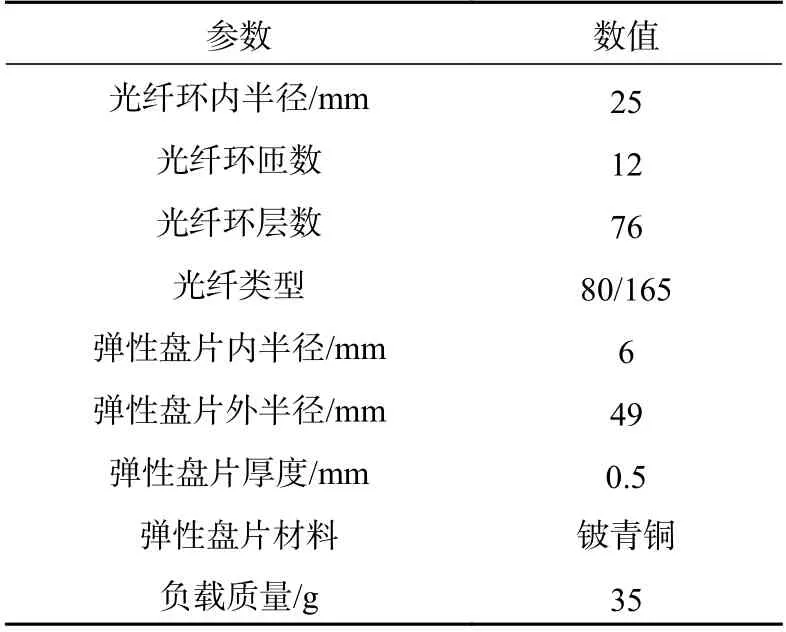
表1 盤式光纖加速度計制作參數

2 有限元仿真

采用有限元仿真軟件建立基于多匝光纖環的盤式光纖加速度計拾振結構的仿真模型。

采用的有限元仿真軟件可以對加速度計的拾振結構進行比較精準的幾何建模和材料參數設置，并對模型施加非常接近實際情況的固體力學條件。采用表1的參數建立仿真模型，進而可以通過軟件計算得到光纖環的應變分布和拾振結構的諧振頻率，由光纖環的應變分布可以很方便地計算出加速度計的靈敏度。

采用二維軸對稱方法建立拾振結構的幾何模型，如圖2所示。即在經過對稱軸的截面上建立二維幾何模型，仿真軟件會將該二維幾何模型繞對稱軸旋轉360°，形成三維幾何模型。

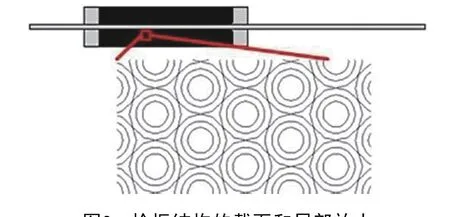
圖2 拾振結構的截面和局部放大

對模型施加沿對稱軸方向的g=9.8 m/s2的重力場，采用穩態研究得到截面上的環向應變分布，如圖3所示。

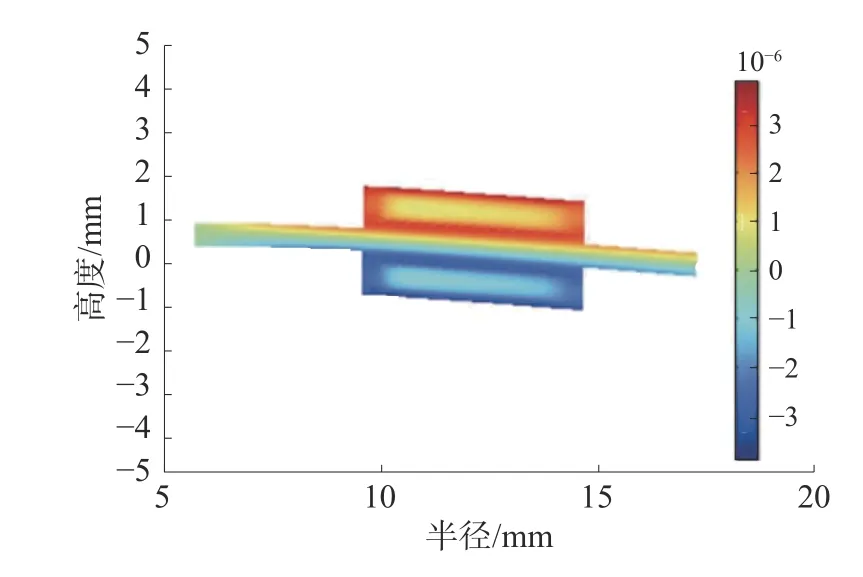
圖3 環向應變分布

通過二維截點可以獲得每一圈光纖纖芯的環向應變和周長改變量，求和得到一個光纖環的長度改變ΔL，代入式(5)即可得到仿真靈敏度，其值為2 563.25 rad/g。

采用特征頻率研究即可得到拾振結構的仿真各階諧振頻率，其中一階諧振頻率最小，為250.38 Hz。

可以看出，由理論模型和仿真模型得到的靈敏度是相差較多的，下面對產生這種誤差的原因進行分析。

圖4是沒有粘接光纖環的彈性盤片表面的環向應變分布，可以看出理論計算結果和仿真結果吻合較好。

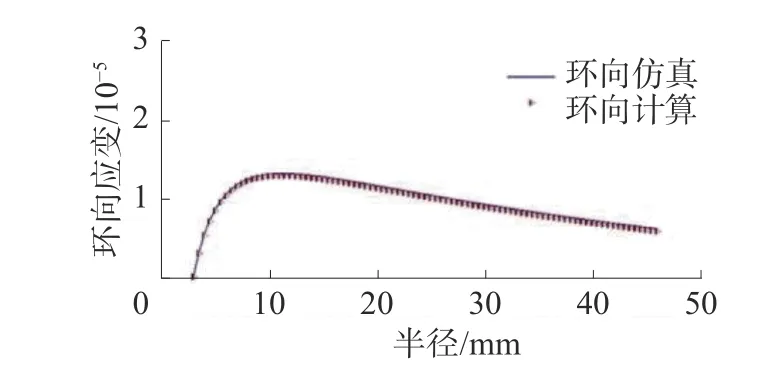
圖4 彈性盤表面環向應變分布

在理論模型中將粘接光纖環的彈性盤等效為一個均勻介質的圓盤，然而實際上光纖環只覆蓋了一部分彈性盤。圖5是光纖環粘接在彈性盤內側時環向應變的理論計算結果和仿真結果，從仿真結果可以看出，彈性盤內側的環向應變相比趨勢線明顯較小，這是因為在粘接光纖環的位置，彈性盤具有較大的剛度，而理論模型不能體現這一特點。因而對于光纖環的環向應變，仿真結果小于理論計算結果，產生仿真和理論計算之間的誤差。

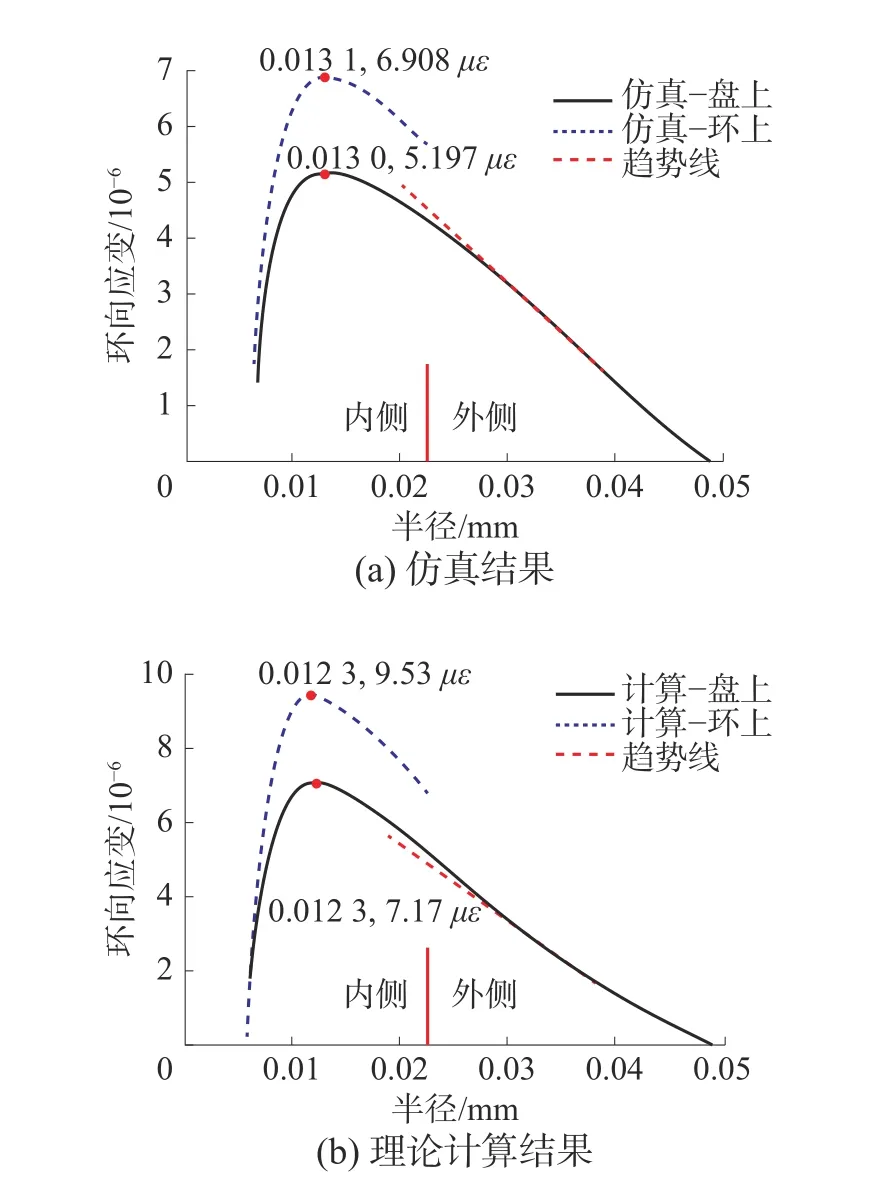
圖5 環向應變分布對比

光纖環和彈性盤屬于不同材質，二者還需用膠來粘接，應變無法完全從一種材料傳遞到另一種材料，存在應變傳遞率。應變傳遞率與材料的力學參數和幾何參數都有關，無法將應變傳遞率進行定量計算，這會導致理論計算結果和仿真結果之間的偏差。

3 實驗測試

按照表1的參數實際制作了盤式光纖加速度計，并對其進行測試，測試系統如圖6所示。參考加速度計為石英加速度計，振動臺產生的振動信號同時施加到盤式光纖加速度計和參考加速度計上，計算機可以同時得到2個加速度計的輸出信號，參考加速度計從而可以對盤式光纖加速度計進行標定。

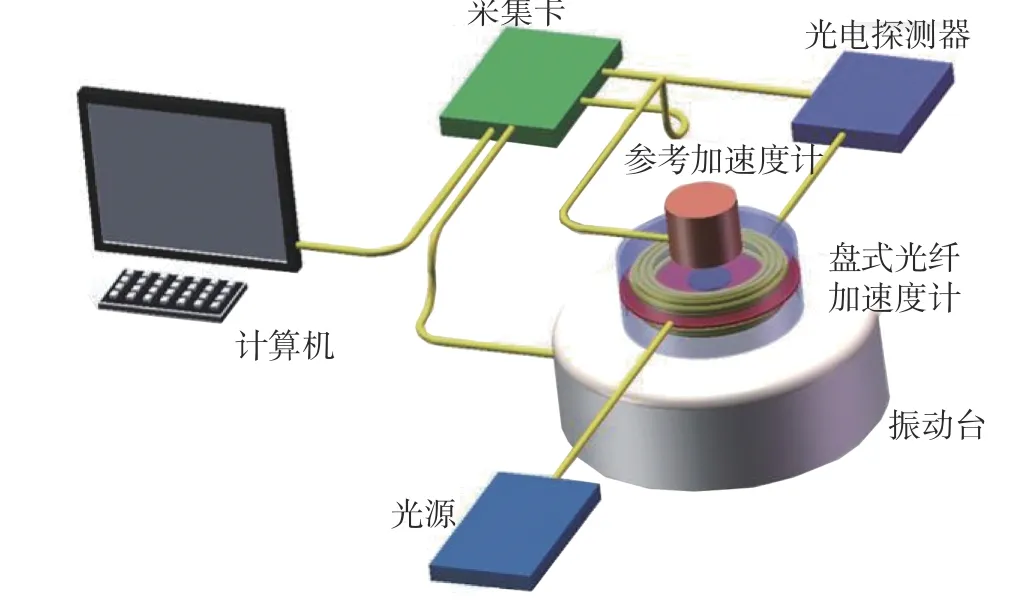
圖6 光纖加速度計測試系統

進行諧振頻率測試時保持參考加速度計測得的加速度幅值恒定，調節振動臺的振動頻率，得到盤式光纖加速度計的幅頻特性曲線，如圖7所示。實際制作的盤式光纖加速度計的諧振頻率在212 Hz 附近，仿真得到的諧振頻率與實驗結果相差18.1%；在150 Hz 以內盤式光纖加速度計的響應穩定，因此該盤式光纖加速度計的工作帶寬為150 Hz。

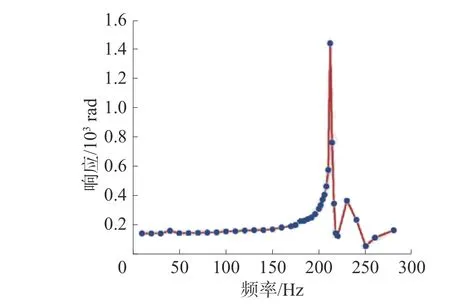
圖7 盤式光纖加速度計幅頻特性曲線

測試靈敏度時使振動臺產生40 Hz 的振動信號，改變振動信號的幅度并對盤式光纖加速度計的輸出信號進行測量，得到盤式光纖加速度計的加速度響應曲線，如圖8所示。可以看出研制的盤式光纖加速度計對外界加速度的響應是非常線性的。曲線的斜率為盤式光纖加速度計的靈敏度，為2 834.29 rad/g，仿真得到的靈敏度與其相差-9.6%。

圖8 盤式光纖加速度計加速度響應曲線

4 結論

本文建立了基于多匝光纖環的盤式光纖加速度計的理論模型與有限元仿真模型，并對研制的盤式光纖加速度計進行了實驗測試，得到如下結論：

1)理論模型給出了靈敏度和諧振頻率的表達式，但在準確度上還有提升空間；

2)實驗測得的靈敏度為2 834.29 rad/g，諧振頻率為212 Hz，仿真模型得到的靈敏度和諧振頻率分別和實驗結果相差-9.6%和18.1%；

3)本文建立的理論模型和仿真模型對基于多匝光纖環的盤式光纖加速度計的研制具有重要的指導作用。