基于運動過程還原法的液壓支架巡檢機器人位姿檢測
楊學軍,王然風,王懷法,李衛國
(太原理工大學 a.礦業工程學院,b.工程訓練中心,太原 030024)
在煤礦開采少人化和無人化[1-2]進程中,液壓支架位姿和直線度的正確性是保證工作面能夠自動連續推進的關鍵[3-4]。只有保證液壓支架排成直線,才能把與之互為支點進行推拉前進的刮板輸送機推直,然后才能保證以刮板輸送機為運行軌道的采煤機走直線,從而把煤壁切直[5]。單個支架位姿不僅反映了整個支架群直線度,還部分反映了工作面地板地質情況和頂部來壓情況。因此,國內外許多學者積極研究工作面的直線度檢測和控制問題[6],有些學者以刮板輸送機為主要研究對象[7-9],有些學者以液壓支架為主要研究對象[10]。
澳大利亞的LASC技術[11-12]是通過在采煤機上安裝三維陀螺儀和慣性導航儀,得到采煤機機身的運動速度、姿態和位置信息,利用行走軌跡判定刮板輸送機的軌道直線度,進而通過液壓支架調整刮板輸送機的位置,實現直線度控制。基于視覺的刮板機直線度測量方法[13-14]通過控制刮板輸送機溜槽上安裝的LED燈點亮和熄滅,利用攝像儀測量計算每節溜槽偏移度。基于超聲波傳感器測量千斤頂位移量的刮板輸送機調直方法[15]采用超聲波傳感器測量千斤頂位移量并傳輸至控制臺,經數據比對后,自動調整刮板輸送機的直線度。
基于激光對位傳感器測量液壓支架相對位移的直線度控制方法[16-17]是在每臺液壓支架上各安裝一個激光對位傳感器,根據傳感器輸出值進行支架移動量控制。基于LabVIEW的礦用液壓支架姿態監測系統設計[18]是利用激光測距傳感器測量液壓支架底板與頂板的距離以及對支架頂板的姿態,實時顯示液壓支架的高度變化和頂板姿態變化。
上述研究工作均取得了一定的成果,但是還存在著一些問題:1) 在檢測工作面直線度的過程中沒有一個固定參考體系,只檢測到了自身的直線度,沒有檢測工作面與開采方向是否垂直,等等[19];2) 為了適應檢測方法,需要改造被檢測對象,需要在液壓支架上安裝大量的位置和姿態傳感器,這樣會造成大量前期改造費用和后續維護費用;3) 通過檢測相鄰支架位姿關系來推算所有支架位姿關系及直線度的方法,有一定的累積誤差[20];4) 對液壓支架進行6個自由度位姿檢測的研究尚未見文獻報道;5) LASC技術由于涉及軍工產品禁運及價格昂貴等問題,在國內的推廣使用受到一定的限制。
王國法[21]總結了基于支架相對位移的工作面直線度控制方法后認為:可以選取激光傳感器作為所有支架相對位移的參考,將其發射端安設在工作面的一端支架上,其他支架都安裝有接收裝置。每個支架的相對位置均與安裝有發射端的支架位置相比較,這樣工作面整體直線度就有一個統一標準。
1 液壓支架位姿檢測方法
1.1 支架位姿描述方法
描述剛體位姿的方法很多。本文借鑒描述船舶在航海時姿態的RPY角法,采用運動過程還原法對液壓支架的位姿進行描述。
一個剛體在空間有6個自由度,只要這6個自由度已知,則其在空間的位置和姿態就會唯一確定。設液壓支架群首架上固接的絕對坐標系為{H},待測支架上固接的相對坐標系為{S},則{S}系相對于{H}系的位姿可以這樣來描述:剛開始時兩個坐標系完全重合;經過了一系列復雜運動后{S}系到達了某一位姿。現在不考慮其具體運動過程,認為目前任何位姿都可以通過6次有序運動到達,即首先繞{H}系的X軸、Y軸、Z軸各旋轉一定的角度(θ,φ,ψ),再沿相應坐標軸各平移一定距離(u,v,w),最后到達了現在的位姿(如圖1所示),此時就可以分別用6個有序數列來表示這兩個坐標系。
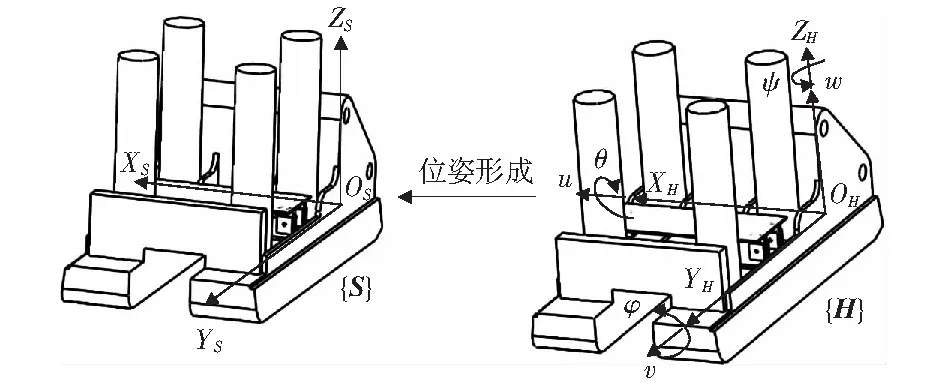
圖1 支架位姿形成過程示意圖Fig.1 Schematic of support pose formation process
設{H}系位姿為(0,0,0,0,0,0),則{S}系相對{H}系的位姿就可以表示為:
LOC(S,H)=(θ,φ,ψ,u,v,w) .
運動過程還原法采用從一個坐標系到另一個坐標系的6個運動參數來描述兩個坐標系的相對位姿,把運動和位姿有機地聯系起來,以便以后在三維虛擬環境下還原再現各液壓支架位姿和運行情況,從而進一步實現工作面支架位姿信息的透明化,并為調直支架直線度提供更全面的信息。
1.2 支架位姿檢測方法
綜上所述,本文提出了一種液壓支架位姿和直線度檢測方法模型,如圖2和圖3所示。
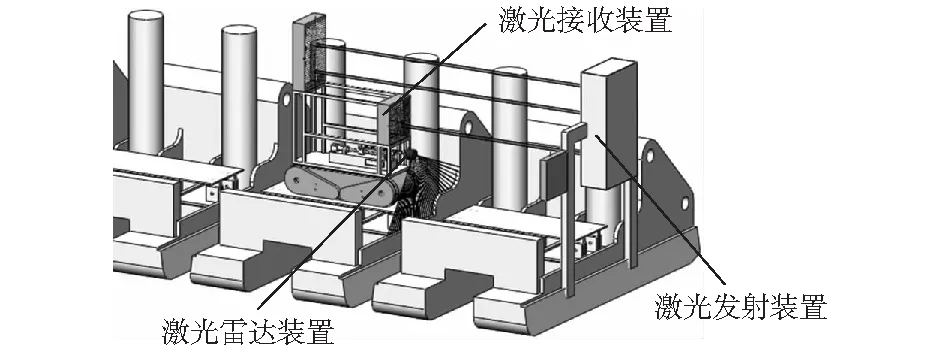
圖2 液壓支架位姿及直線度檢測三維模型Fig.2 3D model for measuring the pose and straightness of hydraulic supports
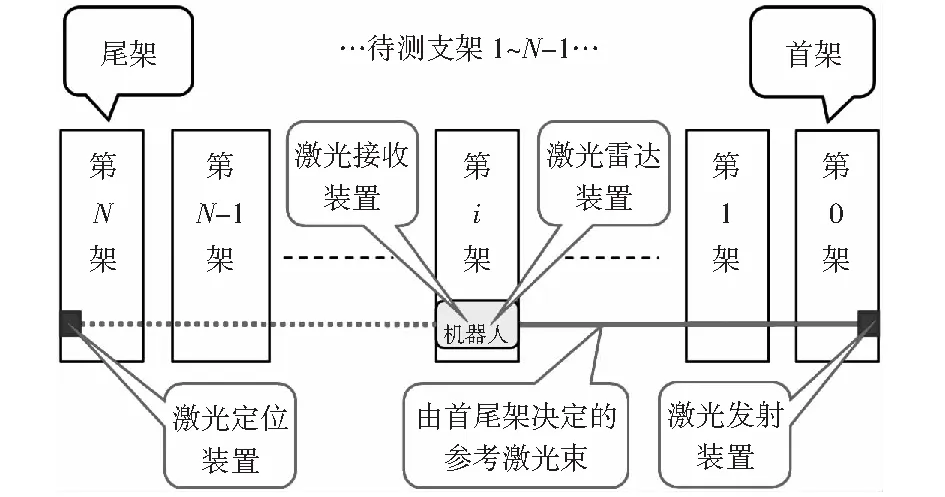
圖3 液壓支架位姿及直線度檢測平面模型Fig.3 Planar model for measuring the pose and straightness of hydraulic supports
該檢測模型選取工作面兩端支架作為所有支架的固定基準,其上各安裝一個激光發射裝置和激光定位裝置以形成一組固定的參考激光束。在一個巡檢機器人上安裝有一個激光接收裝置(檢測自身絕對位姿)和一個激光雷達裝置(檢測支架相對自身位姿)。機器人檢測液壓支架位姿及直線度的流程如圖4所示。
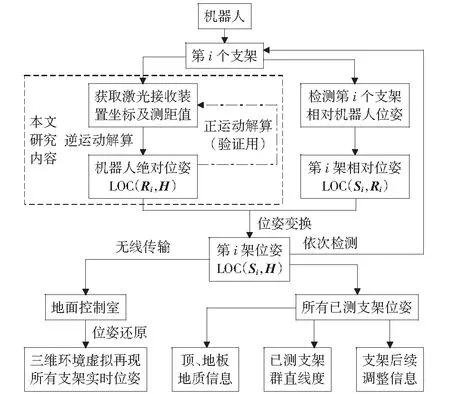
圖4 液壓支架位姿及直線度檢測流程Fig.4 Pose and straightness measurement process of hydraulic supports
設機器人坐標系為{R}.機器人行走在第i個支架人工行走平臺上時,采集自身攜帶的激光接收裝置坐標值及距首架的距離值解算出機器人絕對位姿(逆運動解算)為LOC(Ri,H)=(αi,βi,γi,ai,bi,ci);用激光雷達裝置檢測出待測支架相對機器人的位姿為LOC(SiRi)=(δi,εi,ζi,di,ei,fi);通過位姿轉換,得到第i個支架絕對位姿為LOC(Si,H)=(θi,φi,ψi,ui,vi,wi).完成位姿和直線度檢測后,把所有支架位姿信息實時傳輸給地面控制室,就可以在地面控制室還原井下所有支架的實時位置和姿態,并對如何調整支架位姿和支架群直線度做出決策[22]。
該檢測方法在基本不改造液壓支架結構的前提下,以激光束為統一參考基準,對支架位姿和直線度進行檢測,所獲得的直線度信息沒有累積誤差。另外,巡檢機器人還可以攜帶攝像頭及其他傳感器,給工作面外的人員提供視頻圖像和數據,以便他們及時了解工作面的情況。
1.3 巡檢機器人行走機構
行走在液壓支架上的機器人,除具備防爆防塵等要求外,其主要功能是能攜帶檢測裝置,識別和跨越兩個支架之間的溝壑,完成每個支架的位姿檢測。本文設計的巡檢機器人行走機構為六履帶四搖臂移動底盤。履帶機器人[23-25]結構簡單,故障率低,是煤礦理想的機器人行走機構,可以通過前后四個獨立搖臂與主體履帶的配合來越過支架之間的溝壑[26-27]。
本文主要以激光接收裝置和激光測距儀的檢測值為依據研究巡檢機器人位姿的檢測和解算。
2 巡檢機器人位姿檢測及解算
2.1 激光接收裝置結構設計及坐標系建立
本文將在前期激光定位矩陣研究[28-29]的基礎上,對激光接收裝置進行設計研究。
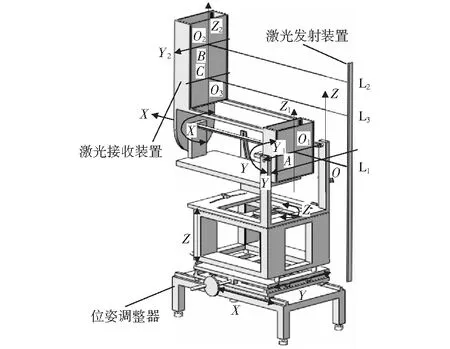
對于在液壓支架上行走的機器人,需要在其上安裝激光接收裝置,以便參考從首架發射的激光束來檢測自身位姿。如圖5所示,首架上安裝的激光發射裝置由兩個激光發射器L2、L3和一個兼有測距和發射激光兩種功能的測距儀L1組成。
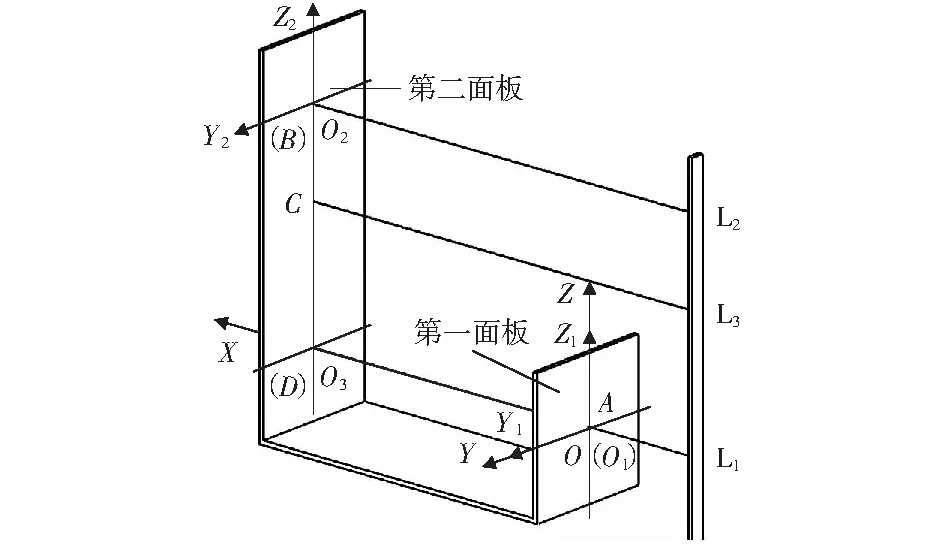
圖5 激光發射裝置和激光接收裝置結構模型Fig.5 Structural model of the laser launching device and the laser receiving device
將這三個儀器平行安裝在液壓支架群的首架和尾架(當機器人從首架向尾架移動時參考首架激光,反之參考尾架激光),且處于同一垂面,L1和L3相距300 mm,L2和L3相距200 mm.將激光接收裝置安裝在巡檢機器人上;該裝置由兩個平行的光敏電阻矩陣面板組成,兩者相距700 mm,前面低的為第一面板,后面高的為第二面板。當機器人在液壓支架上從首架向尾架移動時,激光接收裝置可以檢測到三束激光投射在兩個面板上的激光點的坐標,同時激光發射裝置檢測第一面板與其距離。
固定激光束是由激光發射器發射的散射度很小的點狀激光線形成,主要起著固定參考作用。激光接收裝置通過安裝在其上的若干個光敏電阻形成的矩陣來指示激光照射的坐標,從而確定其相對激光束在徑向的偏移量。
如圖5所示,在這個模型中共有三個坐標系,其中OXYZ為首架絕對坐標系{H},其余兩個為相對坐標系;O1X1Y1Z1為第一面板的坐標系{R},同時也是激光接收裝置和機器人坐標系;O2X2Y2Z2為第二面板坐標系{E},其與{R}系有固定位置關系;O3點是O1點在第二面板的投影點。現有三束激光沿X軸照射到這兩個坐標系上,由此可以獲得這三個激光束的坐標值。
A點是L1照射在第一面板上的光斑點,B,C兩點是L2和L3照射在第二面板上的光斑點,D點是L1與第二面板的虛擬交點。兩個面板上的激光接收裝置可以實時顯示檢測到的A,B,C點的坐標值。根據“六點定位原理”,只要有6個獨立的已知量就可以確定機器人在空間的位姿,即只需要A點的3個坐標值、B點2個坐標值、C點1個坐標值就可以把激光接收裝置(也就是機器人)的位姿唯一確定。
2.2 巡檢機器人位姿的逆運動解算
機器人上安裝的激光接收裝置所顯示的坐標可以理解為該裝置是從{H}系開始,經過3次旋轉和3次平移后得到的,其位姿解算過程就是根據激光接收裝置的坐標來逆向推算自身是經過了怎樣的3次旋轉和3次平移后到達該位姿。由于3次旋轉時,其結果與旋轉順序有關,因此本文認為機器人是經過了下面運動順序形成了最終的位姿:先依次繞X,Y,Z軸旋轉,再依次沿X,Y,Z軸平移。
2.2.1原始檢測數據
通過測距儀和激光接收裝置測到的坐標見表1.
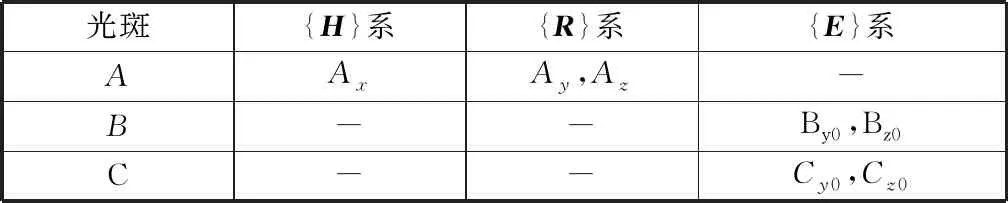
表1 可測得的A,B,C三點坐標Table 1 Measurable coordinates of A, B and C
表1中,Ax通過激光測距儀測得,Ay和Az通過激光接收裝置第一面板測得,By0,Bz0,Cy0和Cz0通過第二面板測得。
把B,C兩點坐標全部轉換到{R}坐標系中,則
RB=(700,By,Bz)=(700,By0,Bz0+500) ,RC=(700,Cy,Cz)=(700,Cy0,Cz0+500) .
式中,上標R表示選定的參考坐標系{R}.
根據“六點定位原理”,實際上只需要知道Ax坐標,再加上Ay,Az,By,Bz,Cy,Cz這6個坐標值中的5個就可以求解;另外一個相當于 “過定位尺寸”,其值的大小可以通過其他5個值表達出來。如果現在能多測出一個坐標值,就會給后面的計算帶來一些便利,也可以利用這個值對其他值進行驗算。
機器人從初始位姿(圖5)開始,首先繞X,Y,Z軸旋轉,旋轉的角度分別為α,β,γ,如圖6所示。其次再沿這三個坐標軸分別移動,移動的距離為a,b,c,如圖7所示。經過這樣的6次運動變換,形成了
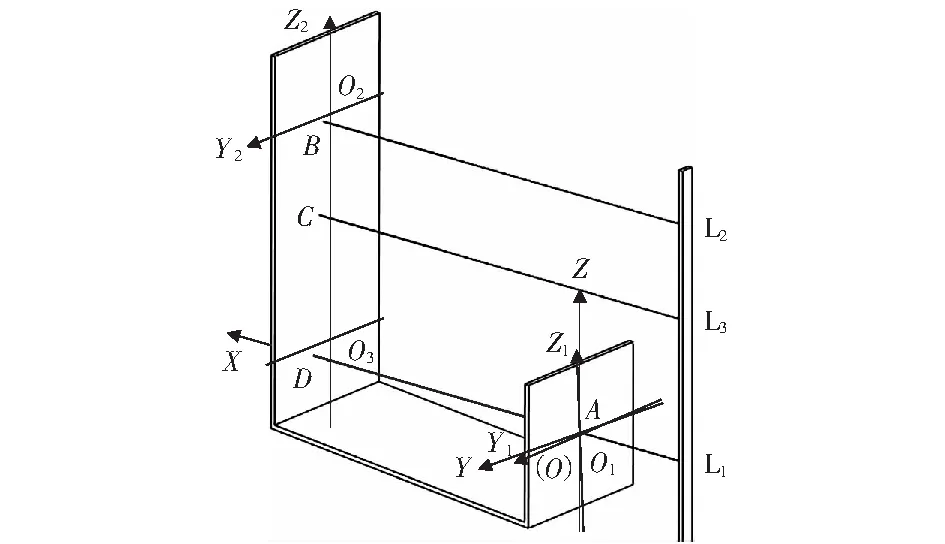
圖6 三次姿態變換Fig.6 Three changes of orientation
最后的位姿,位姿逆運動解算就是按照這個逆序進行還原求逆解。
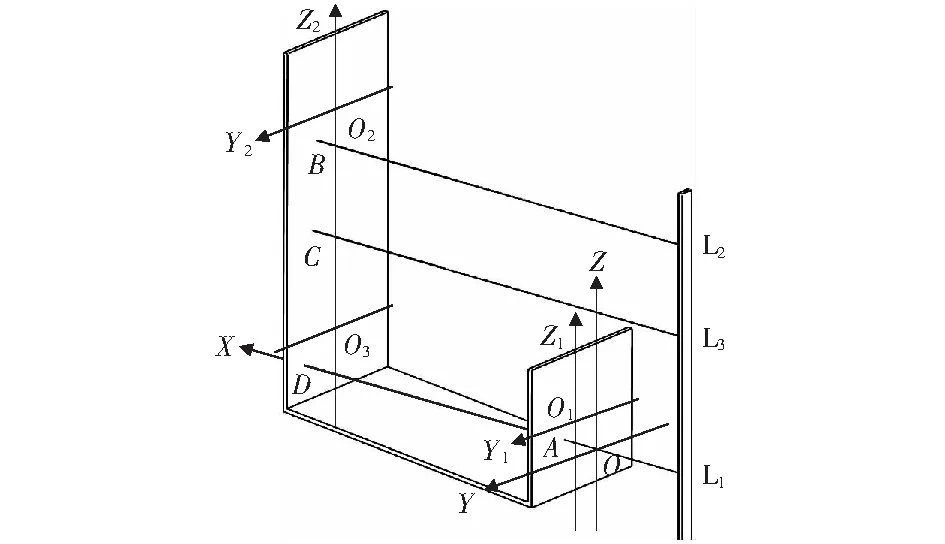
圖7 三次位置變換Fig.7 Three changes of position
2.2.2解算要點
位姿逆運動解算要遵循機器人運動的逆序進行還原,即先沿Z,Y,X軸逆向平移,再繞Z,Y,X軸逆向旋轉。即從圖7開始,最終將機器人上的激光接收裝置位姿還原為圖5的初始位姿。由于解算過程比較復雜,本文分四步對主要思路和步驟進行說明,詳細計算過程另撰文論述。
第一步,解算機器人沿X,Y,Z軸的平移值a,b,c.
采用坐標法求解a,b,c,具體原理如下。在{R}坐標系中,O1,A,B,D的坐標均為已知或可求;在{H}系中,A,B,D三點坐標也是已知或可求,需要求O1點坐標(a,b,c).根據同一線段在不同坐標中長度不變的原理,利用O1A,O1B,O1D三線段長度不變原理可得三個方程,解三個未知數,即為所求。
在{R}坐標系中,利用等比關系可以求出D點坐標:
RD=(700,Dy,Dz) .
其中
在{H}坐標系中,A,B,D三點坐標為:
HA=(Ax,0,0) ,HB=(Bx,0,500) ,HD=(Dx,0,0) .
其中,Ax為已知,Bx和Dx可由下式得出:
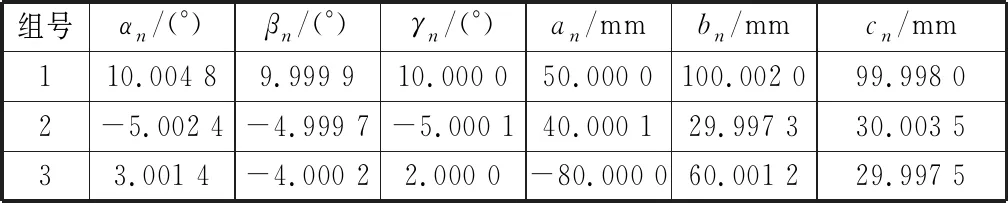
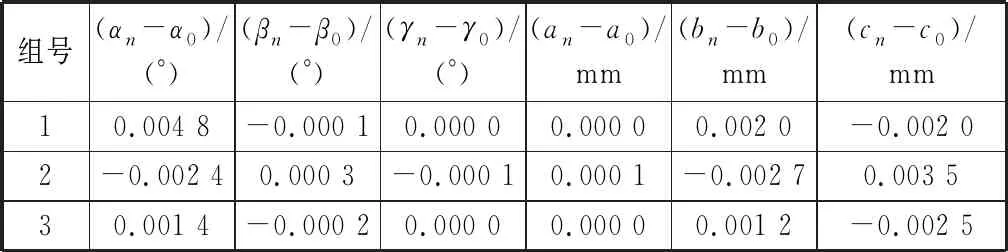
當Dz 綜上得O1,A,B,D四個點在兩個不同坐標系中的坐標,如表2所示。 表2 四個點在兩個不同坐標系中的坐標Table 2 Coordinates of four points in two different coordinate systems mm 列三個方程,解之得: (1) (2) (當Ay<0時取負號,Ay≥0時取正號) . (3) 根據求解結果進行相應的運動和坐標還原。在{R}坐標系內平移激光接收裝置使點A與點O1重合,則A,B,D三點在{R}坐標系中坐標還原為 RA=(0,0,0)=RO1,RB=(700,By1,Bz1)=(700,By-Ay,Bz-Az) ,RD=(700,Dy1,Dz1)=(700,Dy-Ay,Dz-Az) . 式中,坐標中的下標1表示還原次數,以下同。 在{H}坐標系內沿X軸方向平移激光接收裝置,使得O1和O重合,A,B,D三點在{R}坐標系中坐標不變,在{H}坐標系中的坐標還原為 HA=(0,0,0)=HO,HB=(Bx1,0,500)=(Bx-Ax,0,500) ,HD=(Dx1,0,0)=(Dx-Ax,0, 0) . 至此,激光接收裝置就還原為圖6所示狀態。 第二步,求激光接收裝置繞Z軸旋轉的角度γ. 采用幾何向量法進行計算。在{R}坐標系內,求過A,B,D三點的平面方程;然后求解B點在平面YOZ上的投影點E的坐標;再計算過E,A,O3三點的平面方程;兩平面ABD和EAO3的夾角即為γ. (當BD與Y軸交點Ey>0時取負號) . (4) 式中,A1,B1,C1和A2,B2,C2分別為平面ABD和EAO3方程的系數。 求解后,B和D點的坐標相應還原為 RB=(700,By2,Bz2) ,RD=(700,Dy2,Dz2) . 第三步,求激光接收裝置繞Y軸旋轉的角度β. 用幾何法求解得: (當Dz2>0時取負號) . (5) 求解后,D點坐標還原為初始值,B點坐標還原為 RB=(700,By3,Bz3) . 第四步,求激光接收裝置繞X軸旋轉的角度α. 用幾何法求解: (6) 求解后,B點坐標還原為初始值。激光接收裝置同時還原為圖5初始狀態。 需要說明的是,文中繞X,Y,Z軸旋轉的角度單位均為(°),沿X,Y,Z軸移動的距離單位均為mm. 綜上,α,β,γ,a,b,c這6個參數就組成了機器人在絕對坐標系內的位姿。也就是說,機器人相當于經過了這樣6次有序運動,從首架的初始位姿運動到了目前的位姿。 機器人的位姿計算完成后,需要對其正確性進行驗證。本文采用兩種方法進行驗證:一種是正運動解算法,另外一種是虛擬裝置運動模擬法。 機器人位姿逆運動解算需要A,B,C三個點的坐標值。因受激光接收裝置尺寸的限制,不能任意取值,所以設計驗證過程為: 1) 擬定機器人的運動過程(即機器人的位姿),如LOC(R0,H)=(α0,β0,γ0,a0,b0,c0). 2) 根據機器人運動過程,應用這兩種驗證方法分別得到A,B,C三點在{R}系的坐標Ay,Az,By,Bz,Cy,Cz和A點在{H}系的坐標Ax.如果結果相同,說明這兩方法都是正確的。 3) 把用這兩種方法得到的三個點坐標值代入位姿逆運動解算公式,還原機器人運動過程(機器人位姿),LOC(Rn,H)=(αn,βn,γn,an,bn,cn). 4) 比較LOC(R0,H)和LOC(Rn,H)的值,如果相同就說明機器人位姿的逆運動解算結果正確。 表3是擬定的三組機器人的原始運動過程數據 表3 擬定的三組機器人位姿Table 3 Proposed three sets of robot pose LOC(R0,H). 3.2.1正運動解算思路 正解算就是按照擬定的位姿參數,讓機器人從初始位置開始順序運動,從而追蹤激光接收裝置上A,B,C三個光斑點坐標的變化情況。即依照圖6和圖7運動順序,逐步計算機器人每次運動后坐標Ax,Ay,Az,By,Bz,Cy,Cz的值。 機器人上的激光接收裝置原始位姿如圖5所示,其上需要計算的各點初始坐標見表4.沒有列出的坐標為定值,由裝置結構決定,在機器人運動過程中不發生變化。 表4 A,B,C三點初始坐標Table 4 Initial coordinates of point A, B, C mm 3.2.2正運動解算過程要點 機器人每運動一步,相應三個點的坐標值都可能有變化,所以本文僅對每一步的計算要點進行說明,略去了部分具體表達式。 第一步,繞X軸旋轉α. 激光接收裝置形成了新的位姿,在{R}坐標系中,有以下坐標發生了變化: By1=500sinα,Bz1=500cosα,Cy1=300sinα,Cz1=300cosα. 第二步,繞Y軸旋轉β. 在{R}坐標系中,形成了以下新的坐標: 第三步,繞Z軸旋轉γ. 同理,在{R}坐標系中,形成了以下新的坐標:By3,Bz3,Cy3,Cz3. 第四步,沿X軸平移a. 在{H}坐標系,Ax坐標發生改變,其余坐標無變化。 Ax4=a. 第五步、第六步,沿Y軸平移b,沿Z軸平移c. 在{R}坐標系,形成了以下新的坐標:Ay6,Az6,By6,Bz6,Cy6,Cz6.在{H}坐標系,形成了以下新坐標:Ax6. 最后,把B,C兩點沿Z軸坐標轉換到{E}系內: Bz7=Bz6-500 ,Cz7=Cz6-500 . 綜上,Ax6為激光測距儀應檢測的距離值;Ay6,Az6為第一面板應顯示的坐標值;By6,Bz7,Cy6,Cz7為第二面板應顯示的坐標值。 根據正運動解算公式,對表3的運動數據進行計算,得到表5的結果。該值為激光測距儀應測出的A點理論距離值和激光束L1,L2,L3落在激光接收裝置上的光斑點A,B,C的坐標值。 表5 根據擬定位姿進行的正運動解算結果Table 5 Rusults of positive motion calculation using the proposed robot pose mm 圖8是在Solidworks三維機械設計軟件里建立并裝配的位姿調整器、激光發射裝置及激光接收裝置虛擬模型。安裝了激光接收裝置的位姿調整器可以模擬機器人經過六次運動調整后,從初始位姿到達最終位姿后激光束在兩個面板的坐標變化情況。把原始運動過程數據依次代入,然后測量在兩個坐標面板上三個點的坐標值,就得到模擬運動的結果,該值應該與正解算結果相同。該模擬方法不需要計算公式,能真實展現激光接收裝置的實際運動過程,把運動過程和位姿結果直觀地聯系了起來。 表6是根據表3的運動數據進行的三維虛擬裝置運動模擬測量結果。 圖8 用SolidWorks軟件建立的位姿調整器、激光接收裝置 和激光發射裝置三維模型Fig.8 3 d models of pose adjuster, laser receiving device and laser launching device established with SolidWorks software 表6 根據擬定位姿進行的虛擬裝置運動模擬結果Table 6 Motion simulation results of 3D digital virtual device using the proposed robot pose mm 正運動解算和三維虛擬裝置運動模擬兩種驗證方法的結果比較如表7所示。從表中可以看出,兩種方法得出的結果有一定的誤差,這是由于正運動解算過程和軟件模擬計算過程不盡相同,但誤差均非常小,可以忽略不計。 表7 正運動解算與虛擬裝置運動模擬結果比較Table 7 Comparison of positive motion calculation and virtual assembly motion simulation mm 表8是根據表5進行的機器人位姿逆運動解算結果。由于三維虛擬裝置運動不能進行位姿逆運動模擬,所以只有正運動模擬結果。 表9是擬定位姿與逆運動解算位姿比較的結果。從表中可以看出,機器人位姿理論計算是完全正確的,而且具有唯一性,誤差屬于正常范圍,可以忽略不計。 表3、表5-表9是從大量驗證數據中摘錄的三 表8 根據表5計算的機器人位姿逆運動解算結果Table 8 Robot pose solved by using the inverse motion formula according toTable 5 表9 逆運動解算位姿與擬定位姿比較Table 9 Comparison of inverse motion solution and the proposed robot pose 組數據,這三組數據基本代表了該裝置的測量范圍和檢測特征。巡檢機器人位姿檢測理論和逆運動解算的正確性,為后續液壓支架姿態及直線度檢測和調整實驗研究奠定了基礎。 1) 提出了描述液壓支架6個自由度位姿(3個位置自由度(u,v,w)和3個姿態自由度(θ,φ,ψ))的運動過程還原法。基于該方法,設計了利用巡檢機器人對液壓支架位姿和直線度進行檢測的方法模型。該檢測模型先利用激光接收裝置檢測巡檢機器人位姿,再用激光雷達裝置檢測待測支架相對機器人位姿,最后通過位姿轉換獲得各支架位姿,進而再計算出整個支架群的直線度。用該方法模型檢測支架位姿,不用在待測支架上安裝任何傳感器,計算得到的直線度沒有累積誤差。 2) 探索了利用激光束、激光測距儀和激光接收裝置對機器人位姿進行檢測的裝置結構及尺寸。通過分析裝置和建立坐標系,推導了機器人位姿的逆運動解算公式,實現了機器人位姿的運動過程還原。該機器人位姿檢測方法只利用激光接收裝置上3個點的6個坐標值來計算機器人的3個位置坐標和3個姿態角度,這為其他場合的位姿檢測提供了理論依據。 3) 通過正運動解算和虛擬裝置運動模擬兩種方法驗證了巡檢機器人位姿檢測的逆運動解算的正確性,這為后續液壓支架姿態及直線度的檢測和調整實驗研究奠定了基礎。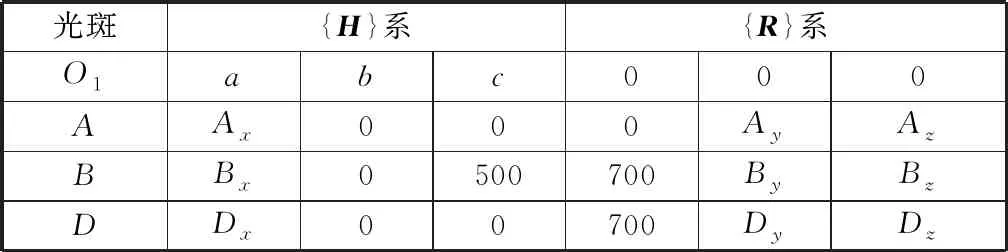
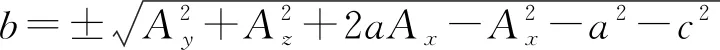
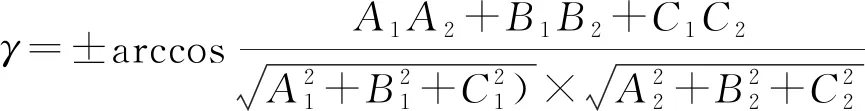
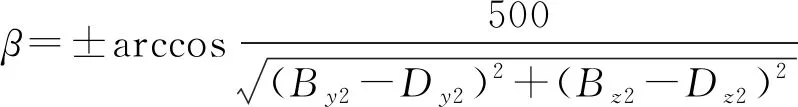
3 巡檢機器人位姿解算結果驗證
3.1 驗證過程設計

3.2 正運動解算法驗證


3.3 虛擬裝置運動模擬法驗證

3.4 驗證結果分析

4 結論

