基于PSO-BP神經網絡的地鐵盾構場地土體參數反演

郭子奇，楊雙鎖，李彥斌，2，楊歡歡，龐 星，羅百盛

(1.太原理工大學 礦業工程學院，太原 030024；2.中國礦業大學 深部巖土力學與地下工程國家重點實驗室， 北京 100083；3.中鐵三局集團有限公司，太原 030001)

地下空間的開發利用可以緩解用地緊張、交通擁擠以及環境污染等難題，同時具有災害發生時的物資儲備倉庫、安全通道等作用。在21世紀，由于人口和各類生產要素的加速積累，地下空間的開發利用必將迎來高峰。利用數值計算方法對地下工程進行工況模擬以驗證工程的穩定性，是提高地下工程安全性的重要措施。因此，準確的土體參數是保證數值模擬計算正確性的前提條件[1]。

巖土工程數值模擬中，幾乎所有的計算都不可避免地要進行參數調整，且參數調整主要集中在土的參數[2]。其原因可能為：1) 巖土體本身以及所處介質的相互作用的復雜性，使得室內試驗或現場原位測試無法精確獲得土體的物理力學參數；2) 巖土勘察能夠確定的參數有限，大多數勘察也是以點代面，因此參數的準確性難以保證；3) 在隧道的建設中需進行注漿以加強支護，而漿液的擴散會改變周圍土體的物理力學參數。因此，進行土體參數反演成為一種為數值分析提供符合實際的土體參數的有效方法。

迄今學者們對參數反演已進行了大量的研究。周建春等[3]采用BP神經網絡對公路隧道新奧法施工過程中圍巖力學參數進行了反演分析，但針對的是單層圍巖的參數。張志華等[4]對鄭州地鐵工程進行了土體參數敏感性分析和BP神經網絡的參數反演，證明了參數反演方法的可行性。張海洋等[5]采用數值模型模擬了木寨嶺隧道大戰溝斜井試驗洞的開挖蠕變過程，建立了BP神經網絡并驗證了該神經網絡的可行性。

從現有的研究來看，BP神經網絡進行參數反演的精度可以滿足工程需要，但在算法的進行過程中存在計算時間長、效率低、收斂慢、全局搜索能力差、易陷入局部最優解等缺點[6]。因此，本文在BP神經網絡的基礎上引進粒子群算法(PSO)，以期提高參數反演的全局優化性和收斂速度。此外，綜合前人文獻發現，由于土體參數的地域性特點，以往文獻所得結論并不能適用于其他的地區。本文針對太原地區的代表性土層進行研究，以期對同地區的巖土工程提供參考。

1 PSO-BP神經網絡參數反演方法

人工神經網絡是一種應用類似于大腦神經突觸聯接的結構進行信息處理的數學模型。這種網絡依靠系統的復雜程度，通過內部大量節點之間的相互連接關系的調整，來達到相應的信息處理的目的。

BP神經網絡即反向傳播(back-propagation network)，是人工神經網絡最精華的部分[7]，其模型結構如圖1所示。

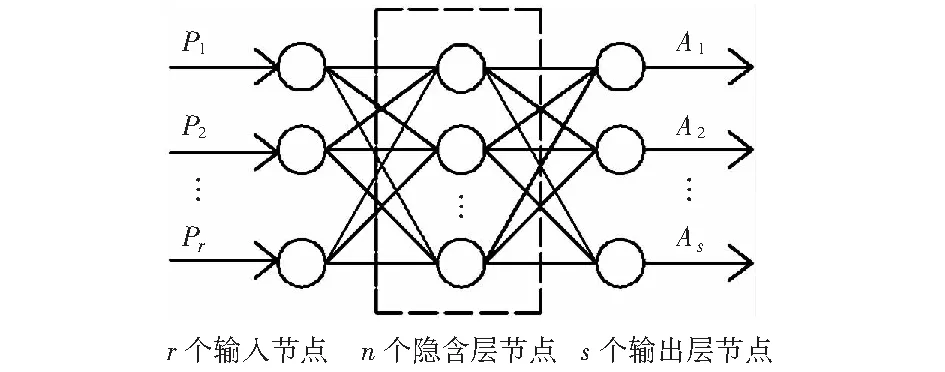
圖1 BP神經網絡結構Fig.1 Structure of BP neutral network

粒子群算法(particle swarm optimization，PSO)是進化算法的一種，由隨機解出發，通過迭代尋找最優解。與前人利用遺傳算法對BP神經網絡進行的改進相比，粒子群算法的規則更加簡單，沒有遺傳算法中的“交叉”和“變異”操作。它通過追隨當前搜索到的最優值進行全局最優的尋找，具有實現容易、收斂快、精度高的優點。利用PSO-BP神經網絡進行反演的流程如圖2所示。

圖2 PSO-BP神經網絡土體參數反演流程Fig.2 Flowchart of back analysis for soil parameters based on PSO-BP neutral network

反演步驟具體如下：

1) 獲得實測資料。在地鐵的施工現場布置測點，并獲得相關測點對應的實際地表沉降量。

2) 進行正演。首先，通過地勘資料確定土體物理力學參數的范圍，并進行參數的組合設計。然后通過有限差分軟件建立數值模擬模型，得到與實際地表沉降監測點相同位置的沉降量。

3) 進行參數反演。首先，建立并訓練神經網絡：初始化BP神經網絡，設定其參數；設定粒子群的種群規模、維度以及隨機產生的粒子的速度與位置；計算每個粒子的適應度；比較適應度，確定粒子的個體極值點與全局最有極值點；更新粒子的速度與位置；查看其迭代次數與誤差是否達到精度要求。之后，根據實際監測得到的地表沉降值，利用訓練好的PSO-BP神經網絡進行參數反演。

4) 驗證反演參數的正確性。將反演得到的參數代入數值模擬模型中，將模擬的地表沉降值與實際監測得到的地表沉降值進行對比，以驗證參數反演的正確性。

2 PSO-BP神經網絡的建立

2.1 工程概況與數值模擬模型的建立

本文以太原地鐵二號線某區間為背景依托工程。該區間屬汾河東岸一級階地，距汾河約2.0 km，地勢平坦，南低北高，地面標高約為781.8～782.6 m.根據鉆探結果，該區間地層分布較為穩定，均為第四系(Q)地層覆蓋。地表多為第四系人工填土，其下多為粉質黏土、粘質粉土及中砂。該區間管片厚度350 mm，管片環寬1 200 mm，隧道內凈空直徑為5 500 mm，地鐵區間隧道外徑6.2 m，隧道拱頂埋深為10.1～15.6 m，左右線間距為15.7～14.2 m，是典型的漫灘地帶[8]。

根據地勘資料，以兩隧道中心連線為原點建立數值模擬模型，如圖3所示。模型長度選取以影響范圍不波及邊界為原則。根據圣維南原理，影響范圍約為開挖范圍的3～5倍[9]，因此所建立的模型尺寸為75.0 m×24.0 m×31.5 m(長×寬×高)。將

圖3 盾構隧道三維模型Fig.3 3D model of the shield tunnel

數值模擬模型中土層由上至下概化為表1.

表1 模型概化土層分布Table 1 Distribution of simplified soil layers of model

隧道拱頂埋深取15.5 m，隧道間距取15.4 m.管片采用shell單元，彈性模量為34.5 GPa，泊松比為0.3.在盾尾注漿的過程中，漿液與土體相互滲透，在空隙中形成一圈過渡圈層，稱之為等代層，以此來模擬注漿量的大小。本模型根據實際施工，取等代層的彈性模量為4.5 MPa，泊松比為0.35.模型上表面為自由邊界，其余邊界均固定。模型除注漿采用彈性模型外，其余皆采用庫倫摩爾模型。施工時首先挖空左隧道，再挖空右隧道。在隧道開挖時，首先開挖1 200 mm(一個管片的長度)，然后安裝管片，之后進行同步注漿，最后再挖空下一環。循環往復，直至兩個隧道都被挖空。

2.2 正交試驗設計

土層涉及的物理力學參數有很多，例如彈性模量E，泊松比μ，內聚力c，內摩擦角φ，等等。若對每一個參數都進行參數反分析，則工作量太大，計算過程困難，因此可以根據不同參數對土體沉降的影響大小，選取兩個主要因素進行分析。由文獻[10]可知彈性模量E、內摩擦角φ為兩個最敏感的因素。因此，本文選取彈性模量E和內摩擦角φ作參數反演。根據地勘資料，彈性模量和內摩擦角的取值范圍如表2所示，共6個因素，5個水平。若進行全面試驗，則需要進行56=15 625次試驗，耗時費力。因此，采用正交試驗法進行試驗，選用5水平6因素正交表(L25(56))確定不同參數的組合方式，共25次試驗。

表2 計算選用參數Table 2 Values of parameters for calculation

2.3 PSO-BP神經網絡參數的確定

2.3.1輸入層和輸出層

由2.2部分可知，共取三個土層，對每層土的兩個參數進行反演，所以輸出層的節點數m=6.根據實際地鐵施工的監測數據，本文選取兩隧道頂部及兩隧道連線中心3個點為監測點，則輸入層節點數n=3.

2.3.2隱含層

一個神經網絡可以有許多層。根據研究，一個隱含層的神經網絡足以表達任意精度的映射關系，因此本文選取一層隱含層。隱含層的神經元數由經驗公式(1)來確定：

(1)

式中：n1為隱含層神經元數，m為輸出層節點數，n為輸入層節點數，a為1～10的常數。

2.3.3編碼長度

編碼長度N的計算公式如下：

N=n×n1+n1+n1×m+m.

(2)

3 參數反演過程

本文中BP神經網絡中輸入層的節點數n=3，輸出層的節點數m=6，隱藏層的節點數n1=5.則編碼長度N=6×5+5×3+3+5=53，粒子維數D為53維，種群規模取40，學習因子c1為2，c2為2，最大速度v為0.5，最大迭代次數Tmax=200.

神經網絡傳遞函數采用tansig函數，輸入層函數采用purelin函數。

神經網絡計算模型結構如圖4所示。

根據2.2部分的正交實驗法，進行25組模擬實驗，得到的數據如表3所示。

圖4 BP神經網絡計算模型結構Fig.4 Structure of BP neutral network for calculation

表3 神經網絡計算樣本Table 3 Neutral network training samples

將地表沉降量作為輸入值、參數作為輸出值，代入到神經網絡進行訓練。取目標函數為計算位移與檢測位移的差值的平方和，利用PSO-BP算法去跟蹤目標適應度值的變換；反復更新迭代次數，使得最小誤差值減小至規定的精度內，來取得最優值。粒子群算法的最優個體適應度隨迭代次數的變化如圖5所示。

將實際地表沉降量(左隧道頂、兩隧道連線中心和右隧道的沉降量分別為-1.274，-1.452，-1.256 cm)代入到已經訓練好的PSO-BP神經網絡中，得到各土層的彈性模量和內摩擦角分別為：雜填土層11.25 MPa，12.60°；粉質黏土層15.90 MPa，30.60°；中砂層13.30 MPa，25.20°.

將得到的參數代入到下一工況模擬模型中。將PSO-BP神經網絡模擬、BP神經網絡模擬、原狀土測得的參數模擬所得地表沉降量與實際地表沉降量進行對比，結果如表4和圖6所示。

圖5 PSO-BP算法迭代曲線Fig.5 PSO-BP algorithm iteration curve

由表4和圖6的結果可以看到：利用原狀土的地勘資料進行模擬所得的地表沉降值與實際沉降值相差較大，最大誤差達到18.9%，整個沉降曲線與實際擬合效果較差；BP神經網絡反演出的模型誤差在工程應用的允許范圍之內(誤差<10%)；PSO-BP神經網絡改善了BP神經網絡易陷入局部最優值的缺點，誤差更小，準確性和精度相對更高，對工程的指導意義很大。

由表4還可看出，在隧道右側模擬所得數值與實際所監測的數據相差較大。分析其原因，可能如下：由于數值模擬模型是以實際地形中隧道連線中心截面而建立的，土層在同一水平上是一樣的；而在實際開挖過程中，土層分布可能并不一致，導致了誤差的出現；但在土層參數取點附近的模擬沉降值與實際監測所得沉降值很接近。

表4 數值模擬結果與實測位移數據對比Table 4 Comparison of the calculation and monitored displacement

圖6 數值模擬結果與實測位移對照曲線Fig.6 Comparison curve of the calculation and monitored displacement

總體上說，PSO-BP神經網絡參數反演方法正確，反演精度較高，反演出的土體物理力學方法有較高的可信度，可以利用反演出的參數對下一工況進行預測或為類似工程提供借鑒。

4 結論

本文利用正交法和PSO-BP神經網絡，結合有限差分軟件FLAC3D，對太原地區盾構施工場地進行了參數反演，得到了以下結論：

1) 通過參數反演分析，得到各土層的彈性模量和內摩擦角分別為：雜填土層11.25 MPa，12.60°；粉質黏土層15.90 MPa，30.60°；中砂層13.30 MPa，25.20°.

2) 基于正交設計建立的PSO-BP神經網絡模型具有較高的精度，能夠較好地反映地表變形與土體各參數之間的非線性關系，且避免了局部最優解，計算精度比BP神經網絡有所提高。

3) 利用反演得到的參數計算的地表位移變形情況與現場實際監測值相對誤差較小，模擬情況符合實際施工情況，說明該方法有效合理，可為后續施工和類似工程提供借鑒參考。