橋梁應變采集系統設計及溫度效應研究

王 煜，李艷萍，張 博，呂立程，宋相榮

(太原理工大學 信息與計算機學院 微納系統研究中心，教育部新型傳感器與智能控制系統重點實驗室，山西 晉中 030600)

應變監測是橋梁結構健康監測中的一項重要內容。通過對橋梁應變數據的分析，可以實現對橋梁結構的安全預警以及狀態評估[1]。傳統的橋梁應變數據采集儀基于485通信協議的測量方式，接線量大且復雜性高，采集效率低下且誤差較大，嚴重影響了應變采集系統的可靠性[2]。目前應變采集中最常用的振弦式應變計具有結構簡單、靈敏度高、抗干擾能力強、適合長距離傳輸等優點，但在工程的實際應用中，測量點多且數據量大，故單一的振弦式應變計模塊很難滿足需求[3]。因此，研發采集效率高、測量誤差小、可滿足多個振弦式應變計同步測量的橋梁應變采集系統具有十分重要的意義。

鑒于此，本文設計了一款基于FPGA的振弦式應變計數據采集系統，可同步采集8路振弦式傳感器數據。同時針對傳統測頻方法中測頻精度受被測信號頻率影響的問題，采用了等精度測量法。最后該系統依托山西省晉蒙黃河大橋進行實地實驗，研究溫度對橋梁應變的影響，以求得到更加準確的應變數據。

1 基于FPGA的應變采集系統設計

由于FPGA芯片擁有較多的片內RAM資源，相比于DSP和ARM擁有更快的數據處理速度、更加豐富的引腳資源以及出色的并行處理能力[4]。因此，在本次設計中選用Xilinx公司的Spartan6系列FPGA作為控制芯片。

系統采集模塊共由3部分構成：檢測電路、激振電路和拾振電路。檢測電路主要利用振弦式傳感器兩線之間具有固定電阻的特點，來檢測振弦式傳感器的連接情況。激振電路為振弦式應變計提供激勵信號，使傳感器起振。拾振電路對傳感器傳回來的信號作濾波、放大處理，并且為了頻率計的檢測，將信號整形為方波。采集模塊在實現功能時，不同的電路需要在不同的時間分別與傳感器連接，因此需要設計一個電路實現不同時間選通相應電路與傳感器連接。由于在切換電路連接時，有3個電路要分別與振弦式傳感器相連，故多路選擇器選通通道要大于等于3路，因此本系統選用ADG1609多路選擇器，其內部集成了兩組多路開關，片上的A0和A1為數據選擇引腳，可以通過對其引腳A0和A1的編碼實現s1A-s4A中的某一引腳與DA導通，以及實現s1B-s4B中的某一引腳與DB導通。故ADG1609多路選擇器可達到信號切換的目的。

系統上電后，首先通過多路選擇器將檢測電路與振弦式傳感器相連，檢測傳感器是否連接到系統上，當檢測到傳感器已接入后，執行下一步操作，通過多路選擇器將激振電路與傳感器相連，給傳感器提供激勵信號，以使傳感器內的鋼弦起振[5]。激勵結束之后，將系統切換至檢測模式，將傳感器與檢測電路連接，對傳感器輸出的信號進行濾波、放大整型后傳給頻率計，檢測計算傳感器的頻率值。整體設計框圖如圖1.

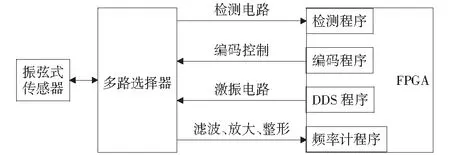
圖1 整體設計框圖Fig.1 Overall diagram of system

1.1 檢測電路設計

在對傳感器提供激勵信號前，需檢測傳感器是否連接到系統上，以免在傳感器未連接時提供激勵產生不必要的功耗或檢測出錯誤數據的影響，檢測電路如圖2所示。

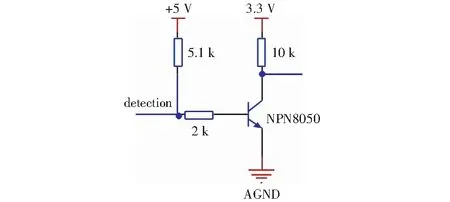
圖2 檢測電路Fig.2 Detection circuit

1.2 激振電路設計

在采集振弦式應變計頻率信號之前，需要使振弦式傳感器起振，因此需設計激振電路。本系統選用ADI公司的AD9833芯片[6]來輸出掃頻信號，該芯片是一款低功耗、高精度、可編程波形發生器，是一塊完全集成的DDS電路。通過FPGA控制DDS芯片(AD9833)輸出頻率為400～5 000 Hz的方波信號。AD9833電路如圖3所示。

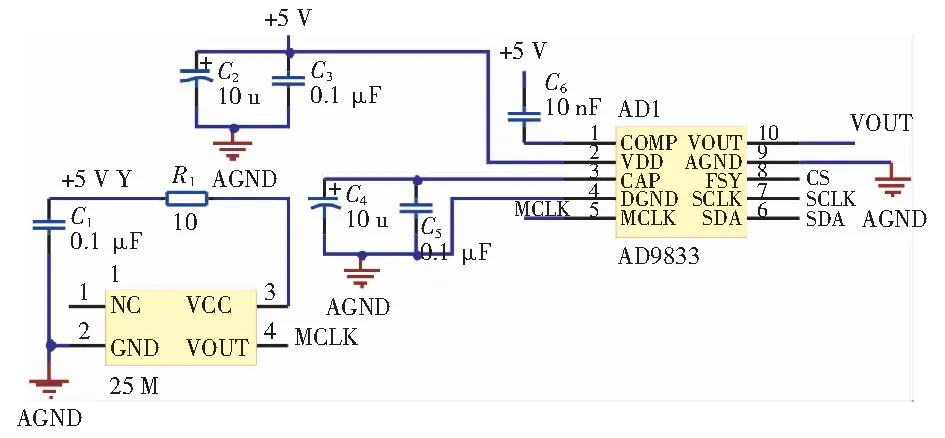
圖3 AD9833電路圖Fig.3 Circuit diagram of AD9833

在電路中，AD9833的MCLK引腳與一個25 MHz的晶振相連接，為AD9833提供頻率參考，FSY、SCLK、SDA等3個引腳與FPGA相連接，通過FPGA控制DDS芯片輸出需要的波形頻率。

由于AD9833輸出電流較小，直接作用于傳感器不會使鋼弦共振或振動幅度很小，因此需將信號進行放大。放大之后，通過兩個二極管將輸出波形整形為方波。電路如圖4所示。

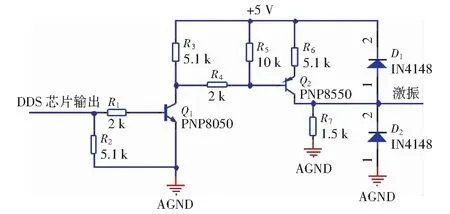
圖4 激振電路Fig.4 Excitation circuit

1.3 拾振電路設計

激振電路完成激勵后，將多路選擇器切換至拾振狀態，由于傳感器輸出信號電壓的電流較小，而且容易受到周圍信號的干擾，為了提升測量的準確度，需在FPGA測頻[7]之前對傳感器輸出信號進行放大濾波處理。由于振弦式傳感器的固有頻率范圍在400～5 000 Hz之間，綜合上述情況，選用帶通濾波器，電路如圖5所示。

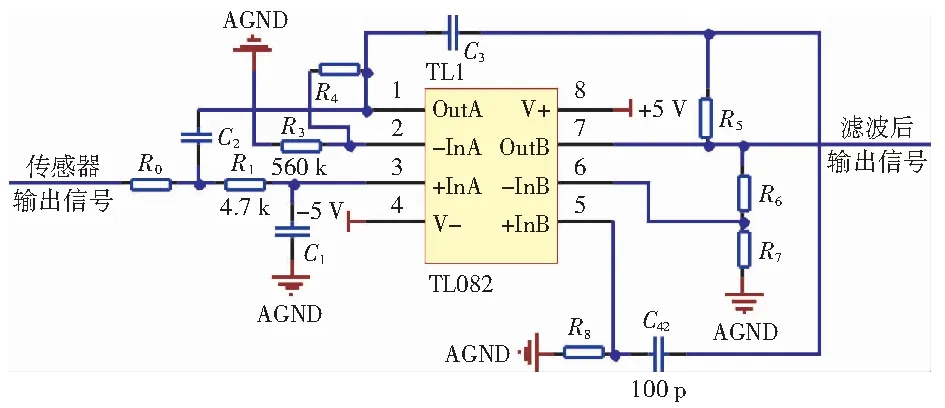
圖5 濾波放大電路Fig.5 Filter amplifier circuit

2 測頻方法

目前常用的測頻方法有直接測量法和周期測量法。直接測量法以固定時間t為基準，計數時間t內被測信號的脈沖數N，然后用公式N/t求出單位時間內的脈沖數，通過此方法計算的結果即為被測信號的頻率。周期測量法與直接測量法不同，是計算被測信號的周期T，然后根據公式f=1/T求解計算被測信號的頻率。這兩種方法具有原理簡單、易于實現的優點，但對于被測脈沖計數會產生±1的誤差。對于頻率比較低的信號，周期測量法精度比較高；對于頻率比較高的信號，直接測量法比較適合。但是，對于未知的信號，無法知道其頻率大小，這兩種方法不能滿足對高低頻率等精度測量的要求[8]。因此，為兼顧對高低頻率的測量，本文采用了一種等精度測量法。

2.1 等精度測量法原理

等精度測量法與其他測量方法最大的區別是門控時間不是以基準時鐘為基準，而是與被測信號有關，它不是一個固定值，是被測信號的整數倍。測量過程中，對被測信號和基準時鐘都要進行計數，再通過計算得到被測信號的頻率值。原理如圖6.

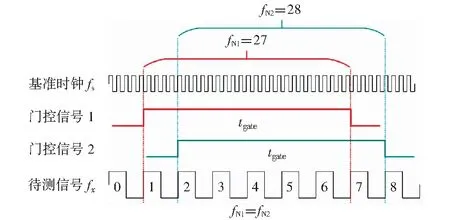
圖6 等精度測量原理圖Fig.6 Schematic diagram of equal precision measurement

圖6中，fs代表基準時鐘頻率，tgate代表門控信號時間，fx為待測信號頻率。等精度測頻法在計算上升沿個數時，對基準時鐘周期的誤差為±1，得到公式(1).

ΔfN=±1 .

(1)

tgate的時間在數值上等于脈沖個數fN乘以基準時鐘的周期(即基準時鐘頻率的倒數，基準時鐘頻率用fs表示)，通過計算可以得公式(2).

(2)

推導得

(3)

又由于待測信號頻率值在數值上等于待測信號在tgate時間內的脈沖個數除以tgate的時間值，故通過計算得到公式(4).

(4)

所以

(5)

通過以上公式推導可得，等精度頻率計的測量方法相對誤差取決于基準時鐘頻率的大小，而與被測信號的頻率大小無關，解決了由被測信號頻率大小影響的誤差問題。

2.2 等精度測量法的FPGA實現

本文結合FPGA技術，利用Verilog硬件描述語言設計實現了一種數字等精度頻率計，測頻模塊RTL圖見圖7.

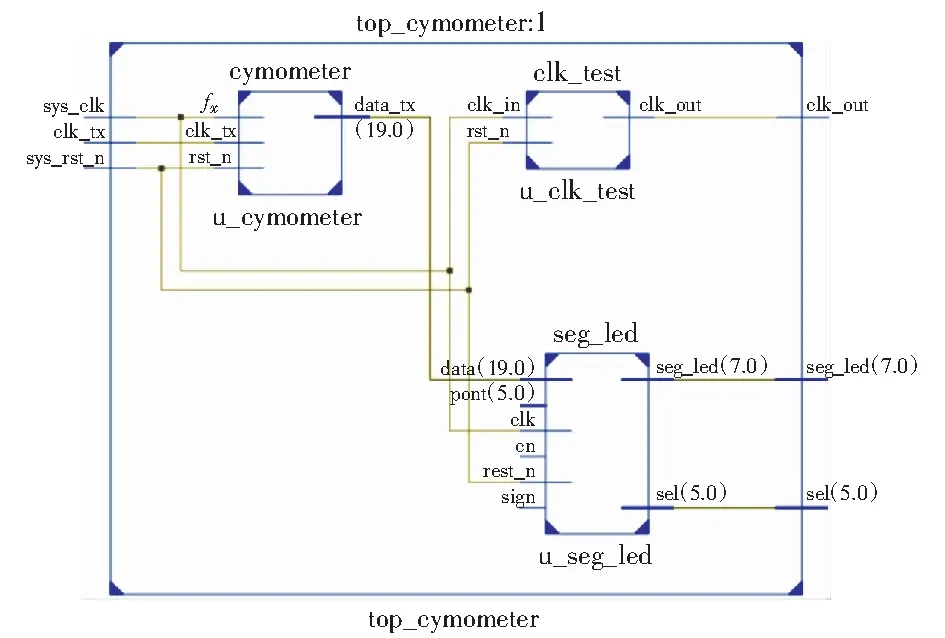
圖7 測頻模塊RTL圖Fig.7 RTL diagram of frequency measurement module

圖7中，左上角的cymometer模塊為測頻模塊，fx為被測信號輸入引腳。Seg_led用于將計算出的被測信號頻率值顯示到電路板上的LED數碼管模塊上。

在設計測頻模塊程序時，輸入輸出端口定義了3個wire類型的輸入信號，分別用于提供基準時鐘信號、復位信號和被測時鐘信號，還有一個寄存器類型的輸出信號，用于被測時鐘頻率信號數據的輸出。此外，定義了一個參數fs，用來表示基準時鐘頻率值。而且通過定義兩個局部參數wmax和tgate，分別用于表示fs,N和fx,N的最大位寬以及門控時間的設置。其中fs,N代表門控時間內基準時鐘的計數值，fx,N代表門控時間內被測時鐘的計數值。

3 系統測試

設計完成的振弦式應變計橋梁應變采集系統如圖8所示。相較于傳統的應變數據采集儀，具有測量精度高、采集效率高、接線簡單等特點。并可接入8路振弦式應變計進行同步測量，在橋梁的實際應用中可以布設一個大的應變傳感網絡來對整個橋梁進行覆蓋。

圖8 橋梁應變采集系統實物圖Fig.8 Design of bridge strain acquistion system

在實驗室環境下，使用標準應變源對比測試的部分結果如表1所示。測試表明本系統的測量誤差低于2%，達到工程應用所需標準。

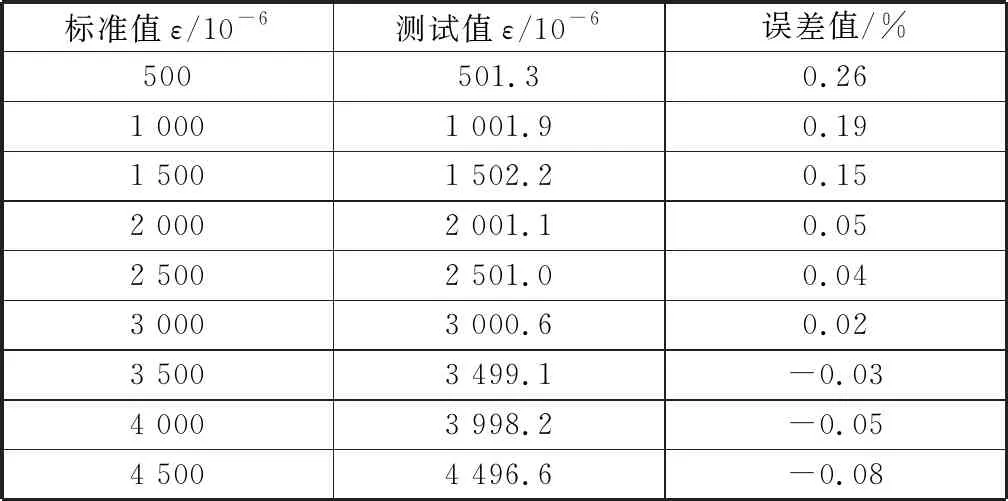
表1 應變數據測試對照表Table 1 Comparison of strain data test

4 應變監測數據的溫度效應研究

在實際運營過程中，橋梁結構除了受到車輛荷載的作用之外，還會受到復雜溫度場的影響，然而人們在對橋梁應變進行分析的過程中，往往只考慮車輛荷載效應，從而忽略了溫度效應[1]。因此，若能找到應變值和溫度值之間的關系，即可通過對應變進行溫度補償來得到更加準確的應變數據，在橋梁健康監測中具有重要意義。

本文依托山西省晉蒙黃河大橋，通過對橋梁的現場分析(橋主梁采用變截面連續梁，具有大的縱向斜度)，制定了晉蒙黃河大橋應變及溫度測量點的布設方案。選取主橋重載車幅為監測跨，應變傳感器布設截面為所選監測跨的跨中位置[9]。

在確定應變和溫度之間的關系時，回歸函數是未知的，需要根據實測的溫度和應變值估算函數，并討論與之相關的統計推斷。要解決的基本問題如下：1) 確定回歸函數的類型和估計量，其參數根據實測溫度和應變數據調整；2) 確定溫度和應變之間是否密切相關；3) 回歸誤差與控制[10]。

4.1 應變-溫度的回歸模型

通過對晉蒙黃河大橋箱梁內外溫度及應變數據的分析，發現應變隨溫度的變化上下波動。本節以2018年8月7-8日實地測量數據為依據來做回歸分析。當天山西省河曲縣為陰天，無陽光照射，故箱梁內外溫差較小。經過分析，選擇受陽光影響較小的時段測量出的數據作為參考，即7日晚18:00至8日凌晨6:00的測量數據。將采集系統采樣頻率設置為3 min采集一次，將12個小時分為12個時段，取每個時段所測得的應變值和溫度值數據的平均值，作為當前時段的應變和溫度測試結果代表值。為了更為直觀地看出溫度和應變的關系，下表2為無車輛荷載時，溫度從低到高的順序列出所測數據，都可用來進行回歸分析。

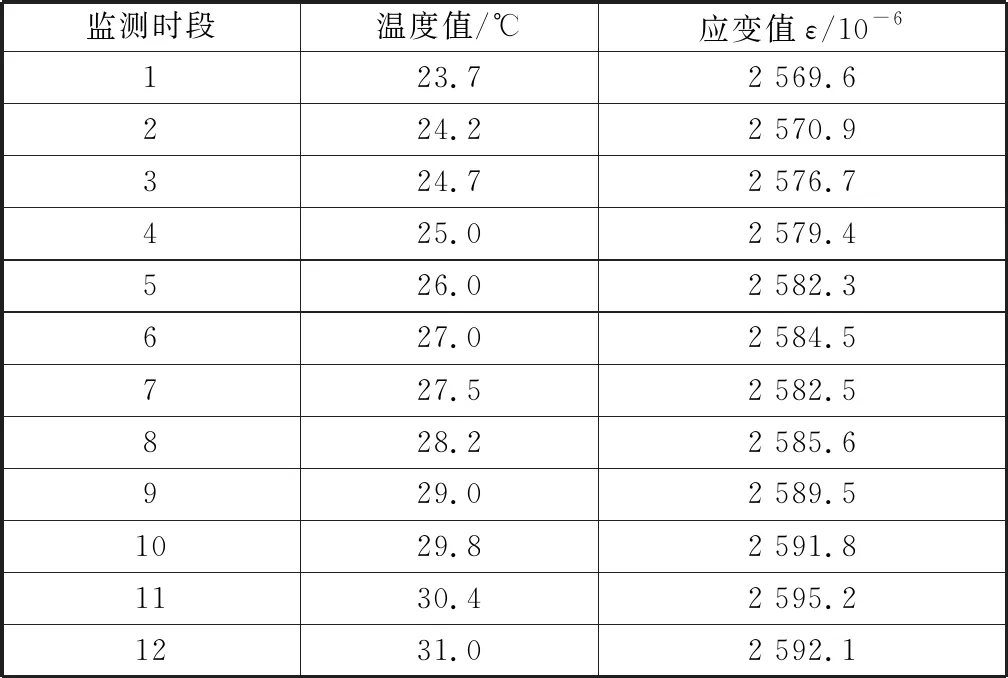
表2 監測斷面的溫度與應變匹配表Table 2 Temperature and strain matchingTable of monitering section

應變和溫度數據散點圖如圖9所示。

由圖9可看出，本系統監測得出的大橋應變與溫度數據之間呈現出大致的線性關系。這樣就可以將應變與溫度之間的關系轉換成線性回歸化模型，而對于變量，則需要假定一個控制變量，將控制變量假定為溫度，最后的回歸函數可寫成[11]：

y=f(x)=β0+β1x.

(6)

一元線性回歸模型為：

(7)

式中：β0，β1稱為回歸系數，β0，β1，σ2均未知；ε在式子中被稱作隨機誤差，服從正態分布。

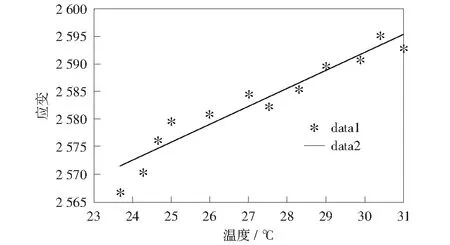
圖9 溫度與應變值關系圖Fig.9 Diagram of temperature and strain

4.2 對參數β0、β1的最小二乘估計

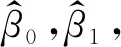
(8)

盡可能小，其中

(9)

叫做yi的預測值。為了讓殘差平方和的結果為最小值，可按最小二乘準則，即使用：

(10)

可得：

(11)

其中：

(12)

經計算可得：

在數理統計中，將

(13)

分別稱為總離差平方和、回歸平方和、殘差平方和。且滿足如下關系：

(14)

4.3 線性回歸顯著性檢驗

從上述內容可以看出，給定一組不相同的數據，例如：(xi,yi)(i=1,2,…,n)，不管是否存在線性相關，都可以求出一個樣本回歸線。明顯地，如果兩者之間不存在線性相關關系，那么尋找回歸線就不存在實際意義。因此，在使用樣本回歸線進行預測和控制之前，有必要檢驗線性回歸關系與樣本回歸線之間的線性關系。

從線性回歸模型中可以看出，|β1|越大，其變化趨勢越顯著；相反，|β1|越小，兩者之間的變化就越不顯著。特別地，當|β1|=0時，意味著無論變化如何，兩者均恒定，不受任何變化的影響，換言之，它與另一個參數之間不存在線性關系。因此，線性回歸的顯著性檢驗歸結為統計假設。

H0:β1=0,H1:β1≠0 .

如果H0被拒絕，則x與y兩者之間存在線性相關，樣本回歸線是有意義的；相反，如果H0被接受，則兩者之間不存在明顯的線性關系，也許兩者存在非線性相關或者無相關性，即使結論如此，也沒有實際意義。本文采用r、t、F等常用檢驗方法來檢驗。

(15)

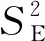
經計算可得，r=0.925 6，在自由度γ=n-2=10，顯著性水平α=0.05下，查詢相關系數臨界值為r0.05=0.522.可得r>r0.05，故拒絕H0，Y與X相關性顯著，即認為溫度X對應變Y有顯著的影響。

根據應變值和溫度值之間的回歸函數，即可對應變進行溫度補償來得到準確的應變數據。

5 結論

1) 本文采用FPGA技術設計了一款基于振弦式應變計的橋梁應變采集系統，可同步并行采集8路應變數據。通過實際的測試表明，本系統測量精度高，滿足工程應用標準。同時解決了工程應用中測量點多、數據量大、采集效率低下的問題。因此，該系統能有效應用于土木工程等領域，前景廣闊。

2) 針對現有測頻方法的不足，本文采用了一種等精度測量法，能實現對頻率變化范圍較大的信號達到同樣的測量精度，而且其測試精度不會受到被測信號頻率大小的影響，誤差在整個頻率區域均保持不變。

3) 本系統依托山西省晉蒙黃河大橋進行實橋實驗，采用時變的平均值法研究在工程應用中溫度對應變的影響。建立應變-溫度回歸模型，最終可對應變值進行溫度補償來得到準確數據。本文所提出的研究方法并不僅適用于應變數據修正，還適用于工程中其他指標的校準，具有較大的應用價值。