基于DEVS的交叉路口建模與仿真①

張學軍,王 寧,王兆鵬

(山西大學 電力工程系,太原 030013)

移動互聯網技術的發展促使城市交通向著智能化的方向發展,在此過程中,需要深入研究交通系統中各因素之間的關系和相互作用.計算機仿真技術作為分析和研究復雜系統問題的有效工具,必定會在智能交通領域發揮不可替代的作用.

交叉路口是現代城市交通的重要組成部分.應用仿真技術,建立交叉路口仿真模型,通過科學分析,實施有效控制,對緩解交通擁堵問題具有積極意義.文獻[1]應用元胞自動機建立了進口道為直左車道和直右車道的交叉路口模型,模型將交叉路口內部分割為若干元胞,各方向車輛通過預先設定的相鄰元胞通過交叉路口,路徑通常是直線或垂直的折線.但路徑的設置對沖突率有較大的影響,可能導致與實際情況不符.此外,文中忽略了右轉車輛和行人之間的沖突;文獻[2]通過增加元胞的數目提高交叉路口模擬的時空分辨率,期望能精確計算車輛行駛速度;文獻[3]提出了一種基于時延的混合Petri 網交叉路口建模方法,模擬了車輛在由交通信號燈控制的雙車道交叉路口的行駛行為,但模型層次結構不夠明顯,計算過程復雜;文獻[4]基于支持向量機(SVM)對交叉路口連通狀態進行了分類,通過轉向關系和轉向次數獲取物理拓撲路網在交叉路口的連通性.但模型的建立需采集大量的浮動車數據,也不能顯式地反映出交叉路口內部的車輛沖突特性.

離散事件系統規范(Discrete Event System Specification,DEVS)是復雜動態系統建模與仿真的一種形式化規范[5],且已被證明與Petri 網、馬爾可夫鏈、元胞自動機等其他離散事件系統模型相比有更強的描述能力[6].使用DEVS 描述交叉路口車輛行駛的動態行為和相互作用更自然靈活.文獻[7]基于DEVS 建立了交叉路口模型,使用“轉向器”作為運輸元件,將待通過交叉路口的車輛看作待轉送的貨物,當出口具備接收條件時將待通過的車輛從進口轉送到出口,但忽略了交叉路口中車輛沖突的復雜性.

本文考慮交叉路口車輛之間、車輛與行人之間的沖突、車輛通過交叉路口時間、路徑和交通信號的作用等要素,在DEVS 框架下建立了描述車輛通過交叉路口動態過程的模型,通過仿真試驗進行了驗證.在余下部分中,第1 部分簡單介紹DEVS 模型的組成和結構,重點介紹并行DEVS;第2 部分建立交叉路口微觀仿真模型并驗證模型的有效性和可靠性;第3 部分提出一種交叉路口智能交通信號控制策略并進行仿真驗證;最后給出本文的結論.

1 DEVS 模型

DEVS 是一種系統建模與仿真的形式化規范,包括原子模型和耦合模型.原子模型是具有獨立構造、內部活動和輸入輸出接口的最基本的元素,它用來描述組成系統的基本實體的動態行為.原子模型相互連接形成耦合模型.耦合模型又可與其它原子或耦合連接形成更大具有模塊化、層次化結構的系統模型.這一特點使得DEVS 特別適合于面向對象建模與仿真.

并行DEVS 與經典DEVS 相比取消了對順序處理的限制,同時將輸入、輸出事件進行打包,使系統能夠并行執行[8,9].并行原子模型定義為一個八元組:

其中,X、Y分別是輸入、輸出事件集;S是狀態集;ta(s)是 時間推進函數,它返回狀態在s(∈S)停留的最長時間;δint(s)是內部轉換函數,描述系統在狀態s的停留時間達到ta(s)后 系統狀態的演化;δext(s,e,x)是外部轉換函數,描述在外部事件x(∈X)的激勵下,系統狀態的演化,0 ≤e≤ta(s)是 在狀態s上已持續的時間;δcon(s,x)是混合轉換函數,描述在內部轉換和外部部轉換同時發生時系統狀態的演化;λ(s)是輸出函數,描述當狀態因內部轉換發生變化時系統產生的輸出,y=λ(s),y∈Y.

2 交叉路口微觀仿真模型

2.1 交叉路口系統分析

圖1 為交叉路口示意圖.WI、EI、NI 和SI 分別為西向東、東向西、北向南和南向北4 個方向的入站路段,EO、WO、SO 和NO 為4 個方向的出站路段.將入站路段分為左轉、直行和右轉3 個車道,到達的車輛按轉向分別進入不同的車道;在交叉路口內畫出不同轉向車輛的行駛軌跡,這些軌跡的交點稱為沖突點.每個沖突點有2 個進入方向和2 個離開方向.車輛在依次通過其行駛軌跡上的沖突點時,如果沖突點處有車輛,則必須等待直至沖突點中的車輛離開.例如:WI-1 車道中的左轉車輛可分別與NI-2 中的直行車輛、SI-1 中的左轉車輛、NI-1 中的左轉車輛及EI-2 中的直行車輛在11、7、5 及3 點發生沖突.交叉口內發生的沖突,增加了交叉口通行的復雜性,成為影響交通通行能力的主要因素.交通控制器(TC)通過燈光信號只允許部分轉向車輛進入交叉口,能有效地減少沖突的次數,提高交通效率,是平面交通控制的主要設施.

2.2 交叉路口的DEVS 建模

車輛通過交叉口的過程可用信息通信系統來比擬,車輛被看作待傳輸的信息.應用DEVS 建模思想,可以建立4 種原子模型來模擬與交叉口通行仿真相關要素及關系,包括:模擬轉向車道的發送器、模擬出站路段的接收器、模擬交通信號的時間信號發生器和模擬沖突點的交換器.

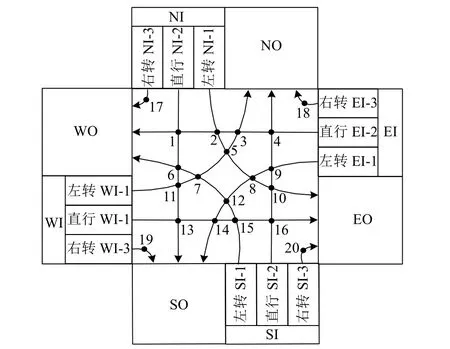
圖1 交叉路口示意圖

轉向車道被建模為信息發送器.當車道內有待通行的車輛時,發送器根據交通信號和連接的沖突點狀態發送車輛信息.發送的車輛是否被成功接收,還取決于發送器是否接收到目標沖突點發送的確認接收信息;出站路段被建模為信息接收器,它無條件地接收沖突點發送來的車輛;交通信號是時間信號發生器,它按給定的綠信比和信號周期輸出紅、綠燈信號;沖突是交叉口通行的主要特征,限于篇幅,本文只詳細介紹沖突點Atomic 模型.

沖突點可用容量為1 的通信交換器來模擬,它的原子模型如圖2 所示.

圖2 沖突點模型

圖2 中,5 個輸入端口組成交換器的輸入端口集:

式中,Recv1和Recv2分別用來接收2 個進入方向發送來的車輛;Perm1和Perm2分別用來接收2 個離開方向發送來的允許/禁止輸出信息;Ackin用來接收2 個離開方向發送的車輛被接收的確認信息.

4 個輸出端口組成交換器的輸出端口集:

式中,Send1和Send2分別用來向2 個離開方向輸出車輛;Load發送允許/禁止向沖突點輸出車輛的信息;Ackout發送車輛被接收的確認信息.

為了描述沖突點交換器的動態行為,首先定義事件集和狀態集.輸入事件集定義為:

輸出事件集定義為:

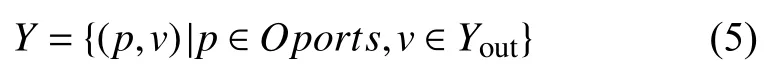
式中,p為事件的端口;v為事件的值;Xin=V和Yout=V分別為輸入和輸出事件的值集,V的元素是車輛序號或布爾量.

沖突點交換器狀態集定義為:

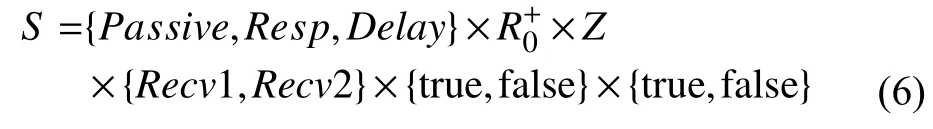
狀態集的元素:

式中,ph∈{Passive,Resp,Delay}為 過程標識,Passive表示交換器內無車輛,等待車輛輸入;Resp表示收到新的輸入,將作出響應;Delay表 示有車輛待輸出;σ ∈是狀態的壽命,即是在無外部事件發生的情況下在狀態s停留的最長時間;v∈Z是待輸出車輛的序號,v=0表示無車輛;port∈{Recv1,Recv2} 是車輛v的輸入端口;sw1 ∈{true,false}和sw2 ∈{true,false}分別表示允許/禁止經端口Send1和Send2輸出車輛.

沖突點交換器外部轉換函數、內部轉換函數和混合轉換函數描述了沖突點交換器的動態行為.分別如下定義,式(8)分5 種情況給出了在外部事件發生時沖突點交換器狀態的變化;式(9)分3 種情況給出了沖突點交換器在狀態壽命自然結束(被稱為內部事件)時狀態的變化;式(10)表當示內外部事件同時發生時,先執行外部事件轉換再執行內部事件轉換;式(11)分5 種情況給出了內部轉換發生前的輸出事件,包括輸出端口和事件值;式(12)表示事件推進函數僅簡單地返回當前狀態的壽命,仿真程序據此確定下一最早事件的發生時間.

式中,x.v和x.port分別為事件x的值和端口.

式中,pass_t為車輛通過沖突點需耗費的時間.

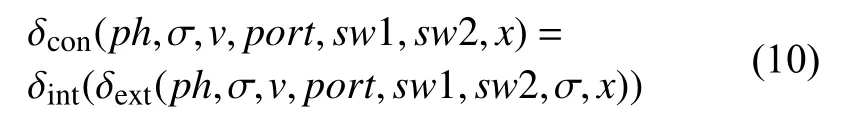
輸出函數和時間推進函數如下定義:

2.3 模型驗證

為了驗證模型,選擇某市城區一典型交叉路口進行觀察統計,用統計數據設置仿真參數,將仿真試驗結果與根據《城市道路設置規范》計算結果進行了比較.

2.3.1 基礎數據調查

該交叉路口包含4 個進口道,每個進口道包含3 條車道,分別為直行、左轉、右轉專用車道,由于交叉路口車輛95%以上為小型汽車,忽略中型和大型車輛.調查結果顯示,車輛到達率服從指數分布.交叉路口相位如圖3 所示,其中,右轉車輛不受信號燈控制,左轉與直行車輛受同一信號燈控制.信號燈周期為125 s,其中第一相位為59 s,第二相位為66 s(含黃燈時間3 s).綠燈亮后第一輛車啟動通過停止線的平均時間為2.0 s,之后車輛通過停止線的平均車頭時距為2.5 s.對同相位兩個方向車輛轉向比例取平均值,兩個相位不同轉向行駛車輛的比例為:第一相位車輛左轉比例為27%,直行比例為52%;第二相位車輛左轉比例為19%,直行比例為65%.車輛直行通過交叉路口的平均時間為6.2 s,左轉通過交叉路口的平均時間為10.38 s,右轉車輛不受交通信號控制,但右轉車輛受行人影響較大,所以對一個周期內右轉車輛通過交叉路口的時間取平均值,約為6.0 s.

圖3 交叉路口相位圖

2.3.2 通行能力計算

《城市道路設計規范》[10]指出,交叉路口的通行能力等于各進口道通行能力之和,各進口道的通行能力等于各車道通行能力之和.本例交叉路口入站車道為左轉、直行和右轉專用,采用以下3 種車道的通行能力計算方法,表1 為各相位各進口道通行能力的計算結果.

表1 各進口道車輛通行能力

1)直行車道的通行能力計算公式:

其中,Cs是 1 條直行車道的通行能力,veh/h;Tc是信號燈周期,s;tg是綠燈時間,s;t0為綠燈亮后,第一輛車輛啟動通過停止線的時間,s;ti為車輛通過停止線的平均車頭時距,s;φ為折減系數,一般為0.9.

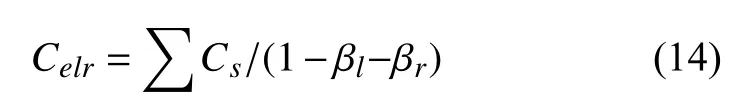
其中,Celr為進口道通行能力之和為本進口道直行車道通行能力之和;βl、 βr分別為左、右轉車占本面進口道車輛的比例.

2)左轉專用車道的通行能力計算公式:

3)由于右轉車不受信號燈控制,右轉專用車道的通行能力為兩個相位車道通行能力之和,計算公式:

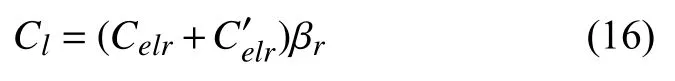
其中,為另一相位進口道通行能力之和.

計算得到交叉路口通行能力為5233.834 veh/h.

2.3.3 通行能力仿真

根據實地統計數據標定模型參數,通行能力仿真結果如圖4 所示.仿真結果顯示,單位時間內通過交叉路口的車流量隨到達率的增加逐漸上升直至穩定,該穩定流量即為交叉路口的通行能力.文獻[10]中根據 《城市道路設計規范》計算得到的設計通行能力比實測結果高10.4%,而本文通過仿真得到交叉路口的通行能力為4620 veh/h,與計算得到的通行能力相對誤差為13.286%,說明交通仿真的結果與實際結果相近,證明模型的可靠性.

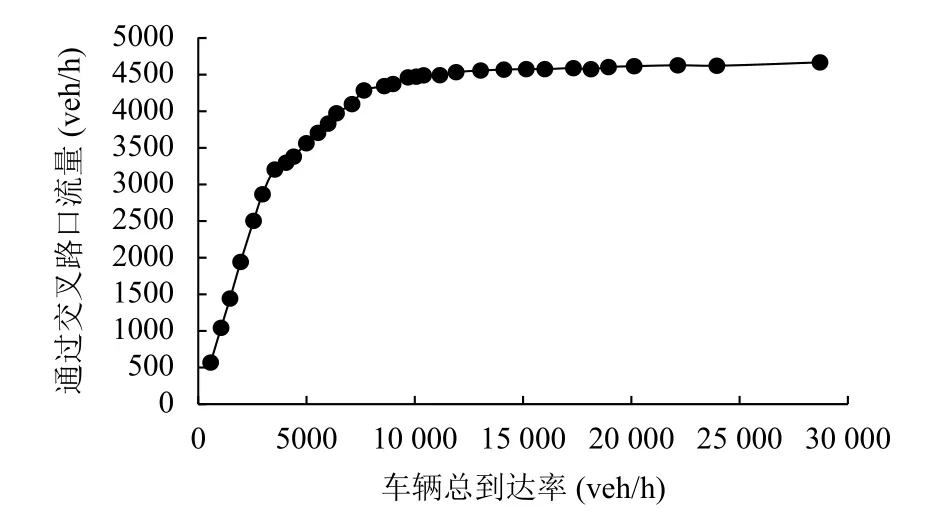
圖4 通過交叉路口流量與車輛總到達率的關系

不同轉向比例直接影響交叉路口的通行能力.假設總車流到達率平均為6000 veh/h(大于通行能力),右轉車輛不受信號燈控制且右轉車比例為0.1.通過增加左轉車輛的比例,同時降低直行車輛的比例,監測左轉比例對交叉路口通行能力的影響,仿真結果如圖5 所示.

交叉路口通行能力先隨著左轉車比例的增加而增大,這是由于左轉與直行同信號,綠燈時可同時通過兩輛車,因此通行能力增加;當左轉比例為0.2 時,交叉路口的通行能力達到最大;繼續增大左轉車比例時,通行能力下降,這是由于各方向左轉車輛與對向直行車輛沖突加強,通過交叉路口的時間比直行車輛要長,從而導致通行能力下降.

圖5 左轉比例對交叉路口通行能力的影響

3 智能交通仿真設計

當前,交通擁堵問題日益嚴重,固定時長的交通控制信號已經不能滿足當前的需求.城市智能交通管控系統[11]作為解決交通擁堵問題的重要手段,能夠提高交叉路口的運行效率,提高行車安全進而推動經濟的發展.文獻[12]根據各相位關鍵車道的流量,采用遺傳算法和自適應遺傳算法優化了車輛平均延誤時間并制定了綠信比;文獻[13]建立了基于門限服務策略的交通信號燈輪詢控制模型,根據交叉路口車輛平均排隊長度,利用馬爾科夫鏈和概率母函數對多個交叉路口進行信號燈時長分配;文獻[14]將東西和南北兩個方向的車流量比值設定為多個狀態,對各種狀態制定了相應的綠信比.這些文獻提及到基于車流量的監測優化信號燈運行系統[15,16]均可以改善交叉路口的通行能力以及減少車輛的延誤時間,但是都不夠精確和實時.本文考慮當一個信號燈周期結束時,通過監測各個路段等待區內等待車輛的數目對下一周期內各信號燈時間進行實時分配,能夠有效減少車輛堆積.通過控制交叉路口信號燈周期不變,將系統各相位的綠信比由兩個相位等待區內最大車輛數的比值作為分配依據,如式(18)所示.

其中,we、ns分別為東西、南北方向等待區內存在的最 大 車 輛 數 目;wl、wt、el、et、nl、nt、sl、st分 別為西向東左轉、西向東直行、東向西左轉、東向西直行、北向南左轉、北向南直行、南向北左轉、南向北直行等待區內車輛數目;Tg1、Tg2分別為東西、南北方向綠燈信號時長;T為交通信號燈周期;η為綠燈最短時長,考慮左轉車通過交叉路口的平均時間為10.38 s,設置η =10.38 s.

為驗證該模型的優越性,假設總車流到達率平均為6800 veh/h(大于通行能力),且同相位下的車輛到達各進口道的比率相同.將該策略與典型的固定時間控制策略進行比較,分析東西和南北兩個方向車輛到達率不同的情況下交叉路口的通行能力,仿真結果如圖6所示.

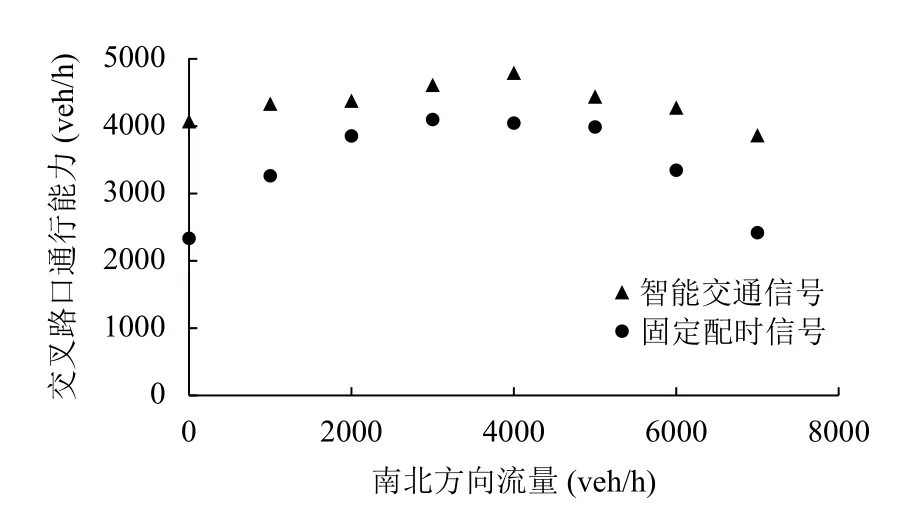
圖6 智能交通與固定配時通行能力對比圖

兩個相位車流到達率差值越大,在智能交通信號下的交叉路口通行能力越優于固定配時信號.交叉路口在南北方向車流到達率為0 的情況下,智能交通下的通行能力比固定配時下的通行能力高74.5%.當兩個方向車流均勻到達時,智能交通下通行能力也比固定配時下通行能力高12.5%,動態調整各信號燈的運行時間,能夠有效解決單車道流量過大的情況,科學疏導交叉路口的車流.

引道延誤時間是指車輛第一次停車到越過停止線的時間,本文基于引道延誤時間分析智能交通信號的優越性.假設東西方向車流到達率大約為4800 veh/h,南北方向車流到達率為1800 veh/h,圖7 所示為28 個周期下每個周期內通過所有車輛的平均引道延誤時間,可以看出,在智能交通信號下平均引道延誤時間均小于固定配時信號.

在智能交通信號的控制下,交叉路口的通行能力顯著提升,車輛的平均等待時間明顯減少.智能交通信號極大地緩解了城市的交通擁堵問題,節約了用戶出行時間并減少了車輛等待期間產生的尾氣污染.

圖7 智能交通與固定配時延誤時間對比圖

4 結論

本研究建立了基于DEVS 的由信號控制和雙向3 車道組成的交叉路口微觀仿真模型.該模型能準確描述交叉路口間車輛的有序以及沖突特性,強化了交叉路口各部分交通狀態并提高了仿真的真實性和準確性.通過仿真得到了車流到達率與交叉路口流量的關系,探究了左轉比例對通行能力的影響,顯示其仿真結果與計算結果誤差為13.286%,驗證了模型可靠;得到了通行能力隨著左轉車的比例的增加先上升后下降的結論,可以看出最優左轉車比例大約為20%.

在此基礎上,改進了受固定配時信號控制的交叉路口,即由路口停止線內等待的車輛數來決定該路口下一周期信號燈的綠信比,進而對信號燈進行智能控制.結果顯示智能交通信號燈極大地增加了交叉路口的通行能力并減少了用戶的平均等待時間.仿真結果表明所建立的基于DEVS 的交叉路口模型具有靈活性且適應性強,可用于其他交通問題的研究.