路面衰減模型中各參數的求解方法解析
楊東濤
(遼寧奧路通科技有限公司,遼寧 沈陽 110006)
對于大部分一線施工人員來說,往往對如何求解模型中各類參數存在諸多疑問,本文將以實例的形式對此問題進行論述解析。
目前,常用的路面性能衰減預測模型有很多種,本文只針對其中兩種給出具體參數求解方法,其他預測模型可參照執行:

已知多年累積數據,已知預測模型公式,如何求出模型中的參數a、b,通過表1給出具體求解方法:
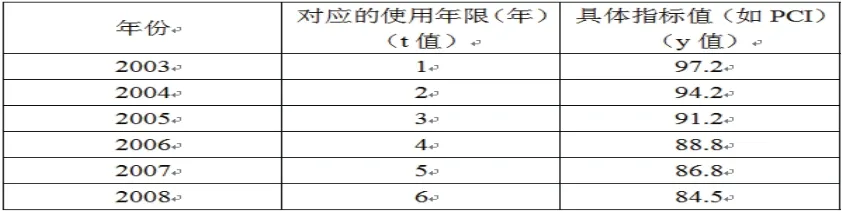
表1 示例所用數據
一、SPSS求解方法
(一)同濟大學模型求解方法
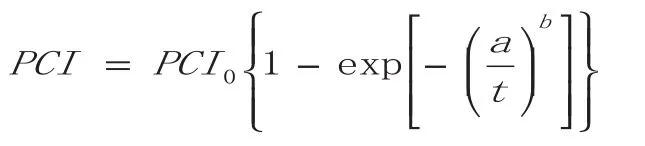
首先,通過“三點法”確定參數a、b初始值,對于本模型,只需先假定一個參數(如b=1),再將t1=1時,y1=97.2,PCI0=100帶入預測模型公式,即可求出b=1時,a=3.575551。
其次,打開SPSS軟件,變量視圖里設置自變量t、因變量y,寬度可設為20列,如圖1所示,數據視圖中根據前面的數據表1,錄入相應的t值和y值,如圖2所示。
圖1 變量視圖
圖2 數據視圖
依次選中SPSS軟件中的“分析—回歸—非線性”,即可打開“非線性回歸”窗口,將y導入因變量中,模型表達式中按照預測模型公式錄入即可,如圖3所示。
點擊“參數(A)”,依次錄入a=3.575551、b=1作為非線性回歸的初始參數,點擊“繼續”,如圖4所示。
在“選項”中選擇“Levenberg-Marquardt(L)”,點擊“繼續”,如圖5所示。
點擊“確定”,即可開始計算,計算結果將在另一個文檔中打開,結果如圖6所示:
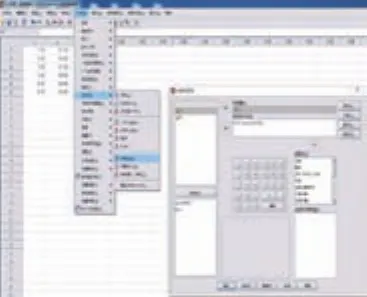
圖3 “非線性回歸”窗口視圖
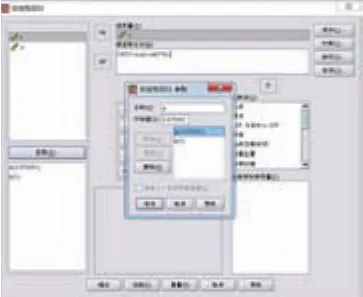
圖4 參數設置視圖
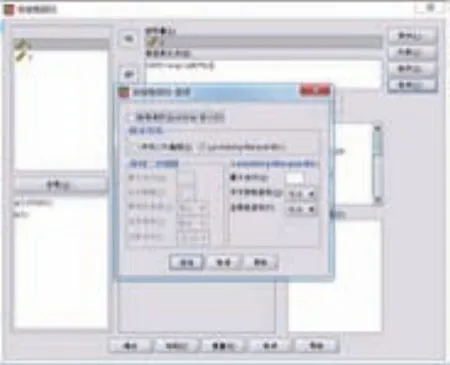
圖5 選項設置視圖
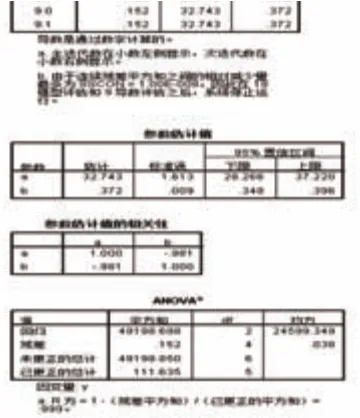
圖6 計算結果視圖
從圖6中可以看出,通過9次非線性迭代計算,結果為a=32.743,b=0.372,R2=0.999。
初始參數a=3.575551、b=1經過非線性計算后,變化為目前的輸出值a=32.743,b=0.372,之所以有這樣的變化,主要原因為初始參數a=3.575551、b=1適用于t1、y1值,不一定適用其后面的tn、yn值,經過重新計算的a=32.743,b=0.372將適用于數據表中的任何tn、yn值。
準確性驗證:SPSS計算結果是否準確需驗證才能證明,方法為將a=32.743,b=0.372帶入預測模型公式中,再將t1至tn的值帶入預測模型公式中,重新計算的y值與前面的數據表1中的y值相同或相近,即可證明SPSS計算結果是正確的,如表2所示。
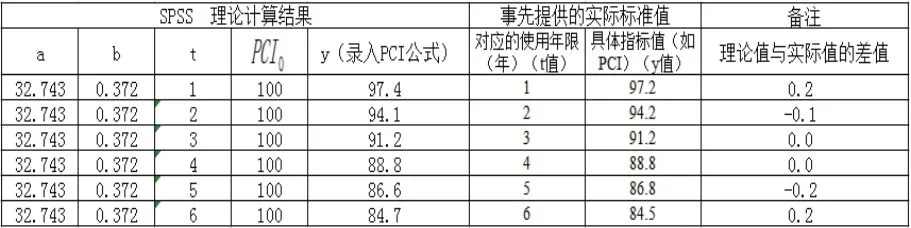
表2 SPSS理論計算值與實際值對比驗證表
通過“理論值與實際值的差值”可以看出,差值很小,且R2=0.999,相關性好,說明SPSS計算結果是正確的。
注:若預測模型公式復雜,參數不止兩個,如有a、b、c三個參數,可采用簡化三點法,即假設其中一個系數為已知值,避免用到三個點去實際求解三個不同系數,難度較大;此時先假設其中一個參數為1(根據公式模型,假設其中一個參數為1,可簡化求解另外兩個參數),再將(t1,y1)、(t2,y2)帶入預測模型公式,求出a、b、c三個參數的初始值即可。
(二)負指數曲線模型求解方法
PCI=a×e-b×t
由于此方程形式簡單,事先不需求解a、b初始值,直接打開SPSS軟件即可,前幾步的設置與圖1、圖2、圖3完全相同。
圖7 選項設置視圖
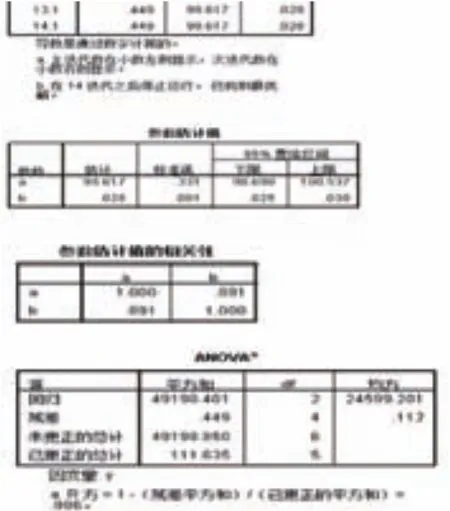
圖8 計算結果視圖
“選項”中選擇“序列二次編程(S)”,點擊“繼續”后如圖7所示。
點擊“確定”,即可開始計算,計算結果將在另一個文檔中打開,計算結果如圖8所示。
由圖8可知,通過14次非線性迭代計算,結果為a=99.617,b=0.028,R2=0.996。
準確性驗證方法同上。
二、Excel求解方法
另外,借助Excel自身的功能,根據已知t值和y值,通過畫散點圖,再添加趨勢線(指數曲線X),顯示公式,即可得到結果如圖9所示。
根據Excel模擬結果,與實際值對比,可發現對于指數趨勢線,其結果與SPSS的負指數曲線基本一樣。但是,針對同濟大學的模型,Excel不能實現,此時才能體現出SPSS的優勢。
三、結論
經過對比驗證,這兩種方法都能較好的模擬出路面衰減情況,且相關性系數均很高(R2均達到0.99以上),但作者更傾向于使用第一種。
1、SPSS求解方法不受模型形式限制,該方法具有較強的通用性,Excel求解方法針對其內部自帶的趨勢線可以很好的模擬,其他形式的Excel不能實現,如同濟大學的模型。
2、同濟大學模型中的a為壽命因子、b為形狀因子,都有具體的含義,理論價值更高,因此推薦使用此模型。
3、負指數曲線模型中的a、b無任何的具體含義,只是這種模型形式簡單,在求解時更容易實現。
4、通過本文的示例解析,可以發現模型中的參數并不是那么難以求解,也無需掌握人工神經網絡、BP神經網絡、遺傳算法、遺傳神經網絡等專家學者推崇的方法才能解決此問題。
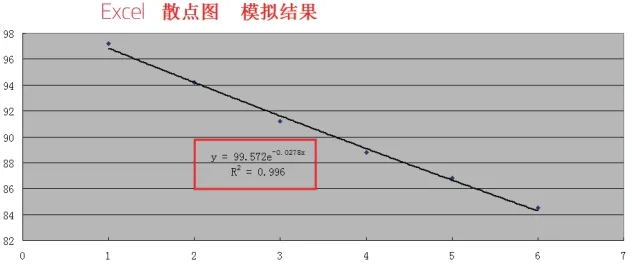
圖9 Excel散點視圖

