基于Petri網的機動車故障診斷專家系統設計*

李永勇，張永進，張燕軍

（1.安徽工業大學 數理科學與工程學院，安徽 馬鞍山 243032；2.揚州大學 機械工程學院，江蘇 揚州 225127）

0 引言

隨著道路交通的快速發展，機動車已成為人們日常工作生活中不可或缺的一部分，因此機動車的可靠性、故障維修以及如何快速有效地診斷出機動車的故障源越來越受到人們重視。傳統的機動車故障診斷過程復雜、效率低且對維修人員的素質要求較高，因此設計一種能夠快速診斷故障并能給出維修方案的專家系統具有重要的現實意義。

當前，已研究的機動車故障診斷專家系統模型主要有基于知識的［1］、規則的［2］、實例的［3］及其組合的［4］，以及基于模糊邏輯的［5］和人工神經網絡的［6］等。雖然傳統的專家系統不需要精確的分析模型，但因缺乏知識自學習，難以獲取知識和建立知識庫，從而不能滿足當前需求。FTA（故障樹分析）雖然簡單可靠，但傳統的面向割集的FTA需要精確的分析模型和故障機理分析，且該方法計算復雜度高，不易用計算機實現。

為了避免上述診斷方法的缺陷，本文在FTA的基礎上，設計一種基于Petri網求最小割集的機動車故障診斷專家系統。該系統采用結構模塊化設計，利用知識庫中的知識設計故障推理機，實現對機動車故障的快速定位并給出故障維修方案，且可利用自學習功能對專家知識庫進行更新擴充。

1 故障診斷專家系統結構設計

1.1 Petri網基本模型

故障樹是系統故障發生和傳播的邏輯表示，它通過特定的事件、邏輯門和其他符號來描述系統中事件的因果關系。

由故障樹底部的事件狀態xi完全確定頂部事件狀態Φ，xi只有1和0兩種狀態，故障樹結構函數為Φ＝Φ（x1，x2，…，xn）。對于大型復雜系統的故障樹，采用下行法或上行法求解最小割集時將會顯得十分繁瑣，相比之下，Petri網是一種較為簡潔有效的方法。Petri網是一種由節點和定向弧長組成的二元有向圖，將故障樹中的事件轉換為Petri網中的庫p，用圓圈表示，并將邏輯符號轉換為變遷t，通過直線段或矩形表示，可直觀地體現出故障的動態傳輸過程。

在Petri網中，若從庫所p到轉移t的輸入函數是非負整數w，則標記I（p，t）＝w，用p到t的有向弧和旁注w表示；若從轉移t到庫所p的輸出函數是非負整數v，則標記為O（p，t）＝v，用t到p的有向弧和旁注v表示。I和O是n·m非負整數矩陣。關聯矩陣A是O 和I 之 間 的 差，即 A＝O－I［7－8］。根 據 文獻［9］，可將故障樹轉化為Petri網，如圖1所示。

圖1 故障樹邏輯門的Petri網表示

1.2 專家系統結構設計

機動車故障診斷專家系統主要由人機交互界面、故障特征信息庫、專家知識庫、推理機、解釋機五部分組成，其結構框圖如圖2所示。

圖2 機動車故障診斷專家系統結構框圖

用戶通過人機界面提供相應故障特征信息，系統利用專家知識庫中存儲的知識，按照相應的推理策略進行逐級匹配診斷后，由人機界面顯示出推理結果。因為不同用戶對機動車故障的描述會因其所掌握相關專業知識程度的不同而不同，所以需要對故障描述內容進行特征提取并統一表示，組成故障特征信息庫。系統將機動車故障特征信息和專家知識等導入知識庫中進行數據庫操作，包括增刪改等，即為知識獲取過程，如圖3所示。

圖3 知識獲取過程框圖

專家知識庫由故障樹和規則庫兩部分組成。故障字典的形成過程也是故障樹的建立過程，如果故障的原因不在知識庫中，則會在故障字典中填寫，并繼續擴展知識庫。規則庫是專家知識通過“生產表示”來表達的，符合人的思維習慣，可以清晰表達專家知識，如最小割集為｛X1，X2｝，那么產生式表示為IF X1AND X2THEN R1，其中R1表示相應導致的故障。

在整個專家系統的診斷過程中，解釋機將推理機推理出的故障診斷結果和維修方案展示給用戶。作為系統核心部分的推理機可從規則庫中推斷出故障模式，其過程是用“產生式規則”來表示，并按規則進行查找相關故障樹的割集，這些割集與知識庫中的規則是一一對應的。故障診斷推理的具體流程見圖4。

2 機動車故障的最小割集排序

2.1 機動車故障樹模型

常見的機動車故障主要由電控汽油噴射發動機常見故障、傳動系常見故障、制動系常見故障和車身常見故障等故障分類組成。如果對傳動系常見故障再進行細分的話，主要有離合器故障、手動變速器故障和自動變速器故障等。對上述故障部件進行故障樹分析，可得相應由若干種故障的原因為底事件組成的子故障樹，即為元件故障樹。而基于元件故障樹的系統數據庫中的數據也就成為機動車故障診斷的依據。元件故障樹的每個割集為一種故障模式，且與專家知識庫中的規則相對應。

機動車故障樹如圖5所示，將機動車故障作為頂事件，常見的七類機動車故障作為第二層子節點，再下層為機動車七類故障對應的子故障樹，此處以離合器故障為例，X1至X11為離合器故障的底事件。

圖4 故障診斷推理流程

圖5 機動車故障樹

2.2 基于Petri網的最小割集排序方法

為了便捷地求出機動車故障樹的所有最小割集，系統利用Petri網關聯矩陣求最小割集。矩陣中，1表示由變遷指向庫所的有向弧，－1表示由庫所指向變遷的有向弧，0表示變遷與庫所間無指向關系。可將故障診斷推理的過程有效地轉化為矩陣數學運算求出最小割集［10］，過程如下：

（1）在關聯矩陣中，找只含有“0”和“1”的行對應為頂庫所，按此行中的“1”列查找“－1”，此“－1”行表示的庫是頂庫的輸入庫，如果列包含多個“－1”，則意味著有多個輸入庫對應于同一轉換，且為“與”的關系。

（2）根據步驟（1）中的“－1”行，尋找“1”，如果“1”指示庫是中間庫，繼續通過步驟（1）循環查找“－1”，直到該行上沒有“1”。若沒有“1”，則表示為基庫所。若該行中有多個“1”，則這些“1”所對應的庫所之間是“或”關系。

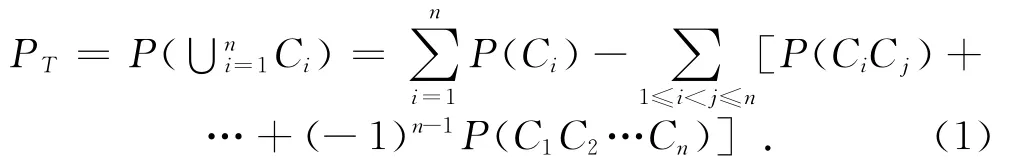
（3）按步驟（1）和步驟（2）繼續尋找，直到找到底庫所為止。

（4）將底庫所展開，根據布爾吸收律或質數法求出所有最小割集。

通過上述求最小割集過程可以看到，利用Petri網關聯矩陣法可快速有效地求出故障樹的最小割集，算法清晰，并且易于計算機實現。

機動車故障分析所建立起來的故障樹十分龐大，如果在機動車發生故障后對每個最小割集的底事件進行依次檢查，不僅工作量大，而且效率低下甚至不可行。因此在計算底事件概率的基礎上進行最小割集的重要度分析，計算并排序每個最小割集的重要度，值越大的優先級越高，反之亦然。最小割集重要度是指它相對于頂事件發生的概率，而頂事件概率可以由底事件的故障概率來求解。

例如通過上述過程求出機動車故障樹的n個最小割集Ci（i＝1，2，…，n），可計算頂事件發生概率PT：

其中：P（C

i

C

j

）（1≤i＜j≤n）為兩個割集同時發生的概率（即兩個最小割集發生概率之積）；P（C

1

C

2

…C

n

）為n個最小割集同時發生的概率（n個最小割集發生概率之積）。

當最小割集可靠度較大時，頂事件發生概率收斂很快，可將頂事件發生概率PT近似解為PT≈，求出所有最小割集的重要度Ii為：

再根據Ii的大小來排序制定診斷優先級，并以此來快速診斷出機動車故障原因，從而降低診斷系統分析的難度和工作量，提高一次診斷故障原因的可靠性。最后，利用專家系統故障分析可找出機動車制造設計薄弱環節并計算出可靠度Rs＝1－PT［11］。通 過 對 薄弱環節采取相對應的措施，如對易發生故障的部件進行改造升級，從而可減少故障的發生。

3 實例分析

由于機動車故障樹較為復雜，所以本文只對某型機動車的離合器故障底事件進行故障樹分析，表1給出了該機動車離合器故障樹底事件。

表1 某型機動車離合器的故障樹底事件

為了便于故障樹轉化Petri網，該離合器故障樹只涉及了AND門和OR門，用多輸入變遷代替AND門，用兩個變遷代替OR門。圖6和圖7分別給出了離合器故障樹和相應的Petri網。

圖6 機動車離合器故障樹

圖7 離合器故障樹對應的Petri網

由圖6和圖7可知，故障樹的底事件與Petri網的庫所的對應關系，如表2所示。

表2 故障樹底事件與Petri網庫所的對應關系

可以得出Petri網對應的關聯矩陣A＝O－I，具體如式（3）所示：

根據式（3）關聯矩陣求故障樹最小割集：

（1）搜索只有“1”和“0”沒有“－1”的行，此例中為第16行，得到：

p16＝p15＋p14＋p13＋p12.

（2）對行15、14、13、12分別找為1的列，重復上述步驟，得到：

（3）將所有底庫所求出后，將以上算式逐級代入，并整理后得：

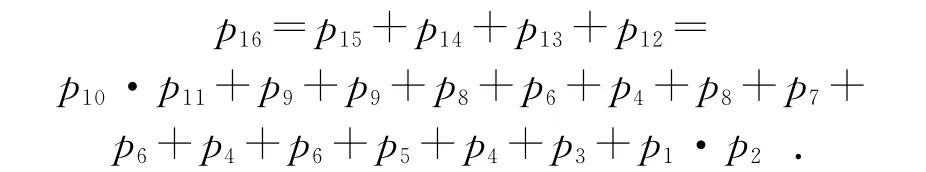
（4）最后按照布爾吸收律或素數法得出離合器故障樹的最小割集，最小割集與底事件的對應關系如表3所示。

由專家經驗可得到某型機動車離合器各底事件概率，見表4。

表4 機動車某型號離合器底事件發生概率

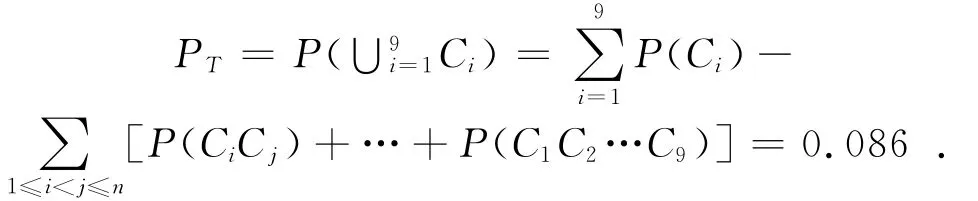
用式（1）求離合器故障頂事件發生概率為：對所有最小割集進行式（2）中的重要度Ii計算，得到的最小割集重要度見表5。

表5 最小割集的重要度

根據最小割集Ii的大小確定優先級：

然后根據所求優先級排序對機動車離合器進行故障診斷，優先級高的底事件的發生更易導致故障發生，因此，在進行故障診斷維修時優先考慮會有更好的效果。

根據定性分析可知，C2、C4為機動車離合器發生故障的主要原因，對C2、C4中的底事件X3、X5中部件進行改進，降低其故障的發生概率為X3＝0.005，X5＝0.002，可計算出改造升級后的離合器故障發生率PT′＝0.057和可靠度Rs＝0.943。故障部件經過改造后，提高了機動車離合器的可靠性。

4 結論

針對傳統的面向割集的故障樹和專家系統的不足，提出并分析了基于Petri網的機動車故障診斷專家系統。

（1）該系統綜合利用各種類型的故障特征，整合多渠道故障診斷信息，使診斷結果更加精確可靠，彌補了傳統方法的很多不足，可快速精確地診斷典型故障并給出可行的解決方案。

（2）該系統的診斷推理引擎利用知識庫中的知識進行推理，并利用故障樹對應的Petri網快速地求出最小割集，實現對每個底事件重要性的分析，極大地簡化了FTA的計算。

最后通過實例，對機動車離合器的故障診斷進行分析，并對其故障部件進行維修改善后，使得離合器的可靠性有所提高，證明了設計的故障診斷專家系統的實用性。