基于橋式起重機橋架裂紋有限元應力分析

趙志強，邱常明，蔡玉強

（華北理工大學 機械工程學院，河北 唐山 063210）

0 引言

起重機由于長期處于高負重的工作循環條件下，致使橋架主梁處經常出現裂紋，目前，對于此類問題基本都是在裂紋產生的部位進行補焊來修復裂紋，缺乏理論依據和仿真分析［1］。現階段，我國起重設備的設計依然主要基于經典力學理論對主梁、端梁等主要受力部位進行分析。浙江大學邢麗靜［2］以橋式起重機主梁為研究對象，對其進行結構分析與優化，并成功開發了“雙小車橋式起重機主梁結構分析與優化設計平臺”；李志雄等［3］采用改進的人工蜂群算法對主梁進行結構優化設計。一般設計人員對橋架的設計現大多采用許用應力法，通過計算橋架的靜強度來校核橋架的整體穩定性，即計算各個部位的應力大小不應超過該材料的許用應力，尤其是要考慮設備處于極端狀態的情況，通常采用應力比法、無限壽命設計法等［4］。

針對某廠橋式起重機橋架部位斷裂問題，本文建立了相應的起重機模型，并基于SolidWorks有限元軟件對其相應部位進行應力分析，分析出應力集中區域，從而進一步分析其產生裂紋的主要原因，并提出相應的解決措施。

1 橋架裂紋理論分析

材料或構件在交變載荷的作用下會產生與靜載荷作用下不同的力學行為，在反復的交變載荷的連續作用下［5］會在其最大載荷遠低于靜載荷的破壞極限載荷下產生疲勞損傷或疲勞斷裂的現象。由于長期處于不斷受到交變應力［6］的作用環境，材料以及各項性能的下降導致了裂紋的產生，一旦裂紋出現，就要考慮到裂紋的擴展。

1.1 裂紋的受力和斷裂特征分類

為了理論研究方便，線彈性斷裂力學將實際構件存在的缺陷簡化為平面裂紋或反平面裂紋問題處理。根據不一樣的外加作用力與斷裂特征，將裂紋劃分為三種類型，如圖1所示。

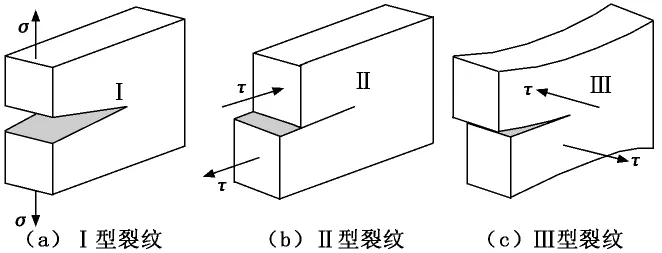
圖1 按裂紋受力與斷裂特征分類

（1）Ⅰ型裂紋（張開型）：這種裂紋的特征是外加拉應力σ垂直于裂紋面，也垂直于裂紋擴展的前沿線，在這種外力的作用下，裂紋沿原裂紋開裂方向延伸［7］。

（2）Ⅱ型裂紋（滑開型）：這種裂紋的特征是外加剪應力τ與裂紋面平行，但是垂直于裂紋擴展的前沿線［8］，在這種外力的作用下，裂紋擴展會偏離擬開裂方向，并與其成一定角度。

（3）Ⅲ型裂紋（撕開型）：這種裂紋的特征是外加剪應力τ與裂紋面平行，也同裂紋擴展的前沿線平行，造成裂紋面錯開［9］，在這種外力的作用下，裂紋通常沿原開裂方向延伸。Ⅲ型裂紋分析較為簡單，又稱為反平面問題［10］。

（4）復合型：實際上，有時候拉應力與剪應力同時存在，可能會出現Ⅰ型＋Ⅱ型、Ⅰ型＋Ⅲ型、Ⅰ型＋Ⅱ型＋Ⅲ型等情況。

理論分析和經驗都證明：在研究復合型裂紋時，從構件安全和處理方便的角度出發，通常將其簡化為Ⅰ型裂紋，Ⅰ型裂紋是受力狀態最為危險的裂紋，因而也成為研究的主要類型。

1.2 斷裂力學K準則

在斷裂力學中存在一種K準則用來表示平面應變斷裂的情況，其具體內容如下：對于載荷作用下的含裂紋物體，應力強度因子是表征裂尖應力強度大小的獨立參量［11］，它是通過確定裂尖周邊的應力場來判斷裂紋或缺陷是否會擴展與長大，進而造成構件破壞的依據。因為在實際工況中，大多數構件的破壞是被拉開的，因此Ⅰ型裂紋最常見也最危險，應著重對Ⅰ型裂紋進行分析。物體對裂紋擴展都具有一定的抵抗能力，只有K值達到或超過其臨界值KC（KC通常稱為平面應力的斷裂韌度）時裂紋才會失穩擴展，發生斷裂［12］。因此以Ⅰ型裂紋為例，發生斷裂（或裂紋擴展）的臨界條件是KI＞KIC。KIC是含裂紋物體材料抵抗宏觀斷裂（或裂紋擴展）的韌度參數，故稱為斷裂韌度，是材料本身的物理特性，表明其在斷裂前吸取能量的能力［13］，是斷裂韌性表征材料阻止裂紋擴展的能力，是度量材料韌性好壞的一個定量指標。在加載速度和溫度一定的條件下，對某種材料而言KIC是一個常數，它與裂紋本身的大小、形狀及外加應力大小無關，是材料固有的特性，只與材料本身、熱處理及加工工藝有關（因此常通過試驗測得，如 Q235B的KIC值為235 MPa）。當裂紋尺寸一定時，材料的斷裂韌性值越大，其裂紋失穩擴展所需的臨界應力就越大；當給定外力時，若材料的斷裂韌性值越高，其裂紋達到失穩擴展時的臨界尺寸就越大，因此它是應力強度因子的臨界值。

強度因子KI的計算公式為：

其中：σ為所受應力；Y為與裂紋形狀、加載方式有關的形狀修正系數，一般規則形狀下取Y＝1.12；α為裂紋長度因子，通常取α＝0.5。

對于穩定性分析，采用穩定性系數n＝KIC／KI。n值界定為1，數值越大表明構件越穩定，反之易發生斷裂，因此當KI≥KIC時裂紋會失穩擴展。由式（1）可知，當出現一定裂紋時，KI值取決于應力σ，為避免裂紋的進一步失穩擴展應分析出應力集中區域，盡量減小應力。

2 橋式起重機橋架主梁有限元分析

針對某廠橋式起重機橋架部位斷裂問題，本文基于SolidWorks軟件進行建模，并通過SolidWorks Simulation有限元軟件對橋架主梁進行應力分析。

2.1 建立有限元模型

建立的起重機橋架主梁三維模型如圖2所示。金屬橋架為正軌箱型的雙梁結構，主要結構由兩根主梁、兩根端梁連接而成，主梁上下蓋板與腹板均用角焊縫相互拼接，主梁內部主要包括大隔板、小隔板、加筋板等。主梁與端梁用連接板焊接，端梁之間用抗剪螺栓緊固聯接，從而使橋架構成一個整體的金屬箱型框架結構。

主梁選用Q235B的普通碳鋼，其抗拉強度為370 MPa～500MPa，彈性模量為210GPa，屈服強度≥235MPa［14］。進行有限元分析時，首先進行網格劃分，本模型采用混合曲率的網格類型，雅克比點為4，最大單元為735mm，最小單元為147mm，網格品質為高，網格劃分完畢后共有70 031個節點、34 518個單元。橋架主梁有限元模型如圖3所示。

圖2 起重機橋架主梁三維模型

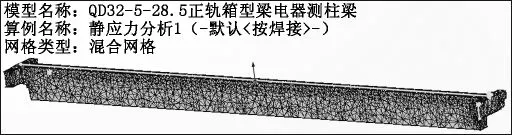
圖3 橋架主梁有限元模型

2.2 載荷分析

（1）自重載荷：包括主梁橋架、小車金屬結構等這些對計算結果影響較大的部件自重。主梁橋架自重G梁＝15.3t，小車金屬結構自重G車＝1.102 4t。

（2）所吊物品載荷：本文取起重機最大的吊運重量，即額定起重量G物＝32t。

（3）垂直動載荷：起重機在吊運過程中，需要經常起升、制動，根據動能原理，需要有額外的力來抵抗這種變化，所以還需承受由于速度變化產生沿其加速度反方向的沖擊力。垂直動載荷包括小車和吊物所受沖擊載荷，根據有關資料可知，小車和吊物所受沖擊載荷分別為：

其中：φ1、φ2為載荷系數，取極限值φ1＝1.1、φ2＝1.08。

（4）水平動載荷：起重機在水平方向上運行，開始啟動或突然制動時產生了水平動載荷Ph，其通過小車車輪作用在橋架上。水平動載荷Ph計算公式為：

其中：a為起重機啟動或制動時的加速度，a＝0.22m／s2；φ3為水平動載荷系數，1≤φ3≤2，取中值φ3＝1.5。

2.3 有限元分析結果

由于起重機及其附屬部件的自重載荷基本是不變的，吊運載荷是經常變化的，致使橋架主梁承載載荷不同，受力部位有所差異，因此主要根據小車在跨中和左端極限位置以及不同負載劃分為不同工況，并根據實際情況對載荷進行組合分析，見表1。不同工況下分析得到的主梁應力和位移云圖如圖4～圖7所示。

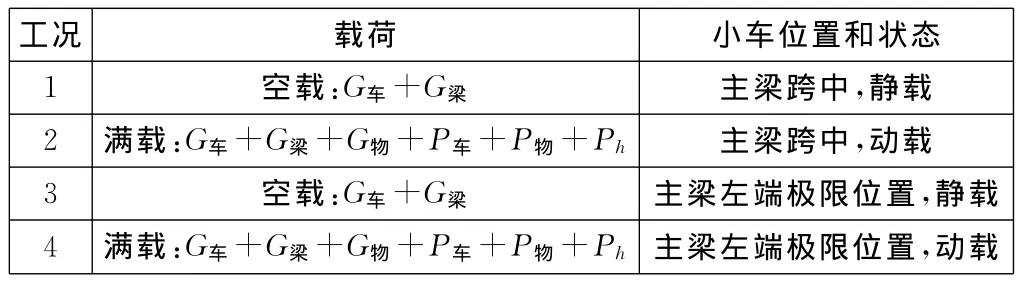
表1 各工況及載荷

由圖4～圖7可知，最大位移發生在主梁中部，最大應力位于主梁彎角處，工況1～工況4對應的最大應力分別近似為 49MPa、128MPa、53MPa、198 MPa，最惡劣的工況為工況4。工況4下的主梁彎角處應力云圖如圖8所示。

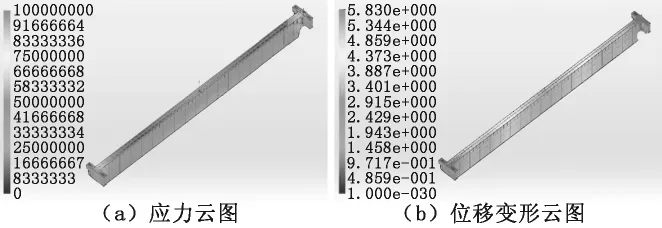
圖4 工況1下的主梁應力和位移變形云圖

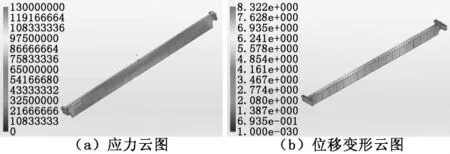
圖5 工況2下的主梁應力和位移變形云圖

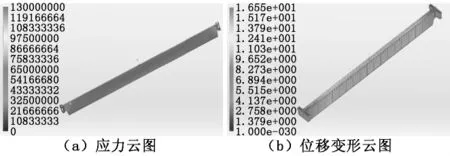
圖6 工況3下的主梁應力和位移變形云圖

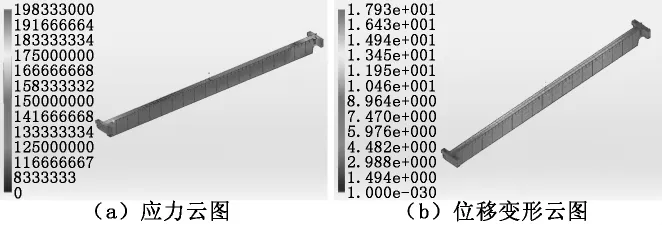
圖7 工況4下的主梁應力和位移變形云圖

圖8 主梁彎角處應力云圖

由式（1）計算得到的各工況KI值如下：

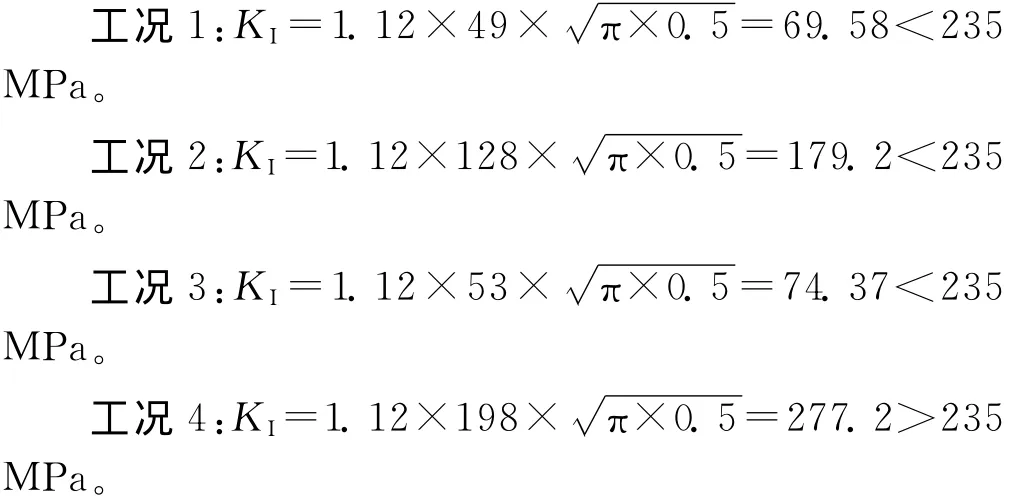
通過上述計算可知：工況4下KI＞KIC，在主梁彎角處會出現裂紋，這與主梁實際斷裂處情況（如圖9所示）相吻合，說明上述有限元分析正確。

3 裂紋修復

通過對上述應力集中區域的分析，提出了對橋架處裂紋的修復方法。在裂紋產生處的兩側安裝補強板，為減少應力集中，且滿足補強板尺寸時至少覆蓋圖8顯示的應力集中區域，保證與原鋼板貼合嚴密后焊接，板上開塞焊孔塞焊，塞焊孔間距為150mm均勻布置，孔直徑取Φ35mm，補強板與腹板厚度一致取8mm，材料為Q235B，如圖10所示。將補強板添加到之前的模型中重新進行應力仿真分析，得出的結果如圖11所示。修復后的應力值比修復前下降了70%，且應力集中區域消失，證明該方法合理有效。

圖9 主梁裂紋實物

圖10 補強板尺寸

圖11 修復后主梁彎角處應力云圖

4 結語

本文對橋式起重機橋架結構進行三維建模，基于有限元應力分析得到主梁的應力云圖，分析出對應的應力集中區域在主梁的腹板彎角處，明確了橋架處產生裂紋的起因。通過在應力集中區域安裝補強板的措施來減少應力，修復后的應力值比修復前下降了70%，且應力集中區域消失，說明本文提出的方法有效。