基于卡爾曼濾波器的索道轎廂相對定位方法及應用

蒙 娟，丁洪濤

（1.北京勞動保障職業學院，北京 100029；2.深圳前海索士科技有限公司，廣東 深圳 518052）

0 引言

客運索道是一種現代化的立體軌道交通設施，由于它安全、快捷、高效、環保，目前在我國風景區和滑雪場得到了廣泛應用。隨著經濟的發展，人們對乘坐索道的安全性和舒適性有了更高的要求。其中，索道轎廂的實時精準定位是實現索道運營安全、乘坐舒適的必要前提。通過對索道轎廂的實時定位，人們能隨時掌握轎廂的精確位置，以便發生危險時進行緊急救援；通過對索道轎廂的實時定位，索道實現定位播放音視頻，旅客可以乘坐索道走到哪聽到哪，旅行途中不再單調，乘坐體驗感更好。因此，客運索道定位系統的研發受到索道行業的普遍關注。

而客運索道多是建造在奇山異水、崇山峻嶺之處，地理環境復雜惡劣，衛星信號容易受到森林、高山的遮擋，出現信號不連續、不穩定，定位精度不高等現象，造成索道轎廂位置定位不夠精準，同時，索道轎廂運行速度慢，且轎廂之間間距較小，加大了轎廂定位精準的難度。本文提出一種基于卡爾曼濾波器的GPS相對定位新算法用于解決這些問題。

1 索道轎廂相對定位原理

1.1 基于GPS的索道轎廂相對定位

GPS是一種無線電導航定位系統，它利用導航衛星進行測時和測距，確定用戶在空間特定坐標系中的位置。GPS定位分為單點定位和相對定位。GPS相對定位也叫差分定位，是目前GPS測量中定位精度最高的定位方法，它被廣泛應用于大地測量、精密工程測量、地球動力學的研究及精密導航中［1］。

索道轎廂相對定位就是設置一個固定位置即坐標精確已知的基站（通常為索道站房），通過測定索道每個轎廂與基站之間的Δx、Δy、Δz坐標分量，從而計算出每個轎廂的精確坐標。同時，根據轎廂相對定位隨時間的變化，結合索道線路的基本方位和走向信息，分別計算出索道多個轎廂的運行方向，為索道控制系統提供精確的轎廂定位信息［2］。索道系統包含轎廂和站房，適合采用差分定位技術進行索道轎廂的相對定位。

1.2 索道轎廂位移測量方法

索道轎廂相對定位的輸出結果是經緯度，而數據處理時需要的是索道轎廂實際位移，因此需要將經緯度換算成位移。把半徑為R的地球置于直角坐標系中，球心位于坐標原點，赤道L所在平面與坐標X、Y構成的平面重合，將經緯度換算成位移示意圖如圖1所示。（注：地球實際為橢球體，長半徑為6 378 137.07 m，短半徑為6 356 752.48m［3］，若將地球看成球體，誤差為千分之三，對項目影響非常小，因此本文將地球看成球體進行計算。）

圖1 將經緯度換算成位移示意圖

地球表面有一點P，坐標為（x，y，z），設α、β分別是經度和緯度，顯然有：

若P點移動一段位移ds，則：

對式（5）～式（7）求平方得：

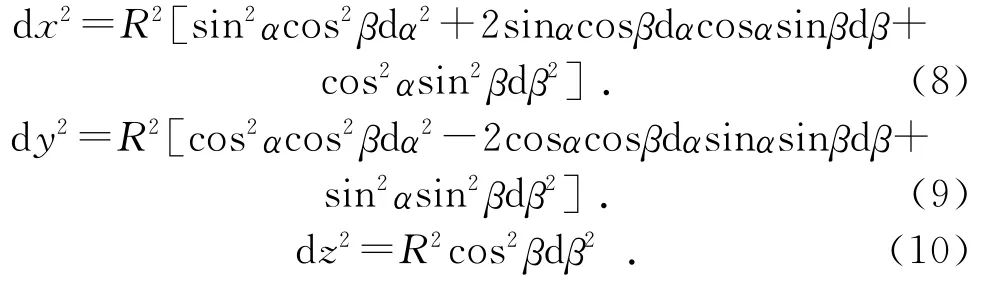
將式（8）～式（10）代入式（4）得：

可見位移ds被分解成沿東西方向的分量Rcosβdα和沿南北方向的分量Rdβ。

2 基于卡爾曼濾波器的索道轎廂相對定位

卡爾曼濾波是一種利用線性系統狀態方程，通過系統輸入輸出觀測數據，對系統狀態進行最優估計的算法。由于它便于計算機編程實現，并能夠對現場采集的數據進行實時的更新和處理，因此，卡爾曼濾波在通信、導航、制導與控制等多領域得到了廣泛的應用［4］。卡爾曼濾波器要求建立數學模型來描述系統，所建立的數學模型與系統的真實模型越匹配，則濾波器輸出的最優估計值越接近于真實值。

為了方便乘客上下，使乘客獲得更好的乘坐體驗感，一般客運索道的行駛速度不會太高且運行平穩，大多數索道站內速度不高于1m／s，站外速度不高于10 m／s。而GPS采樣周期很短，因此我們可以將索道轎廂的運動看作是勻速運動，并以此來建立數學模型。

首先我們要利用系統的過程模型，來預測下一狀態的系統。設轎廂與站房之間的距離狀態量為S，建立的狀態方程如下：

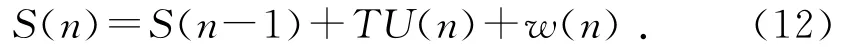
其中：S（n）為在n時刻索道轎廂與站房之間的距離；T為采樣周期；U（n）為系統激勵輸入向量；w（n）～N（0，Q）為過程噪聲。

設轎廂與站房之間的距離實際測量值為Zg，建立的觀測方程如下：

其中：Zg（n）為在n時刻的系統測量結果，由1.2中通過GPS定位采集的計算式（11）導出；H（n）為測量系統參數，此處 H（n）＝I，I為單位矩陣；v（n）～N（0，R1）為測量噪聲。

根據上述的狀態方程和觀測方程建立卡爾曼濾波器。

2.1 預測

（1）預測值。設S（n｜n－1）為卡爾曼濾波器在n時刻的預測值，則：

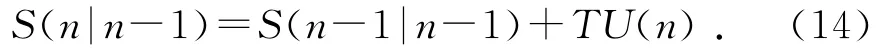
其中：S（n－1｜n－1）為n－1時刻系統的最終優化狀態值。系統激勵輸入向量U（n）推導過程如公式（15）所示：

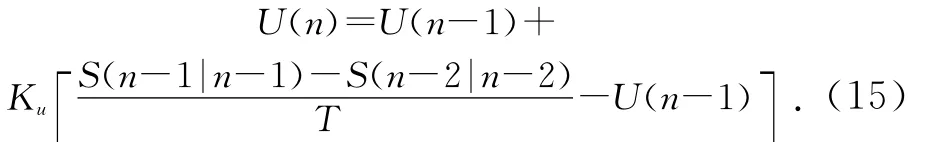
其中：Ku為U（n）的卡爾曼誤差增益。

（2）預測方差矩陣。設P（n｜n－1）為系統預測方差，則：

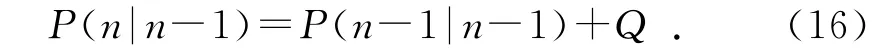
其中：P（n－1｜n－1）為上一時刻的系統修正方差；Q為過程噪聲高斯分布尺度參數。

2.2 修正

（1）誤差增益。設Ks為S（n）的卡爾曼誤差增益，則：

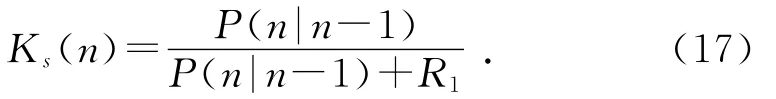
其中：R為測量噪聲高斯分布尺度參數。

（2）修正值。設S（n｜n）為系統在n時刻的最終優化狀態值，也就是卡爾曼濾波器的系統輸出值，即濾波結果，則有：

S（n｜n）＝S（n｜n－1）＋Ks（n）［Zg（n）－S（n｜n－1）］.（18）

（3）測量值。測量值Zg（n）的值由索道轎廂的位移測量方法得出，詳見1.2中公式（11）的推導，即：

（4）修正方差矩陣。設P（n｜n）為系統修正方差，則：

至此，已經完成整個系統的遞推計算。卡爾曼濾波器的輸入為GPS定位模塊采集的經緯度，即α、β，通過對其進行轉換可得索道轎廂相對索道站房的實測距離，經過上述遞推演算，最終獲得系統濾波結果S（n｜n）。

3 實驗結果及分析

采用本文所研究的基于卡爾曼濾波器的索道轎廂相對定位方法，對深圳市東部華僑城景區索道開展實驗。由于天氣、環境、索道運行速度等因素都會對轎廂位置的測量造成影響，因此通過設置特定濾波系數、修正值和不確定系數后，獲取索道轎廂位置在濾波前、后的試驗結果，如表1所示。表1中，濾波前的值為測量值，即Zg（n），濾波后的值為濾波器輸出值，即S（n｜n）。

濾波前、后的索道轎廂時間—位移曲線如圖2所示。由圖2可以看出，濾波后轎廂位移均勻有序，符合索道正常運行特征。

4 結論

本文針對索道行業中索道轎廂在線路上的定位問題，結合GPS定位的特點，計算出各個轎廂以索道站房為坐標原點的相對定位，通過卡爾曼濾波器對相對定位的東西分量和南北分量分別濾波，同時考慮到索道走向對濾波系數的影響，為不同走向的索道研制出一套相對定位的通用算法，既滿足了定位精準度，又保證了數據的實時性。其結果符合索道的運營要求，已經成功應用于索道行業，為國內多條索道的運營提供了幫助。

表1 索道轎廂位移在濾波前、后數據對比

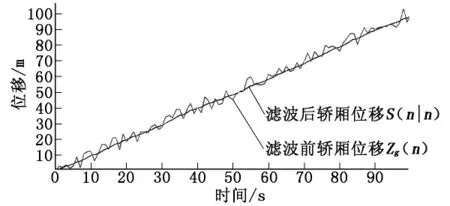
圖2 濾波前、后索道轎廂時間—位移曲線