基于卡爾曼濾波數據融合算法的智能釣魚竿系統①

陳小磊, 岳俊峰, 李秀梅

(杭州師范大學 信息科學與工程學院, 杭州 311121)

釣魚作為一項考驗技術、耐力、經驗的戶外運動,已經被越來越多人所接受, 而釣魚活動中最重要的工具就是釣魚竿, 傳統釣魚竿往往需要通過長時間的釣魚活動訓練和長時間盯著魚漂才能看漂識魚, 極大地降低了釣魚的樂趣.目前市場上加裝傳感器的魚竿一定程度上彌補了傳統釣魚竿的不足, 但此類釣魚竿依然存在很多缺點: (1)檢測裝置單一, 缺乏水域監測能力.(2)抗干擾能力較差, 有魚咬鉤時, 報警信號誤報率較高, 咬鉤時不能準確報警.(3)不具備自動遛魚功能,斷線跑魚概率較大.

針對上述情況, 本文利用多種傳感器和MCU 控制器及外圍硬件電路, 通過嵌入式技術和自動化控制技術, 研究一種具有智能選釣位、智能報警及自動遛魚等功能的新型智能釣魚竿系統.該智能釣魚竿系統將有助于提高釣魚的精確度, 同時提供一種自動化釣魚方案, 為在惡劣環境下完成自主釣魚活動提供可能.本系統基于卡爾曼濾波的數據融合算法對四元數法解算得到的魚竿姿態角數據進一步修正, 最優魚竿姿態角是智能報警和智能遛魚功能實現的關鍵.因此本文主要研究魚竿姿態解算過程、姿態數據濾波算法及魚竿自動遛魚控制算法等內容.魚竿姿態解算、控制系統數學模型以及串級PID 控制算法的仿真測試結果表明, 控制系統響應良好.在uC/OS-II 操作系統下, 環境傳感器及姿態傳感器的數據解算實時性良好, 例如魚竿報警功能, 具有較高靈敏度和準確率, 符合預期目標.

1 智能釣魚竿系統總體方案設計

智能釣魚竿主要由8 個部分組成, 如圖1 所示, 其中① 為魚竿桿體, ② 為負責收放線的紡線輪, ③ 為環境檢測部分, 該部分主要由溫度傳感器、光線傳感器、溶解氧傳感器及深度傳感器所組成, 該部分將負責測量待釣水域的環境信息以作為釣位選擇的依據, ④ 為姿態傳感器部分該部分主要由陀螺儀傳感器、加速度計傳感器及磁力計傳感器所組成, 該部分主要功能為獲取魚竿姿態, ⑤ 為魚竿手柄該部分, ⑥ 為魚竿控制部分, 該部分由STM32 控制器、電機驅動、電機及報警模塊組成, 為智能釣魚竿控制部分的核心, 其通過魚竿姿態的變化來實現智能釣魚竿的報警及遛魚功能, ⑦ 為電源模塊.該模塊主要負責為整個系統供電.⑧ 為魚線.

釣魚竿智能選釣位功能的實現是通過將溫濕度傳感器、光線傳感器、深度傳感器、溶氧量傳感器及微控制器集成于一個防水球體內, 在釣魚時, 將此可拆卸的球體隨釣魚鉤一起投入待釣水域, 通過球體內的微控制器及傳感器采集待釣水域的溫度、光線、深度及含氧量等數據, 并通過數據分析預判該水域是否適宜魚逗留, 進而實現智能選釣位的功能.

圖1 智能釣魚竿示意圖

釣魚竿智能報警功能的實現是通過在釣竿頂部安裝姿態傳感器, 通過姿態傳感器中的三軸加速度計采集加速度數據, 三軸磁力計采集磁場數據, 三軸陀螺儀采集角速度數據, 微控制器分別對三軸陀螺儀和三軸加速度計采集到的角速度數據和加速度數據通過卡爾曼濾波算法進行數據融合, 轉化為歐拉角進而獲取釣竿姿態.當魚有咬鉤信號時, 魚竿會有向下的瞬時加速度, 同時魚竿發生形變即會有一定的傾角變化, 此部分功能將通過瞬時加速度及魚竿姿態變化傾角作為報警信號, 通過高精度姿態傳感器獲取魚竿姿態變化, 能更加有效的捕捉到魚咬鉤的輕微信號, 這將極大地減少誤判率進而改進目前市場大多魚竿報警率低的問題.

釣魚竿智能遛魚功能通過自動化控制技術實現,通過測量及預判魚線實時拉力值, 建立魚竿物理模型,利用魚竿姿態傾角變化來驅動電機, 可有效控制魚線收放過程, 使遛魚過程中魚線始終處于魚線的最佳拉力值附近, 從而減少斷線跑魚的概率, 實現智能遛魚功能.

2 智能釣魚竿系統硬件部分設計

智能釣魚竿系統硬件部分設計框圖如圖2 所示.本文選用STM32F103ZET6 微控制器作為智能釣魚竿核心控制器, 溫濕度傳感器DHT11 和光敏電阻模塊作為環境傳感器, MPU6050 六軸加速度/角速度傳感器作為魚竿姿態采集模塊, TB6612FNG 作為直流減速電機驅動模塊, 12 V 聚合物鋰電池作為電源模塊.

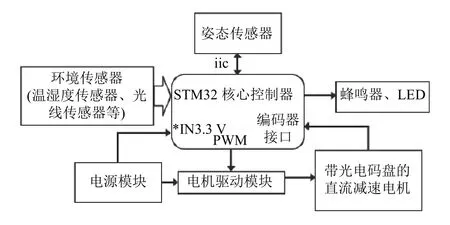
圖2 智能釣魚竿系統硬件部分設計框圖

3 智能釣魚竿系統軟件部分設計

本部分主要完成以下內容: (1) 四元數法解算魚竿姿態; (2) 通過建立卡爾曼濾波算法的狀態方程和觀測方程實現基于卡爾曼濾波的數據融合算法; (3) 建立串級PID 算法模型, 并通過Simulink 仿真整定PID 參數,進而實現智能釣魚竿的控制.

為了實現智能遛魚功能, 魚竿電機控制流程如圖3,通過加速度和磁力計得到的姿態角作為卡爾曼數據融合算法的測量值, 將陀螺儀傳感器得出的姿態角作為預測值, 通過卡爾曼濾波數據融合得到精準姿態角.將由數據融合的到的姿態角作為串級PID 算法的輸入量, 通過外環角度PID 和內環角速度PID 算法求出電機控制調節量, 通過電機驅動來控制電機轉向和轉速.

圖3 魚竿電機控制流程圖

3.1 四元數姿態解算

四元數法是比較常用的姿態解算方法, 通過引入一個四維空間超復數, 當實部為零時, 建立了四維空間和三維空間的聯系, 由于角速度積分有累計誤差的特性, 因此需要借助加速度分量對四元數矩陣進行修正,再利用四元數和歐拉角的轉換公式即可計算出歐拉角.

圖4 為智能釣魚竿四元數姿態解算的流程圖.首先初始狀態下, 由四元數和歐拉角的關系確定初始四元數, 姿態傳感器采集原始數據并通過均值濾波方法過濾掉高頻信號, 然后將四元數的等效余弦矩陣中的重力的分向量歸一化后進行向量的叉積運算, 進而求解出陀螺儀的積分誤差, 得到準確的角速度后采用一階龍格庫塔法更新四元數和姿態矩陣, 將四元數歸一化后即可轉換出歐拉角.

圖4 四元數姿態解算流程圖

3.1.1 四元數定義

四元數是一個復數由實部和虛部組成, 四元數的虛部包含3 個虛數單位i、j、k, 即四元數可以表示為:

其中, 復數間有以下關系:

四元數的矩陣表示形式為:

在三維坐標系中, 用四元數表示繞著某個軸的旋轉公式可用式(6)來表示, 其中, α 表示繞軸旋轉的實際角度, cos(βx), c os(βy)和 cos (βz)表示定位旋轉軸的方向余弦.當四元數的范數滿足時, 稱該四元數為單位四元數.該約束條件建立了三維和四維空間的聯系, 可以利用四維空間的四元數性質和運算規則來解決三維空間中的旋轉問題.

3.1.2 四元數微分方程q0, q1, q2, q3是時間的函數.可建立四元數微分方程如下:

由于對象是運動的, 所以四元數Q 是個變量, 即

其中, ω 為沿坐標系的角速度.

將上述公式展開:

姿態矩陣角速度 ω= [ωx,ωy,ωz]T可通過陀螺儀測量值經過補償后得到.

3.1.3 四元數姿態矩陣關系

四元數轉換成方向余弦矩陣: 設有參考坐標系e,鋼體坐標系為b, 假設初始狀態e 坐標系與b 坐標系重合, 則通過四元數可以得出b 坐標系旋轉至e 坐標系的轉換矩陣, 坐標轉換矩陣公式見式(9)[1]:

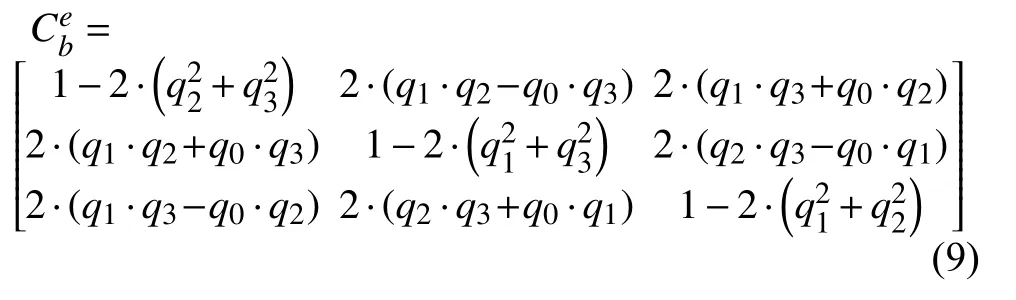
通過式(10)可求出由b 坐標系轉換至e 坐標系的坐標(Xe,Ye,Ze).

從方向余弦矩陣歐拉角的轉換: 設魚竿的偏航角為 ψ, 俯仰角為θ, 翻滾角為 φ, 假設導航坐標系為g, 則剛體坐標系b 與導航坐標系e 的關系如下[2]:

我們認為:

由于在坐標系在旋轉過程中坐標系一直保持正交關系, 所以有為正交矩陣:

由式(13)和(14)得:

由式(14)和式(15)通過上述公式變換即可解算出載體的姿態角得出:

3.1.4 初始四元數

設三軸加速度計和三軸磁力計在靜止條件下的初始姿態角為( ψ, θ , φ).有:

由式(13)和式(17)可得:

由式(18)即可得出初始四元數.

3.1.5 更新四元數

四元數的更新常采用一階龍格-庫塔法算法來實現[3], 一階龍格-庫塔法的解為:

進而可推出:

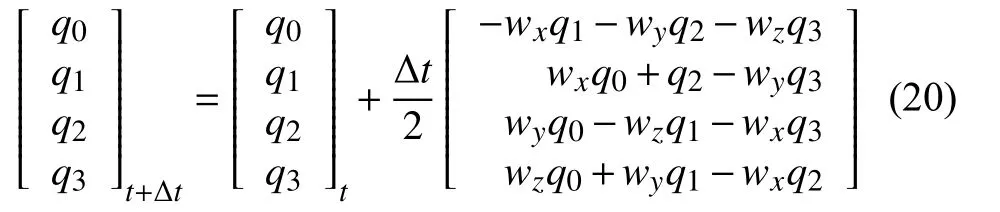
設 gx、 gy、 gz為陀螺儀傳感器測量的角速度, 設T 為姿態更新時間, 則由四元數微分方程的求解公式可得更新后的四元數:

3.1.6 四元數轉換歐拉角

計算當前時刻的四元數Q (t+T), 并對其進行歸一化處理:

設四元數[q0q1q2q3]的模為mode, 則:

由式(24)可得姿態角為:

3.2 卡爾曼濾波算法

作為一種高效的自回歸濾波器, 卡爾曼濾波常用于解決離散的線性系統濾波問題.卡爾曼濾波通過最小均方差來衡量最佳估計的標準, 算法的實現是通過求解狀態方程和觀測方程然后不斷的更新最小均方差,進而得出最優估計.

3.2.1 狀態方程和觀測方程

一個常規的線性離散系統模型, 其狀態空間方程如式(26)所示:

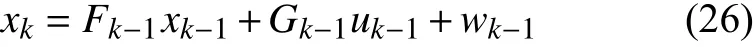
其中, Fk-1為 k-1 時刻對應狀態轉移系數矩陣; Gk-1為k-1 時刻對應控制輸入的增益矩陣; w 為過程噪聲.

觀測方程如下:

其中, zk表示k 時刻的觀測值; H 表示測量系數矩陣;vk表示觀測噪聲.

狀態方程中的噪聲w 和測量噪聲v 默認情況下認為兩者是相互獨立且滿足高斯分布的白噪聲, 即:

為了在實際使用中簡化算法, 常假設噪聲協方差矩陣Q 和測量噪聲協方差矩陣R 均為定值.

3.2.2 卡爾曼濾波算法流程

卡爾曼濾波算法在數學方法中是一種遞歸預測法,以偏差的最小方差為標準, 計算得到系統的最優估計值, 具有較好的實時性和抗干擾性[4].卡爾曼濾波算法是通過測量過程和預測過程間的相互更新相互反饋并通過求解卡爾曼增益和更新狀態方程來實現系統的自回歸狀態估計, 進而求出系統的最優估計.卡爾曼濾波器可分為時間更新方程和測量更新方程.

式(30)和式(31)為卡爾曼時間更新方程:

式(33)和式(34)為狀態更新方程:

狀態更新方程中, K 為濾波增益矩陣即卡爾曼增益, { zk-Hxkˉ}為觀測值和預測觀測的殘差, 和卡爾曼增益K 一起修正先驗預測, 更新狀態估計, 利用先驗估計誤差的協方差矩陣更新 Pk, 以備下次自回歸運算使用.

3.3 基于卡爾曼濾波的數據融合算法

由于三軸陀螺儀是通過角速度的積分獲得姿態角,存在隨機漂移誤差和常值誤差, 隨著時間的增加, 必然會使輸出誤差也積累增加, 因此單獨使用陀螺儀進行姿態解算無法獲得準確的姿態角.加速度計只有在靜止或勻速狀態下通過測量重力場, 可以準確計算出姿態角, 但是在實際情況中加速度計通常處于動態環境中, 因此單獨使用加速度計解算出的姿態角同樣不可靠.由于外界磁場的干擾, 單獨使用磁強計計算出的偏航角同樣存在誤差.為解決上述問題, 很多控制領域的專家做了大量研究, 并提出多種組合測量的方案[5], 結合本文需求及精確度要求, 本文結合卡爾曼濾波的遞歸預估特性, 采用一種基于卡爾曼濾波的數據融合算法.

3.3.1 狀態方程的建立

狀態方程的建立是將陀螺儀輸出的角速度通過四元數微分方程計算姿態角的過程, 作為當前狀態的預測.通過四元數微分方程求出的姿態角, 將作為當前預測值.姿態角的詳細計算過程已經在3.1 節四元數姿態解算中詳細敘述, 所以這里只給出相關公式:

四元數微分方程:

其中, ω 為沿坐標系的角速度.

將式(35)展開:

通過四元數歸一化可求出當前時刻姿態角(俯仰角、翻滾角、偏航角).

由卡爾曼濾波經典狀態方程可知預測值包含真實角度和誤差角度, 所以這里我們將所求的姿態角作為真實角度和誤差角度的合成, 用公式可表示為:

3.3.2 觀測方程的建立

將由加速度計和磁力計測量出的實際姿態角作為觀測量.

3.3.3 姿態角噪聲估計計算方法

在實際卡爾曼濾波器應用過程中, 過程噪聲協方差Q, 即作為預測姿態角的陀螺儀獲取姿態角的過程誤差協方差矩陣, 通常不容易得到, 但可以通過實驗的方法計算得到.測量噪聲協方差R, 即作為測量姿態角的加速度計和磁力計的噪聲協方差矩陣, 通過分析得到包含測量噪聲的數據, 測量噪聲協方差R 可以通過數據的融合更新得到, 具體計算過程如下:

將上面兩式相減, 即可得到兩時刻的融合誤差:

求融合誤差協方差:

由于陀螺儀、加速度計和磁力計的誤差為相互獨立, 即自相關性為0, 滿足:

則由式(41)～式(43)經過化簡及近似取代可得誤差協方差的最終結果為:

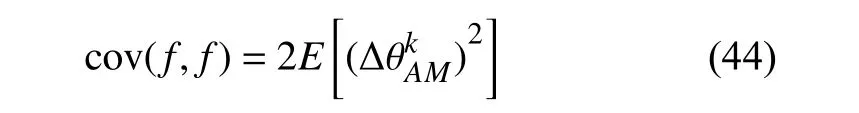
則得加速度計和磁力計的協方差R:

通過以上計算得出的測量噪聲協方差R, 用于卡爾曼濾波的自回歸數據更新, 經過反復優化迭代, 進而得到最優姿態角.

3.3.4 算法流程

(1)初始化參數, 記初始狀態k=1, 在六軸MPU6050傳感器處于靜止狀態下, 通過陀螺儀、加速度計和磁力計獲取初始角度.

(2)當k=2 時, 根據陀螺儀的角速度數據, 通過四元數法進行姿態解算預測當前角度, 根據前期陀螺儀數據實驗求得先驗誤差協方差 Pkˉ.

(3)按照式(32)求出卡爾曼增益K.

(4)根據k=2 時刻的加速度計和磁力計求出的姿態角作為觀測值, 按式(33), 式(34)實現預測值更新.

(5)計算k+1 時刻的預測值.實現方法: 通過采集k+1 時刻的陀螺儀輸出的角速度, 代入四元數微分方程求出此時刻的姿態角, 并作為預測值.然后循環執行步驟(3)和步驟(4).

算法流程如圖5 所示, 先對初始時刻采集的陀螺儀、加速度計和磁力計原始數據進行相應的濾波處理,若是初始狀態下, 那么將陀螺儀和加速度計解算出的姿態角作為初始姿態角, 并根據初始姿態角求出初始四元數, 然后將通過陀螺儀采集到的數據帶入四元數微分方程進而求出姿態角, 并作為估計角度, 通過采集加速度計和磁力計數據并通過計算求出的姿態角作為測量值, 可計算出過程噪聲協方差和測量噪聲協方差.利用卡爾曼濾波算法將預測角度和測量角度進行融合得到最優估計角度, 由卡爾曼濾波公式可知, 兩個符合高斯分布的數據融合后仍然滿足高斯分布且最優值處在融合后的高斯分布曲線, 因此可將每次計算出的姿態角作為下次融合的初始角, 反復的數據融合能夠得到一系列穩定的最優估計角度[7].

3.3.5 卡爾曼濾波數據融合算法的適用性

本文通過卡爾曼濾波數據融合算法輸出姿態角,而實際系統中總是存在不同程度的非線性因素, 利用線性化卡爾曼濾波方法, 通過不斷地統計和計算數據方差來自動改變卡爾曼增益系數K, 因此當系統存在噪聲或者預測量的累積誤差較大時, 也能提高系統精度, 誤差能夠通過快速迭代而減少.

智能釣魚竿中采用高性能單片機獲取高頻的姿態數據, 自動整定得到的卡爾曼增益系數具有較強的通用性, 同時計算量相對較大.智能釣魚竿系統中使用的STM32 微處理器能夠保證數據融合線程周期不超過100 ms, 較高的姿態融合頻率可以保證預測量誤差較小且收斂速度較快, 因而基于線性卡爾曼濾波的姿態數據融合能較好地完成對目標的濾波估計處理.

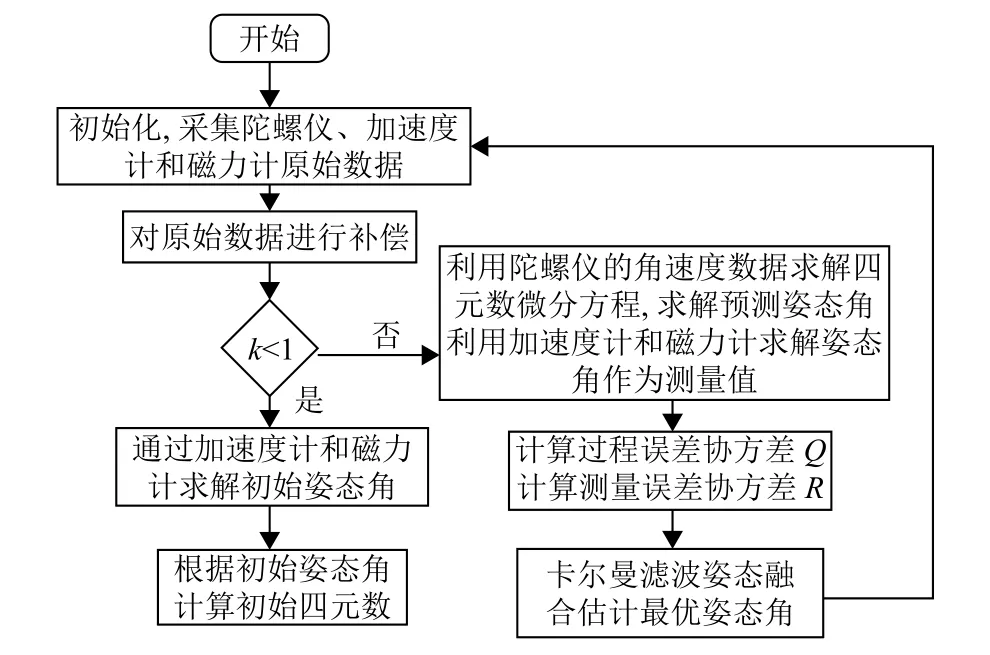
圖5 算法流程圖

3.4 基于PID 控制算法的智能遛魚控制方案

本文中所述魚竿是以電機轉動帶動魚竿紡線輪實現魚線自動收放線的智能釣魚竿.所謂遛魚, 指的是一種釣魚方法.釣魚時如果釣到個體較大的魚一般都不能直接將魚提上來, 魚勢必在被勾住后掙扎逃竄, 此時我們需要根據魚的力氣大小來選擇收線和放線, 在收線和放線的來回拉扯中, 逐漸消耗掉魚的體力, 當魚精疲力竭停止反抗時, 將魚拉回岸邊的這個過程, 形象地稱為“遛魚”.

通過上文中的姿態解算及卡爾曼濾波數據融合可得魚竿的實時姿態角, 結合圖6 對魚竿模型進行分析:當檢測到魚竿的俯仰角的傾角偏差大于或等于 θ1時判斷為有魚咬鉤, 此時系統開啟智能報警功能, 同時檢測遛魚功能是否開啟, 若開啟遛魚功能, 則將當前魚竿傾角偏差與偏差角 θ2做 比較, θ2為控制電機正反轉的臨界值, 當傾角偏差小于 θ2, 則需要控制器控制電機正轉, 達到收線的目的, 對魚竿和魚組成的力學模型分析可知,當魚竿加速收線時, 由于魚的重力及向反方向的拉力會使得魚竿傾角偏差不斷加大, 當傾角大于 θ2時, 則應控制電機反轉, 實現放線的目的, 當魚竿快速放線時,魚竿的傾角偏差會逐漸減小, 在魚竿的不斷循環往復的收放線的過程中實現消耗魚的體力的目的.θ3為魚線處于極限拉力值時魚竿所對應的偏差角, 當拉力值大于該魚線的極限拉力值時, 就會導致斷線跑魚, 所以在遛魚過程中對于收放線的時間和魚線拉力值的控制都有較高要求, 基于以上分析, 該控制系統需要通過角度的偏差來實現系統的控制, 因此本文采用串級PID 算法來實現智能遛魚功能.

圖6 魚竿傾角示意圖

3.4.1 串級PID 控制模型的建立

本文采用雙環PID 控制系統, 即外環采用角度環,內環采用角速度環, 角速度環的加入將更加準確的表示魚竿姿態, 使控制系統更加穩定.與傳統的單環PID 控制器相比, 增強了控制系統對外界的抗干擾能力, 提高了控制精度.智能釣魚竿串級PID 控制流程圖如圖7 所示.

3.4.2 串級PID 控制系統Simulink 仿真

本文中采用以角度作為外環控制, 角速度作為內環控制的串級PID 與以角度作為控制量的單環PID 控制作比較.從而驗證串級PID 控制的優越性.在該系統仿真中輸入量為指定的角度, 輸出為經過串級PID 控制輸出的角度, 該系統將以階躍信號為輸入進行系統仿真, 通過參考飛行器的數學模型的推導, 在這里假設該俯仰角、翻滾角及偏航角的傳遞函數分別為:

可建立單級和串級PID 下俯仰角和翻滾角Simulink仿真結構如圖8.

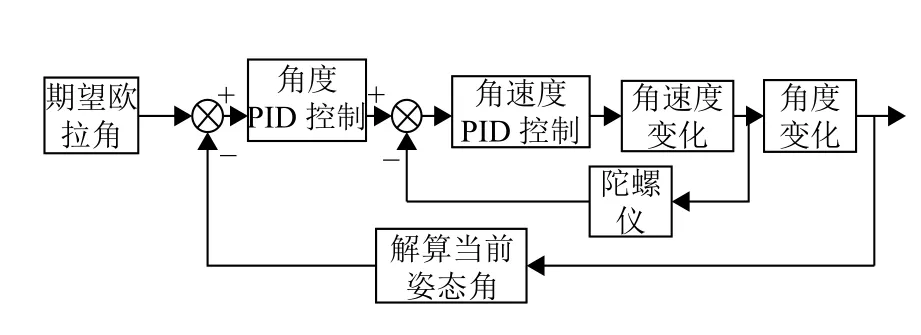
圖7 串級PID 控制流程圖

圖8 單級和串級PID 下俯仰角和翻滾角仿真結構圖

可建立單級和串級PID 下偏航角Simulink 仿真結構如圖9.

俯仰角、翻滾角的單極與串級PID 仿真結果對比如圖10 所示, 圖中紅線為單級PID 仿真波形, 藍線為串級PID 仿真波形:

偏航角的單極與串級PID 仿真結果對比如圖11所示.

由圖10 和圖11 仿真結果圖可見, 在輸入信號為階躍信號的控制系統中, 單極PID 控制下系統的超調量和振蕩次數明顯大于串級PID 控制下系統的作用,因此串級PID 控制系統下控制信號更穩定且響應速度更快.

3.4.3 PID 參數整定

本節采用試湊法對串級PID 參數進行整定.試湊法是根據以往經驗依照先內環、后外環、先比例、后積分再微分的步驟來實現參數整定.由于參數整定過程類似, 本節以俯仰角為例進行調試.

首先整定內環PID 參數, 比例參數Kp=4 時, 此時系統振蕩劇烈, 系統嚴重超調, 此時應減小Kp 的值.Kp=1 時系統需要很長時間才能恢復到1 值, 說明Kp 值偏小, 因此可初步判斷Kp=3 時較為合適.但是單純的比例調節無法使系統快速穩定, 還應加入積分調節, 調節依據是若系統誤差消除較慢, 此時應當適當減少積分時間, 增強積分作用.此時系統可以較快的消除誤差, 但系統超調量較大, 此時應加入微分作用減少超調量, 加入微分控制量能一定程度上抑制超調量.

圖9 單級和串級PID 下偏航角仿真結構圖

圖10 俯仰角和翻滾角仿真結果對比圖

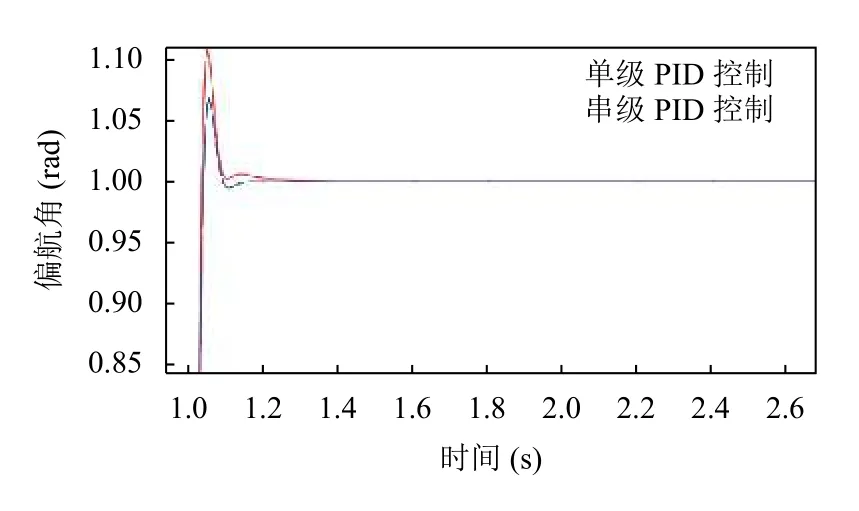
圖11 偏航角仿真結果對比圖

由于PID 參數的調試是一個參數間相互耦合的過程, 所以在調試中要不斷的嘗試和試湊才能得出最終理想的參數.通過反復試湊的方法, 最終確定智能魚竿PID 控制參數如表1 所示, 最終俯仰角的PID 仿真結果圖如圖12 所示.

由最終的串級PID 仿真圖, 可知系統在階躍信號輸入的控制系統中, 響應時間約為0.03 s, 系統穩定時間約為0.1 s 且系統超調量在10%以內, 因此該串級PID 控制系統能夠快速響應并快速趨于穩定, 能較好地實現魚竿的控制需求.

表1 智能魚竿PID 控制參數表

圖12 俯仰角PID 最終仿真結果圖

4 智能釣魚竿系統測試結果

智能釣魚竿系統實物圖如圖13 所示, 考慮到魚竿對輕便的需求, 經過調試, 實現了智能釣魚竿的相關基本功能, 如智能報警功能.該智能釣魚竿設計成本低廉且功能實用, 具有較好的實用價值和廣闊的市場前景.

4.1 姿態角測試結果

由姿態傳感器數據處理得到精確的姿態角是控制系統的基礎, 其測量結果的準確性對于實驗結果準確性有很大的影響.

由于陀螺儀和加速度計均存在不同頻段的噪聲而導致在檢測過程中產生一定的誤差, 所以本系統采用了卡爾曼數據融合方式來降低誤差, 圖14 為傳感器靜止時, 最終解算出的歐拉角波形.

圖13 智能釣魚竿整體實物圖

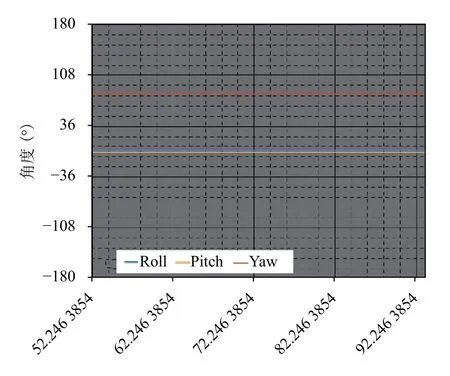
圖14 靜止時解算的姿態角波形圖

由圖14 可知, 藍色曲線表示翻滾角, 黃色曲線表示俯仰角, 紅色曲線表示航向角, 傳感器水平靜止放置時, 姿態角的初始值曲線相對平滑且俯仰角和翻滾角角度均接近零, 說明本文中通過卡爾曼數據融合算法最終得出的姿態角相對精確且噪聲較小.

圖15 為智能釣魚竿實際運行時姿態角變化波形圖, 航向角的量程范圍為-180°到+180, 則從-180°變化到+180°時, 角度會突變.由圖可知在7-8 s 的時間段內Yaw 出現了從-180°到+180°的突變, 因此在智能釣魚竿姿態控制時會對該處進行平滑處理.

圖15 角度突變時解算的姿態角波形圖

4.2 智能魚竿報警功能測試

智能魚竿的報警是依據俯仰角的變化作為咬鉤信號的判斷, 當魚竿俯仰角的變化在10 度以上時, 則認為此時有魚咬鉤, 且可以通過調節報警閾值來改變智能釣魚竿報警的靈敏度.對測試數據進行統計得出表2.

分析表2 可知, 當翻滾角和偏航角保持不變時, 俯仰角度變化大于10 度時魚竿報警, 俯仰角變化小于10 度時, 魚竿不報警, 當俯仰角度不發生變化時, 無論翻滾角和偏航角如何變化, 魚竿均不報警, 且由表中數據分析可知魚竿傾角變化在較接近10 度時依然可以很準確的發出報警信號, 這也從側面證明姿態解算出的姿態角精度較高.

表2 魚竿報警數據分析表

5 結論與展望

本文以微處理器STM32 為核心搭建uC/OS-II 操作系統, 通過四元數法對魚竿姿態解算, 提出基于卡爾曼濾波的數據融合算法, 并以串級PID 控制算法實現了魚竿控制系統的智能控制, 并通過Matlab 建立Simulink仿真, 驗證了串級PID 控制器的有效性.通過實驗測試最終達到了本設計的預期功能.