基于Grasshopper的汽車格柵CAS模型參數化設計

王立宏

(北京現代汽車有限公司，北京 101300)

0 引言

參數化設計最早在建筑領域應用較多，目前已有大量實際建筑應用，國內比較著名的參數化建筑有鳥巢及水立方等。隨著參數化設計工具的推廣及現代制造工藝的進步，越來越多的汽車上出現了參數化造型特征，其中汽車前格柵最易被參數化設計，如圖1所示的奔馳CLA參數化造型前格柵，稱之為“滿天星”，通過小六邊形的亮點圍繞著奔馳三叉戟圓形LOGO及前格柵邊框有規律地排布，營造出緊致而又精致的美感，為整體造型錦上添花。對于“滿天星”等參數化造型特征，傳統的建模方式可實現，但無論是初次建模還是后期方案推敲修改，均避免不了大量的手工操作，嚴重影響造型開發效率。合理運用參數化設計可很大程度上提高CAS建模速度，縮短造型開發周期。

圖1 奔馳CLA

1 參數化設計優勢與工具介紹

1.1 參數化設計優勢

參數化設計(Parametric design)目前還沒有一個廣泛認可的定義，一般理解為將某些重要因素變成某個函數的變量，通過改變該變量值，改變函數結果，從而生成不同的方案。

(1)傳統設計的局限性

在傳統造型概念設計過程中，設計師通過頭腦風暴、聯想、比擬、仿生等思維創作汽車造型，產生出概念方案，選定方案效果圖后根據效果圖在三維軟件如Alias中搭建汽車三維模型，此過程稱為汽車CAS設計階段。在此階段經常會進行方案調整或者衍生出其他方案，但CAS設計師通過Alias軟件等手動調整方案或者搭建衍生方案時往往需要重新建模，耗費大量時間與精力，而設計師在等待CAS模型修改的時候也容易淡化創作靈感，創作思維不連續。

(2)參數化設計的優勢

參數化設計方法主要在CAS模型階段進行，通過構建邏輯規則，將主要的造型特征變量用參數驅動，通過更改參數可即時生成三維模型，并衍生出多個造型方案，模型具有逆向可調性，極大地縮減CAS模型搭建時間；同時設計師可直觀觀察對比各個衍生方案的優缺點，進行選擇或者二次創作，設計靈感不再隨機、創作思維得以連續。

參數化設計解決了傳統造型設計遇到的瓶頸，最重要的意義在于提高了效率，降低了成本，縮短了CAS建模時間，拓展了造型設計思路，有利于突破汽車造型的現有局面。

1.2 參數化設計工具介紹

目前參數化設計工具主要有Grasshopper、Dynamo等，其中Grasshopper功能強大、穩定性好，本文作者采用Grasshopper進行參數化模型搭建。

Grasshopper(下文簡稱GH)是一款在犀牛軟件環境下運行的采用程序算法生成模型的插件，是目前比較流行的參數化設計工具。GH把相關功能封裝在一個運算器內，這些運算器又稱為“電池”。GH將編程節點可視化，設計人員只需對運算器輸入某些參數，就可以得到相關結果，降低了設計人員的學習成本，不過仍需相關設計人員具有編程知識。打開犀牛軟件加載GH插件后的界面如圖2所示，運算器連接起來的圖也稱之為“電池圖”。

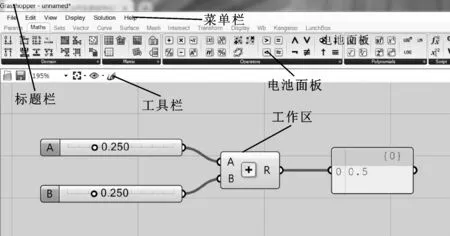
圖2 GH界面

使用某個運算器時直接將運算器從面板中拖入工作區，點擊運算器兩側的半圓可以將各個運算器連接起來，如圖2所示為加法運算器，左側A和B為輸入端，右側為輸出端，輸出運算后結果。

2 格柵CAS模型參數化設計

汽車前格柵作為汽車前臉造型非常重要的部件，在造型設計中一直處于十分重要的地位，很多車型的家族化特征主要由其前格柵定義，如雷克薩斯紡錘形前格柵、寶馬雙腎形前格柵。

點陣式格柵是前格柵的常見形式，一般由基本的造型單元通過復雜的排列組合實現，如沿二維平面分布、圍繞中心布置、旋轉縮放等，此類排列組合是有規律的，可以通過調節某些參數實現。下面通過某個點陣式前格柵的建模簡述通過GH實現參數化設計的過程。

2.1 格柵參數化設計邏輯分析

圖3為點陣式前格柵的方案圖，可以看出，基本造型單元為一個梯形體，除了中間部分其他造型單元均有規律排列，通過陣列可以在平面上實現。但一般前格柵造型單元空間排列都比較飽滿，側面看是向外鼓出的，基本造型單元趴在一張空間立體面上，采用常規建模方法在平面陣列完成后，仍需要手動或者通過其他方式將其排列到空間位置，耗費很多時間；在推敲此方案時，如增多幾行幾列或者排列角度再變化一些，手動建模繁瑣耗時。

圖3 前格柵效果圖分析

經過分析，正面看，造型排列如圖3中虛線所示，基本的梯形造型單元可以在Alias中手動完成，造型單元排列比較復雜，趴在了一張空間曲面上，在GH中實現比較方便，基本邏輯順序見圖4。

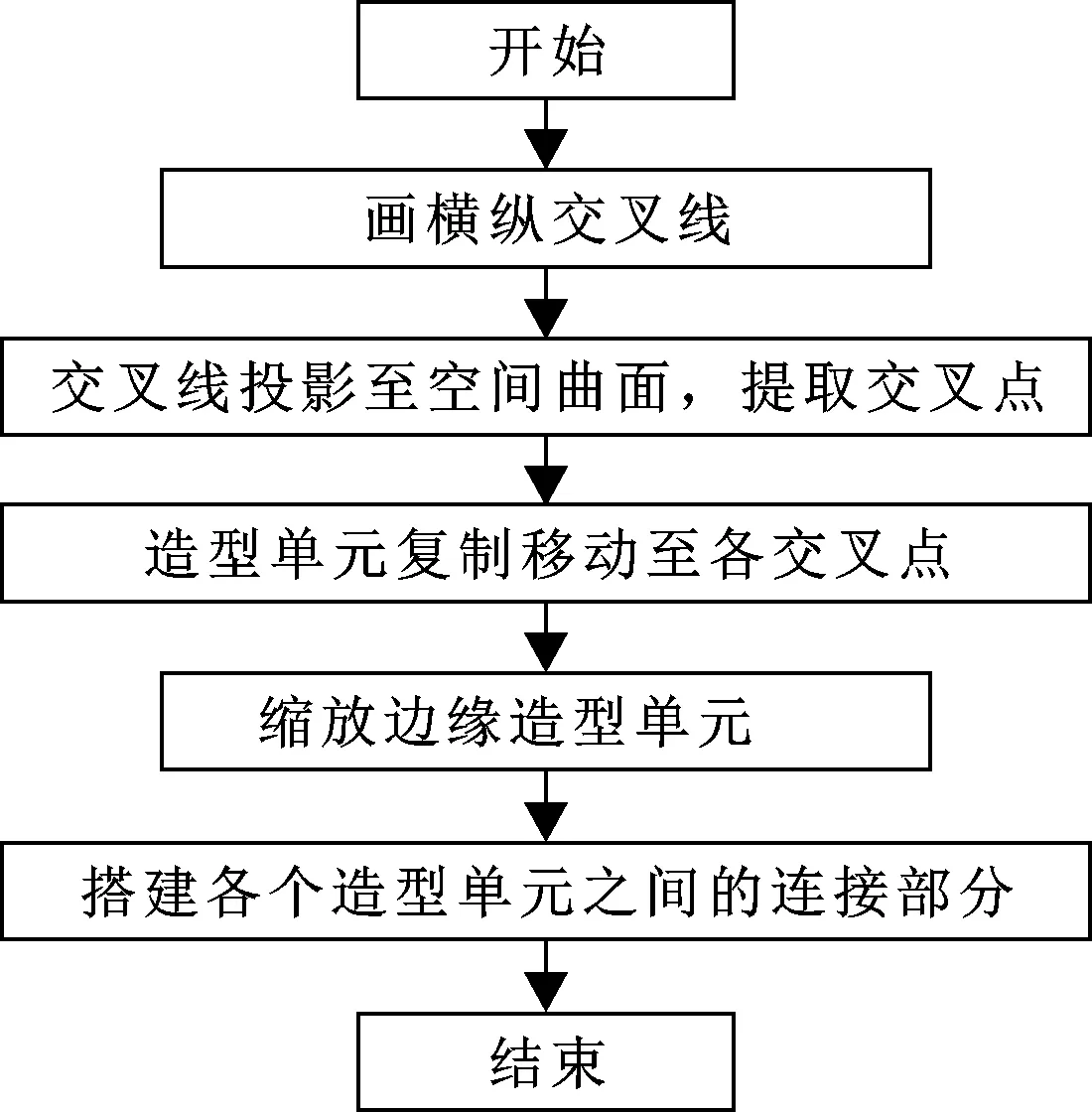
圖4 格柵參數化設計邏輯

下文即按圖4中邏輯順序在GH中一步步搭建出格柵。

2.2 畫縱橫交叉線

通過3個點畫出一條NURBS曲線，作為橫條，按Z方向陣列(Linear Array運算器)6個，同理做出豎條并陣列，陣列后每根豎條曲線繞著一端端點轉動(Rotate 3D運算器)某個角度，離Y0線越遠的曲線轉動角度越大，每個線的轉動角度可由等差數列實現，電池圖如圖5所示，“犀牛”里生成的曲線如圖6所示。

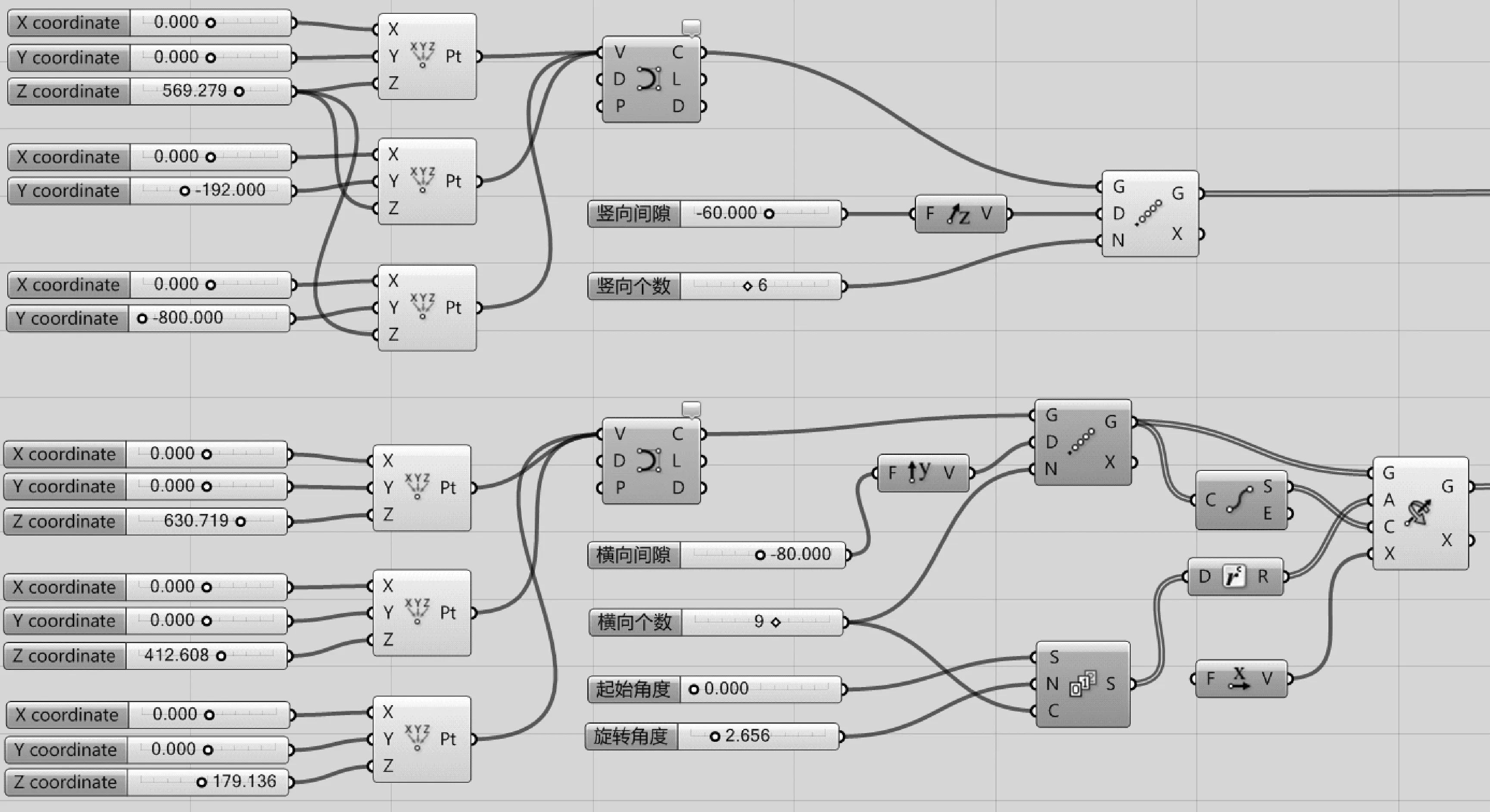
圖5 畫縱橫交叉線電池圖

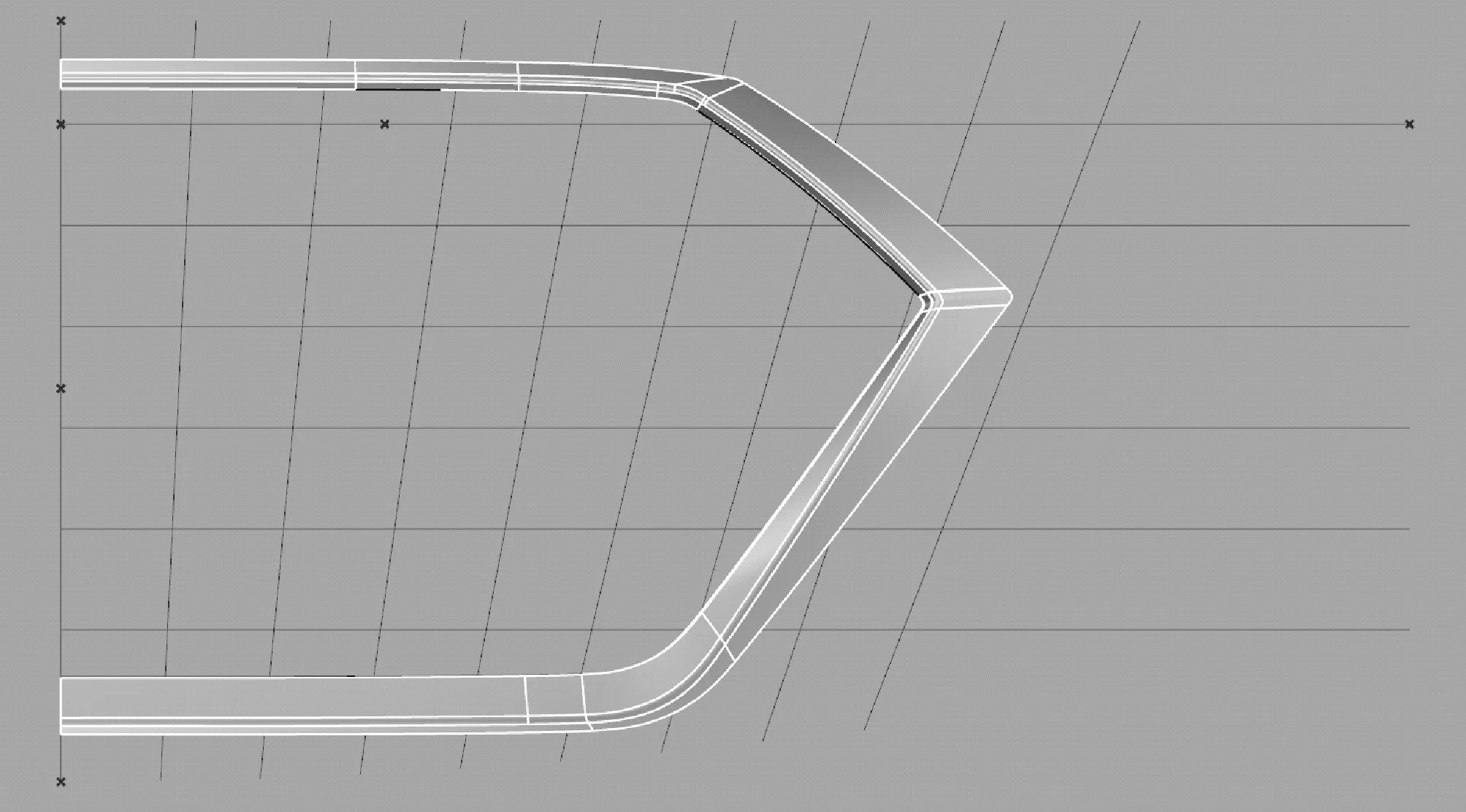
圖6 “犀牛”里中生成的縱橫交叉線

2.3 交叉線投影至空間曲面，提取交叉點

將上一步中生成的橫縱線投影至指定的曲面，提取交點，用Point List運算器可顯示各個點的編號，再使用分流運算器(Dispatch)，輸入端P的參數為布爾值TRUE、FALSE，即第0個點對應TRUE，分流至輸出端A；第1個點對應FALSE，分流至輸出端B；第2個點對應TRUE，分流至輸出端A；第3個點對應FALSE，分流至輸出端B。以此類推，從中篩選出想要的點，作為格柵每個造型單元最后要移動到的位置點。此案例中要用到的點為A端輸出的點，即序號為0、2、4、6、......的偶數點。相關電池圖見圖7，犀牛里生成的圖像見圖8。

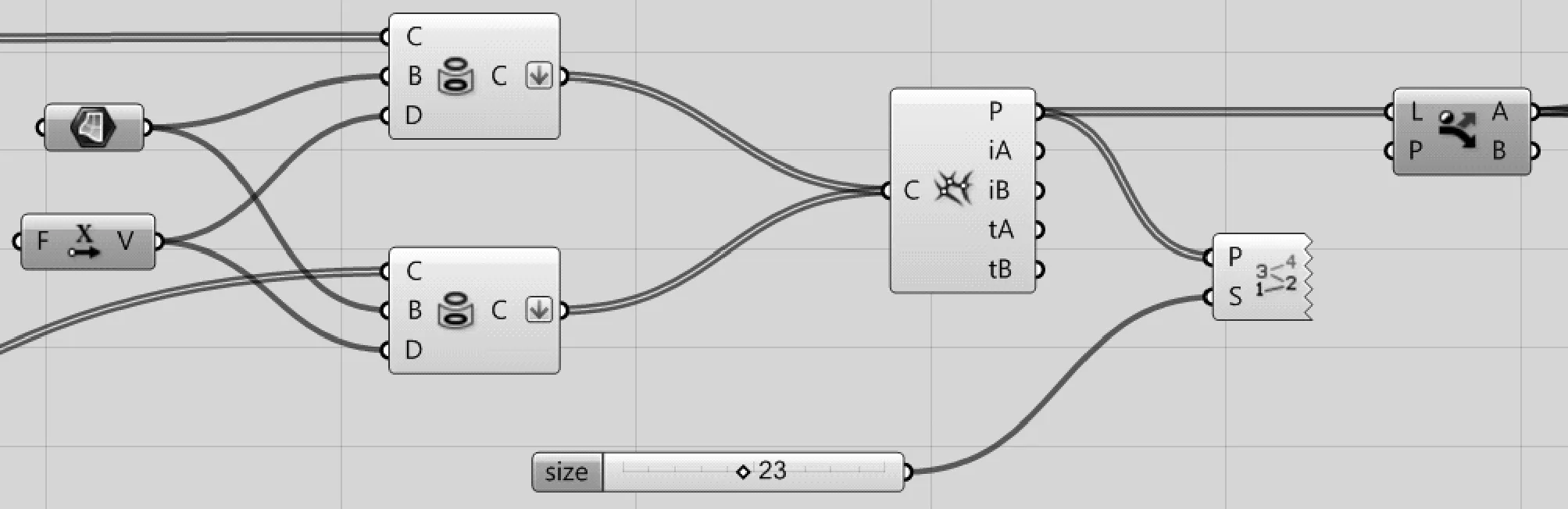
圖7 投影并提取交叉點電池圖

圖8 投影并提取交叉點后的模型

2.4 造型單元復制移動至各交叉點

找好造型單元要移動到的位置點后，把造型單元復制移動到對應的位置點即可，但在實現復制移動前，為了方便調整，此處增加兩項功能：(1)縮放功能，即圖9中A區域電池圖，對應圖10(a)；(2)移動功能，即圖9中B區域電池圖，對應圖10(b)，以后可通過調整此處，實現整體排列多樣化。GH中移動物體需要指定移動向量，圖9中C區域的提取向量起始點對應圖10(c)，Vector 2P運算器將C區域提取的向量起始點與圖8篩選后的點合成移動向量，之后造型單元(見圖11)按這些向量移動即完成復制移動，生成格柵主體。圖9中D區為顯示向量，對應圖12中箭頭，圖9中E區為移動運算器，對應圖12中造型單元。

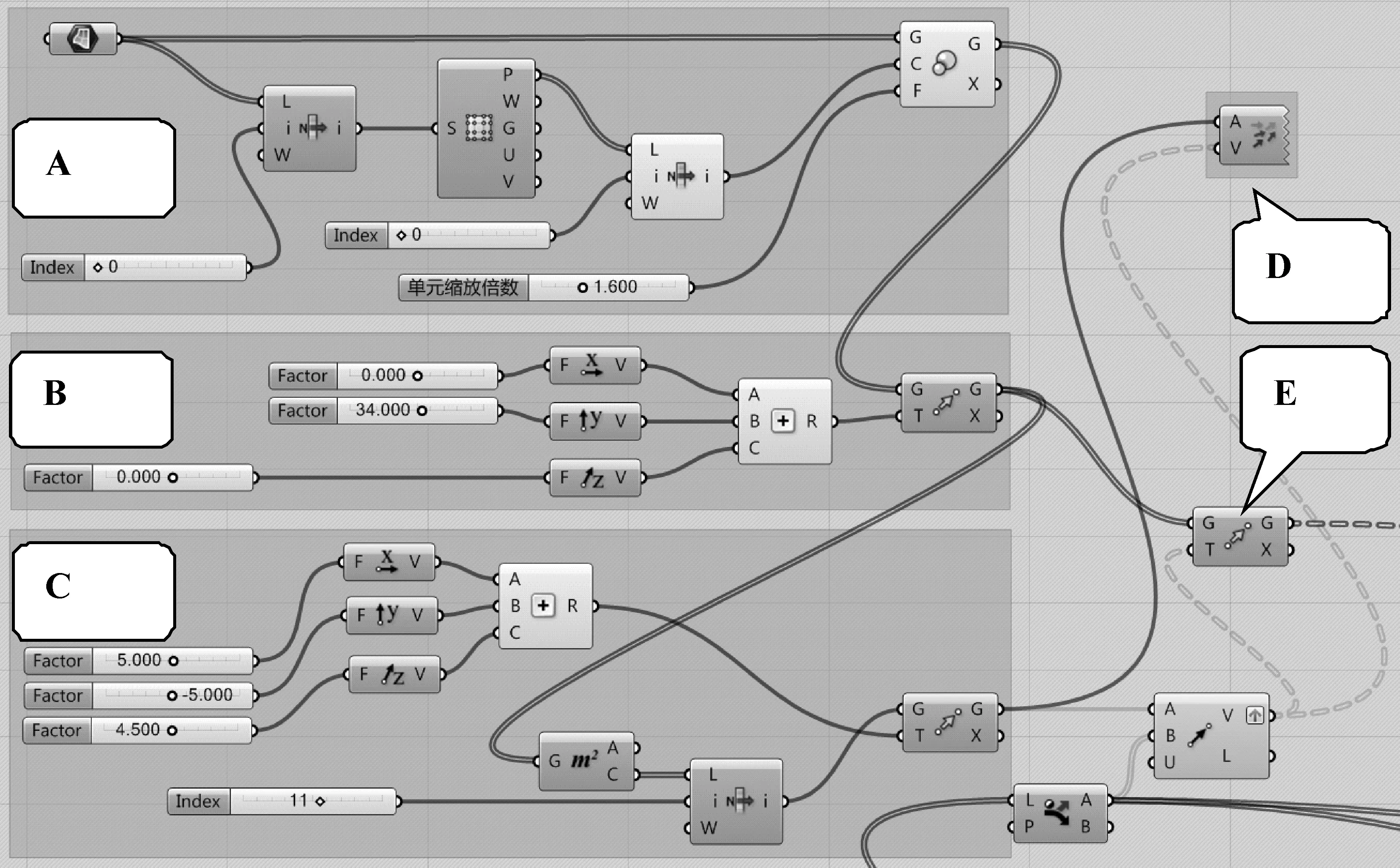
圖9 造型單元復制移動至各交叉點電池圖

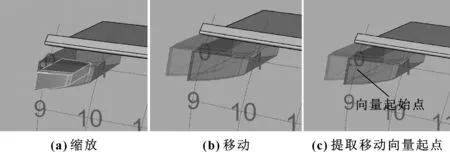
圖10 A,B,C區域電池圖模型

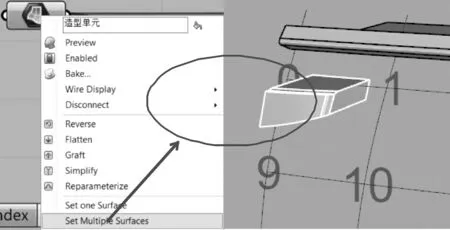
圖11 選取基本造型單元

圖12 復制移動造型單元

2.5 縮放邊緣造型單元

效果圖中為越接近格柵邊框的造型單元越小。可以提取格柵邊框上的線，稱之為干擾曲線，依次計算每個造型單元位置點到這條線的距離，以此距離除以某個合適的數值，作為各自造型單元的縮放倍數。為保證不至于縮放過于夸張，此處使用Minimum運算器和Maximum運算器將縮放比例限制為0.58～1，電池圖見圖13，生成的效果見圖14。

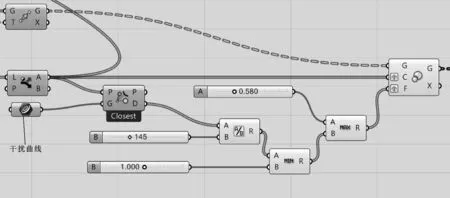
圖13 縮放邊緣造型單元電池圖

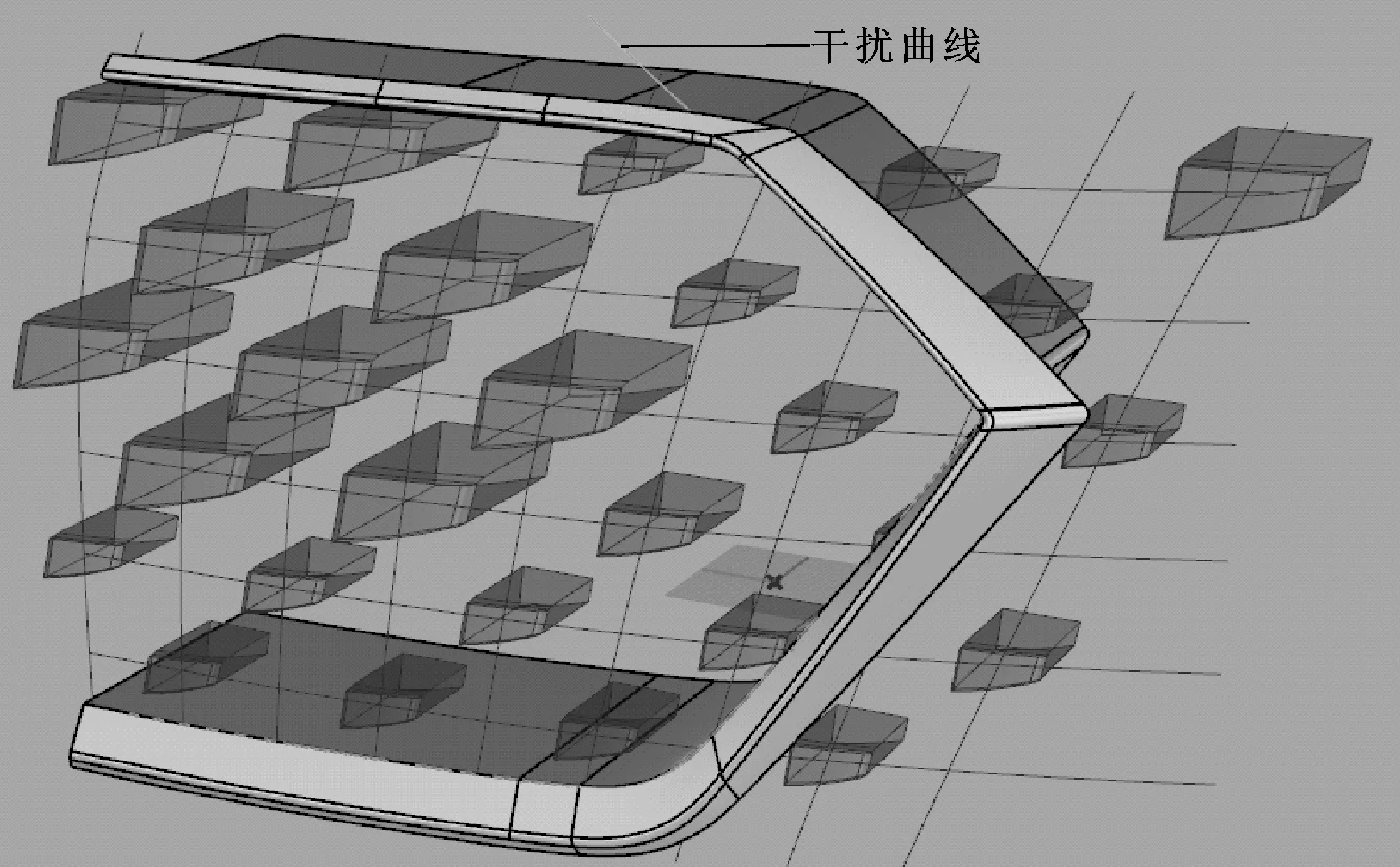
圖14 縮放后的模型

2.6 搭建各個造型單元之間的橋連部分

做各個造型單元之間的橋連部分。橋連分橫豎兩部分，此處闡述橫向橋連做法，豎向橋連做法一致，只是參數需要調整。橫向橋連基本思路為先畫出兩兩單元間的連線，觀察圖15可得，序號為0的造型單元右邊的點連接序號為1的造型單元左邊的點，需要提取兩組點，一組造型單元右邊的點，一組左邊的，兩組點提取過程一致，但兩點連線時須錯開一位造型單元(Shift運算器)，見圖16，否則出現圖17所示情況。

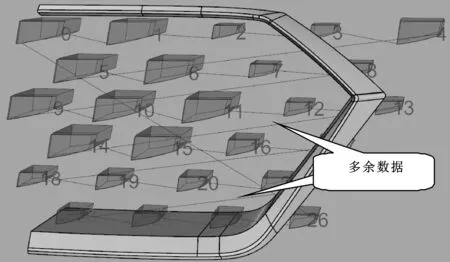
圖15 搭建好的橋連曲線

圖16 搭建橋連曲線電池圖

圖17 未錯開的橋連曲線

看圖15可得，每行換行處以及一頭一尾處出現了多余的數據，其長度明顯長于所需要的數據。此處進行分流，剔除較長的線，保留想要的線段，同時拉伸相關曲面做出完整的橋連結構，具體電池圖如圖18所示，同理調整相關數值做出豎向的橋接曲面，可得最后的結果如圖19所示。

至此，格柵主體部分已經完成，整理后如圖20所示，若要變化格柵行列數或者旋轉角度等通過調整相關參數即可，程序幾秒內自動輸出結果，相比在Alias里手動搭建格柵主體效率提升明顯，同時變化多端而又豐富規律的造型也激發設計人員的創作靈感，拓展了設計思路。圖21為通過調整不同參數衍生出的拓展方案。格柵主體在GH中創建，格柵邊緣裁剪部分在Alias中處理。

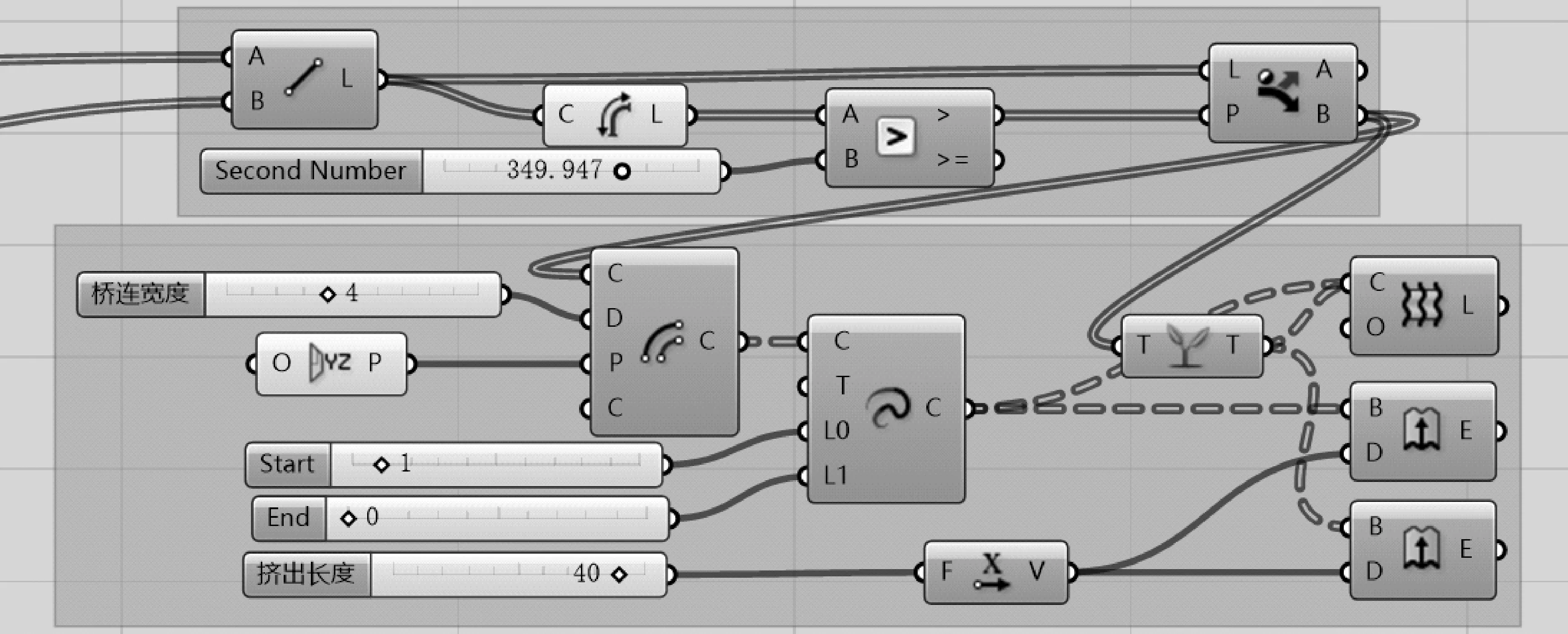
圖18 搭建橫向橋連曲面及擠出曲面

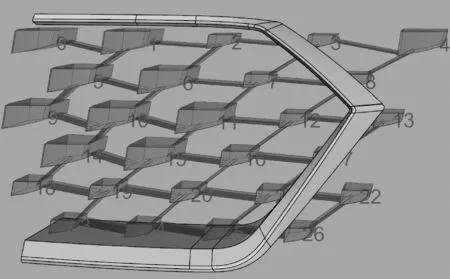
圖19 最終格柵

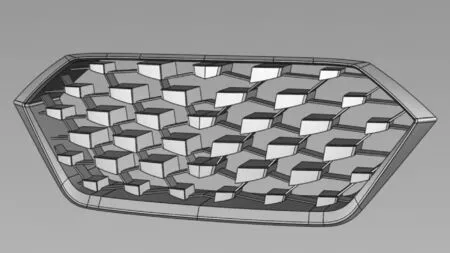
圖20 整理后的格柵模型

圖21 調整參數后的衍生格柵模型

3 結束語

運用參數化設計工具Grasshopper，給出點陣式格柵一般參數化建模思路和方法。在此基礎上應不斷創新，緊跟市場流行設計趨勢，及時高效地開發出具有未來感科技感的新造型方案。