基于干擾觀測器的逆變器在線死區補償*

馮振東，張力平，周 浩，欽 杰，藺宏良

（長安大學陜西省高速公路施工機械重點實驗室，西安 710064）

0 引言

近年來，功率開關器件如絕緣柵型場效應晶體管（MOSFET）和絕緣柵雙極型晶體管（IGBT）的飛速發展，使得應用矢量脈沖寬度調制技術的電壓源型逆變器得到了大量地應用。在理想三相橋式逆變電路中，每相橋臂的上、下2個開關管工作在互補狀態——上管導通，下管隨即關斷，反之亦然。然而在實際電路中，由于功率開關管開通時間通常大于關斷時間[1]。為了防止同一橋臂的上、下2個開關管同時導通造成直流電壓源短路，需要人為在開關管動作期間插入一段死區時間。

死區時間的長短由開關管和預驅電路參數確定，一般在1～5μs之間。嵌入死區時間引起的延遲可以防止上下橋直通引起的直流電壓源短路，但也會給輸出電壓帶來幅值和相位偏差。雖然在單個PWM周期內的電壓偏差并不大，但隨著開關頻率的提高，偏差電壓的累積將導致嚴重的輸出電壓畸變，從而導致輸出電流中奇次諧波增大，波形發生畸變。尤其是在低速輕載或者開關頻率較高時，死區所占比例較大，電機轉矩波動和電磁噪聲增大，直接影響系統穩定性[2-3]。

基于以上原因，國內外學者提出了多種補償策略來消除死區效應。其中最普遍的方式是利用平均誤差理論，根據死區時間計算出相應等效死區電壓，并根據電流極性補償到對應指令電壓中。該方法簡單易行，應用廣泛，但需要檢測電流極性。采用硬件電路進行電流極性檢測會增大成本，同時還會有檢測滯后和A/D轉換精度的問題[4]，所以目前多數采用軟件估算方法。軟件估算是通過電流重構，利用電流矢量角判斷電流過零點來估算電流極性，同時對坐標變換后的直流分量進行濾波可以減少濾波過程對電流幅值和相位的影響。但由于零電流鉗位、調制噪聲等的影響，直接判斷電流矢量角度難以確保電流極性檢測精度[5]，同時也忽略了功率器件開關延遲、飽和導通壓降和運行工況變化帶來的影響。針對上述問題，有學者提出新的補償策略，將死區效應、開關管動作延遲、飽和導通壓降等造成的擾動視作一個誤差電壓[5-7]，通過構建系統模型對其進行觀測，進行在線補償。

本文通過構建干擾觀測器（disturbance observer，DOB）的方式對擾動電壓在同步旋轉坐標系下的誤差分量進行觀測，采用一階低通濾波器濾除系統噪聲后將該誤差分量反饋到指令電壓，實現永磁同步電機控制系統在線死區補償。

1 死區效應分析

1.1 VSI死區效應

圖1為逆變器A相基本結構。Q1、Q2分別為上、下橋開關器件，D1、D2為對應橋臂上的反接續流二極管，其輸出連接到電機A相繞組。定義流出逆變器電流方向為正，流入逆變器電流方向為負。

圖1 逆變器A相橋臂基本結構

在理想工況下，控制逆變器上下橋臂的是互補PWM信號，在上管導通時，下管關斷，電流從直流電源正極經Q1流入A相，此時電流方向為正；反之，下管導通，上管關閉，電流從電機A相經Q2流入電源負極，電流方向為負。在加入死區時間后，死區時間段內，上下兩管都為關斷狀態，但是由于電機繞組中感性負載的作用，三相電流將通過續流二極管流動，iA＞0，電流經D2續流；iA＜0，電流經D1續流。所以在死區時間內，橋臂的輸出電壓將不受開關管控制，而是由相電流的極性決定。

圖2為電流極性為正時，單個PWM周期內開關信號分析。其中，Q1_pwm和Q2_pwm為互補的理想上下管開關信號。Q1_dt、Q2_dt是加入死區時間Td后的開關信號。Q1_actual、Q2_actual是同時考慮死區時間、開關管開通和關斷延時的開關信號，Ton為開通延時，Toff為關斷延時。

圖2 單個PWM周期開關信號

在一個PWM周期，由嵌入的死區、開關管導通和關斷延時造成的等效擾動時間可表示如式（1）。

A相實際輸出電壓與理想輸出電壓在1個周期內的平均誤差電壓計算公式如式（2）。

考慮開關管飽和壓降Vsat和續流二極管導通壓降Vdiode時，誤差電壓[7]計算公式如式（3）、（4）、（5）。

1.2 死區效應對輸出相電壓的影響分析

根據公式（2）（4）（5）可知逆變器施加到永磁同步電機上的相誤差電壓VAn,err、VBn,err、VCn,err分別如式（6）所示。

因為VA,err、VB,err、VC,err幅值都為Verr，則式（6）經傅里葉變換后如式（7）所示。

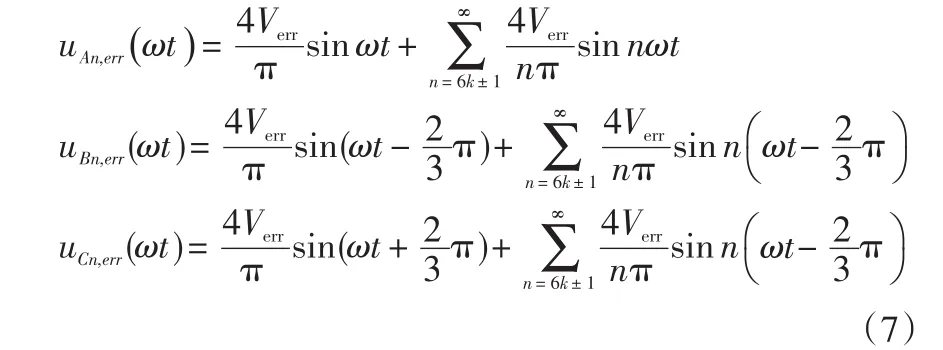
式中：k=1,2,3…；ω為電角速度值。

根據式（7）知，死區效應導致永磁同步電機三相誤差電壓波形中含有6k+1次諧波。由公式（3）可知，死區效應在輸出電壓中引入的擾動與死區時間成正比，與開關周期成反比。即死區時間越長，開關頻率越高，逆變器輸出基波電壓中的6k+1諧波就越多。同時，誤差電壓還與直流側電壓成正比，其矢量方向由電流極性決定。當電機在高速重載時，誤差電壓相對給定電壓較小，諧波成分較少，對控制系統的影響不大；但電機運行在低速輕載時，給定電壓減小，此時誤差電壓相比給定電壓無法忽略，電壓畸變嚴重，會使電機出現明顯的轉矩脈動和噪聲。

2 干擾觀測器構建

死區時間通常是固定的，但功率器件的開通和關斷延時、飽和導通壓降會隨著運行環境而變化，此外母線電壓的變化也會引起擾動電壓的波動。因此，干擾電壓是隨運行環境變化的時變值。針對擾動電壓存在的周期性波動以及環境變化帶來的不確定性影響，本文采用干擾觀測器（Disturbance observer，DOB）對死區效應引起的干擾電壓進行在線估計，并將觀測結果導入到指令電壓中進行補償。

三是機構間存在差別。依據機構特點、成果性質以及勞資合同或事先約定等情況的不同，各機構科研成果的收益分配情況不完全一樣。《雇員發明法》規定，高校雇員作為發明人應獲得發明轉化毛收入的30%，高校作為知識產權所有人獲得70%收入；如研發由兩個機構合作完成，則各獲35%，依此類推。但對高校外的獨立科研機構的收益分配沒有明確規定，在實際中是11%到30%之間。其中，主要從事前沿基礎研究的科研機構的發明人獲益較高，最多可得30%，如馬普學會[9～11]；主要從事應用研究的科研機構的發明人獲益較低，約為20%左右，如弗勞恩霍夫協會[7]。

在系統設計時，DOB能將系統不確定性造成的實際運行對象與名義模型輸出的差異視為系統擾動，并對擾動進行有效地估計和補償，實現對干擾的抑制[9-10]。DOB的控制結構如圖3所示，d為系統所受到的干擾；為干擾的估計值；GP(s)為實際運行對象的傳遞函數；ξ為系統觀測噪聲；Q(s)為低通濾波器，用以濾除測量噪聲。

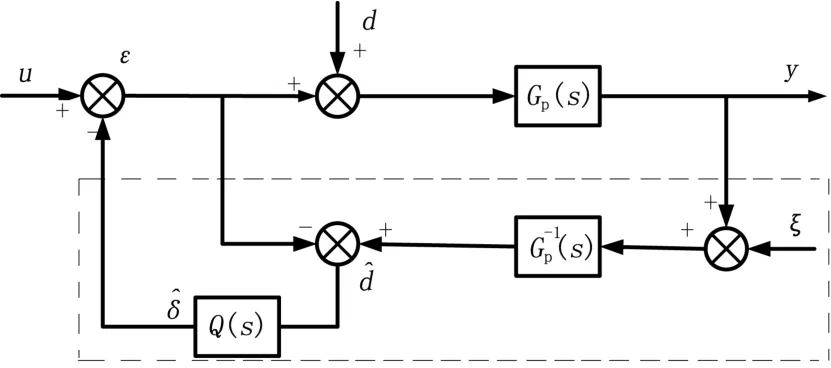
圖3 干擾觀測器結構圖

干擾觀測器估計結果中會含有大量觀測噪聲，而如果對逆變器三相輸出電壓信號直接進行觀測并濾波，會造成信號幅值的衰減和相位延遲，難以達到補償效果[11]。本文將死區效應、開關管動作延時等誤差電壓信號轉換到兩相旋轉坐標系中，實現誤差信號由矢量到標量的轉換。而對該信號的濾波不會造成相位延遲，并且可以直接前饋到控制器輸入端，簡化了實現方式。

考慮干擾電壓的永磁同步電機電壓方程在兩相旋轉坐標系下的表達如式（8）。

式中：Rs表示定子相電阻；Vd、Vq、id、iq、Ld、Ld分別為兩相旋轉坐標系下d軸和q軸電壓、電流、電感；ψf為轉子永磁體磁通；Vd,err、Vq,err為死區效應在旋轉坐標下的擾動電壓。

加入補償電壓Vd,com、Vq,com并對式（8）進行離散化后，PMSM電壓方程如式（9）。

根據式（8）和式（9），當前補償電壓Vd,com(k)，Vq,com(k)與干擾電壓Vd,err(k)，Vq,err(k)相等時，d軸和q軸電壓與PMSM理論值一致，消除了死區效應等干擾因素的影響。式（9）中采樣周期一般很小，在微秒級左右，因此可以認為在一個采樣周期內，干擾電壓的變化量接近于0。即

根據公式（10），可以利用前一個采樣周期的干擾電壓來估計當前周期的干擾電壓。即

圖4 在線死區補償原理圖

3 仿真驗證與結果分析

為了驗證對死區效應進行在線補償算法的有效性，本文通過MATLAB/Simulink建立系統仿真模型。首先搭建了針對永磁同步電機的速度-電流雙閉環控制模型，采用Id=0的磁場定向矢量控制和具有死區輸出的SVPWM算法。電機參數：極對數Pn=4，定子電阻R=0.958 Ω，定子直軸電感Ld=5.25 mH，定子交軸電感Lq=12 mH，轉子永磁體磁鏈ψf=0.182 7 Wb，轉子轉動慣量J=0.003 kg?cm2，SVPWM運行周期Ts=0.000 1 s，母線電壓311V。設定目標轉速為500 r/min，負載為10N·m。

圖5為無死區時間時，永磁同步電機三相相電流波形和坐標變換后dq軸電流波形圖。可以看出，在進入穩定段之后，電機三相相電流波形為標準的正弦波。dq軸電流波動很小。

圖5 無死區時的相電流波形

圖6為加入5 us死區后的相電流波形和頻譜。從圖中可以看出相電流有明顯的零電流鉗位現象，正弦度差，id波動明顯增大。從圖6（c）中可以看出，電流頻譜中含有較多的5th、7th、11th、13th諧波，符合式（7）分析中的6k+1次諧波擾動。此時相電流總諧波失真率為5.86%，電流畸變較為嚴重，死區對系統有明顯的影響。圖7為使用本文所提出的干擾觀測器在線補償后的相電流波形和頻譜。

圖6 5us死區的相電流波形和頻譜

如圖7所示，使用干擾觀測器進行在線死區補償后的相電流波形正弦度得到改善，零電流鉗位現象得到明顯抑制，d軸電流波動減弱，同時有效削弱了5th、7th、11th、13th等諧波，總諧波失真率由5.86%降至2.60%，有效降低了死區效應對整個系統的影響。

4 結束語

本文詳細分析了三相橋式電壓源型逆變器的死區效應，提出了基于干擾觀測器（DOB）的死區在線補償方法。該方法將死區效應、器件通斷延時等視作擾動電壓，進行在線估計并進行前饋補償，無需進行相電流極性判斷和參數離線測量便可實現對死區的有效補償。仿真結果表明，該策略可以有效抑制由逆變器死區帶來的零電流鉗位現象，減小電流諧波失真率，改善電流波形，提高系統的運行穩定性。

圖7 在線死區補償后的相電流波形和頻譜