非晶合金剪切帶動力學行為研究1)

董 杰 王雨田 胡 晶 孫保安*,*?,2) 汪衛華*,*? 白海洋*,*?,3)

*(中國科學院物理研究所,北京 100190)

?(中國科學院大學材料科學與光電技術學院,北京 100049)

**(北京工商大學材料與機械工程學院,北京 100048)

??(松山湖材料實驗室,廣東東莞 523808)

引言

剪切帶是一種材料塑性變形高度局域化的變形模式,廣泛存在于非晶體系的形變中,也是無序體系塑性形變的最主要載體,并對這些體系的失穩、災難性斷裂行為都有重要影響[1-4].常見的非晶體系如巖石、玻璃、聚合物、顆粒物和膠體等,或因為結構過于復雜,或因為力學性能較差,給剪切帶力學行為的實驗研究帶來了極大挑戰和困難.近年來,非晶合金這一新興玻璃材料的出現突破了這一困境,極大豐富了剪切帶的實驗研究,也激發了人們對剪切帶的研究興趣.于20 世紀60 年代,非晶合金是一種新型合金最先被發現[5],它可通過急冷熔融合金液體制得到.其最主要的特點是具有像玻璃一樣無序的原子結構,所以又被稱為金屬玻璃.結合玻璃結構和金屬鍵特性,非晶合金展現出許多優異的力學性能,如高強度和硬度、大彈性、耐磨耐蝕以及一定的塑性變形能力,在航空航天、精密機械、軍事武器等高技術領域展現出廣泛的應用前景[6-7].但也是因為其獨特的原子結構,非晶合金的力學行為與晶體合金迥然不同.受外力時,非晶合金的無序原子結構不能像晶格一樣通過位錯運動產生塑性形變,而是表現出多體相互作用的不穩定性,無序性和復雜性.

非晶合金的塑性形變具有強烈的溫度和應力依賴性[8].在接近或超過玻璃化轉變溫度Tg時,其塑性形變方式為均勻黏滯性變形,此時整體材料皆可參與形變.而在遠低于Tg的溫度下,其塑性形變表現出高度的空間局域化特征,材料塑性流動高度集中于厚度不超過20 nm 的剪切帶內.剪切帶內部應變量可以高達1000%～10000%[9],而其外部卻幾乎沒有塑性變形.在拉伸載荷下,剪切帶一旦生成就會在極短的時間內擴展失穩,導致非晶合金脆性斷裂而沒有拉伸塑性[10].這也極大限制了非晶合金作為結構材料應用于工程中.在受限加載(如壓縮、彎曲)條件下,由于正應力或幾何形狀等因素對剪切帶擴展和運動的限制作用,部分非晶合金可以通過剪切帶增殖和交互運動有效地耗散外界功,進而表現出一定的塑性變形[11-12].室溫下,剪切帶是非晶合金變形的最主要特征,與非晶合金的屈服,塑性和斷裂等力學行為是密切相關的,對非晶合金力學性能的設計、開發以及應用都至關重要.

除了空間上的高度不均勻性,非晶合金剪切帶運動還具有時間上的不連續性,表現為應力-應變曲線上的鋸齒流變行為[13-16].鋸齒流變行為通常出現在受限的加載條件下(如壓縮,彎曲和納米壓痕等),表現為在塑性變形階段,應力突然小幅下降,而后又彈性上升.應力上升部分為彈性加載的過程,這個過程中沒有塑性變形.而應力下降對應不連續的塑性變形事件,持續時間極短,通常在毫秒量級.應力升降循環交替出現,直到最后材料的斷裂.非晶合金的鋸齒流變行為反映了剪切帶運動的間歇性特點.

剪切帶這種在空間上的分布不均勻性和時間的運動不連續性,使其行為變成復雜的動力學系統.其主要表現為形貌和分布復雜無規律,運動和失穩具有災變性而難以預測,為相關研究帶來了極大的挑戰.但是近來研究發現剪切帶的行為也具有復雜動力學系統的特征,如自組織行為和混沌特征[17].這與自然界中一些典型的災變現象(地震,雪崩和山體滑坡等)以及物理體系中一些復雜系統的動力學行為(潤滑,磨擦,磁疇運動等)非常相似[18].因此,對非晶合金剪切帶行為的研究不僅對非晶合金的力學行為的認識和調控有重要意義,對自然災害的預防以及整個非晶體系形變行為的認識也有重要價值.本文結合團隊近年來在非晶合金剪切帶研究方面的結果,對非晶合金剪切帶力學行為和物理機制展開綜述,重點介紹其鋸齒流變和自組織臨界行為的表現,機制及與宏觀力學行為和性質的關聯,最后對非晶合金剪切帶的行為和性質亟需解決的問題以及未來的研究方向進行展望.

1 非晶合金間歇性塑性變形行為-鋸齒流變

1.1 鋸齒流變的實驗表象

非晶合金的剪切帶運動具有時間上的不連續特征,表現為應力-應變曲線上的鋸齒流變行為,如圖1 所示.應力上升部分為彈性的再加載過程;應力下降部分才代表材料的真正塑性應變過程,即剪切帶的形成和擴展過程鋸齒流變行為.在剪切帶形成和擴展之前,能量緩慢地進行積累,而一旦剪切帶形成之后便會迅速擴展,能量快速釋放.鋸齒應力下降幅度可用來表征鋸齒,因為應力下降幅度和材料的塑性變形密切相關,一般反映了剪切帶的滑移量的大小[19].隨著載荷增大,當局域材料屈服或剪切帶出現后,鋸齒流變行為便開始出現在力學響應中直到材料斷裂.不僅單一的塊體金屬玻璃材料會發生鋸齒流變,以塊體金屬玻璃為基體的復合材料也會形成鋸齒流變[20],而且在金屬玻璃的變形的分子動力學模擬中,也會觀察到這種現象[21],這說明鋸齒流變行為是金屬玻璃的一個普遍的力學響應.鋸齒流變行為也常見于自然界一些無序體系力學響應中,如地震波[22]、噪聲[23]和摩擦滑動[24]等,與無序體系的形變和失效機制密切相關.因此,研究鋸齒流變行為對認識金屬玻璃及其復合材料的變形機理具有重要意義.

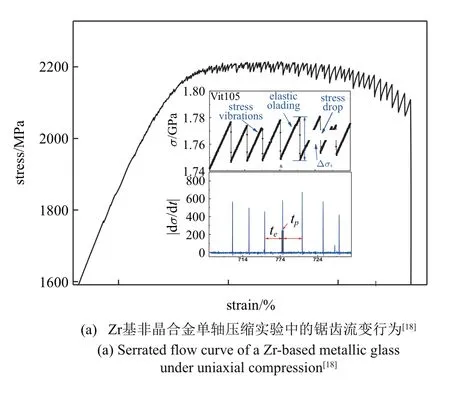
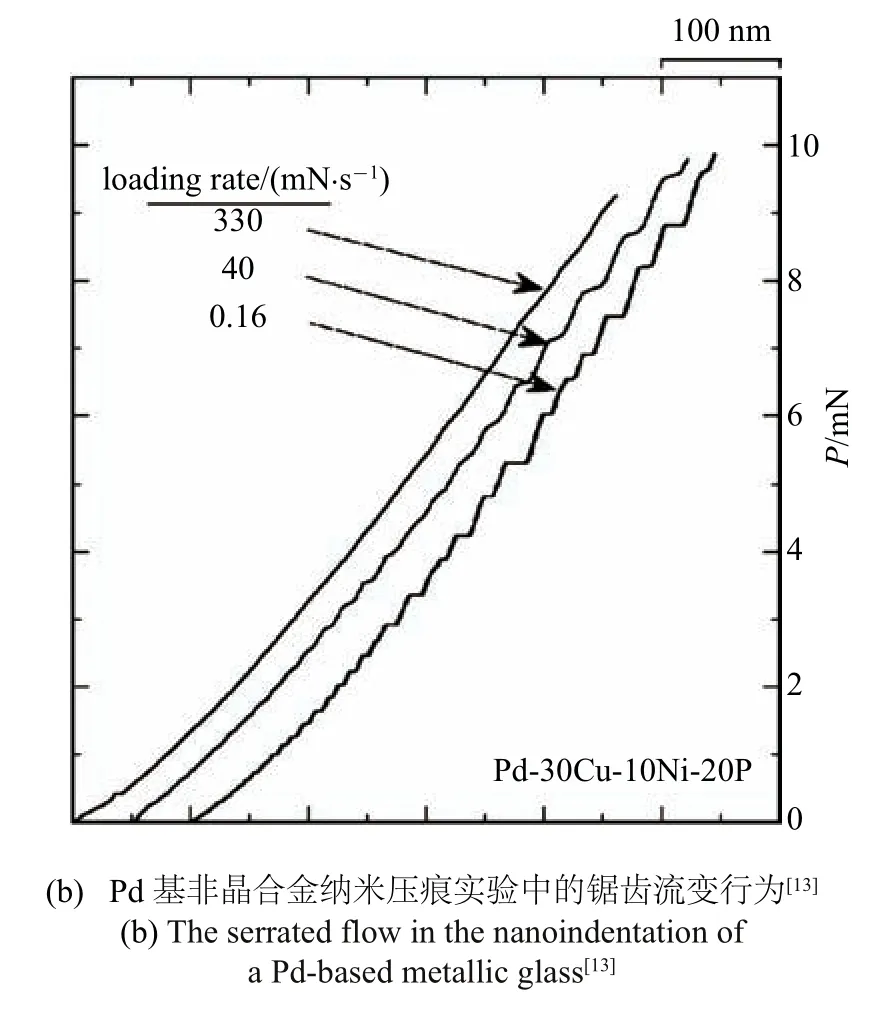
圖1 非晶合金的鋸齒流變行為Fig.1 The Serrated flow behavior of metallic glasses under mechanical tests

1.2 鋸齒流變的動力學特征

非晶合金鋸齒流變行為強烈依賴于其變形時的溫度和應變速率[17].隨著溫度的降低或者應變速率的增大,鋸齒流變行為會逐漸減弱.在某個臨界溫度或者應變速率,鋸齒流變行為將完全消失從而發生鋸齒向非鋸齒流變的轉變,說明鋸齒流變具有典型的動力學特征.本團隊分別在不同的溫度和不同應變率下對非晶合金的進行壓縮實驗,系統地研究了溫度和應變率對鋸齒流變行為的影響[16,27],以及鋸齒形貌和塑性形變的關聯性.發現在溫度低于某個臨界值或者應變率高于某一臨界值,鋸齒就會消失,如圖2 所示,同時塑性形變也大大增加.類似的現象在非晶納米壓痕實驗中也有報道.Schuh 和Nieh[13]在Pd 非晶納米壓痕中實驗中發現,應力鋸齒在一定的加載速率下會消失(見圖1(b)).通過系統的非晶合金壓縮實驗,發現其鋸齒流變行為和樣品的成分和彈性模量、形狀、尺寸以及測試儀器的剛度等各種內在和外在因素密切相關[28].當這些因素發生改變時,鋸齒的大小、間歇時間等特征也會發生明顯的改變,如圖3 所示.

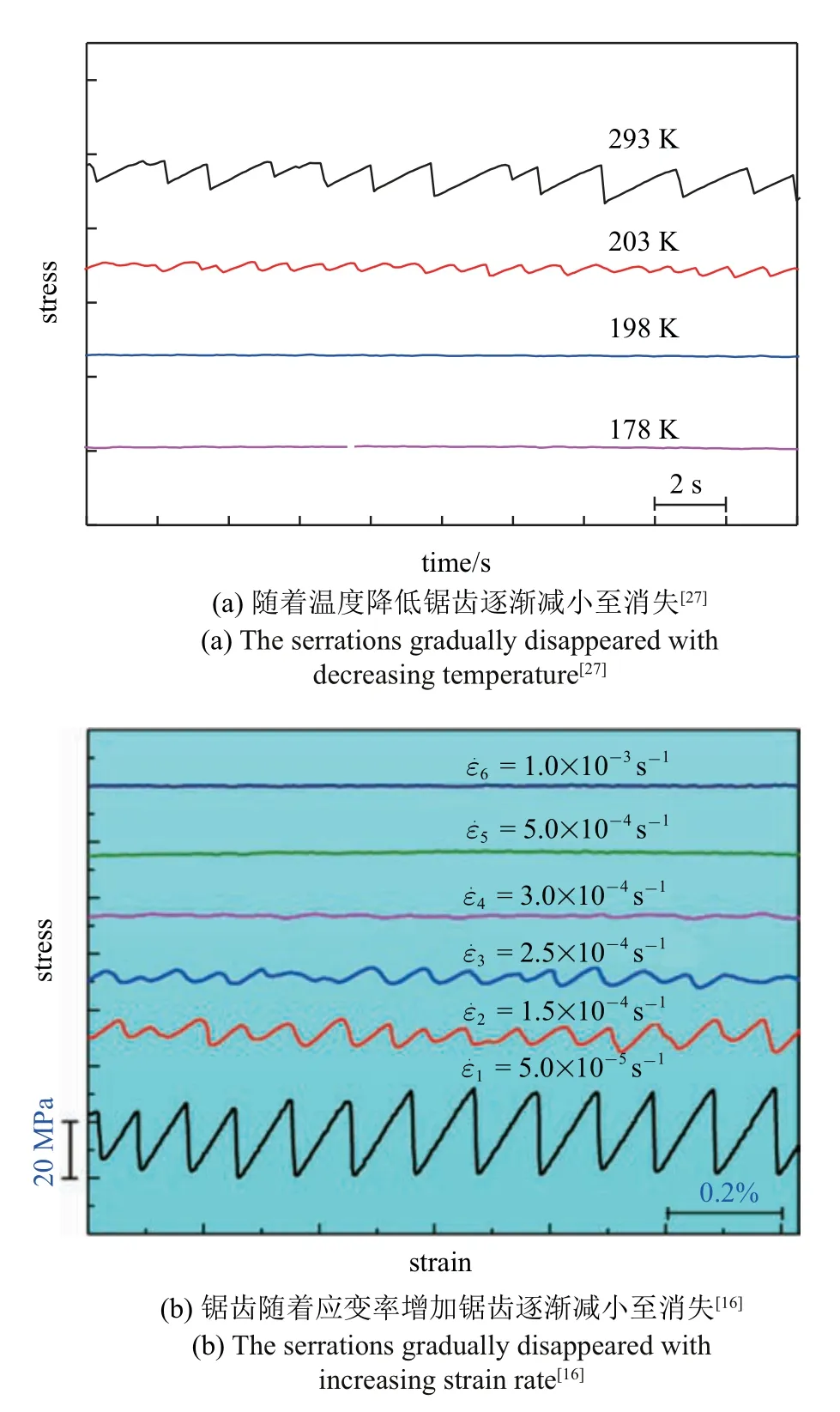
圖2 受壓縮時Zr 基非晶合金中的鋸齒流變行為和溫度、應變率的關系Fig.2 The temperature and strain rate dependence of serrated flow behavior for a Zr-based metallic glass under compression load

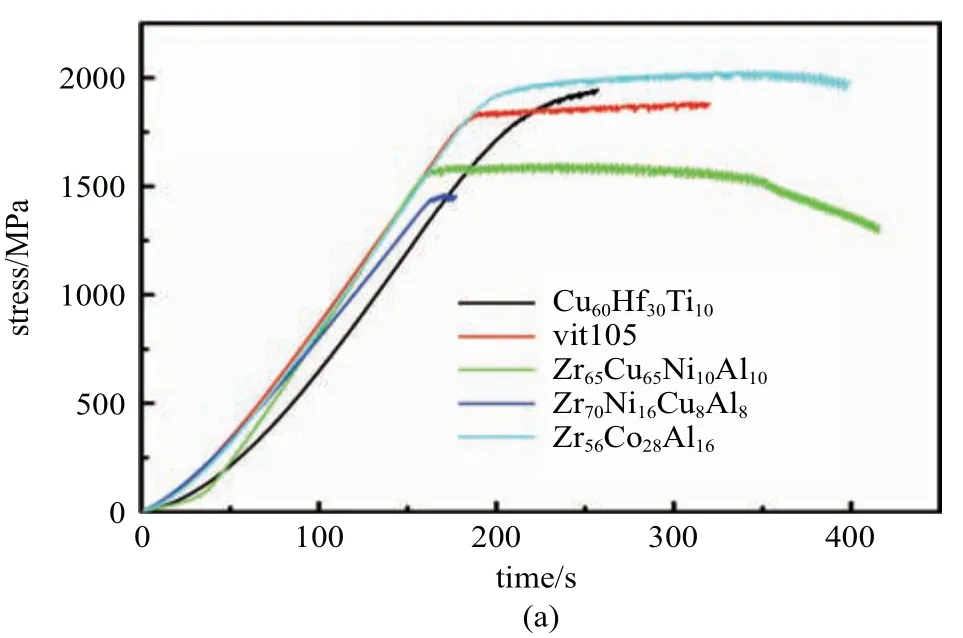
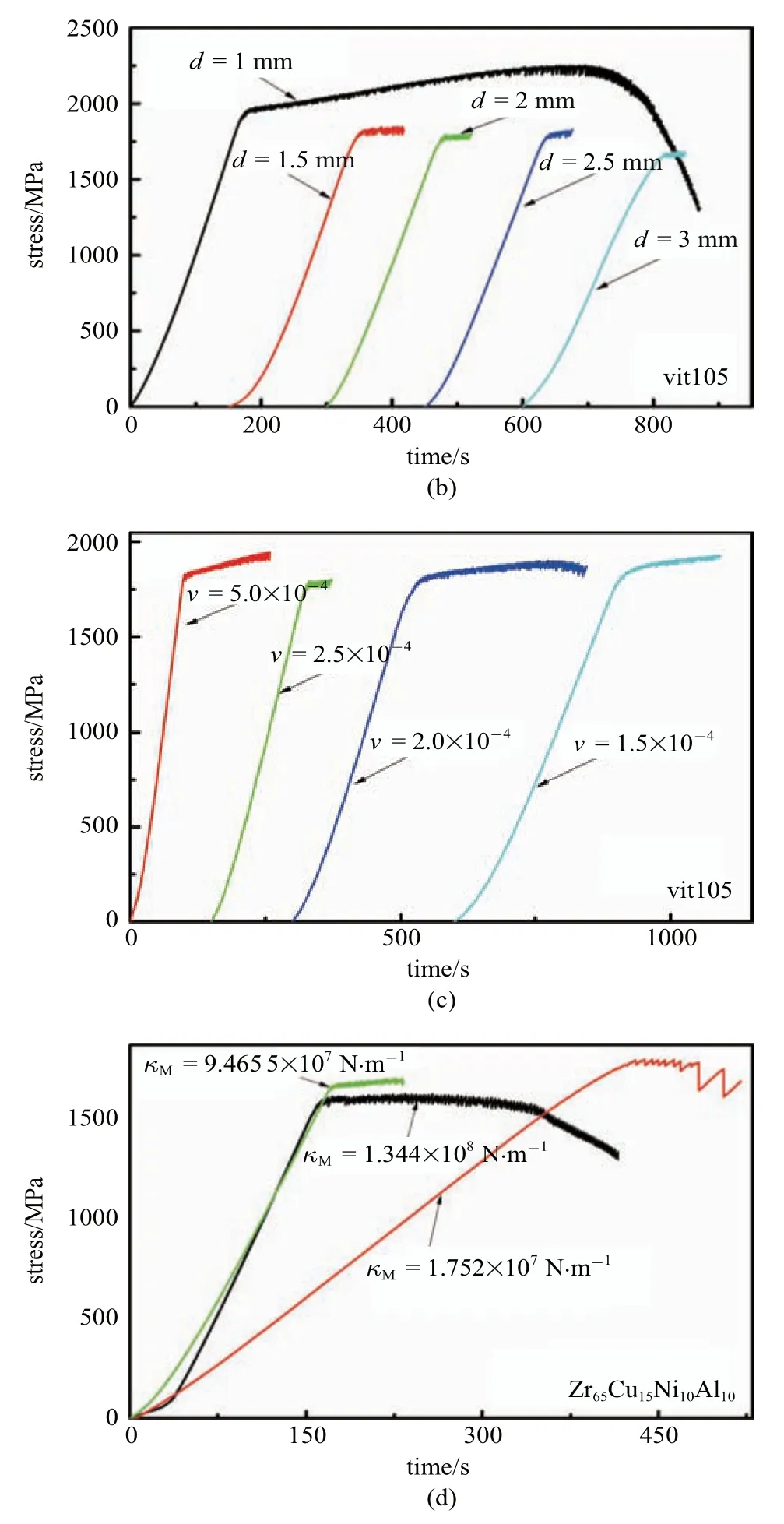
圖3 非晶合金在不同條下件受壓縮時的應力時間曲線[28]Fig.3 Typical stress-time curves for metallic glasses compressed under various conditions[28]

1.3 鋸齒流變在表征剪切帶性質中的作用

大量的實驗研究發現[25-29],除了極少數的韌性金屬玻璃外,大部分金屬玻璃的壓縮變形都可以形成一條主剪切帶,且這條主剪切帶在達到塑性屈服點時即可以貫穿整個樣品,隨后的變形過程以主剪切帶在整個滑移面的協同式的間歇性的滑移.這樣在塑性變形的穩定區域,應力應變曲線上的鋸齒和單個主剪切帶在滑移平面上的間歇性滑動具有一一對應的關系.通過對鋸齒流變過程中單個鋸齒的特征參數分析,可以研究剪切帶的動力學過程.利用應力鋸齒和剪切帶間歇性滑移的對應關系,可以間接地研究剪切帶的運動過程.Song 等[25]通過準確測量應力鋸齒降的持續時間和在鋸齒降過程中剪切帶的滑移距離,同時通過高精度的弓伸計可以精確測量剪切帶在鋸齒下降過程中的時間即剪切帶發生滑移的時間,計算出了剪切帶滑移過程中的平均速度,大約在300～800 μm/s 之間,如圖4 所示.并通過剪切帶速率可估算剪切帶黏度[25],如圖5(a)所示.

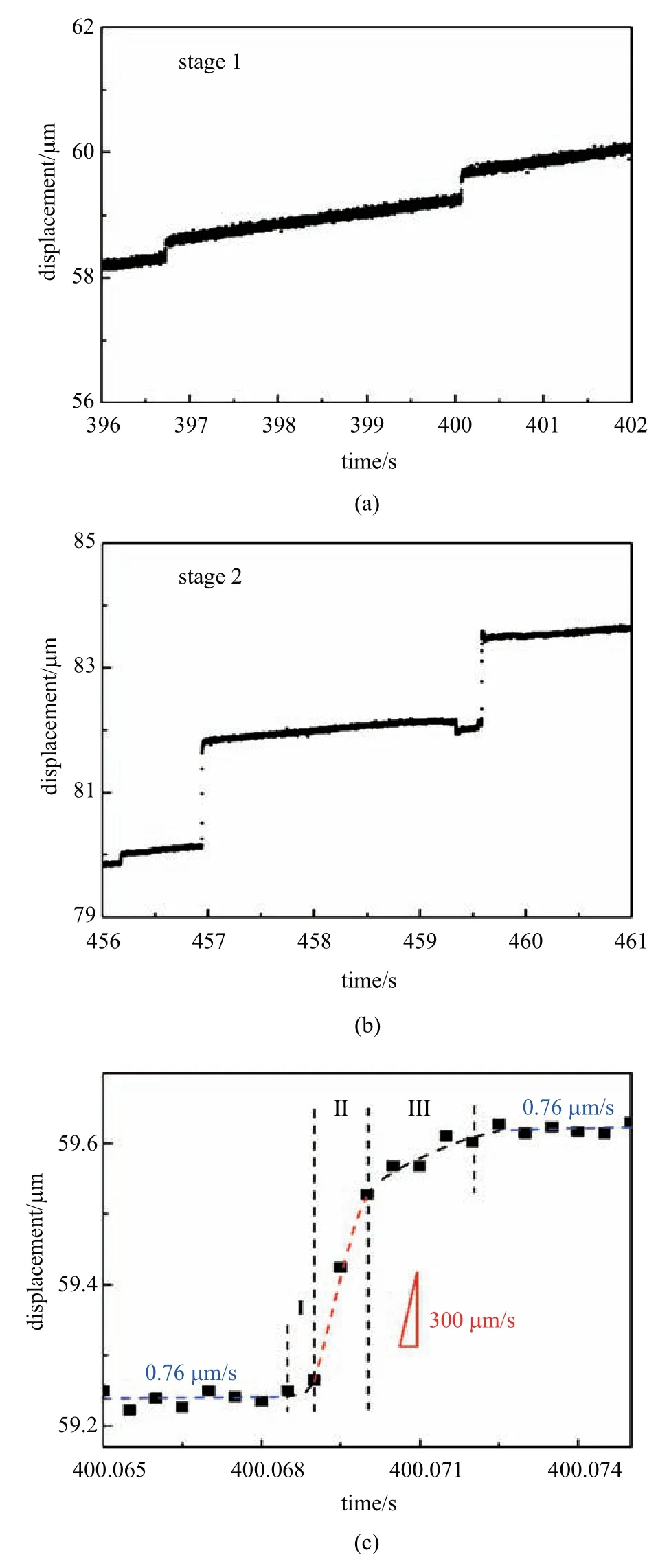
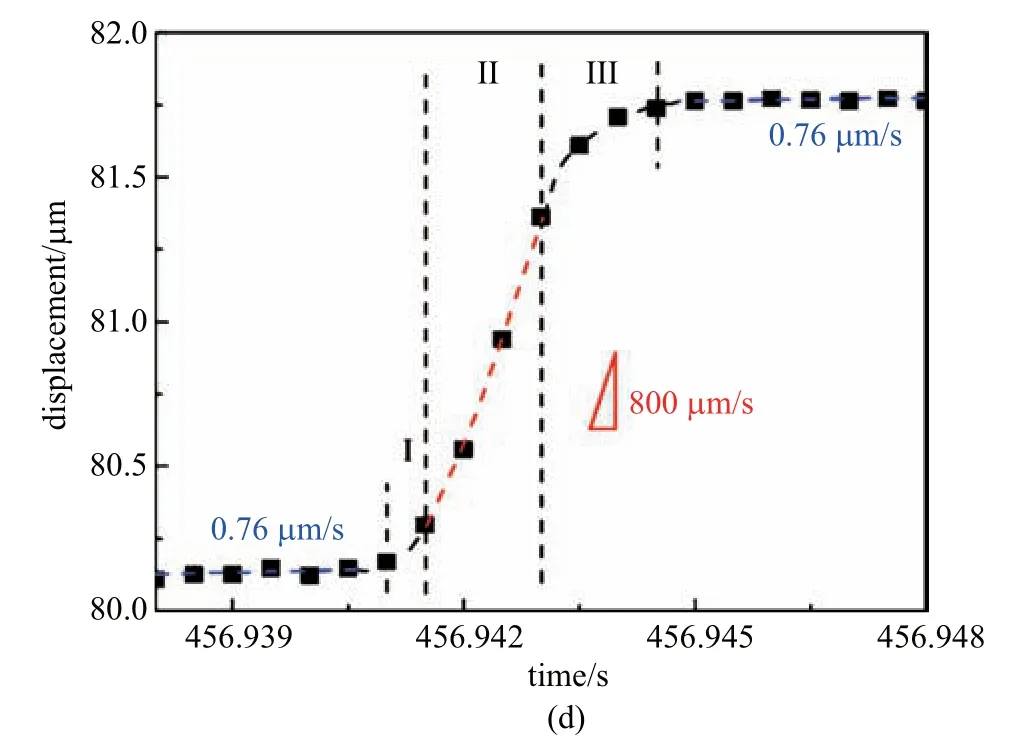
圖4 通過鋸齒行為計算剪切帶速率[25]Fig.4 Evaluate the sliding velocity of shear band through serrations[25]

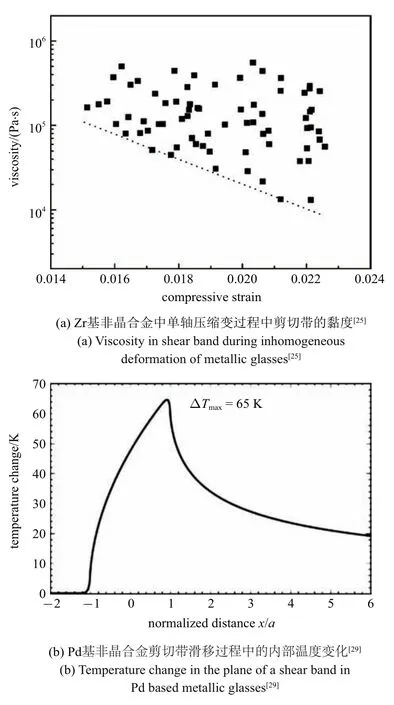
圖5 根據鋸齒信息計算的剪切帶內部黏度和溫度Fig.5 The evaluated viscosity and temperature in shear band through analysis of serrations

通過這種方法估算的剪切帶的黏度大約104Pa·s以上,已經達到過冷液體的黏度.Wright 等[29]則通過剪切帶速率根據熱傳導理論估算出其內部的溫升,如圖5(b)所示.計算溫升時考慮了兩種剪切帶的擴展方式,即剪切帶擴展前沿沿滑移面的擴展以及剪切帶在整個平面的協同滑移.發現兩種擴展方式下剪切帶的溫度最大升高僅為65 K.該溫度升高遠未達到該材料的玻璃轉變溫度.該結果證明了溫度升高可能在非晶合金的塑性變形過程中并不顯著.

1.4 鋸齒流變運動的物理機制

關于鋸齒流變的物理機制,目前普遍認為與剪切帶的形成和擴展密切相關.一種觀點認為鋸齒是剪切帶間歇式滑移運動的響應.剪切帶滑移時造成整個體系的部分彈性能釋放,導致應力突然下降.很多非晶合金在壓縮變形中通常只形成一條貫穿整個樣品的主剪切帶,并沿著主剪切帶滑移至最終斷裂.Song 等[15]用高速攝像機原位對壓縮過程剪切帶的變化進行了觀測,發現主剪切帶間歇滑移所形成的表面臺階和應力-應變曲線上的鋸齒具有一一對應的關系,而且在樣品的斷面觀測到了剪切帶滑移留下的規則的滑移條紋.該實驗有力地證實了鋸齒流變是剪切帶間歇性滑移的結果.另外一種觀點認為,一個鋸齒對應著一條剪切帶的形成和擴展的全過程,而應力曲線上循環出現的鋸齒是由于多條剪切帶不斷形成的結果.這種觀點主要基于非晶合金的納米壓痕現實驗,納米壓痕中壓頭下方材料所受應力比較復雜,通常形成復雜的多條剪切帶.Schuh 和Nieh[13]曾用這種觀點來解釋納米壓痕中的應力鋸齒在一定的加載速率下消失的現象.他們認為單個剪切帶的產生受動力學條件的限制,會存在一個臨界的最大產生速率,當外加應變速率超過該臨界速率時,多條剪切帶就會同時產生,導致較為均勻的塑性變形從而導致鋸齒消失.

2013 年,Sun 等[16]基于非晶合金壓縮實驗提出了一種剪切帶運動的stick-slip 模型,用以解釋鋸齒流變行為.該模型不僅考慮了剪切帶內部的本構變形行為,還包括了測試儀器的彈性變形對剪切帶運動行為的影響,如圖6 所示.在壓縮過程中,樣品和測試儀器可以看成是一個耦合的彈性系統,其剛度分別為kS和kM,彈性能存儲在樣品和測試儀器組成的系統中.材料一旦發生屈服,剪切帶新開始形成并滑移,造成整個系統的彈性能的突然釋放,從而導致加載應力的快速下降.在恒定的加載速率υ0下剪切帶滑移運動方程可表示為

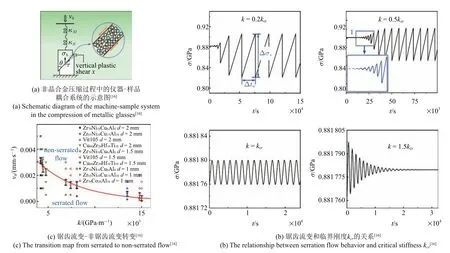
圖6 描述剪切帶運動的stick-slip 模型[16]Fig.6 The stick-slip model for shear band motions[16]

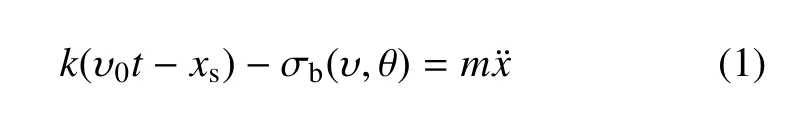
式中,k=E/[L(1+S)]為系統單位面積的彈性常數,E和L分別為樣品的彈性模量和高度,S=kS/kM;xs為剪切帶在t時刻的垂直滑移距離;m為系統的有效質量;σb(υ,θ)為剪切帶運動的垂直抵抗應力,一般為剪切帶滑移速度和內部狀態參量θ 的函數;σb(υ,θ)實際上代表了非晶材料流變的本構關系,可用STZ 理論來描述,這里采用了Johnson 提出的STZ理論表達式[32].采用有效無序溫度作為剪切帶運動演化的內部狀態參量,可以寫出其演化的動態方程.這樣就得到了描述單個剪切帶運動的完整的方程組.

對方程組數值解析發現,剪切帶的運動方程有一個穩態解.但在一定條件下,這種穩態解是動力學不穩定的,施加在該穩態解上的一些擾動會逐漸增大并最終發展成穩定的鋸齒,如圖6(b)所示.這說明鋸齒流變實際起源于剪切帶在運動過程中的一種本征動力學不穩定性.控制這種不穩定性出現的關鍵理論參數為kcr,稱為臨界剛度,可以表示為變形溫度和加載速率的函數

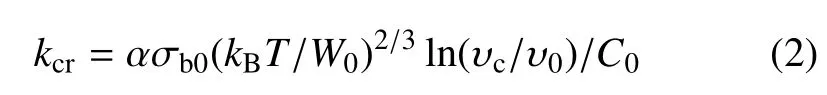
式中,α,C0為常數,σb0和υc均為剪切帶的特征強度和速度,W0為STZ 在0 K 的激活能.當k＜kcr時,剪切帶的運動是不穩定的,滑移過程中微小的擾動隨著時間而逐漸增大,最終發展成為穩定的鋸齒;在應力鋸齒的上升部分,剪切帶的滑移處于停滯(υ ?υ0),而在鋸齒的下降階段,剪切帶快速滑移(υ ?υ0);當k＞kcr時,鋸齒流變不會出現,剪切帶以外加載速度υ0穩態滑動;k=kcr對應鋸齒流變向非鋸齒流變轉變的臨界點.在鋸齒出現的范圍內,鋸齒的大小和k/kcr的比值密切相關:k/kcr越接近于1,應力鋸齒幅度越小.這個理論結果可以統一地解釋各種內在和外在因素對鋸齒流變行為的影響.從公式可以看出,鋸齒流變行為依賴于溫度和加載速率.在此可以用轉變圖來更直觀表示鋸齒流變對溫度和加載速率的依賴行為,如圖6(c)所示.當變形溫度降低或者應變速率增加時,kcr逐漸減小,而k不變,因此應力鋸齒幅度逐漸減小,當kcr降到k值以下時,鋸齒完全消失,鋸齒流變向非鋸齒流變的轉變.該理論預測結果和實驗結果符合得非常好.通過k=kcr,還可發現鋸齒消失的臨界應變速率符合Arrhenius 公式,即這也和實驗得到的擬合公式完全符合.樣品模量、大小和加載儀器剛度對鋸齒流變的影響都可以會反映在k值的變化上.例如,當樣品模量增高時,k值增大,k/kcr增大并接近于1,此時鋸齒逐漸減弱并最終消失;逐漸增加樣品的直徑(長徑比保持不變)或者測試儀器的剛度,也會產生相同的效果.通過進一步的理論分析表明,kcr和非晶合金流動強度的應變速率敏感系數相聯系,因此鋸齒流變出現的必要條件(kcr＞0)為非晶流動的負應變速率敏感系數.

從式(2)可以看出,實驗中測得的應力為σ=k(υ0t-xs),經過對時間微分變換可以得到剪切帶的瞬時滑移速度υs=υ0-(dσ/dt)/k.因此,如果采用高采樣頻率的載荷傳感器能準確地捕捉到鋸齒下降部分的應力隨時間的變化σ(t),就可以進行微分求導得到dσ/dt,從而利用上述公式計算得到剪切帶在鋸齒下降過程中的瞬時速度變化.采用上述方法,對非晶合金從屈服到最后斷裂發生之前的主剪切帶的瞬時速度變化進行了追蹤,并提取出剪切帶失穩的臨界最大速度.通過對各種不同條件下90 個非晶合金樣品的測量,發現剪切帶失穩的臨界速度趨于一個常數(約為1.5×10-4ms-1).該實驗說明剪切帶的失穩過程受一個臨界應變速率的控制,這也正好驗證了Furukawa 和Tanaka 提出的剪切帶失穩的液體不穩定性理論,這也從側面說明了非晶合金的剪切帶變形過程是一種由應力弓起的玻璃轉變現象.

2 剪切帶運動的復雜動力學行為

自組織臨界性(self-organized criticality,SOC)是20 世紀80 年代由物理學家Bak 等提出來描述復雜非平衡態系統時空演化規律的重要理論[30].復雜系統和現象廣泛存在于自然界、物理、生物以及社會科學中,與人們的生活密切相關.通過大量數據的研究和分析,人們逐漸注意到其中的一些現象,如地震和森林火災等災難事件的發生、電子器件的噪聲、心率的漲落、DNA 序列、股票價格變化、高速公路車流的變化等,雖然表面表現出復雜和隨機性且內在物理機制不同,但在動力學行為演化上卻表現出相似的簡單規律[31].所謂的臨界性,是指系統的動力學行為在時間上和空間上均沒有特征尺度,即符合冪律分布.如從同一地區長時期發生的地震規律來看,大地震并不常見而小震時有發生.一條河流其主流并不多而支流分岔較多.地震的震級和其發生概率、河流的大小和數量之間均符合冪律分布.時間上的冪律分布即閃爍噪聲效應;空間上的冪律分布則為分形的幾何結構.

經典的沙堆模型可很好地描述自組織臨界狀態的形成[31].在一個平臺上逐漸加沙粒來形成一個沙堆,每次加一粒.隨著沙堆的升高,其斜度也逐漸增大.但沙堆斜度不能無限增大,當達到一定斜度后就不再變化.此時的沙堆系統便演化到了一個臨界狀態,每加一粒沙子就會弓起沙堆的坍塌.沙堆的坍塌在時間或空間上沒有特征尺度,除了受其自身尺寸的限制外,任何大小的沙堆坍塌都可能出現,它們的發生滿足冪律分布.沙堆之間的沙粒雖然只有短程的局域相互作用,卻可以弓起系統內部的長程相互作用關聯.此時的沙堆便處于自組織臨界狀態.

室溫下金屬玻璃的塑性變形主要是通過大量剪切帶的運動實現的.這些剪切帶的運動在力學響應上表現為間歇性鋸齒流變行為,本質上是一種典型的復雜動力學現象.2010 年團隊從復雜動力學演化方面對非晶合金的鋸齒流變行為展開研究,發現韌性非晶合金的剪切帶運動可演化到自組織臨界狀態[17].通過分析8 種不同成分和塑性能力的塊體非晶合金的單軸壓縮的應力-應變曲線,發現韌性非晶合金(塑性應變在εp＞10%)和脆性非晶合金(εp＜5%)的鋸齒特征明顯不同,如圖7 所示(以Vit 105 和Cu47.5Zr47.5Al5塊體非晶合金為例).對鋸齒應力降幅的統計分析可以發現,脆性非晶合金的鋸齒降幅的柱狀分布圖接近高斯分布,如圖7(b)所示,說明這些合金的鋸齒有一個特征尺度大小;而韌性非晶合金的鋸齒柱狀分布則呈單調下降的趨勢,如圖7(b)所示.通過計算概率密度分布函數D(s)=(1/N)·(δN(s)/δs)對鋸齒降幅分布進一步定量分析后,可以發現韌性非晶合金的概率密度分布函數很好地符合冪律分布:D(s)～sα,如圖8 所示.其中N為降幅的總體數量,s為約化后的鋸齒降幅,α 為冪指數.統計分析發現4種韌性非晶合金均表現出冪律分布規律,其擬合的α值在1.3～1.5 之間.

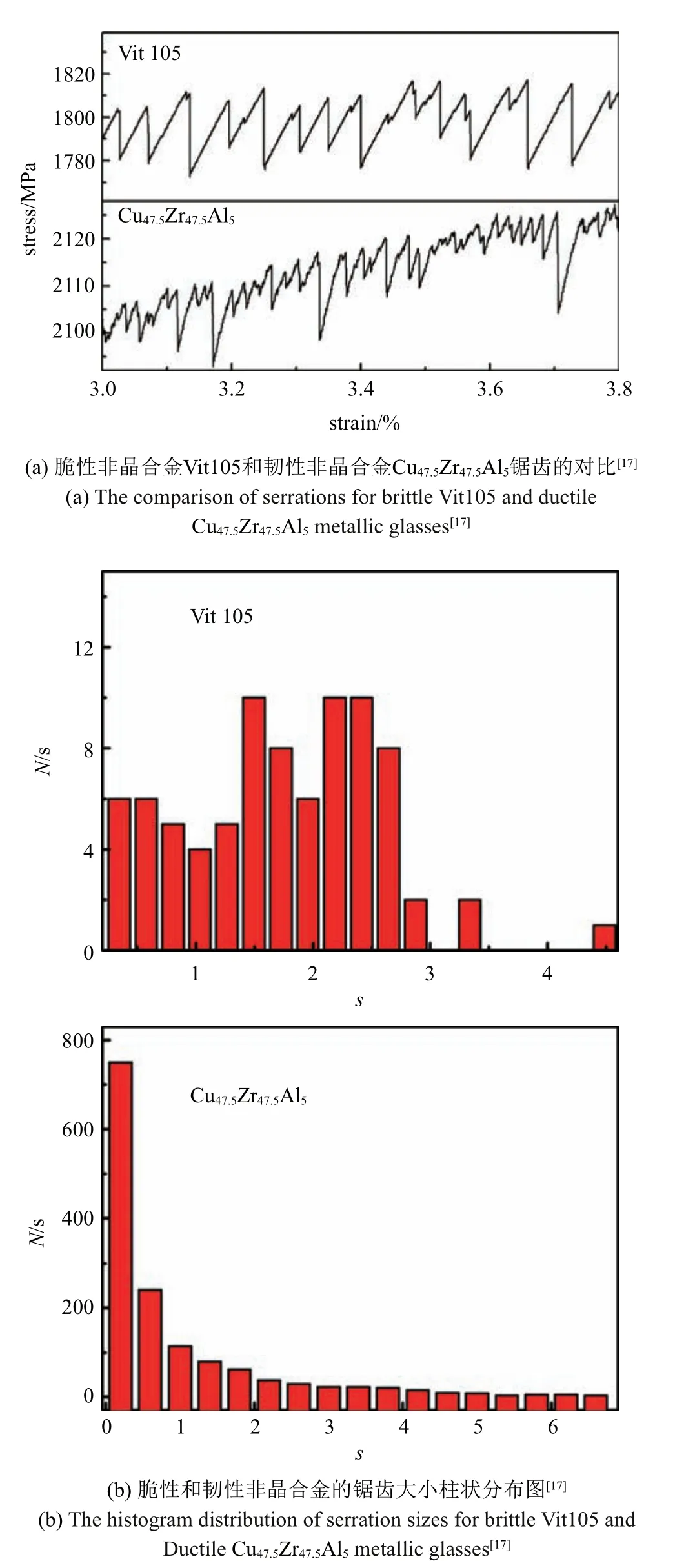
圖7 脆性非晶合金Vit105 和韌性非晶合金Cu47.5Zr47.5Al5鋸齒行為的對比[17]Fig.7 The comparison of the serration behaviors between brittle and ductile metallic glasses[17]

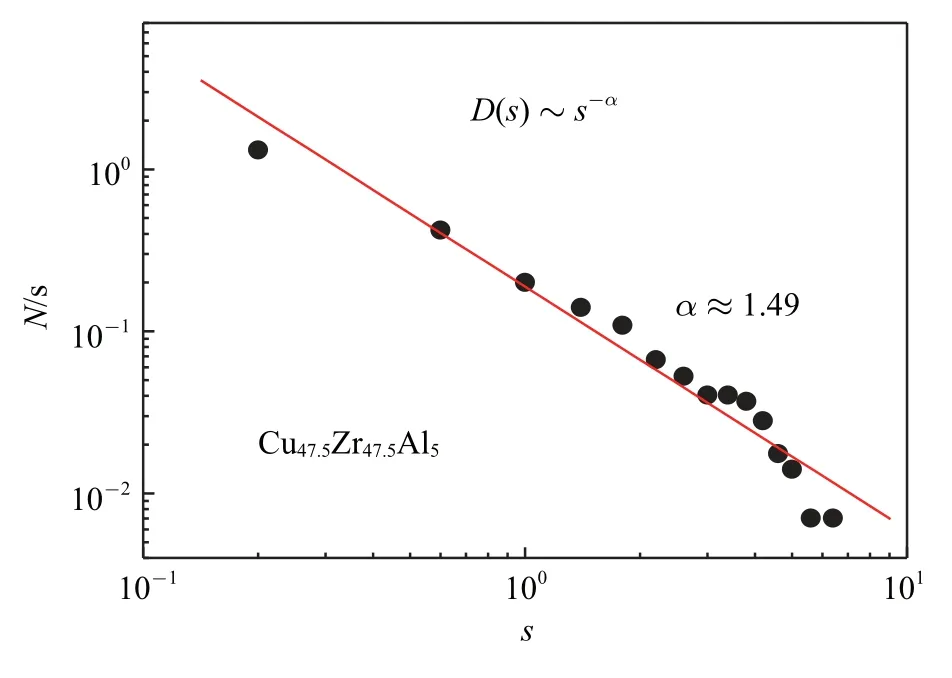
圖8 Cu47.5Zr47.5Al5非晶合金鋸齒應力降幅的概率密度分布函數D(s)[17]Fig.8 The density distribution D(s)the Cu47.5Zr47.5Al5metallic glass[17]

非晶合金的塑性變形可以看成一個動力學過程,每次鋸齒下降可看作是單獨的動力學事件,這些事件的冪律分布證明韌性金屬玻璃的塑性變形實際上是處于自組織臨界狀態.每個鋸齒應力的下降對應于剪切帶的形成和擴展過程,其降幅和剪切帶的滑移距離成正比,因此鋸齒事件的冪律分布也說明剪切的運動的自組織臨界性.對另外4 種脆性非晶合金的高斯分布的鋸齒進行時間序列分析發現,其鋸齒動力學具有混沌的特征,表現為正的李雅譜諾夫譜和一定范圍內恒定的相關作用維數[33].脆性金屬玻璃的塑性變形通過主剪切帶滑移運動進行,如圖9(a)所示,此過程中主剪切帶中的應變、應力、溫度及自由體積都會隨著時間變化,這些變量相互影響可能會使其動力學行為演化到混沌狀態.而韌性金屬玻璃的在受限載荷能夠產生多重剪切帶,如圖9(b)所示,剪切帶之間交互、阻礙及分枝所形成的剪切帶網能夠有效耗散外界功和減緩應力集中,產生交大的塑性變形.

圖9 金屬玻璃壓縮變形后的剪切帶形貌[18]Fig.9 The patterns of shear bands in metallic glasses after compression deformation[18]

在非晶變形過程中所產生的剪切帶之間存在著復雜的相互作用,對塑性變形以及自組織臨界狀態的形成有重要作用.一條剪切帶的滑移會弓起非晶內部應力的重新分布,從而對其他剪切帶的運動行為產生影響.但由于剪切帶產生的隨機性和“二維”特性,從理論分析上直接求解剪切帶之間的相互作用非常困難.由此Sun 等[17]提出了一個簡單的多重剪切帶滯滑運動模型,可很好描述和解釋研究剪切帶相互作用對其運動擴展行為的影響.在該模型中,每個剪切塊都可以在單獨的彈簧加載下發生滯滑運動,且只形成一個剪切帶.剪切塊之間通過耦合彈簧相連,這樣每個剪切塊滑移都只會對其鄰近的剪切帶的行為產生影響,即只有剪切帶的短程的的彈性相互作用.彈簧的勁度為k,耦合彈簧的勁度為kc,加載彈簧在恒定的速率下加載,速度為v0,每個剪切帶的垂直滑移位移為xi.剪切帶的運動方程可寫為

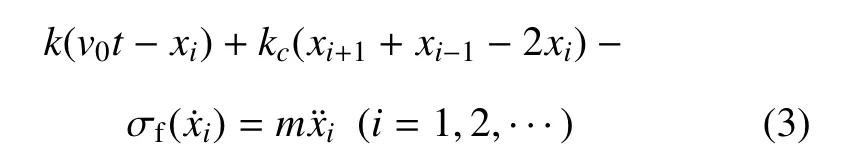
其中左邊第1 項代表加載應力,第2 項代表近鄰剪切帶之間的相互作用力,N為剪切帶的數目.為剪切帶的內在抵抗力,取決于和樣品成分,剪切帶滑移速度和溫度.對方程組的數值求解,可發現剪切帶運動受相互作用影響在時間和空間上具有協同性,并組織成一系列不同大小的間歇性出現塑性變形事件,如圖10 所示.對這些鋸齒事件進行統計分析發現,其出現的概率符合標準的冪律分布,冪指數為1.42,與實驗得到的冪律指數接近.

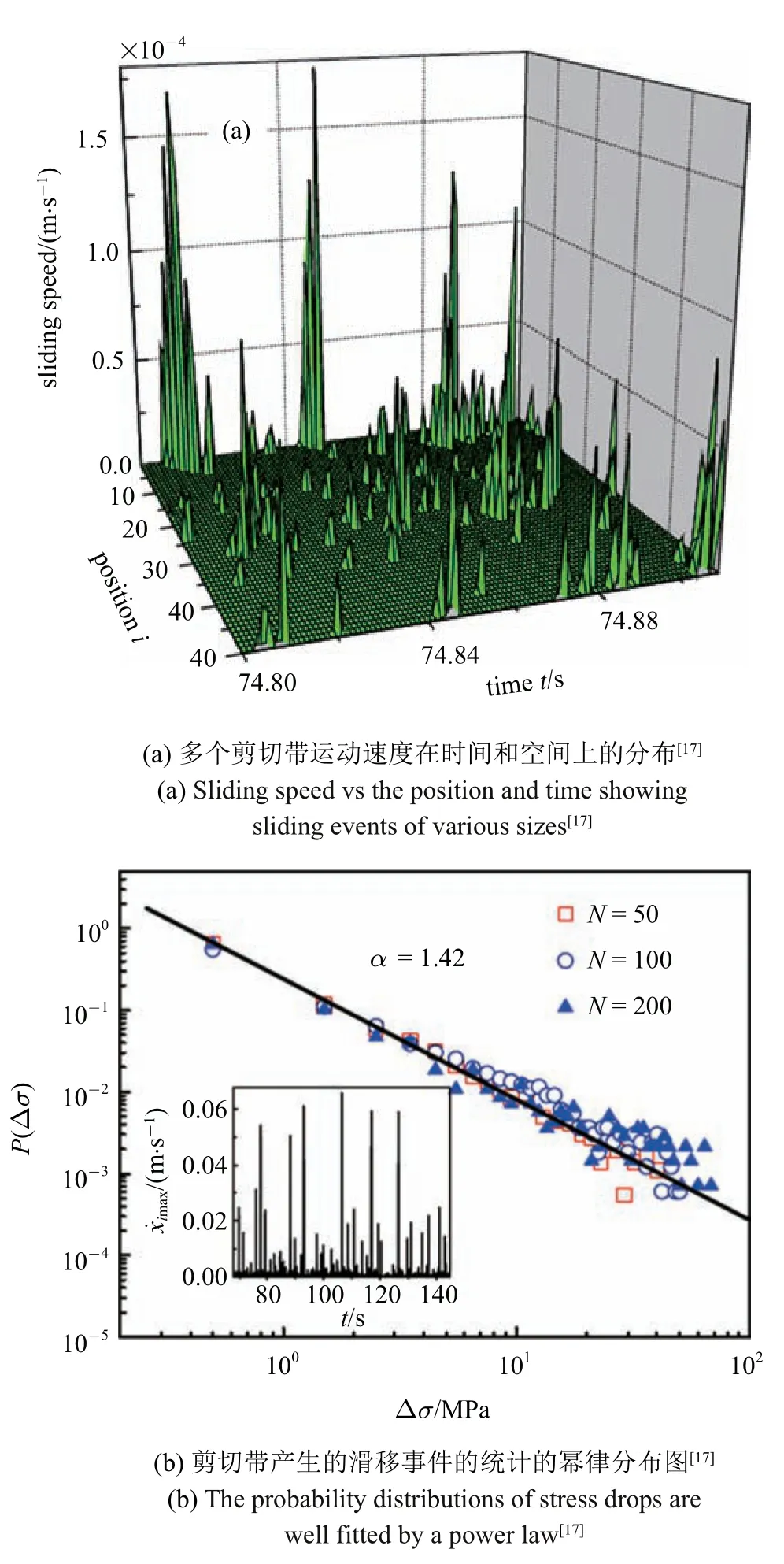
圖10 多重剪切帶相互運動產生的自組織臨界性的理論計算結果[17]Fig.10 Numerical solutions for the stick-slip model of multiple shear bands[17]

實驗上可通過對多個非晶樣品同時壓縮,直接觀測剪切帶之間的相互作用對鋸齒動力學行為的影響.壓縮時每個樣品都會形成一條主剪切帶,而剪切帶之間的彈性相互作用通過加載的儀器傳遞.實驗發現,在弓入剪切帶相互作用后,應力-應變曲線上的鋸齒行為變得更加復雜.鋸齒的統計分析結果和理論數值計算結果符合得很好.這進一步說明剪切帶之間的相互作用對韌性非晶合金的自組織臨界狀態的形成具有重要的作用.剪切帶自組織形成的這些標度不變的鋸齒事件和地震的發生在運動物理方程和表現形式上都具有相似性,因此韌性非晶合金的剪切帶運動可以作為模擬地震發生的一個理想的實驗體系.

3 剪切帶的復雜空間形貌特征

對于自組織臨界狀態的動力學系統,其動力學事件在時間上表現為冪律分布,而在空間上則呈現出具有自相似性的分形結構.分形(fractal)是非整數維形式充填空間的一種幾何特征,通常被定義為“一個粗糙或零碎的幾何形狀,可以被離散化,且每一部分都(至少近似地)是整體縮小后的形狀”.美籍數學家本華·曼德博(法語:Benoit B.Mandelbrot)于1975年首先提出分形(fractal)的概念[33],其原意具有不規則、支離破碎等意義.從整體上看,具有分形特征幾何圖形是處處不規則的,但是在不同尺度上,圖形的規則性又是相似的,即自相似性[34].典型分形結構如閃電,山川和海岸線的形貌,從遠距離觀測其形狀極不規則,但從近距離觀察,其局部形狀又和整體形態相似.分形最重要的特征就是它的分數維,對于一個線性大小為L的幾何結構,如果其體積V(L)滿足V(L)=LD,則此結構可以看作具有分形特征,D為分形的維數,也被稱為Hausdorff維數,D一般大于分形所嵌入的空間維數.在實際應用中,由于分形結構的形貌復雜,其體積V(L)很難被精確地測定,所以一般用其他方法來測定分形的維數.其中比較常見的方法有盒子計數法(counting boxes)和空隙分布統計法(hole distribution)[35].

韌性金屬玻璃在發生大塑性應變時所產生的多重剪切帶,如圖11(a)所示,分布不均勻且圖案比較復雜,Sun 等[36]通過盒子計數法(Box-Counting)和空隙分布統計法(hole distribution)對這些剪切帶的分布進行了統計分析,發現這些多重剪帶具有分形結構的特征,其分形維數在1.5～1.6 之間.盒子計數法即用邊長為Δx的小正方形去覆蓋剪切帶圖案(剪切帶圖像被預先數字化為二進制黑白圖,一條剪切帶的至少一個像素點被包括),然后統計這些小正方形的數目N(Δx).對圖中的剪切帶分布進行統計分析后發現,N(Δx)和Δx之間關系表現出典型的分形特征如圖11(b)所示,,其中盒子維數DB=1.53.進一步用空隙分布統計法對圖11(a)中剪切帶間的空隙分布進行了統計分析,發現分形之間的空隙分布也很好地符合分形結構特征N(λ ＞Λ)=CΛDG,其中分形維數DG=1.62,Λ 為空隙的線性大小,N(λ ＞Λ)為線性大小超過Λ 的空隙的個數,C為常數,取決于該空隙的形狀,分形結構的總面積A及指數DG.DG與盒子統計法中的DB接近,進一步證明剪切帶的分布形貌確實具有分形特征.

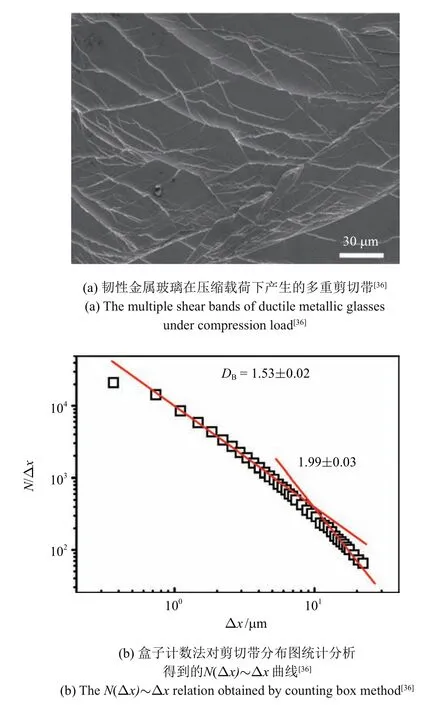
圖11 韌性金屬玻璃的具有分形特征的剪切帶圖貌[36]Fig.11 The fractural morphology of shear bands[36]

隨著金屬玻璃的變形的進行,剪切帶相互交織形成分形結構,在此過程中剪切帶交互時的相互作用必定起了重要作用.剪切帶群形貌復雜,且包含剪切數量極多,因此直接計算剪切帶之間的相互作用極其困難.我們通過一種簡單而有效的模型分析了剪切帶的相互作用在分形結構的形成過程中的影響.一條正常擴展的剪切帶,除了受到一個來自外加載荷的切應力τext,還受到一個由剪切帶之間的相互作用弓起的瞬時切應力τint,該剪切帶受到的有效切應力可表示為τeff=τext+τint.這個瞬時切應力是隨時間變化的,可以看作為疊加在外加切應力上的噪聲,對剪切帶的應變速率的有微小擾動作用.對于均勻變形中的金屬玻璃,局部剪切應變率可以表示為其中為特征應變速率,ΔG為剪切帶應變的激活能,Vap為該局部區域的激活體積,kB為玻耳茲曼常數,T為溫度.根據Furutsu–Novikov 理論,將剪切帶運動類似于位錯滑移,則可得到準靜態平衡狀態下的瞬時切應力,其中〈·〉 是對時間取平均值,S=?ln〈τeff〉/?ln〈〉 為應變率敏感因子.可見,瞬時切應力τint并不是完全隨機的白噪聲.一般來說τint是應變率γ,應變率敏感因子和隨機噪聲δw的函數金屬玻璃的應變率敏感因子通常都很小,在此可被忽略.假設τint只是應變率和隨機噪聲的線性函數:τint=Aγ+Bδw.其中A和B為比重因子.把τint代入局部剪切應變率方程,進行泰勒展開并保留線性項可得

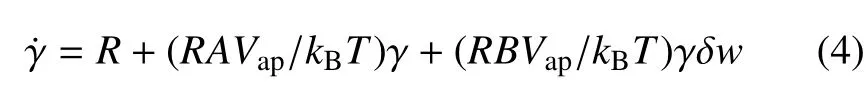
式中,是穩態應力弓起的恒定應變率.式(4)是典型的Langevin 公式,通過求解其對應的Fokker–Planke 公式可得穩態應變率γ 的概率分布函數

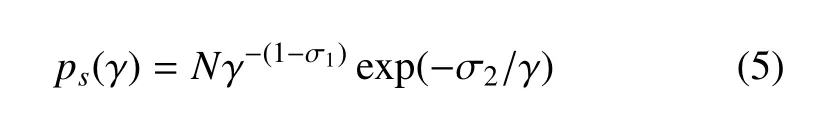
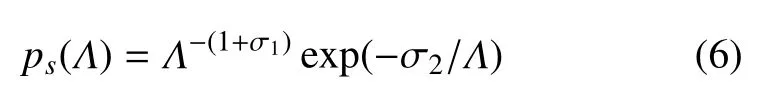
σ1,σ2,取不同值時的ps(Λ)的形狀如圖12(b)所示,可以看出隨著剪切帶間距的增大,ps(Λ)呈單調下降的趨勢.當Λ →0 時,有ps(Λ)=Λ-(1+σ1),此時累積概率分布函數N(λ ＞Λ)～Λ-σ1,表現出典型的分形特征,其分形維數為σ1,同時也證明剪切帶群是一種分形結構.根據σ1的表達式,其大小與比重因子A,B的值相關,即與剪切帶相互作用力大小密切相關,進一步說明剪切帶之間的相互作用在剪切帶分形結構的形成中起了非常重要的作用.

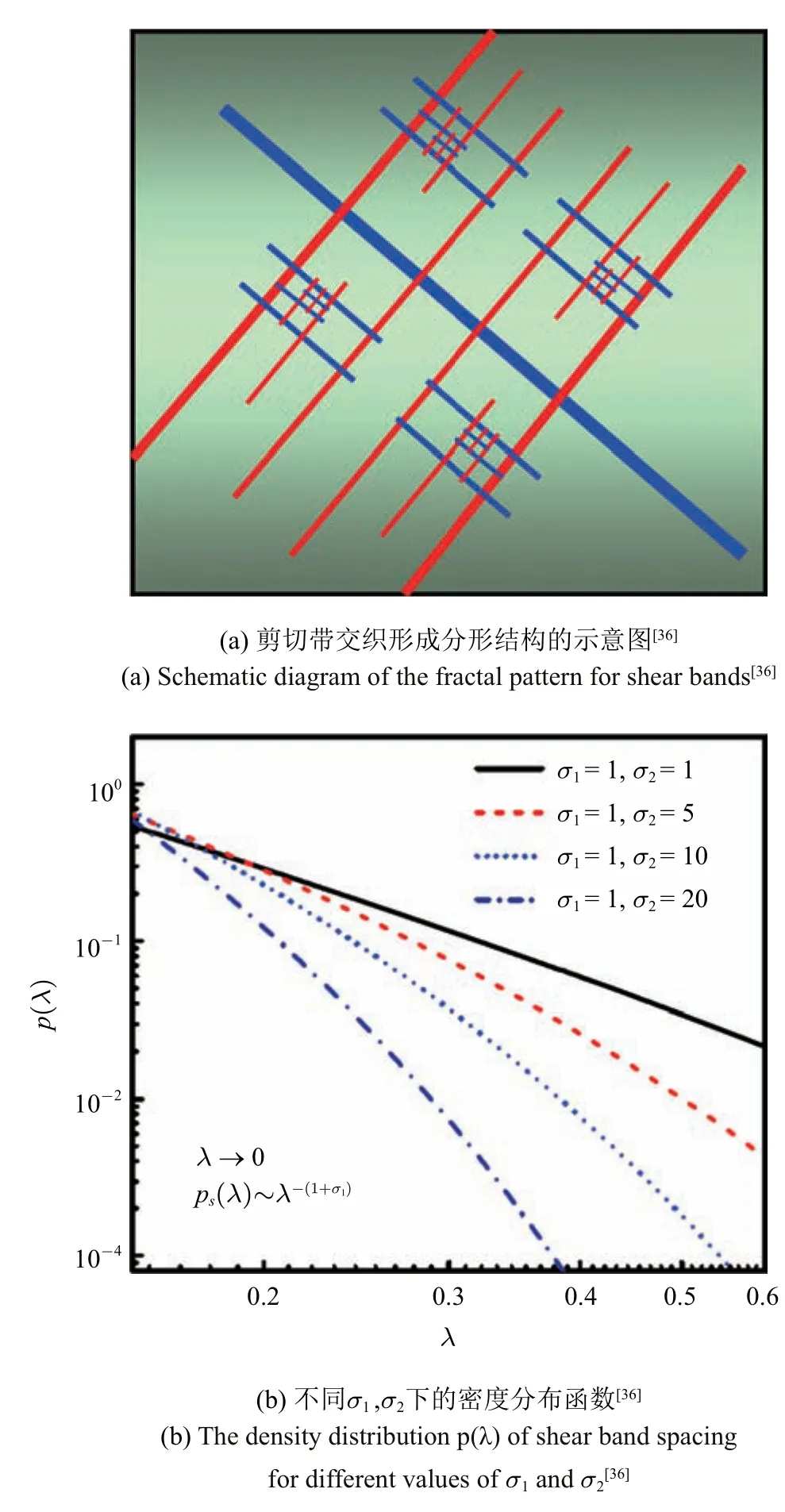
圖12 多重剪切帶形成的模型[36]Fig.12 The model for shear bands formation

4 結論

綜上所述,非晶合金剪切帶具有高度時空不均勻性,是一種高度局域化的塑性變形.其運動具有時間上的不連續特征,表現出間歇性鋸齒流變行為.鋸齒流變行為起源于剪切帶的滯滑運動,是剪切帶在運動過程中的一種本征的動力學不穩定性.鋸齒流變行為對剪切帶的研究具有重要價值,通過鋸齒流變行為可以間接地探索剪切帶的運動,剪切帶運動和外加條件的耦合聯系以及剪切帶的內在性質.剪切帶之間存在復雜的相互作用,使其整體表現有自組織臨界行為,形貌具有分形特征,和自然界很多復雜的動力學系統行為相似.

經過科研人員幾十年的努力,雖然在非晶合金的剪切帶運動在理論和實驗研究上取得了很大的進步,但仍許多問題需要研究:(1)非晶合金鋸齒流變過程中剪切帶的動態性質如速度、溫度如何演化以及失穩的問題,該問題對理解非晶合金的塑性和斷裂非常重要;(2)各種因素對非晶合金剪切帶自組織臨界行為影響的具體機制以及自組織臨界行為向混沌行為轉變的問題;(3)剪切帶的內部結構,性質及其起源的微觀機制;這些問題的解決將有助于建立統一非晶合金剪切帶運動理論,對高性能非晶合金的設計和開發也有重要的指導意義.