六自由度液壓換刀機械臂的設計與分析

孫顏明，徐莉萍，任德志

1河南科技大學機電工程學院 河南洛陽 471003

2鄭州科技學院機械工程學院 河南鄭州 450064

在 盾構機施工過程中，刀具的磨損不可避免。當刀具磨損到一定程度時，便需要對刀具進行更換，否則會損壞盾構機的刀盤，影響盾構機的正常掘進，甚至會縮短盾構機的壽命。根據調查發現，目前盾構機換刀采用的人工更換方案，不僅耗資大、耗時長，且嚴重危害作業人員的健康[1]。國外通過對KUKA 機械臂進行改造，用于盾構機刀具的拆卸與安裝[2]，但由于該機械臂本體結構的局限性，導致其不能很好地適應盾構機內部環境。

筆者根據盾構機內部結構，以及液壓技術的發展，設計了一款盾構機專用的液壓驅動換刀機械臂，以降低盾構機換刀的成本，提高換刀效率與總體施工效率，保證整個隧道施工過程的順利進行。通過對換刀機械臂進行運動學分析和軌跡規劃研究，為其運動規劃、智能控制等研究提供依據。

1 換刀機械臂本體設計

1.1 技術難點分析

通過對現有人工進倉換刀方案進行分析，結合盾構機的結構環境，確定換刀機械臂的作業流程：盾構機停機，確定需要更換刀具的具體位置；機械臂帶動末端手爪抓取需要更換的磨損刀具；將抓取的刀具帶回艙體內；攜帶新的刀具運動到刀盤相應位置并進行安裝；繼續下一刀具的更換任務；完成換刀任務后，機械臂縮回艙體內，關閉艙門，刀盤旋轉，盾構機繼續工作。

通過分析以上工作流程，總結出機械臂換刀主要面臨以下困難：對換刀機械臂的負載能力有較高要求；盾構機內部空間有限，換刀機械臂應當具有較高的靈活性；工作環境惡劣。

1.2 總體設計

通過綜合考慮換刀機械臂的作業要求和環境限制，確定換刀機械臂為 6 自由度關節構型，即 J1 基座回轉、J2 大臂俯仰、J3 小臂俯仰、J4 腕關節俯仰、J5 腕關節擺動和 J6 腕關節回轉，此外，手爪的開合自由度能實現對刀具抓取。針對盾構機對換刀機械臂的結構緊湊、末端負載較大的需求，機械臂各關節均采用液壓驅動，即通過直線液壓缸、液壓馬達與擺動液壓缸來實現關節的俯仰和擺動。換刀機械臂整體結構如圖 1 所示。

圖1 盾構機換刀機械臂的整體結構Fig.1 Overall structure of tool-changing manipulator for shield machine

2 運動學分析

2.1 換刀機械臂正運動學分析

換刀機械臂為六自由度開鏈機構，采用標準D-H 參數法將連桿固定形成坐標系，則機械臂的連桿坐標系如圖 2 所示，其具體 D-H 參數如表 1 所列。

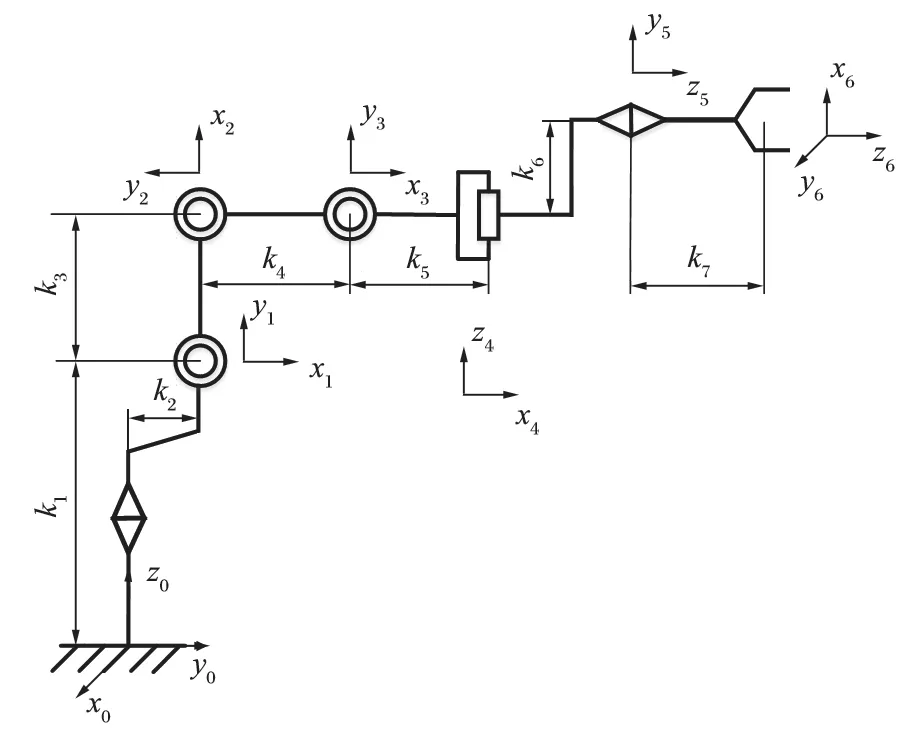
圖2 換刀機械臂連桿坐標系Fig.2 Linkage coordinate system of tool-changing manipulator

表1 機械臂的 D-H 參數Tab.1 D-H parameters of manipulator

表1 中，k1=200，k2=140，k3=880，k4=560，k5=175，k6=40，k7=552。

連桿坐標系間的變換為

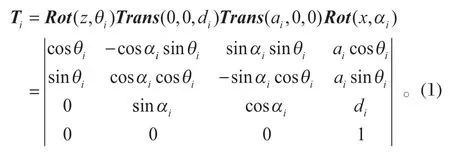
將表 1 中的參數代入式 (1)，獲得相鄰連桿坐標系之間的齊次變換矩陣T1、T2、T3、T4、T5、T6，則換刀機械臂末端手爪在基坐標系下的位姿可表示為

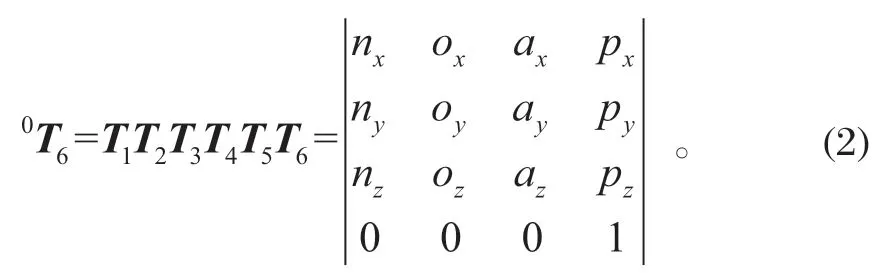
式中：[nx ny nz]T、[ox oy oz]T、[ax ay az]T為機械臂末端相對于基座坐標系的姿態向量；[px py pz]T為機械臂末端在基坐標系的位置向量。

2.2 換刀機械臂逆運動學分析

根據機械臂在基坐標下的末端位姿，進行關節角的求解就是機械臂的逆問題。由于所研究的機械臂滿足 Pieper 法則，即第 2、3、4 關節的軸線相互平行，因此通過解析法進行機械臂的逆運動學求解。

(1)首先，已知機械臂末端在基坐標下的位姿如式 (2)所示，將式 (2)左乘T1的逆矩陣、右乘T6的逆矩陣，得

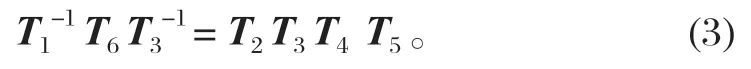
根據式 (3)左、右兩邊矩陣對應的元素相等，由第 3 行第 4 列元素相等，得：

①當k7ay-py=0 時，若k7ax-py＞0，θ1=0；若k7ax-py＜0，θ1=180°。

② 當k7ax-px=0 時，θ1=90°。

③其他情況下，

(2)由式 (3)兩邊矩陣第 3 行第 3 列元素相等得

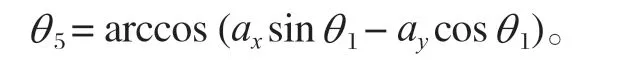
(3)由式 (3)兩邊第 3 行第 2 列元素相等得：

①當oycosθ1-oxsinθ1=0 時，若nycosθ1-nxsinθ1＞0，θ6=0；若nycosθ1-nxsinθ1＜0，θ6=180°。

② 當nycosθ1-nxsinθ1=0 時，θ6=90°。

③其他情況下，

(4)由于機械臂的第 2、3、4 關節軸線平行，因此構成圖 3 所示的平面 2R 機械臂，此時第 2 關節的坐標原點o1為該 2R 機械臂的基座，第 4 關節的坐標原點o3為機械臂的末端。機械臂末端o3在基坐標系o1下的位姿為

圖3 第 2、3、4 關節構成的平面 2R 機械臂Fig.3 2R plane manipulator consisting of joint 2,3,4

由于式 (4)右端矩陣第 1 行第 4 個元素r(1,4)、第2 行第 4 個元素r(2,4)分別表示o3在o1下的笛卡爾坐標，因此

在△o1o2o3中，由余弦定理得

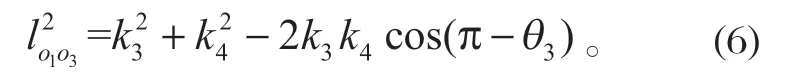
根據式 (5)、(6)得

(5)由于

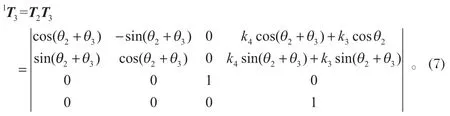
式 (7)與式 (4)第 3 行第 1 列元素相等，且其本體結構的限制θ4∈[20°，65°]，因此θ4有唯一解，

θ4=-arctan (cosθ5(sinθ6(oycosθ1-oxcosθ1)-cosθ6(nycosθ1-nxsinθ1))-sinθ5(aycosθ1-axsinθ1))/(sinθ6(nycosθ1-nxsinθ1)+cosθ6(oycosθ1-oxsinθ1))。

(6)由式 (7)與式 (4)第 2 行第 2 列元素相等，得θ2=arccos (sinθ4(azsinθ5+cosθ5(nzcosθ6-ozsinθ6))+cosθ4(ozcosθ6+nzsinθ1))-θ3。

3 MATLAB 仿真驗證

3.1 運動學仿真

為進行運動學分析驗證，隨意給定機械臂 1 組關節向量θ=[π/2，π/6，-π/3，π/3，π/2，0]T，將其代入機械臂式 (2)，則末端相的位姿矩陣

為進行驗證，通過 Robotics Toolbox 進行機械臂的建模，并給定機械臂的關節變量θ=[π/2，π/6，-π/3，π/3，π/2，0]T，機械臂的位姿如圖 4 所示，仿真結果的位姿與式 (8)理論計算結果一致，表明運動學計算的正確性。

圖4 給定關節變量換刀機械臂的位姿仿真Fig.4 Posture simulation of tool-changing manipulator at given joint parameters

3.2 可達工作空間分析

工作空間表示機械臂末端執行器所能到達的空間幾何，是機械臂的重要指標之一[3-4]。

借助 MATLAB 軟件，基于蒙特卡羅法，采用隨機取樣的方法隨機生成機械臂的關節變量值，然后將其代入式 (2)，生成隨機的機械臂末端參考點。大量隨機的末端參考點構成如圖 5 所示的工作空間云圖。由于機械臂的主要工作面為盾構機的軸截面，即基坐標系下的y0o0z0平面，因此，令θ1=90°，其他關節為隨機值，可獲得圖 6 所示的機械臂活動范圍。

圖5 機械臂工作空間云圖Fig.5 Contours of manipulator workspace

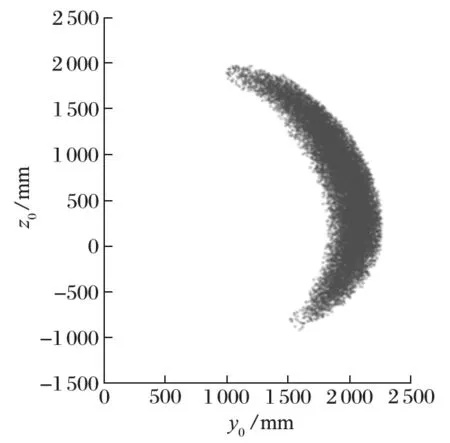
圖6 工作空間在 o0y0z0平面的截面Fig.6 Section of workspace on plane o0y0z0

從圖 5、6 中可以獲得換刀機械臂的主要作業范圍：最大作業半徑為 2 270 mm；最大作業高度為 2 000 mm；最大作業深度為 920 mm。即機械臂的作業空間較大，可滿足盾構機對作業空間的需求。

3.3 軌跡規劃研究

由于關節空間下的路徑規劃[5]能直接反映出機械臂各關節的運動情況，因此筆者采用五次多項式插值在關節空間下進行軌跡規劃。設規劃時間tf=30 s，機械臂的初始位姿對應的關節量θ(0)=[π/4，π/3，-π/4，π/3，5π/4，0]T，目標點位姿對應的關節量θ(30)=[π/2，π/6，-π/3，π/4，π/2，π/4]T，通過五次多項式插值，獲得各關節角位移曲線、角速度曲線、角加速度曲線分別如圖 7～9 所示。

圖7 各關節角位移曲線Fig.7 Angular displacement curves of various joints

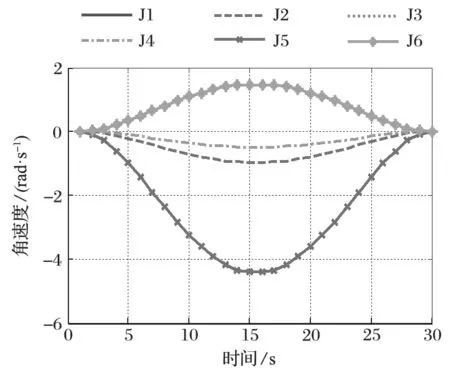
圖8 各關節角速度曲線Fig.8 Velocity curves of various joints

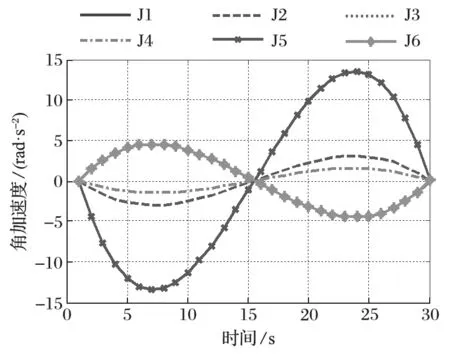
圖9 各關節角加速度曲線Fig.9 Angular acceleration curves of various joints

通過軌跡規劃仿真發現，采用五次多項式插值后，各關節的角位移、角速度、角加速度曲線都較為光滑，能夠用于實現機械臂的動作。由圖 7 可知，各關節角速度在 15 s 時最大，并且在 30 s 時，各關節速度為零，停止動作；由圖 8 可知，各關節角加速度服從正 S 曲線，先為正，后為負，并且在 30 s 時速度都為零 (J1 與 J6 關節角速度曲線重合、J3 與 J4 關節角速度曲線重合)；由圖 9 可知，第 5 關節在動作過程中角加速度較大 (J1 與 J6 關節角加速度曲線重合、J3 與 J4 關節角加速度曲線重合)，因此其驅動力矩也應最大，在進行液壓系統設計與控制時，應加以注意。

4 結論

通過對盾構機換刀任務進行分析，設計了一種針對盾構機換刀的液壓換刀機械臂。針對機械臂的構型特點，建立各連桿坐標系，對其進行運動學建模，獲得末端手爪相對于基座的位置坐標和關節空間與笛卡爾空間的映射關系。借助 MATLAB 軟件，基于蒙特卡羅法，得到機械臂的工作空間云圖，獲得其工作范圍。采用 MATLAB 軟件進行機械臂關節空間下的五次多項式軌跡規劃，仿真結果表明，機械臂動作平穩，為機械臂的設計開發和后續的研究提供參考。