彈塑性損傷蠕變模型的有限元數值實施
崔 賢,張 濤,黃文雄
(河海大學 力學與材料學院,江蘇 南京 210098)
隨著地下洞室開挖、油氣儲存、核廢料處理等項目的增多,軟巖流變特性對工程的安全性和穩定性影響已經成為國內外地下工程領域的熱點問題,建立能夠描述軟巖流變特性的本構模型變得至關重要,對于地下工程的變形和破壞的合理預測具有重要的工程意義[1-2]。
國內外學者對軟巖的非線性蠕變進行了大量研究,Cristescu等[3]主要研究了巖石的蠕變試驗、損傷機理、本構關系以及斷裂問題;Adachi等[4]提出了一個可以同時描述軟巖硬化和軟化的本構模型。Jia等[5]根據泥巖的三軸試驗結果,建立了在飽和狀態和非飽和狀態下都能適用的彈塑性損傷本構模型。在與時間相關性方面,Borja等[6]建立了三維應力狀態下濕黏性土與時間相關的本構模型。Shao等[7]提出了一個短期可以描述彈塑性行為,長期可以描述巖石蠕變的本構模型。Hunsche等[8]建立了一個彈黏塑性非線性的鹽巖力學模型,該模型可以模擬鹽巖的損傷、斷裂和膨脹。
肖欣宏等[9]利用Burgers模型和非線性黏彈塑性模型對水環境下紅層軟巖蠕變進行了研究。賈善坡等[10]在修正Mohr-Coulomb準則中引入了損傷變量建立了反映泥巖軟硬化的本構模型。楊春和等[11]通過對鹽巖蠕變試驗研究,提出了一個鹽巖非線性蠕變本構方程。姜永東等[12]根據不同應力水平產生的蠕變差異,建立了砂巖的蠕變本構模型。
ABAQUS材料庫中的巖土類模型都是比較經典的本構模型,不能很好地描述軟巖流變特性,為了彌補這一不足,利用ABAQUS提供的用戶材料二次開發接口,對Shao等[7]模型的進行了有限元數值實施。該模型數學公式簡單,參數不多且容易通過基本試驗確定,能夠描述軟巖的三軸試驗和體應變特點,并且能進一步考慮軟巖的流變特性。采用Fortran語言編寫了UMAT子程序,將模擬的結果和試驗數據進行對比,進一步驗證模型和程序的可靠性。
1 本構模型
本文采用的本構模型[6]包含兩部分,即彈塑性模型和考慮塑性損傷的蠕變模型,基礎模型描述軟巖的短期力學響應,擴展模型能反映軟巖在較長時段內的蠕變變形。
1.1 彈塑性模型
基礎模型假定材料在應力空間中的屈服面與破壞面相似。采用的強度條件在p-q坐標系(應力平面)的軌跡為拋物線,如圖1所示。該模型屈服函數為:
q2+Apr(p-C0)=0
(1)
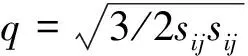
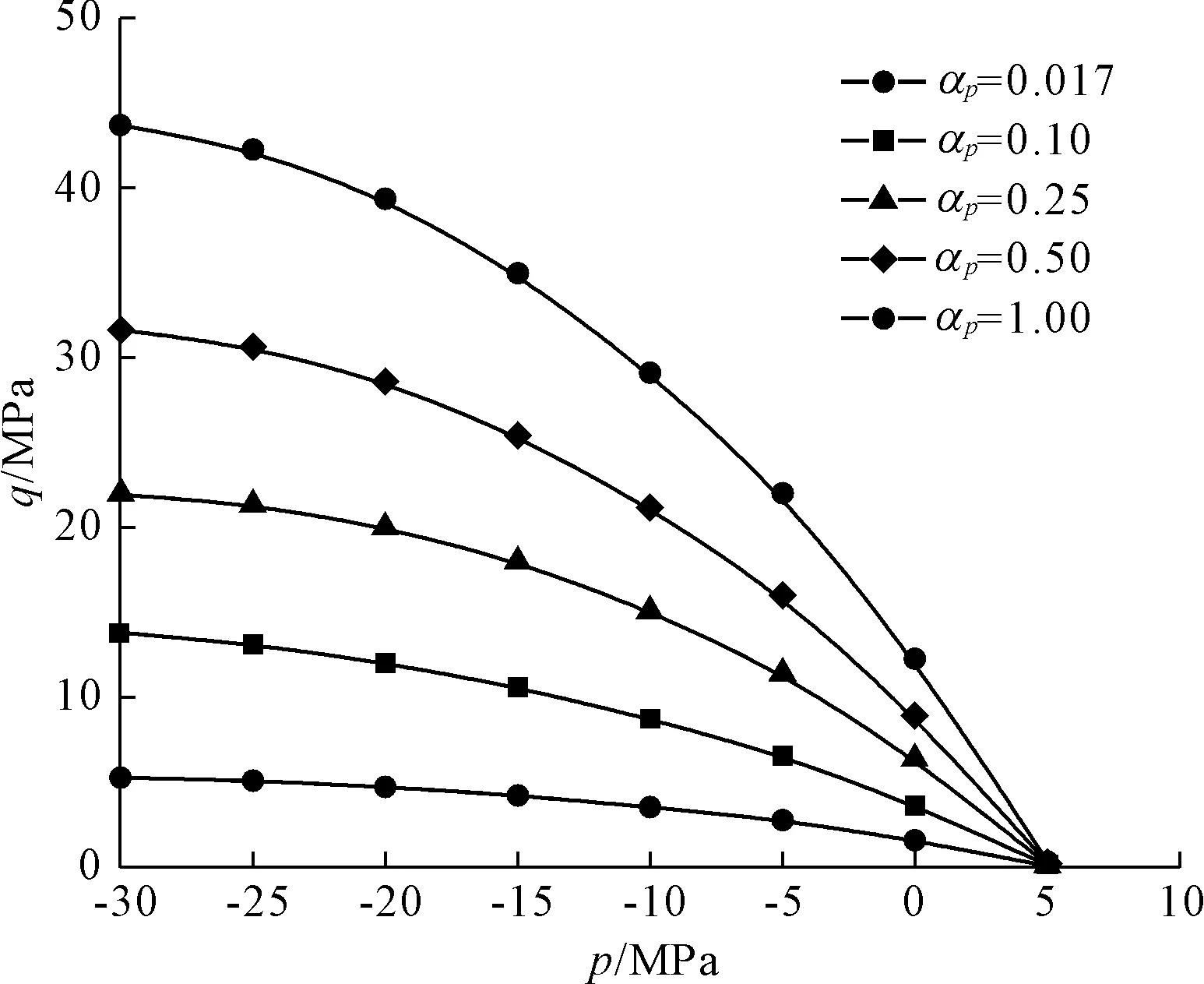
圖1 破壞面和屈服面形態
材料在偏應力作用下的屈服條件采用與強度條件相似的數學表達:
f(p,q,γp)=q2+αp(γp)Apr(p-C0)=0
(2)
式中:αp是硬化變量,依賴于塑性應變。
(3)
(4)
該模型采用了非關聯流動法則,塑性函數采用與原始劍橋模型相似的形式:
(5)
式中:η是另外一個材料參數,該參數確定塑性勢面水平切線點連線的斜率;p1是塑性勢面與p軸左邊交點的坐標(見圖2),與計算塑性應變增量的應力點(當前應力狀態)有關。
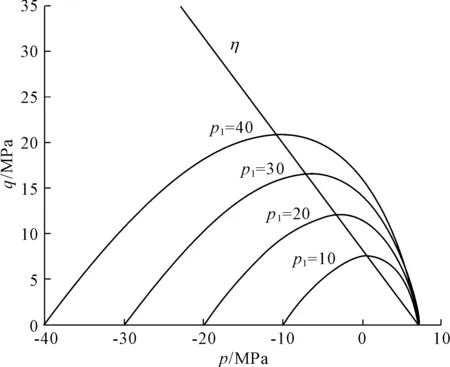
圖2 塑性勢面形態
1.2 擴展的彈-黏塑性模型
上述模型經過擴展后,可考慮流變效應,用以預測軟巖的長期變形。具體的做法是仿照Pitruszczak等[13],引進一個時變損傷變量 ,用于描述剛度和強度隨塑性變形發展而下降的規律:
E=(1-αζ)E0,A=(1-α1ζ)A0
(6)
式中:E0是初始楊氏模量,α描述剛度損傷,α1描述強度損傷。
建議的損傷變量演化規律為:
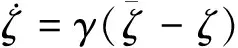
(7)
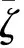
(8)
2 有限元數值實施
利用ABAQUS材料二次開發接口,可將上述模型編成UMAT子程序用于有限元數值分析。數值實施需要在一個典型的時間增量步[tn,tn+1] 上,在已知應力狀態σn和應變增量Δε求出的條件下,根據本構關系求出應力增量更新應力,并且給出下一步計算的材料雅可比矩陣。具體如下。
2.1 隱式應力積分回映算法
彈塑性模型的應力積分一般在彈性預測基礎上,判斷加卸載。對于塑性加載步,本文采用隱式應力積分回映算法,將超出屈服面的應力調整返回到屈服面[8-9](見圖3)。
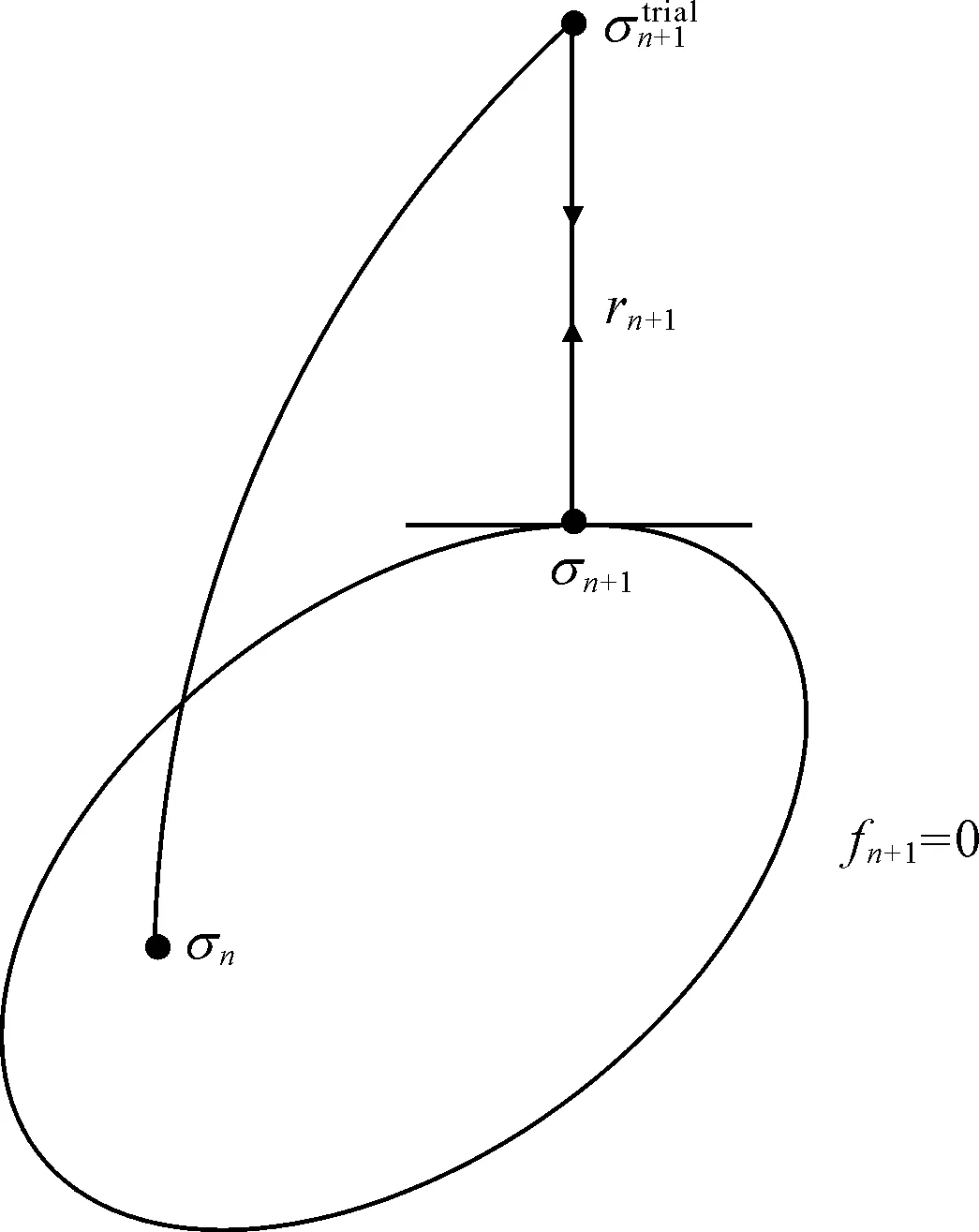
圖3 隱式應力積分回映算法示意圖
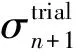
(9)
式中: Δσe為彈性應力增量,De為彈性矩陣。

(10)
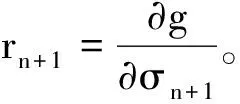
按隱式積分格式,計算塑性應變和內變量增量:
(11)
式中:
(12)
采用牛頓法對非線性方程組(11)求解,在算法的塑性修正階段中,總應變是一個定值,線性化只有一個變量,即塑性應變因子增量Δλ。
牛頓法中應用如下標記:方程g(Δλ)=0線性化,令Δλ(0)=0:
(13)
式中:δλ(k)是在第k次迭代時Δλ的增量。
為了適應牛頓迭代法,以公式(13)的形式寫出公式(11)中的塑性更新變量和屈服條件,省略公式角標n+1:
(14)
線性化后:
(15)
式中:
(16)
(17)
式中:
(18)
由公式(17)可知應力和硬化變量增量:
(19)
將結果(19)代入(15)3求解δλ(k)
(20)
式中:?f=[fσfαp]
參數更新后:
(21)
多次使用牛頓迭代法,直到結果收斂到更新屈服表面誤差范圍內。
2.2 一致性切線剛度矩陣推導
應力應變關系為:
(22)
增量形式
(23)
根據流動法則,塑性應變增量
(24)
其中:
(25)
把式(24)代入式(23)得到
(26)
式中:dλ由加載的一致性條件確定
(27)
其中:dαp=(dαp/dλ)dλ依賴塑性應變,dA=(dA/dζ)dζ依賴損傷變量。
對df展開后得到:
(28)
其中:
(29)
把dλ代入式(26)
(30)
式中:
(31)
(32)
2.3 算法更新流程
第1步,設置初始值。損傷變量ζ是時間的顯函數,假定損傷變量ζ=0,利用式(8),在當前值ζ(t)已知的情況下,對給定的時間增量,利用積分中值定理
θ∈(0,1)
(33)
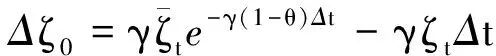
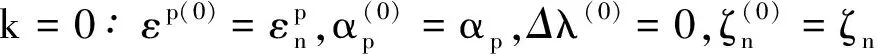
σ(0)=(1-αΔζ0)σn+DnΔε-Dnεp(0)
(34)
其中:Dn=(1-αζn)De。
第2步,第k次增量步后,檢查屈服函數收斂性。
(35)
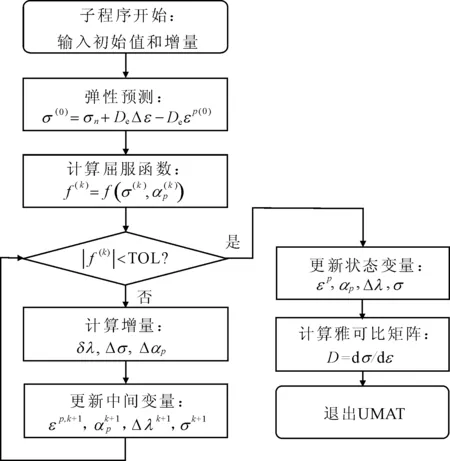
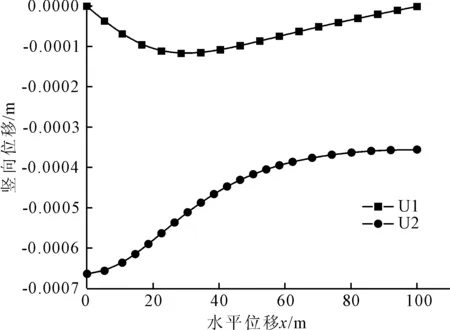
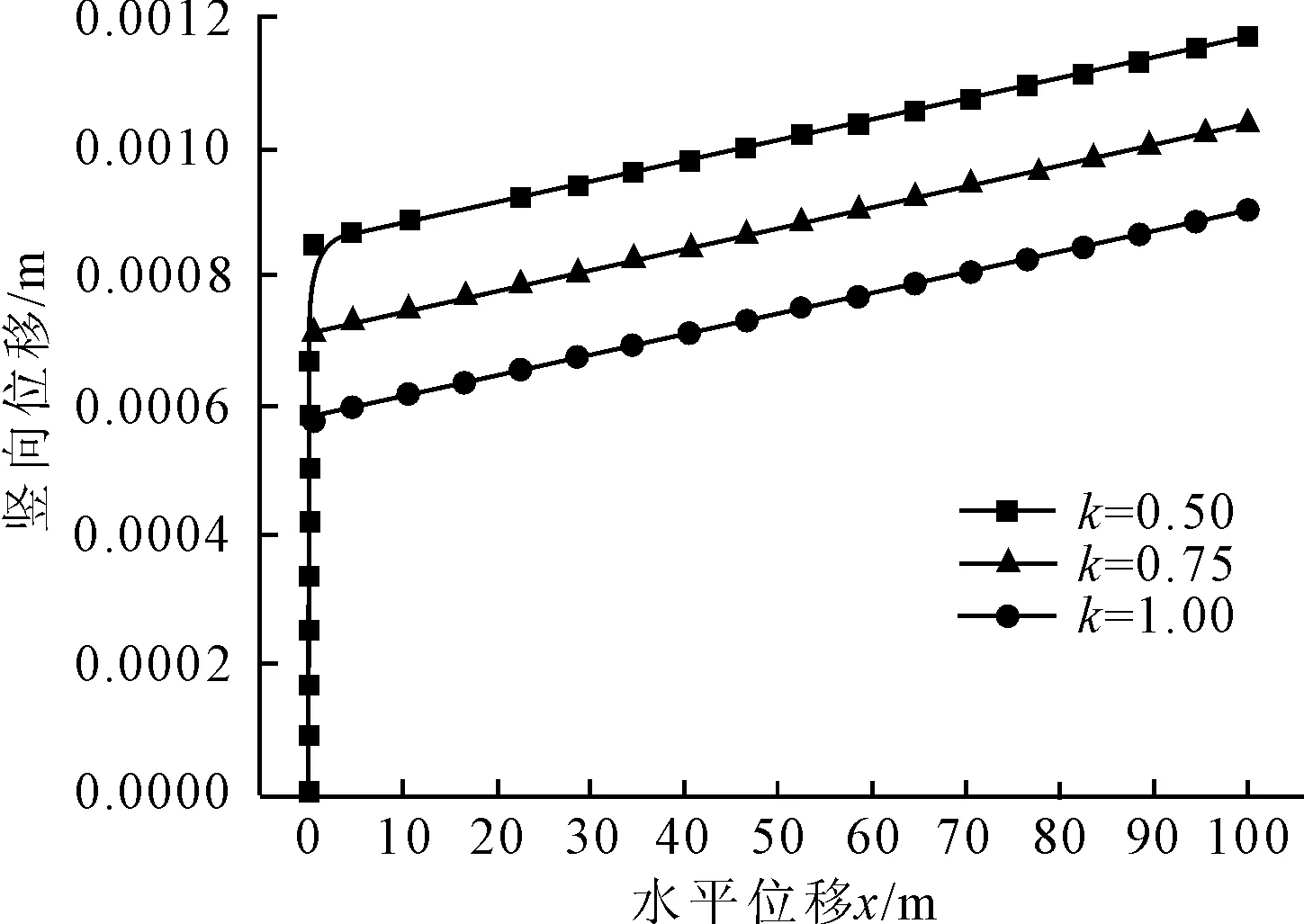
若f(k) 第3步,計算塑性參數的增量。 (36) 第4步,得到應力和硬化變量的增量。 (37) 第5步,更新變量。 (38) 令k=k+1,轉到第3步 。 有限元商業軟件ABAQUS提供了UMAT子程序接口[15],供用戶創建自定義材料模型。在增量步開始時,主程序在積分點上調用UMAT,根據傳入的應變增量和狀態變量,計算出雅可比矩陣(見圖4)。 圖4 UMAT子程序分析流程圖 利用該本構模型在ABAQUS軟件中開發了UMAT子程序,對不同圍壓下三軸壓縮試驗和單軸蠕變試驗進行有限元數值模擬,將模擬結果與試驗結果相比較,用以測試UMAT程序的可行性和準確性。 常規三軸壓縮試驗設置了2個圍壓等級,分別為2 MPa和10 MPa。試驗的試樣為標準試樣(直徑50 mm,高100 mm)(模型見圖5),試驗加載采用軸向應變控制方式,對試樣施加豎向位移2 mm。材料參數見表1。 表1 算例1的模型參數 圖6和圖7分別為圍壓2 MPa和10 MPa時的試樣應力-應變曲線和體積應變曲線。從圖6和圖7可以看出,該模型的彈塑性模擬和試驗結果有較好的一致性,但是10 MPa圍壓下的模擬結果比試驗結果稍小,原因是在更高的圍壓條件作用下,材料的之間的孔隙受到壓縮變小,使彈性模量變大,導致模擬的結果偏小。材料的體積應變曲線前期的結果與試驗比較符合,后期材料進入破壞階段,出現了小偏離。 圖5 三軸壓縮試驗分析模型 圖6 圍壓為2 MPa時應力-應變和體積應變曲線 圖7 圍壓為10 MPa時應力-應變和體積應變曲線 試樣模型不變,進行了單軸蠕變模擬,首先在試樣垂直方向施加均布荷載力,其值從0 MPa逐漸增加到48.5 MPa,然后保持不變。蠕變模型新增加了三個新參數,取值如表2所示。 圖8為單軸壓縮蠕變試驗模擬曲線,從圖8中可以看出,模擬結果和蠕變的試驗結果都較為相似,該模型可以表征該類泥巖的蠕變變形性能。 表2 算例2的模型參數 圖8 單軸壓縮蠕變試驗模擬曲線 為了進一步驗證模型的蠕變特性,建立一個地下無支護洞室對稱二維模型,尺寸如圖9所示,巖體參數選取依據為上述試驗結果,巖體容重2.0×104N/m3,側壓力系數k=0.5,總時間T為100 d,固定左右邊界的水平位移和底部邊界的豎向位移,對其進行計算分析。 圖9 地下洞室模型示意圖(單位:m) 圖10為開挖后的Mise云圖;圖11為巖體表面的水平位移和豎向位移圖;圖12為不同側壓力系數下洞頂位移隨時間變化圖。由圖10可知開挖后的應力變化,右側頂部和底部的應力比較大,應該作為重點加固區域。從圖11可見,靠近中心線的巖體表面處的豎向位移最大,當離中心線距離增大時豎向位移逐漸減小,而水平位移的方向指向中心線,反映了變形方向指向開挖面。為了研究不同側壓力水平對開挖位移的影響,由圖12可知,豎向位移隨k的增大而減小,不同的側向應力只對開挖完成時的變形有影響,而后期蠕變的增長趨勢保持一致。 圖10 開挖后Mises應力云圖 圖11 巖體表面的水平位移和豎向位移圖 圖12 不同側壓力系數下洞頂豎向位移隨時間變化 (1) 利用ABAQUS提供的UMAT子程序接口,實現了泥巖彈塑性損傷模型的二次開發。該模型簡單易懂,物理意義明確,能夠較好地反映泥巖的彈塑性變形和蠕變變形特性。 (2) 算例結果顯示,所采用的隱式積分回映算法具有很高的精確度和收斂性,能夠利用本模型反映軟巖的應力應變特性。 (3) 工程實例模擬結果符合實際,可以為大型復雜應力狀態下的地下工程數值分析提供合理的建議,擴大了ABAQUS在巖土工程中的應用范圍,同時也為開發其他巖土類的本構模型提供了參考。3 UMAT二次開發
4 有限元程序驗證
4.1 不同圍壓常規三軸壓縮試驗模擬
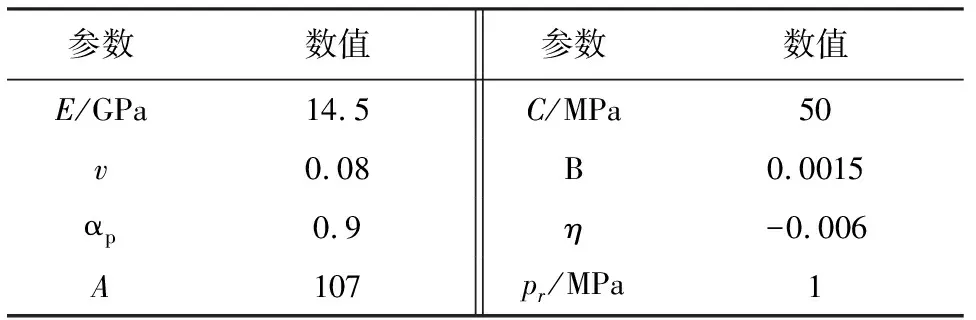



4.2 蠕變試驗模擬

5 開挖算例

6 結 論

