錨桿加固恩施大峽谷絕壁危巖的穩定性數值分析

譚朝瑞,王明華,付 強,袁 飛,劉易然

(湖北省地質局第二地質大隊，湖北 恩施 445000)

錨桿錨固技術已成為一種不可替代的巖土工程安全加固措施，在邊坡巖體經過開挖卸載后，表層失衡的自重應力場通過錨固作用得到適當恢復，主要作用為對表層卸荷巖體的壓實壓密，增韌止裂，提高巖體整體性與變形均勻性，降低了局部破壞的機率，形成了新應力狀態的良性調整[1-3]。因此許多專家學者通過理論計算或者監測數據分析的方法也對錨桿部分加固參數與穩定性的關系做出來了許多創新性的研究[4-9]。有限元法作為一種運用廣泛的數值分析方法，具有功能強大，分析結果明確等優點，一些學者結合錨桿的部分加固參數，也開展了數值模擬方面的研究[10-17]。本文采用ABAQUS有限元軟件，對錨桿加固參數的作用效果進行分析，分別選取錨桿的長度、入射角、數量、間距多情況進行模擬，并進行綜合對比分析，得到大峽谷絕壁棧道危巖加固最為經濟安全的選擇。

1 危巖概況

絕壁陡崖危巖位于湖北省恩施大峽谷絕壁棧道景區，屬構造剝蝕侵蝕中低山區，出露地層巖性主要為三疊系下統大冶組三段(T1d3)薄層狀灰巖，呈近水平產出，風化程度不均，整體呈微—中風化，局部陡崖頂有少量第四系全風化層，單層厚度一般8 cm～15 cm，總層厚約1 m～2 m。

如圖1所示，危巖分布高程1 767.4 m～1 788.2 m，總體呈巨塊狀，整體高約21 m，平均寬約8 m，平均厚度4 m，體積約672 m3。危巖受兩組垂直的裂隙切割，正面、右側臨空，底部完全懸空，只有左側和后部與母巖相連。

圖1 危巖基本特征

2 研究方法

本次模擬采用ABAQUS有限元分析軟件開展數值模擬研究。ABAQUS有限元模擬中危巖邊坡穩定極限平衡方法采用Mohr-Coulomb屈服準則，安全系數定義為沿滑動面的抗剪強度與滑動面上實際的剪力的比值，用公式表示如下：

(1)

式中:ω、s和τ分別為安全系數、滑面上的抗剪強度和滑面上的實際剪切力；c、φ分別為巖體的黏聚力和內摩擦角。將式(1)中強度參數除以ω得到：

(2)

(3)

有限元強度折減法通常采用下式定義安全系數：

(4)

式中:I1和J2分別為應力張量的第一不變量、應力偏量的第二不變量；α和k是與巖土材料黏聚力c和內摩擦角φ有關的常數，采用與Mohr-Coulomb準則等面積圓的廣義米賽斯屈服準則，計算的塑性區反映圍巖實際塑性區的大小，廣義米賽斯屈服準則的系數α和k為：

(5)

(6)

可見，在D-P準則中α和k折減的同時，c和tanφ也有同步折減關系，式(5)和式(6)是兩者折減系數間換算關系。式(4)中，ω是強度折減法中安全系數的定義。強度折減有限元方法的基本原理是將巖體強度參數黏聚力c和內摩擦角φ同時除以一個折減系數ω,得到一組新的c′和φ′值，作為新材料參數輸入，進行試算；當計算不收斂時，對應的ω值為邊坡的最大穩定安全系數。

本文采用了未降雨和降雨后兩種工況模擬危巖的穩定性，模擬參數如表1所示。

選用危巖的防護治理為研究對象，考慮其不同錨桿參數選擇在穩定性的區別，參數選擇如表2所示。

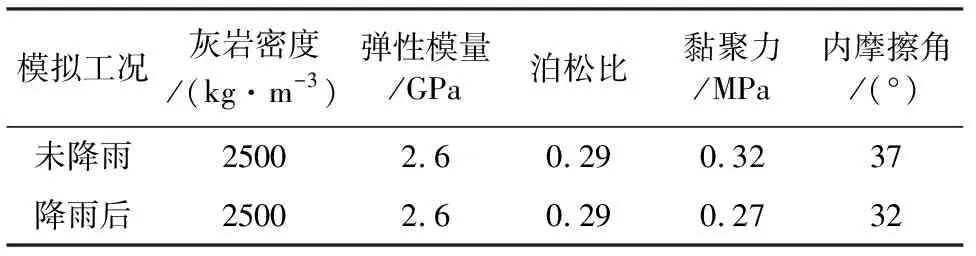
表1 灰巖模擬參數

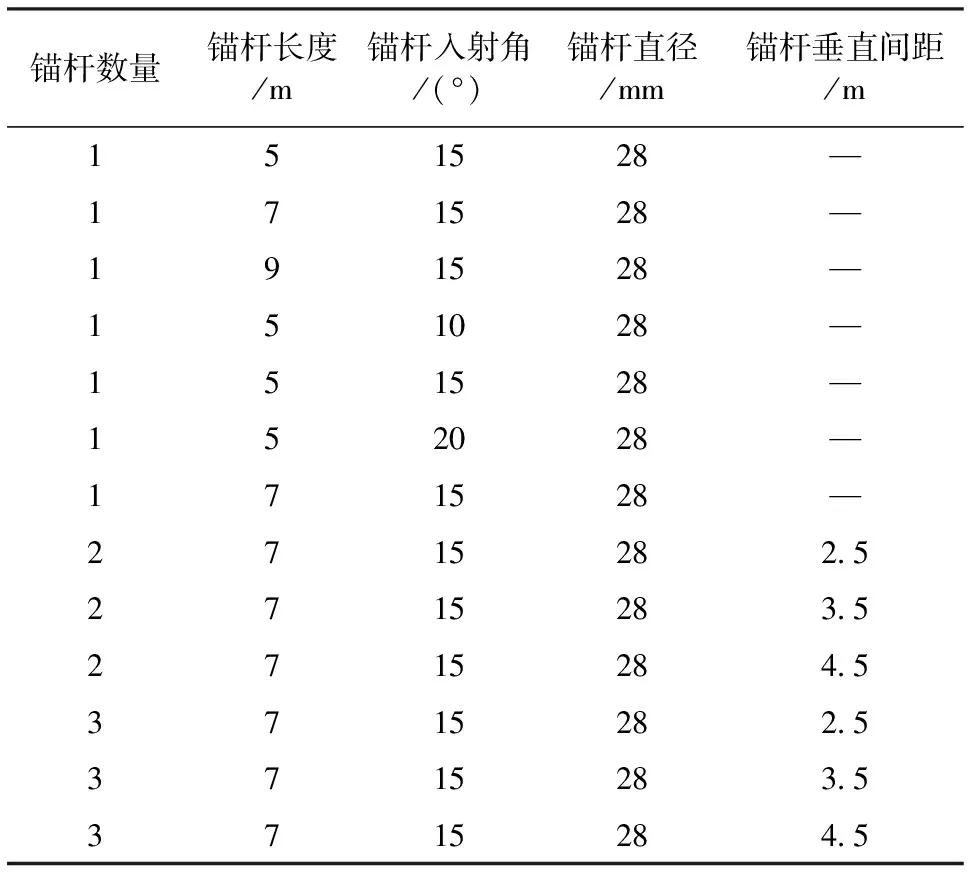
表2 錨桿加固參數選擇

其中模型參數不變，在危巖位置加設錨桿，根據錨桿物理力學參數，彈性模量取210 GPa，泊松比取0.3，密度取7 850 kg/m3。模擬云圖結果應力單位為Pa，位移單位為m。根據危巖和實際工程情況，錨桿直徑統一為28 mm，且長度不宜過長，因此選取5 m、7 m、9 m三種錨桿長度，根據不同錨桿長度布置圖如圖2所示。

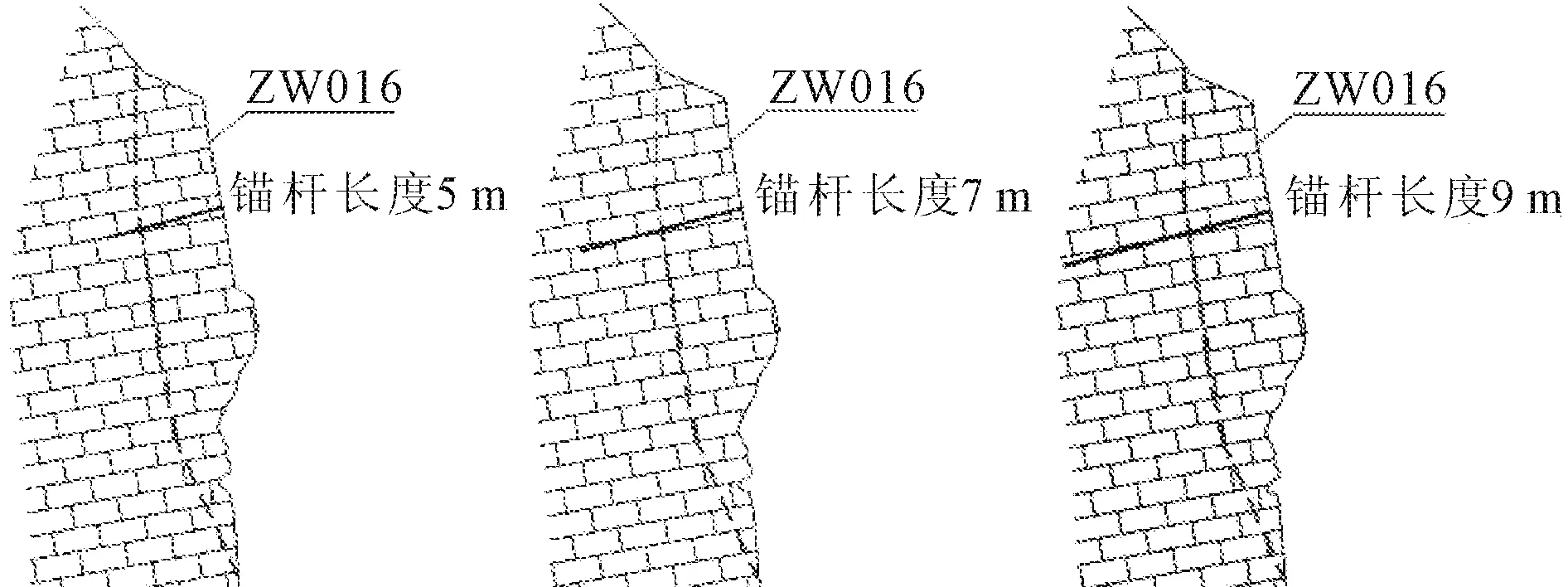
圖2 不同錨桿長度布置圖

錨桿入射角一般取值在10°～25°之間，當錨桿入射角度<5°時，錨桿注漿施工難度大，漿液不容易到達錨桿底部；當錨桿入射角度>25°時，錨桿提供的水平力比較小了，造成錨桿浪費，因而選取10°、15°、20°作為入射角的參數選擇，如圖3所示。

與此同時，在危巖錨桿治理中，通常會考慮使用多根錨桿共同作用，考慮了縱向2根、3根錨桿設置，錨桿間距分別為2.5 m、3.5 m、4.5 m，如圖4、圖5所示。

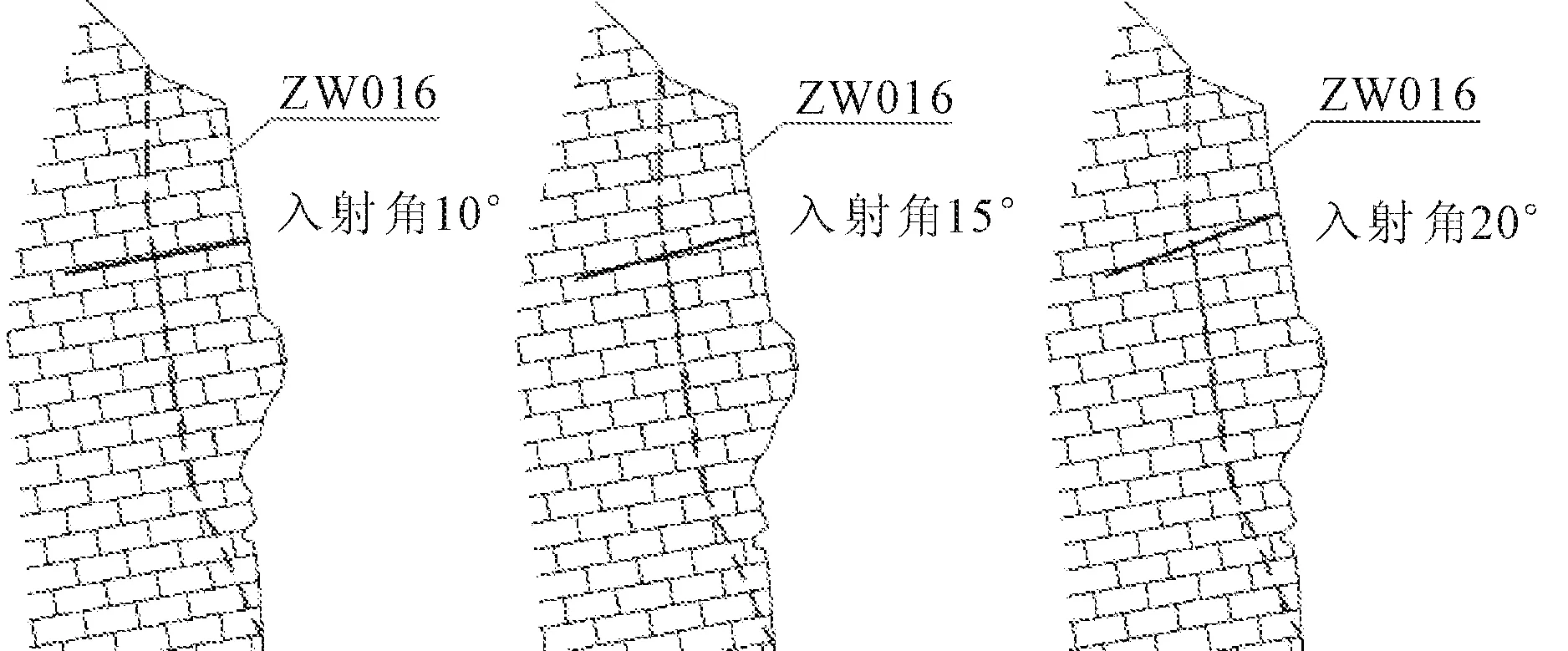
圖3 不同錨桿入射角布置圖

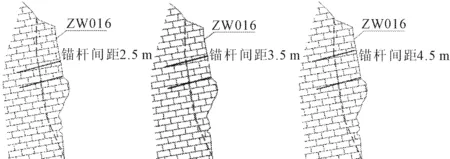
圖4 2根不同錨桿間距布置圖

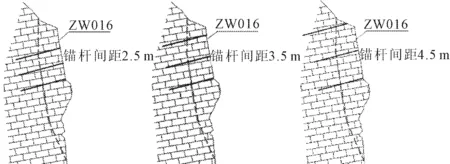
圖5 3根不同錨桿間距布置圖

3 有限元數值模擬研究

3.1 單根錨桿不同加固參數危巖穩定性的有限元模擬

3.1.1 塑性應變結果分析

如圖6所示，設置錨桿后塑性應變的分布區域不變，但應變值都有所減小，且平均最大塑性應變值相比未設錨桿降低了47.1%，但增大錨桿長度幾乎不能影響塑性應變值的最大值和分布，對于后續的應力和位移分布也同樣如此。因此，當錨桿長度超過推測滑動面時，持續增大錨桿長度并不能很好的提高危巖的防護效果，達到增強穩定性的效果。

如圖7所示，入射角在10°～15°之間，每增加1°最大塑性應變值就增加7.1×10-4；入射角在15°～20°之間，每增加1°最大塑性應變值就增加16×10-4。因而，錨桿入射角越大，最大塑性應變值也越大，塑性應變值的增大的速度也越快。

3.1.2 應力結果分析

如圖8所示，最大應力集中在錨桿下部潛在滑動面附近，入射角在10°～15°之間，每增加1°最大應力就增加1.02×108Pa；入射角在15°～20°之間，每增加1°最大塑性應變值就增加1.72×106Pa。因而，錨桿入射角越大，錨桿的最大應力也越大，但最大應力的增大的速度越慢。

圖6 單根不同長度錨桿塑性應變值云圖

圖7 單根錨桿不同入射角塑性應變值云圖

圖8 不同入射角單根錨桿應力云圖

3.1.3 位移結果分析

如圖9所示，增設錨桿后能明顯降低危巖的水平位移，其中平均最大水平位移降低0.107 m，相比未設錨桿降低47.7%，但其總體的分布特征不會改變。入射角在10°～15°之間，每增加1°最大水平位移就增大0.001 7 m；入射角在15°～20°之間，每增加1°最大水平位移就增大0.003 5 m。因而，錨桿入射角越大，危巖的最大水平位移也越大，且最大水平位移增大的速度越快。

如圖10所示，增設錨桿后能明顯降低危巖的垂直位移，其中平均最大垂直位移降低0.077 m，相比未設錨桿降低29.5%，但其總體的分布特征不會改變。入射角在10°～15°之間，每增加1°最大垂直位移就增大0.001 2 m；入射角在15°～20°之間，每增加1°最大垂直位移就增大0.002 4 m。因而，錨桿入射角越大，危巖的最大垂直位移也越大，且最大垂直位移增大的速度越快。

圖9 不同入射角單根錨桿水平位移云圖

圖10 不同入射角單根錨桿垂直位移云圖

綜上所述，錨桿入射角越大，對危巖的控制效果和安全性就越差，對于危巖的最大塑性應變值、最大水平位移、最大垂直位移，隨著入射角增大，變化速度越快；而對于危巖的應力而言，則變化速度越慢，但入射角的變化，并不會改變它們的分布特征。因此選取較小的錨桿入射角，能夠提高危巖的安全性，這和施工中的實際經驗是相符合的。

3.2 2根錨桿不同間距參數危巖穩定性的有限元模擬

3.2.1 塑性應變結果分析

如圖11所示，設置2根錨桿時，錨桿間距為2.5 m對塑性應變的控制效果最好，相比未設置錨桿減小了72.8%，間距3.5 m和4.5 m則相比未設置錨桿減小了57.0%和58.0%。

圖11 2根錨桿不同間距的塑性應變值云圖

3.2.2 應力結果分析

如圖12所示，設置2根錨桿時，間距分別2.5 m、3.5 m、4.5 m時錨桿的最大應力分別為1.591×109Pa、2.051×109Pa、1.815×109Pa，即錨桿間距為2.5 m時對應力的控制效果最好，且相對位置靠下的錨桿承受的應力更大。

圖12 2根錨桿不同間距的應力云圖

3.2.3 位移結果分析

如圖13所示，是否設置錨桿對水平位移的分布特征影響甚微，錨桿間距分別為2.5 m、3.5 m、4.5 m時，相比未設錨桿分別減小了70.5%、58.9%、59.7%，即錨桿間距為2.5 m時對水平位移的控制效果最好。

如圖14所示，是否設置錨桿對垂直位移的分布特征影響不大，錨桿間距分別為2.5 m、3.5 m、4.5 m時，相比未設錨桿分別減小了42.3%、36.4%、36.6%，即錨桿間距為2.5 m時對垂直位移的控制效果最好。

綜上所述，設置2根錨桿時，間距為2.5 m時危巖的安全性和防護效果最好，相比未設置錨桿，能夠降低72.8%的最大塑性應變值、70.5%的水平位移、42.3%的垂直位移；相比間距3.5 m和間距4.5 m，錨桿的最大應力降低了22.4%和12.3%。但錨桿間距的變化，也不會改變塑性應變、應力、位移的分布特征。由于位置靠下的錨桿在所受應力更大，因為建議在實際工程運用中下部錨桿采用施加預應力、增加錨桿直徑、采用高性能錨桿等措施，進一步提高危巖的安全性，達到較好的經濟合理性。

圖13 2根錨桿不同間距的水平位移圖

圖14 2根錨桿不同間距的垂直位移圖

3.3 3根錨桿不同間距參數危巖穩定性的有限元模擬

3.3.1 塑性應變結果分析

如圖15所示，設置3根錨桿后的平均最大塑性應變值相比未設錨桿減小了77.5%，當錨桿間距為4.5 m時，最大塑性應變值分別相比間距2.5 m和間距3.5 m減小了7.0%和0.4%。這說明當錨桿間距越大時，其塑性應變的值越小。因此在施工設計時，考慮加大錨桿間距，有利于減小危巖后部與母巖間的塑性應變值，其安全穩定效果更好。

圖15 3根錨桿不同間距的塑性應變值云圖

3.3.2 應力結果分析

如圖16所示，設置3根錨桿后應力將集中在錨桿下部，主要是在粘結危巖后部和母巖附近，邊坡整體的應力都基本趨于一致，平均最大應力為2.498×104Pa。當錨桿間距過小為2.5 m時，錨桿的最大應力為別為間距3.5 m和4.5 m的1.26倍。因此考慮加大錨桿間距，有利于減小錨桿的應力。

3.3.3 位移結果分析

模型的水平位移云圖如圖17所示，相比未設置錨桿危巖最大水平位移為0.224 m，設置3根錨桿后危巖的最大平均水平位移為0.056 m減小了75.0%，錨桿間距為2.5 m的水平位移相比間距 3.5 m和4.5 m增大了5.1%和4.2%。因此可以認為錨桿間距對危巖的水平位移影響較小。

圖16 3根錨桿不同間距的應力云圖

圖17 3根錨桿不同間距的水平位移云圖

模型垂直位移云圖如圖18所示，相比未設置錨桿危巖最大垂直位移為0.261 m，設置3根錨桿后危巖的最大平均垂直位移為0.146 m減小了45.1%，錨桿間距為2.5 m的垂直位移相比間距 3.5 m和4.5 m增大了1.2%和0.6%。因此可以認為錨桿間距對危巖的垂直位移影響甚微。

圖18 3根錨桿不同間距的垂直位移云圖

綜上所述，設置3根錨桿時，間距為3.5 m和4.5 m時危巖的安全性和防護效果非常接近，相比之下最大塑性應變值、最大應力、最大水平位移、最大垂直位移都相差甚微，分別占錨桿間距4.5 m結果的0.38%、-0.21%、-0.85%、-0.56%。以錨桿間距4.5 m為例，相比未設置錨桿，能夠降低78.0%的最大塑性應變值、75.4%的水平位移、45.1%的垂直位移；且錨桿間距的變化，也不會改變塑性應變、應力、位移的分布特征。由于位置靠下的2根錨桿在所受應力更大，因而建議在實際工程運用中位置偏下的錨桿采用施加預應力、增加錨桿直徑、采用高性能錨桿等措施提高其承載能力。

4 結 論

(1) 采用單根錨桿時，就有限元分析的結果的最大塑性應變值、最大應力、最大位移而言，在超過推測滑動面后不受錨桿長度變化影響，而錨桿入射角越小，對其控制效果越好。

(2) 在同一剖面上采用2根錨桿時，錨桿間距為2.5 m時對最大塑性應變值、最大應力、最大位移的控制效果最好；在同一剖面上采用3根錨桿時，錨桿間距為3.5 m和4.5 m對其控制效果基本一致。這說明為了緩解群錨效應，間距和錨桿的根數緊密相關，當采用錨桿數量較多時，可以適當擴大間距，能夠有利于錨桿發揮其錨固力；而當間距過大時，錨固力在剖面上較為分散，也不利于安全性的控制。

(3) 同一剖面上位置偏下的錨桿受應力更大，這是由于位置偏下的錨桿受邊坡危巖整體的重力和應力較大，因此在實際工程中應加大下部錨桿承受應力的能力。