功果橋大壩壩頂水平位移安全監控指標擬定
汪俊波,李 黎,程 帥,俞年年
(1.西安熱工研究院有限公司,陜西 西安 710054;2.華能瀾滄江水電股份有限公司,云南 昆明 650206)
大壩安全監控指標是對在役大壩的效應量所規定的正常狀態與非正常狀態的界限值。對大壩運行期的監測數據進行指標擬定,合理確定監控指標或預警值,對于大壩運行管理以及狀態評估具有重要的指導意義。
在擬定大壩安全監控指標的眾多方法中,置信區間估計法、典型小概率法較為常用[1],在監測資料豐富可靠的情況下,該兩種方法可取得合理的計算結果[2-4]。查閱相關的文獻,采用典型小概率方法擬定監控指標主要是以正態分布方法居多[4-6],對數正態分布和極值Ⅰ型分布的檢驗方法和計算案例較少。本文對典型小概率方法幾種常用分布檢驗步驟、計算方法進行了歸納和梳理。與此同時,以功果橋大壩為工程依托,選取大壩3號、5 號、8號、10號等四個典型壩段的水平位移測點作為監控點,結合歷史觀測數據,通過典型小概率法和統計模型的置信區間法分別計算了相應壩段的位移監控指標,并對兩種方法計算的結果與歷史極值進行比較分析,進而對監控指標進行綜合擬定,為電廠運行管理和狀態評估提供依據。
1 工程概況
功果橋水電站位于云南省云龍縣大栗樹西側,電站以發電為主,水庫正常蓄水位1 307 m,相應庫容3.16億m3。攔河大壩為碾壓混凝土重力壩,最大壩高105.0 m,壩頂總長361.0 m。壩頂布設16個引張線測點用以監測壩頂的水平位移。工程于2007年10月開工,2011年9月底大壩下閘蓄水,2012年3月工程竣工。
2 指標擬定方法
2.1 典型小概率法
選擇不利荷載組合時的監測效應量xmi,得到一組樣本:
x={xm1,xm2,…,xmn}
(1)
由已知隨機變量x的n個觀測值,其統計量樣本均值μ、標準差σ、變異系數δ可用下列公式估計其統計特征值:
(2)
(3)
(4)
然后,用統計檢驗方法,對其進行分布檢驗,確定分布函數F(x)和概率密度函數f(x)。
令xm為效應量的極值,若當x>xm時,大壩將要出現異常或險情,其概率為:
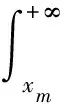
(5)
求出xm的分布后,估算xm的問題轉換為確定大壩出現異常概率α,其值根據大壩的級別和重要性而定[7-11],通常取α=5%,由xm的分布函數直接求出xm=F-1(x,σx,α)。
在工程結構可靠度分析中,對于子樣較少的分布檢驗,通常采用K-S檢驗法,K-S法的步驟為[12-14]:
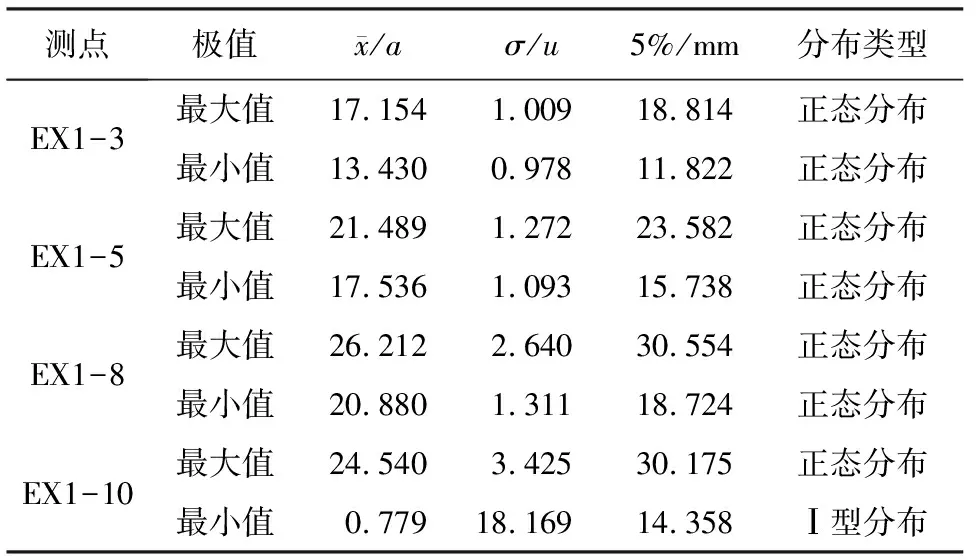
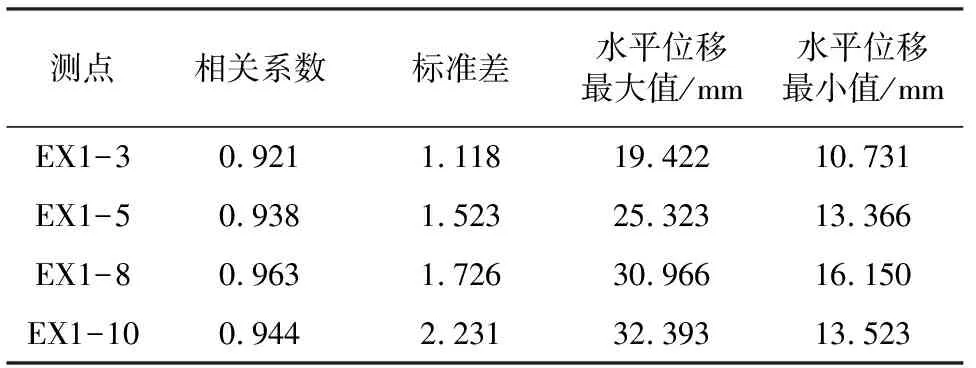
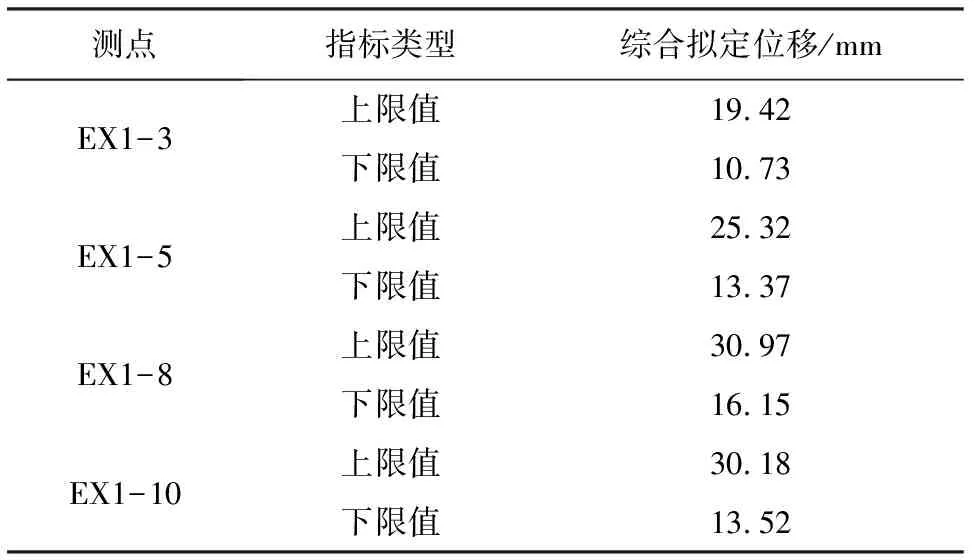
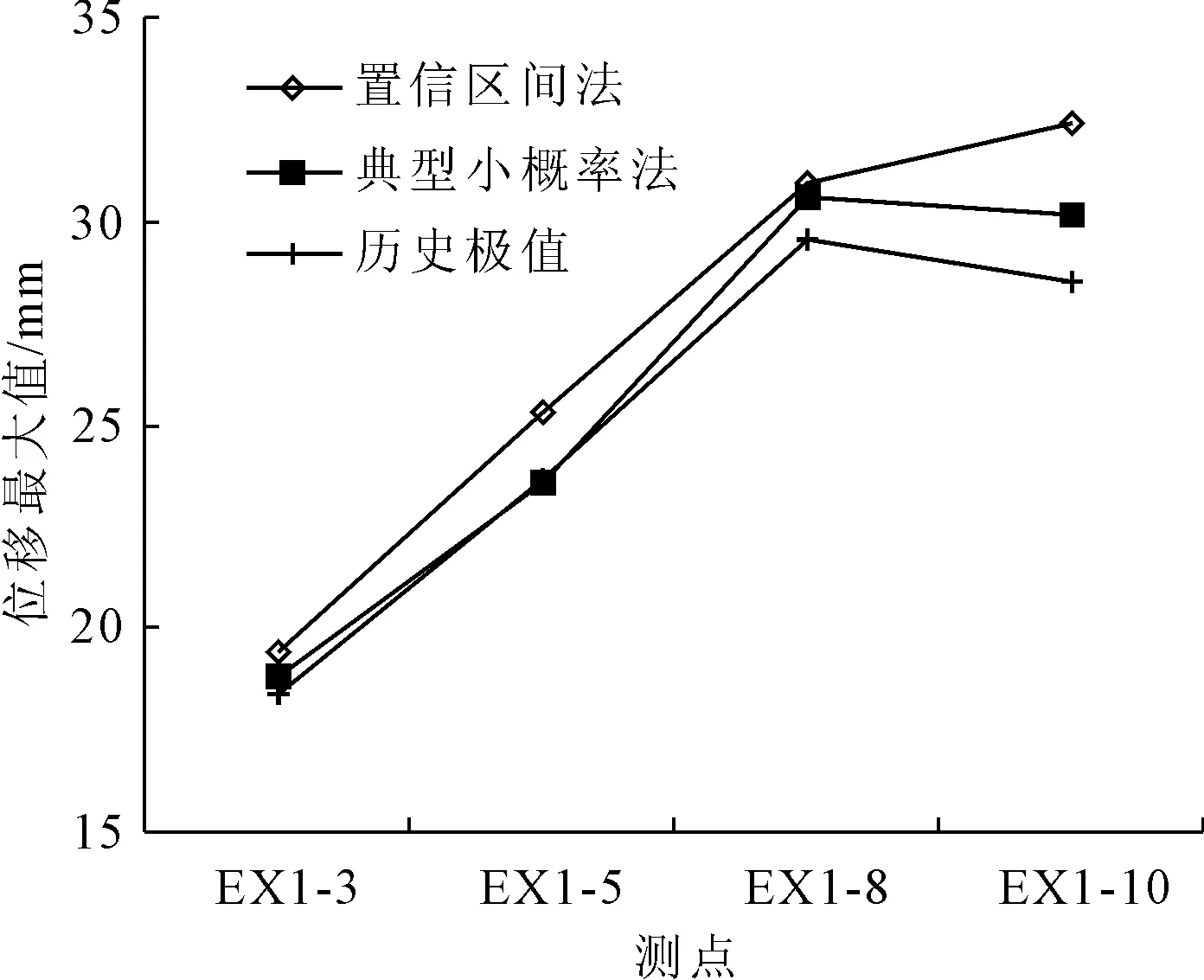
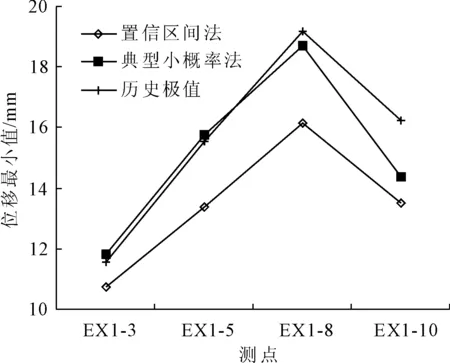
(1) 將各監測量數值排序(x1 (6) (2) 按式(7)—式(9)分別編程計算假設正態分布,對數正態分布、極值Ⅰ型分布函數的理論分布F(xk): (7) 其中μ和σ按式(2)、式(3)計算。 (8) F(xk)=exp[-exp(-a(x-u))] (9) 式中a=1.2855/σ,u=μ-0.57722/α;其中μ和σ按式(2)、式(3)計算。 (3) 用子樣的經驗分布Fn(xk)和假設的理論分布F(xk)建立統計量: Dn=max1≤k≤n{ |Fn(xk)-F(xk)|,|Fn(xk-1)-F(xk)|} (10) (4) 根據顯著性水平(取0.05),查K-S檢驗臨界值表[15],得到Dn,0.05,若Dn 根據成熟的理論模型,結合功果橋大壩的特點,其位移主要受水壓、溫度以及時效等因素的影響,考慮初始值的影響,其大壩位移的統計模型為: (11) 根據式(11)和去除粗差后的歷史觀測數據,可計算出監測效應量和原因量的數學模型,當計算精度較高時(一般要求復相關系數大于0.85),則可用該數學模型計算監控指標: (12) 取顯著水平α=5%,則β=1.96。由式(12)可計算出相應測點監測量的上下限值,如果實測值在區間內且無明顯性趨勢變化,可認為運行正常,反之是異常的。 混凝土壩體的表面變形主要受上游水深和溫度影響,一般在冬季,即上游水深較大、氣溫較低時,壩頂位移會出現向下游方向的較大值,反之,在夏季低水位時會出現向下游方向的較小值。因此,選取每年的位移最大、最小值作為典型效應量的樣本,極值統計見表1[16]。 表1 功果橋大壩典型壩段水平位移極值統計 下面以EX1-10為例進行計算說明: F(δ>δm1)= (13) 由式(13)可計算出δm1(5%的概率)的最大極值為30.175 mm。 經過K-S檢驗,引張線EX1-10的最小值滿足極值Ⅰ型分布,即δ-F(α2,μ2),其特征值α2=0.779,μ2=18.169,則δ<δm2(位移的極值)時,其概率為: (14) 由式(14)可計算出δm2(5%的概率)的最小極值為14.358 mm。 其他測點的計算結果見表2。 表2 典型小概率法計算結果 結合水位、溫度、時間歷時資料,計算出上游水位對應5%概率的水位限值。在最大值計算時,選取上游水深的上限值,計算最小值時選取上游水深的下限值。引張線監控指標置信區間法計算結果見表3。由計算結果可知,統計模型的復相關系數都在0.92以上,計算精度較高,與實測值擬合程度較好,該方法計算結果可作為綜合擬定時的依據。 以引張線EX1-3為例,統計模型的標準差S=1.118 mm,則置信區間Δ=±1.96S=±2.191 mm。該點的監控指標可用下式估計: δm=δ±2.191=7.66+0.00×(H-H0)+ 0.344×(lnθ-lnθ0)±2.191 (15) 根據引張線EX1-3的測點水位和時間歷史資料,根據式(11)和式(12)可求出水平位移的下限值10.731 mm,上限值19.422 mm。如果測值在該區間內且無明顯性趨勢變化,則認為測值正常,反之,則認為測值異常,應加強觀測和分析,查找原因,必要時采取相應的措施。 表3 置信區間法計算結果 變形項目監控指標主要從典型小概率法、置信區間估計法、時段極值三個方面進行綜合擬定,在滿足三種方法適用條件的前提下,原則上選擇上述數值中的最大或最小值,設計計算值作為參考[17]。具體擬定結果見表4和圖1、圖2。 表4 引張線監控指標綜合擬定結果 典型小概率法計算結果和歷史極值數據最為接近和吻合,置信區間法計算的最大最小值范圍相對較寬,表明大壩有繼續抵御更大荷載下的變形余量。在兩種計算結果都小于設計值的情況下,綜合擬定,主要以置信區間法的計算結果為準。 測點EX1-8位于最大河床部位壩段,從統計的歷史極值和典型小概率法計算結果來看,該測點向下游方向的位移比其他測點大,符合工程實際情況。但置信區間法的計算結果,EX1-10的位移最大值明顯大于EX1-8的位移最大值,與實際不符,故EX1-10的位移最大值綜合擬定采用典型小概率法計算結果。 圖1 三種方法確定的位移最大值分布圖 圖2 三種方法確定的位移最小值分布圖 (1) 通過統計模型的置信區間法和典型小概率法可計算大壩典型壩段的位移監控指標,并結合設計值、歷史極值對監控指標進行綜合擬定,為電廠運行管理和狀態評估提供依據。 (2) 典型小概率法計算結果和監測歷史數據最為接近和吻合,置信區間法計算的最大最小值范圍相對較寬,表明大壩有繼續抵御更大荷載下的變形余量。可結合設計值對其監控指標進行綜合擬定。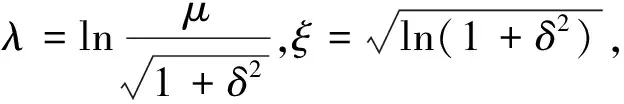
2.2 置信區間法
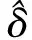
3 擬定結果
3.1 典型小概率法

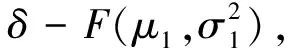
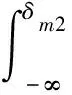
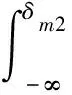
3.2 置信區間法
3.3 指標的綜合擬定
4 結 論

