曲面紋理映射算法研究及實現
王浩杰
(四川大學計算機學院,成都610065)
0 引言
紋理映射(Texture Mapping)是計算機圖形學中常用的一種技術,它被廣泛應用在3D游戲開發,虛擬現實(Virtual Reality),三維真實感圖形的生成和顯示等領域中。各種各樣復雜圖形的渲染中也使用了紋理映射技術[1]。可以將紋理映射定義為:將紋理空間中的紋理圖像映射到物體表面的過程。傳統的紋理映射算法,大多數是基于平面的,很多工業造型物體表面比如汽車、飛機、花瓶等,都是由自由曲面或不規則多邊形構成,這些物體的難以用參數表達式直接表示,因此也不能直接進行紋理映射,這也是紋理映射中的難題之一。針對這些難點,本文主要對參數曲面和不規則曲面之間的紋理映射算法進行研究。
1 紋理映射基本算法
映射(Mapping)是紋理映射中的核心問題,兩個集合中元素中間的對應關系可以用映射來表示。而紋理映射可以認為是建立兩個集合之間的映射關系。紋理空間用紋理圖像的定義域空間表示,景物空間就是需要映射的三維物體表面。紋理映射中主要包含兩個映射[2]:
假設點P1(x,y)是紋理圖像上任一點的坐標,是三維景物表面上任一點的坐標,紋理圖像到景物空間的映射就是確定三維景物表面上的點和紋理圖像上的點之間的對應關系[3],然后將紋理值賦給景物空間點,映射可以用下式表示:

景物空間到屏幕空間的映射:將景物變換為目標圖像,通過取景變換將景物顯示到屏幕上,即可得到最終的計算機圖像。
根據紋理圖像和景物空間之間的映射順序,紋理映射可以分為:正向映射、逆向映射和兩步法紋理映射。
1.1 正向映射
參數曲面紋理映射最開始采用的就是正向映射[4]的算法,也可以把它稱為紋理掃描法(Texture Scan?ning)。參數曲面紋理映射關鍵是求出目標參數曲面的逆映射,但是一般參數曲面的逆映射難以確定,最開始采用的是一種遞歸分割的方法[5],近似地建立了離散的映射關系,將紋理坐標和參數曲面坐標進行一一映射,確定紋理像素在景物參數曲面的位置和大小,再通過線性插值計算參數曲面上對應點的像素中心處的參數值。正向映射的優點是實現相對簡單,缺點是映射過程中景物參數空間和紋理空間不能完全對應。正向映射過程如圖1所示。

圖1 正向映射
1.2 逆向映射
逆向映射技術是Blinn[6]提出來的,逆向映射是一個和正向映射相反的過程,逆向映射也成被稱為屏幕掃描法(Screen Scanning)[7]。在逆向映射中,先將圖像空間中像素I所表示的區域投影到景物空間區域S,然后將S區域映射到紋理空間;這里需要對紋理圖像進行重采樣,計算曲面空間坐標中心的像素值,然后將計算結果賦值給曲面空間。逆向映射算法在一定程度上改進了正向映射的缺點,實現了紋理空間和景物參數空間的完全對應。逆向映射也是紋理映射中應用較普遍的方法之一。
2 參數曲面的紋理映射
對于一些復雜的物體,其曲面一般是非線性的,難以直接參數化,不能直接對其使用紋理映射,但是可以借助兩步法紋理映射技術[8]。其核心思想就是把原來的映射拆分為兩個映射,這個過程需要借助一個中間曲面來實現,把紋理圖像映射到簡單的中間曲面的映射記為S映射,中間曲面到最終的景物表面的映射記為O映射[9]。用O映射和S映射的復合表示完整的映射,兩步法紋理映射可以分為下面的兩個步驟:

選定一個合適的中間曲面是兩步法紋理映射的關鍵,一般來說,常見的中間曲面有球面、立方體表面、圓柱面和自由曲面,要想得到的一個比較好的紋理映射效果,選定的中間曲面需要貼近最終的目標曲面。選定中間曲面后,然后建立中間曲面到景物表面的映射關系。
2.1 二次曲面
先介紹簡單的二次曲面的紋理映射。如果可以通過一些變換把紋理空間轉換到參數空間,一些簡單二次曲面的逆映射表達式,可以直接進行紋理映射[10]。但是對于復雜的高次參數曲面來說,參數曲面的逆映射求不出解析表達式,只能通過一些數值求解算法來離散求解它們的逆映射。簡單的二次曲面,其紋理映射逆映射可以用它的解析表達式表示。
以圓柱面為中間曲面的參數表示,一個高為h,半徑為r的圓柱面的參數表達式為:


以圓柱面為中間曲面的紋理映射的原理如圖2所示:
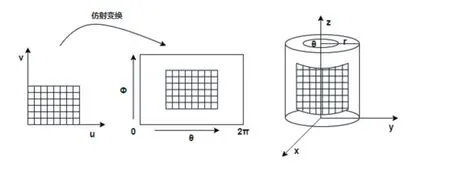
圖2 柱面映射
2.2 Bezier曲面
常用的自由曲面有Bezier曲面[11]和B樣條曲面,它們可以靈活的控制曲面的形狀。基于控制點實現的自由曲面控制靈活,方便造型,易于拼接。參數曲面的解析表達式就是二維參數空間到三維空間的映射,利用其解析表達式能夠方便實現紋理映射。
Bezier曲面的定義如下:設Pij(i=0,1,…,m;j=0,1,…,n)為( )m+1×(n+1)個控制點列,則m×n次Bezier曲面定義為:


其中Pij是控制點,是Bernstein基函數。當n=m=3時,得到的雙三次Bezier曲面如下:

矩陣形式如下:
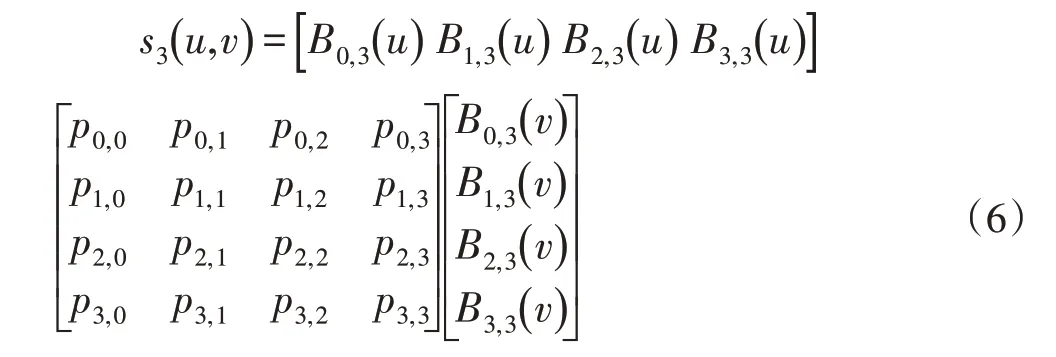
Pij(i=0,1,2,3;j=0,1,2,3)構成了參數曲面的控制點矩陣,一張雙三次Bezier曲面片由16個控制點確定。由Pij組成的空間網格稱為特征網格,曲面的形狀受到特征網格中控制頂點的控制,通過調節控制頂點,曲面的形狀也隨之改變。雙三次Bezier曲面如圖3所示:

圖3 雙三次Bezier曲面
2.2 NURBS曲面
在計算機中,很多曲線和曲面都可以通過樣條曲線等參數曲線來描述。其中,B樣條(B-Spline)在工業設計中的應用十分廣泛[12]。k次B樣條曲線的表達式如下:


其中ti為節點值構成了樣條曲線的節點矢量矩陣。
3D設計中經常包括NURBS(Non-Uniform Ratio?nal B-Spline),非均勻有理B樣條曲線是一個分段的有理多項式函數,其定義如下:
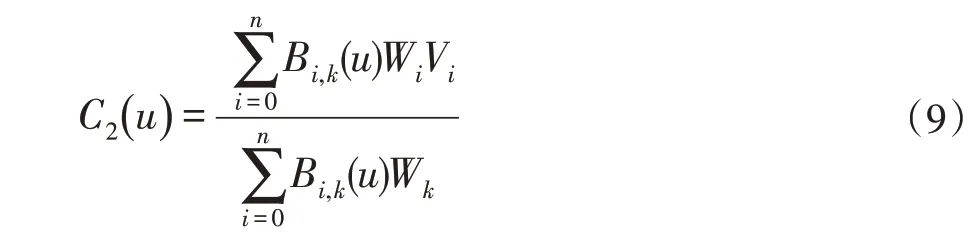

其中k為冪次,ui(i=0,1,…,m)為節點,當冪次=k,控制點數=n+1,節點數=m+1時,可以得到m=n+1。
三維NURBS曲面的定義如下:


定義樣條曲線的求值器P(u),且u∈[0,1],表達式如下:

其中Pi表示控制點,如果u的取值范圍為,求值器的值為:

對于二維曲面,求值器的表達式為:

一般來說,實際使用的NURBS曲面和Bezier曲面都少于4次,常用的是3次曲面。B樣條曲面和Bezier曲面都可以通過調整控制點來控制曲面的形狀,造型能力很強。通過OpenGL實現的NURBS曲面如圖4所示:

圖4 NURBS曲面
3 紋理映射的實現
紋理映射實現就是將一張紋理圖像貼到三維物體表面,就像貼墻紙一樣。下面介紹曲面紋理映射的實現過程。
3.1 紋理映射的實現步驟
紋理映射的實現過程主要包括下面的一些步驟:紋理定義、紋理控制、確定映射方式和紋理坐標的確定。
(1)創建紋理:
創建一個紋理對象,并將它和紋理單元進行綁定。或者直接讀取已知的紋理圖像,然后綁定,一般情況下紋理認為是二維的。
(2)建立映射函數:
映射函數用來表示紋理坐標和三維物體坐標之間的對應關系,有參數表達式的曲面,可以直接利用它們的參數表達式。有時候也需要利用中間曲面,就是建立到中間曲面的映射函數。不同的物體之間的映射函數不一樣,需要建立一個頂點之間的映射關系。
(3)設置映射方式:
設置紋理映射的顏色參數,有時可以直接將紋理圖像作為顏色映射到曲面上,紋理就好像被粘貼在曲面上;如果想得到比較好的光照和紋理綜合效果,把景物曲面的顏色或顏色比例和紋理圖像的紋理值結合,通過紋理值來靈活調整;還可以采用一種混合的方式:把曲面原來的顏色和一個固定顏色紋理值進行混合。
(4)激活紋理映射:
先對紋理進行處理:與指定顏色和法向量類似,需要為每一個頂點分配紋理坐標。在最終的繪制之前,需要激活紋理映射。
(5)繪制幾何場景:
在進行最后的映射之前,需要了解紋理相對于曲面是怎么排列的,必須指定場景中物體的紋理坐標和幾何坐標。經過幾何變換之后頂點在屏幕上繪制的位置是由幾何坐標決定的,而紋理坐標決定紋理圖像中哪個紋理像素值賦值給該頂點。
3.2 實驗結果
實驗以VC++2013為編程環境,利用OpenGL對紋理映射技術進行研究和驗證。通過OpenGL實現了曲面紋理映射,圖4展示了把一個帶狀紋理映射到茶壺表面的效果圖;Bezier曲面的紋理映射效果如圖5所示:將一個棋盤紋理圖像映射到雙三次Bezier曲面上。

圖5茶壺曲面紋理映射

圖6 Bezier曲面上的紋理映射
4 結語
本文通過研究曲面紋理映射算法,對經典的紋理映射算法進行了總結和分析;結合兩步法紋理映射技術,研究了自由曲面和參數曲面中的紋理映射算法;并利用OpenGL實現了參數曲面紋理映射算法,以及對相關的曲面紋理映射技術進行了驗證。實驗結果表明,這些紋理映射算法中可能會產生反走樣現象,這個問題還沒有很好地解決,還需要深入研究,后續將著重研究如何減少映射過程中的反走樣現象,這些研究內容對紋理映射的應用有重要意義。

