自適應抗差卡爾曼濾波對井下定位NLOS時延抑制方法的研究

李康樂 邵小強 潘紅光 郭德鋒 鄭潤洋 衛晉陽

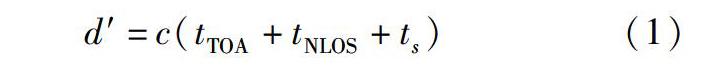
摘?要：針對礦井巷道NLOS（Non Line Of Sight）時延影響礦井TOA（Time Of Arrival）定位精度的問題，通過分析巷道NLOS時延形成方式，將巷道NLOS時延分為隨機和固定兩類，結合兩類巷道NLSO時延的特性，提出了一種基于自適應抗差卡爾曼濾波的巷道NLOS時延抑制方法。對于巷道隨機NLOS時延，通過在經典卡爾曼濾波算法的基礎上引入了自適應抗差概念，使系統在線性濾波的基礎上增加了對隨機脈沖誤差的抑制能力;對于巷道固定NLOS時延，通過在巷道NLOS誤差模型的基礎上，構建巷道中信號傳播距離與傳播環境間的函數模型，并結合幾何定位算法完成系統對固有誤差的有效抑制。實驗結果顯示，包含有巷道NLOS時延的原始定位數據，誤差在2.1～8.1 m之間，平均誤差為3.7 m;原始數據經自適應抗差卡爾曼濾波算法處理后，誤差在1.9～3.6 m之間，平均誤差為2.5 m，定位曲線與實際移動曲線基本保持平行;再經參數擬合和幾何算法處理，誤差在0～1.0 m之間波動，誤差平均值為0.27 m，且所提方法較原始定位數據，平均定位誤差減小了3.43 m.從而表明，所提方法對巷道NLOS時延具有較明顯的抑制作用，能夠提高TOA井下人員定位系統的精確度。

關鍵詞：礦井定位;NLOS;自適應抗差卡爾曼濾波;參數擬合;TOA

中圖分類號：TD 76

文獻標志碼：A

文章編號：1672-9315（2020）01-0173-08

DOI：10.13800/j.cnki.xakjdxxb.2020.0123開放科學（資源服務）標識碼（OSID）：

Downhole positioning NLOS delay suppression

method

based on adaptive robust Kalman filter

LI Kang-le，SHAO Xiao-qiang，PAN Hong-guang，GUO De-feng，ZHANG Run-yang，WEI Jin-yang

（College of Electric and Control Engineering，Xian University of Science and Technology，Xian 710054，China）

Abstract：To solve the problem that the positioning accuracy of time of arrival（TOA） positioning method is susceptible to delay of the non line of sight（NLOS），and based on the analysis of the formation mode of mine roadway，the NLOS delay of the roadway was divided into random NLOS delay and fixed NLOS delay.Taking the characteristics of two kinds of NLOS delays into consideration，a method of mine TOA positioning based on improved Kalman filter and parameter fitting is proposed.In order to eliminate the random NLOS delay error in roadway，the concept of adaptively robust was introduced to the basis of the classical Kalman filter algorithm.On the basis of linear filtering，the system can suppress random impulse error.Meanwhile，in order to suppress the fixed NLOS delay error，the roadway range finding error model was proposed，in which the functional relationship between signal propagation distance and propagation environment was established.Thus，the inherent error can be reduced by using the geometric positioning algorithm.The simulation results indicate that the original positioning data containing the NLOS delay of the roadway has an error between 2.1 and 8.1 m and an average error of 3.7 m.After the measurement data was processed by the Kalman filter based on the threshold of innovation，the positioning error is kept between 1.9 and 3.1 m and an average error of 2.5 m，and the positioning curve is basically parallel to the actual movement curve.After being processed by the parameter fitting and geometric algorithm，the positioning error is between 0 and 1.0 m，and the average error is 0.27 m.By comparison with the original positioning data，the average positioning error of the proposed method is reduced by 3.43 m.It can be found that the proposed method has a prominent inhibitory effect on the NLOS delay，and has a great effect on improving the accuracy of TOA downhole crew positioning system.

Key words：mine positioning;NLOS;adaptive robust Kalman filter;parameter fitting;TOA

0?引?言

中國煤礦90%以上是地下煤礦，且隨著煤礦采區的不斷擴大和作業巷井的不斷加深，對井下作業人員和設備的監控管理日益困難，而現有煤礦井下人員定位系統的定位精度無法達到當前數字礦井建設的要求[1-3]。所以，建設煤礦井下人員精確定位系統是煤礦正常生產、調度、災害救援等工作的首要任務。

基于測距的井下定位技術是當前礦井定位的主要手段[4-5]。礦井TOA （Time Of Arrive）是一種基于信號到達時間的井下精確定位技術，在井下定位系統中有著廣泛的應用[6-8]。但由于煤礦井下通信空間受限，對無線信號的傳輸形成了巨大干擾，同時又無法應用GPS時間同步方式實現時鐘同步，因此形成的計時誤差、同步時延和NLOS時延等會對TOA定位精度產生無法忽略的影響。

針對當前煤礦定位精度不能滿足井下物聯網建設的需求，孫繼平等提出了一種采用單路光纖道+雙路WiFi信道的計時誤差抑制方法，有效消除了礦井定位中的計時誤差和同步時延，但并未對巷道NLOS時延對TOA定位的影響進行分析[9]。針對礦井定位系統可靠性較差的問題，劉真真等提出了一種基于指紋定位的井下分布式目標定位方法，對定位系統的實時性和可靠性均有明顯提升，但并未對巷道電磁波NLOS傳播時延起到明顯的抑制作用[10]。

在采用SDS-TWR方法抑制計時誤差和同步時延的基礎上，孫繼平等提出了一種基于均值濾波算法和參數擬合的巷道NLOS時延方法。該方法依據圖像濾波原理，將均值濾波應用到礦井定位中，一定程度上抑制了巷道隨機NLOS時延，但不能完全消除，測量結果仍存在較大的偏差[11]。以TOA定位中存在的巷道NLOS時延為研究對象，通過分析NLOS時延的特性，孫繼平等提出了基于TOA的井下指紋定位算法。該算法借助井下定位基站，對礦井巷道中各個區域進行位置信息采集，并將位置信息按照統一的存儲協議上傳到定位服務器中，完成井下位置指紋數據庫的建立[12]。從而根據指紋定位算法的原理實現井下人員定位，但該算法處理后的定位誤差波動較大，平均定位誤差為0.7 m，無法滿足當前煤礦對井下人員定位的需求。

在采用SDS-TWR方法的基礎上，通過詳細分析巷道NLOS時延的分類和特點，提出了一種基于改進卡爾曼濾波的巷道NLOS時延抑制方法。

1?巷道NLOS時延分析

基于TOA的測距技術在采用SDS-TWR方法測得的距離數據中，包含了巷道NLOS時延誤差和系統設備的測量誤差。測量值的表達式為

式中?tTOA為信號傳播的實際值;ts為定位系統的觀測誤差;tNLOS為巷道NLOS造成的時延;c為光速。在采用SDS-TWR方法時，ts很小，對TOA測量值的影響可以忽略，所以巷道NLOS時延是當前影響TOA定位精度的主要因素。

1.1?巷道NLOS時延分類

電磁波在巷道傳輸過程中，由于障礙物的存在，致使信號無法通過直線等最短路徑在發送設備和接收設備間傳輸的一種現象，稱為巷道電磁波的NLOS傳播[13-14]。所以在應用礦井TOA定位時，TOA測量值中必然存在電磁波NLOS傳播所引起的時延誤差。

一方面，巷道中的電氣控制設備、消防設施以及通信電纜等固定設備設施導致電磁波在井下無法按照直射徑傳播，從而產生巷道NLOS時延。但是由于這些設備在相同巷道內，設備數量和布置密度基本一致，且具有相對固定性，從而導致其產生的巷道NLOS時延較為平穩。

通過對電磁波傳播過程的研究，得出了電磁波NLOS傳播模型[15]。在文獻[15]研究的基礎上，結合礦井巷道NLOS時延的特點，SU等提出了一種基于礦井巷道的電磁波NLOS傳播模型[16]，即

tNLOS=Tτdθξ

（2）

式中?Tτ為信號傳輸間距等于1 km時的中值，是已知固定參數;ξ為隨機變量，且服從對數分布的;d為信號傳輸的距離;θ為0～1之間的指數。

通過對井下固定設施的安裝密度、更新頻率以及對無線信號傳輸的影響等因素的綜合分析，提出了一種適用于井下巷道的NLOS傳播模型[17]。在該模型的基礎上，假定tNLOS：E（λ），則有

式中?E（tNLOS）為tNLOS的均值;

D（tNLOS）為tNLOS的方差;mz，σz為z=10logξ的均值與均方差，其中z服從高斯分布;d為距離。通過式（3）和（4）發現，電磁波在僅有固定設備的礦井巷道中傳輸的實際距離與理論值之間的關系相對穩定，即由此產生的NLOS時延誤差也較為恒定，故而將其稱為巷道固定NLOS時延。

另一方面，井下無線信號傳輸環境的穩定性易被具有不確定性的機車等移動設備打破。通過研究隨機性設備對無線信號傳輸環境的影響，

發現不確定性設備對無線信號傳輸環境的影響是巨大的，且不易于量化分析[18]。所以把由機車等不

確定性設備造成的時延誤差稱之為隨機NLOS時延。

1.2?巷道NLOS時延誤差特點

根據電磁波非直射徑傳播的特性發現，電磁波NLOS傳播均造成正向誤差，即井下定位時，測量值較實際值明顯偏大。由于2類巷道NLOS時延是由不同井下設備引起，所以它們對定位精度的影響也不同。根據電磁波似光理論和費馬原理分析發現，無線信號傳輸時，總是以環境最優路徑傳輸[19]。

對于巷道固定NLOS時延，假定定位基站到井下作業人員間的最短距離為l，且巷道中不存在機車等移動設備，即在巷道固定NLOS環境下。假定無線信號直線傳輸的距離為l′，m為傳輸過程中的路徑改變的次數，故有

從而表明，在巷道固定NLOS時延環境下，無線信號傳輸過程路徑的改變次數和傳輸距離是影響定位誤差的主要因素，且定位誤差Δd的大小與傳輸距離l′，路徑改變的次數m成正比。同時，由于井下固定設施布置密度基本一致，導致其引起的巷道固定NLOS時延具有規律性。

對于巷道隨機NLOS時延，由于井下機車等不確定性設備體型較大，且移動速度變化較快，在巷道中出現會迫使巷道無線信號傳輸環境的由穩定期轉入震蕩期，致使信號傳輸時間產生一個較大增量，因此其引起的巷道NLOS時延具有顯著性、不確定性等明顯特點。

綜上所述，基于TOA的礦井巷道NLOS時延可以分為具有隨機性、顯著性和難以定量分析等特點的巷道隨機NLOS時延和具有穩定性、規律性等特點的巷道固定NLOS時延2類。所以需要針對不同巷道NLOS時延的特性研究對應的抑制方法。

2?改進卡爾曼濾波算法

2.1?經典卡爾曼濾波算法

經典卡爾曼濾波算法的基礎動態系統通常用狀態空間模型進行描述，其中狀態空間模型主要由狀態方程和觀測方程組成[20-25]，即

式中?k為離散時間;X（k）∈Rn為k時刻的狀態值;

Y（k）∈Rm為k時刻的觀測值;Φ為狀態轉移矩陣;H為觀測矩陣;

W（k）∈Rr為輸入的白噪聲;

V（k）∈Rm為觀測噪聲。

若假設

W（k）和V（k）為不相關白噪聲，且均值均為零，方差陣分別為Q和R，則

式中?X（j）為j某時刻的狀態量;

（j|k）為X（j）的線性最小方差估計值。

在卡爾曼濾波算法的系統式（7）和式（8）以及上面假設下，可得到卡爾曼濾波的遞推過程如下

X（k）為k時刻狀態量的估計值和預測值;

（k）和P（k）為k時刻狀態變量估計誤差和預測誤差的協方差矩陣;K（k）為k時刻的Kalman增益;ε（k）為測量矩陣

Y（k）的新息值。

經典卡爾曼濾波算法對線性系統具有出色的濾波能力，但對于存在顯著性脈沖誤差的非線性系統，濾波能力會大打折扣。因此，本文針對巷道隨機NLOS時延的特點，將自適應抗差的概念引入經典卡爾曼濾波中，形成了一種能夠對隨機性誤差有效抑制的卡爾曼濾波算法。

2.2?自適應抗差卡爾曼濾波算法

自適應抗差卡爾曼濾波算法的基礎理論和遞推過程與經典卡爾曼濾波算法一致。

在經典卡爾曼濾波算法中，新息向量

ε（k）=Y（k）-H（k），其協方差矩陣為

D（k）=HP（k）HT

（23）

假設井下電磁波傳播環境為LOS環境，即巷道中沒有引起電磁波NLOS傳播的設備時，則有ε（k）～N（0，σ2）;反之，則ε（k）～N（Y（k）-（k），σ2），（k）為TOA的標準測量距離，則檢驗信息為

若利用式（24）作為判斷TOA測量環境的依據，則有

式中?r為閾值，用于區分LOS環境和NLOS環境，需在LOS環境下，針對不同類型的巷道和影響因素，通過多次TOA測距實驗來確定。在式（25）的基礎上，利用Huber函數得

用式（26）中的

（k）代替式（20）中的

R（k），便可以使改進后的卡爾曼濾波算法具有了自適應特性，能夠針對不同類型誤差提供匹配的抗差更新值，從而使其不僅能夠抑制線性誤差，也能對隨機性脈沖誤差進行有效抑制。所以，自適應抗差卡爾曼濾波算法能夠實現對巷道隨機NLOS時延的有效抑制。

3?基于參數擬合的幾何定位算法

TOA定位通常采用雙定位基站估計移動目標的位置，假設d為兩基站間的距離。由于自適應抗差卡爾曼濾波算法只能抑制巷道隨機NLOS時延，對巷道固定NLOS時延沒有明顯的抑制作用，所以導致測量數據存在明顯的正向誤差，如圖1所示。

由于相同巷道固定設備設施布置相同，所以相同巷道中不同基站測試數據所包含的巷道固定NLOS時延相同。因此結合式（1）和式（2）有

式中?d′1和d′2分別為只含有巷道固定NLOS時延的測量值;d1和d2分別為定位的實際值。假設p為巷道NLOS時延系數，則有

因為式（29）中p和θ未知，所以需要在無隨機因素影響的巷道中測取基站到任意m點的d′和d，建立二元方程組，進而通過參數擬合求解未知量。假設巷道任意點與基站1的實際距離為d1（1），d1（2），…，d1（m），測量距離為d′1（1），d′1（2），…，d′1（m），進而有

運用參數擬合求解式（30），選擇解集中具有最小歐氏距離的一組數值解作為

p和θ的參數擬合值。因此，對應的抑制巷道固定NLOS時延的計算公式為

由于文中定位方法假定礦井巷道為一維直線，但實際巷道為二維平面，從而導致定位結果存在漂移。所以需要運用幾何算法對測量位置進行歸一化處理，即

式中?1和2分別為歸一化處理后定位目標與基站1和基站2的距離，m.

4?仿真分析

4.1?仿真方法及流程

礦井巷道結構和井下定位基站分布如圖2所示。井下巷道分布主要有帶狀和條狀2種形式，且具有分支，定位基站按照巷道的實際走向，采用直線方式安裝，基站配備有檢測信號方向的雙向定向天線，且均安裝在巷道頂板中點這個最佳安裝位置，相鄰兩個基站距離固定。攜帶有定位識別卡的井下作業人員在礦井巷道中正常工作，機車等運輸設施在巷道中按照既定路線運輸。定位方法的工作流程如下

1）定位基站以固定的采樣時間向定位區域發送人員檢測信號，一旦檢測到人員定位卡，基站記錄信號到達時間，并進行再次檢測。

2）基站通過信號傳輸電纜，將記錄的時間值、定位卡編號和基站編號等信息傳回地面服務器。

3）服務器通過識別卡編號讀取基站檢測的時間值，并通過自適應抗差卡爾曼濾波算法對時間值進行處理，之后根據式（1）將時間轉化為距離值。

4）服務器根據基站編號，匹配相應的巷道參數，進而運用參數擬合和幾何定位算法對距離值進行處理，得到人員定位卡與該基站的距離估計值。

5）服務器選取相鄰基站的距離值作為該定位卡在巷道中的坐標值，并結合基站在巷道中的位置，輸出定位卡在巷道中的實際位置。

4.2?仿真結果分析

在文獻[26]測試環境和測試數據的基礎上，運用MATLAB建立自適應抗差卡爾曼濾波、參數擬合和幾何算法的模型對測試數據進行仿真分析。其中測試環境如圖2所示，相鄰基站相距60 m，作業人員以1.5 m/s的速度在巷道勻速移動，

運動方向是從基站1到基站2.仿真原始數據見表1.

以表1中的實際位置和SDS-TWR測量位置作為算法原始輸入數據，并結合式（7）和式（8）建立卡爾曼濾波狀態空間模型。然后經抗差矩陣閾值r=2的自適應抗差卡爾曼濾波算法處理，得到如表1所示的自適應抗差卡爾曼濾波算法估計位置。在自適應抗差卡爾曼濾波算法的基礎上通過參數擬合求得巷道NLOS時延系數p=2.653 7和指數θ=0.012 1，再經幾何算法處理得到如表1所示的所提算法的估計位置，文中所提方法的定位曲線如圖3所示，誤差曲線如圖4所示。

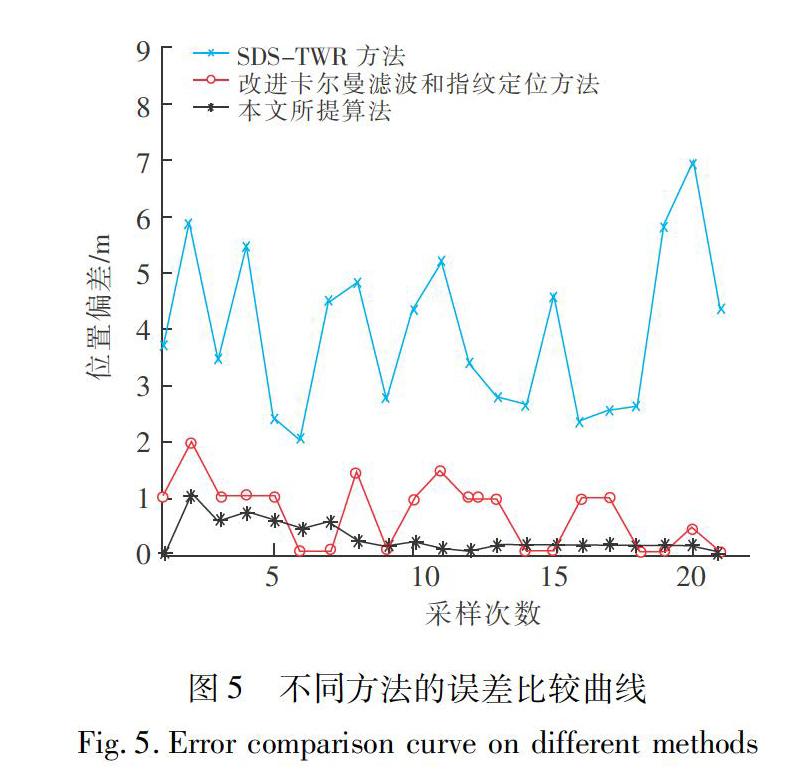
從表1和圖3，圖4可以看出，采用SDS-TWR方法直接測的原始數據誤差范圍為2.1～8.1 m，平均誤差為3.7 m，包含有巷道隨機NLOS時延誤差和巷道固定NLOS時延誤差;數據經過自適應抗差卡爾曼濾波算法處理后誤差在1.9～3.6 m之間，平均誤差為2.5 m，即基本上消除了巷道隨機NLOS時延誤差，但還存在巷道固定NLOS時延誤差;經過參數擬合和幾何算法處理后的數據誤差范圍為0～1 m，平均誤差降為0.27 m，表明巷道NLOS時延誤差基本消除。不同方法的誤差比較曲線如圖5所示。

通過表1和圖5分析發現，若不經任何巷道NLOS時延抑制算法處理，直接采用SDS-TWR方法測得的定位結果誤差在2.1～7.0 m之間波動，誤差平均值為3.9m;當在SDS-TWR方法的基礎上經卡爾曼濾波和指紋定位算法處理，得到消除巷道NLOS時延的定位結果，誤差在0～2.0 m之間波動，誤差平均值為0.7 m;當在SDS-TWR方法的基礎上經所提方法處理，得到抑制巷道NLOS時延誤的定位結果，誤差在0～1.0 m之間波動，誤差平均值為0.27 m.相比于前面兩種方法，文中所提方法的定位誤差平均值減小了3.63和0.43 m.因此表明，所提方法對巷道NLOS時延有明顯的抑制作用，且定位誤差明顯小于其他定位方法。

5?結?論

1）巷道NLOS時延分為隨機和固定兩類，其中隨機時延具有隨機性、顯著性和難以定量分析等特點，固定時延具有相對穩定性和規律性等特點。

2）自適應抗差卡爾曼濾波算法能夠有效抑制巷道隨機NLOS時延，但對固定時延沒有明顯的抑制作用，算法的性能取決于抗差矩陣閾值的選擇。

3） 參數擬合和幾何定位算法能夠明顯抑制巷道固定NLOS時延，且定位結果較為準確，但參數擬合值需要根據不同巷道環境進行選取。

4） 經仿真驗證，所提方法對巷道NLOS時延有較明顯的抑制作用，定位精度有較大提升，可以滿足礦井TOA定位在井下NLOS環境中的應用。

參考文獻（References）：

[1]申?雪，劉?馳，孔?寧，等.智慧礦山物聯網技術發展現狀研究[J].中國礦業，2018，27（7）：120-125，143.SHEN Xue，LIU Chi，KONG Ning，et al.Research on the technical development status of the intelligent mine base on internet of things[J].China Mining Magazine，2018，27（7）：120-125，143.

[2]霍振龍.礦井定位技術現狀和發展趨勢[J].工礦自動化，2018，44（2）：51-55.HUO Zhen-long.Status and development trend of mine positioning technology[J].Industry and Mine Automation，2018，44（2）：51-55.

[3]胡青松，張?申，吳立新，等.礦井動目標定位：挑戰、現狀與趨勢[J].煤炭學報，2016，41（05）：1059-1068.HU Qing-song，ZHANG Shen，WU Li-xin，et al.Localization techniques of mobile objects in coal mines：challenges，solutions and trends[J].Journal of China Coal Society，2016，41（5）：1059-1068.

[4]劉世森.基于AOA的礦井人員精確定位技術[J].煤礦安全，2019，50（7）：140-142，146.LIU Shi-sen.Accurate positioning technology for mine workers based on AOA[J].Safety in Coal Mine，2019，50（7）：140-142，146.

[5]孫哲星，孫繼平.異步測時礦井人員精確定位方法[J].煤炭學報，2018，43（5）：1464-1470.SUN Zhe-xing，SUN Ji-ping.Underground coal mine accurate personnel positioning method based on asynchronous time-measuring[J].Journal of China Coal Society，2018，43（5）：1464-1470.

[6]Khan U H，Rasheed H，Aslam B，et al.Localization of compact circularly polarized RFID tag using TOA technique[J].Radio engineering，2017，26（1）：147-153.

[7]Shao Xiao-qiang，Li Kang-le，Chen Xi.A method of TOA positioning for mine to effectively reduce the impact of Non-Line of sight error propagation[C]//Proceedings of the 30th Chinese Control and Decision Conference，CCDC 2018.Shenyang：Institute of Electrical and Electronics Engineers Inc.，2018：4650-4655.

[8]ZHANG Rui，XIA Wei-wei，YAN Feng，et al.A single-site positioning method based on TOA and DOA estimation using virtual stations in NLOS environment[J].China Communications，2019，16（2）：146-159.

[9]孫繼平，李晨鑫.基于WiFi和計時誤差抑制的TOA煤礦井下目標定位方法[J].煤炭學報，2014，39（1）：192-197.

SUN Ji-ping，LI Chen-xin.TOA underground coal mine target positioning method based on WiFi and timing error suppression[J].Journal of China Coal Society，2014，39（1）：192-197.

[10]劉真真，田子建，王文清，等.基于TOA壓縮感知的礦井分布式目標定位方法[J].煤炭科學技術，2018，46（9）：188-195.LIU Zhen-zhen，TIAN Zi-jian，WANG Wen-qing，et al.Mine distributed target location method based on TOA compressed sensing[J].Coal Science and Technology，2018，46（9）：188-195.

[11]孫繼平，李晨鑫.基于改進均值濾波和參數擬合的礦井TOA幾何定位方法[J].煤炭學報，2015，40（5）：1206-1212.SUN Ji-ping，LI Chen-xin.Mine TOA geometric positioning method based on improved mean filtering and parameter fitting[J].Journal of China Coal Society，2015，40（5）：1206-1212.

[12]孫繼平，李晨鑫.基于卡爾曼濾波和指紋定位的礦井TOA定位方法[J].中國礦業大學學報，2014，43（6）：1127-1133.SUN Ji-ping，LI Chen-xin.Mine time of arrival positioning method based on Kalman filtering and fingerprint positioning[J].Journal of China University of Mining & Technology，2014，43（6）：1127-1133.

[13]Korrai P K，Rao K D.Performance analysis of downlink mmWave networks under LOS/NLOS propagation with blockage and directional beamforming[J].Telecommunication Systems，2019，72（1）：53-68.

[14]李旭虹，張同麗，張育芝.礦井NLOS環境下改進UKF超寬帶定位算法[J].西安科技大學學報，2018，38（5）：824-829.LI Xu-hong，ZHANG Tong-li，ZHANG Yu-zhi.Research on improved UKF UWB localization algorithm in mine NLOS environment[J].Journal of Xian University of Science and Technology，2018，38（5）：824-829.

[15]CHENG Long，WANG Yan，SUN Xing-ming，et al.A mobile localization strategy for wireless sensor network in NLOS conditions[J].China Communications，2016，13（10）：69-78.

[16]SU Zheng-qiang，SHAO Gen-fu，LIU Hua-ping.Semidefinite programming for NLOS error mitigation in TDOA localization[J].IEEE Communications Letters，2017，21（09）：15-34.

[17]曾?玲，彭?程，劉?恒.基于非視距鑒別的超寬帶室內定位算法[J].計算機應用，2018，38（S1）：131-134，139.ZENG Ling，PENG Cheng，LIU Heng.UWB indoor positioning algorithm based on NLOS identification[J].Journal of Computer Applications，2018，38（S1）：131-134，139.

[18]黃越洋，張嗣瀛，井元偉，等.基于TDOA和RSS的可行域粒子濾波非視距定位算法[J].控制與決策，2017，32（8）：1415-1420.HUANG Yue-yang，ZHANG Si-ying，JING Yuan-wei，et al.Non-line of sight localization algorithm based on TDOA and RSS by feasible region particle filter[J].Control and Decision，2017，32（8）：1415-1420.

[19]鮑小雨，王?慶，陽?媛，等.一種抑制NLOS誤差的UWB定位方法[J].傳感器與微系統，2019，38（9）：9-12.BAO Xiao-yu，WANG Qing，YANG Yuan，et al.A UWB positioning method for suppressing NLOS error[J].Transducer and Microsystem Technologies，2019，38（9）：9-12.

[20]周?瑞，袁興中，黃一鳴.基于卡爾曼濾波的WiFi-PDR融合室內定位[J].電子科技大學學報，2016，45（3）：399-404.ZHOU Rui，YUAN Xing-zhong，HUANG Yi-ming.WiFi-PDR fused indoor positioning based on Kalman filtering[J].Journal of University of Electronic Science and Technology of China，2016，45（3）：399-404.

[21]ZHOU Cheng，YUAN Jia-zheng，LIU Hong-zhe，et al.Bluetooth indoor positioning based on RSSI and Kalman filter[J].Wireless Personal Communications，2017，96（3）：4115-4130.

[22]ZHU Da-li，ZHAO Bo-bai，WANG Si-ye.Mobile target indoor tracking based on multi-direction weight position Kalman filter[J].Computer Networks，2018，141：115-127.

[23]SONG Dong-ran，YANG Jian，DONG Mi，et al.Kalman filter-based wind speed estimation for wind turbine control[J].International Journal of Control Automation & Systems，2017，15（3）：1089-1096.

[24]周?牧，耿小龍，謝良波，等.室內WiFi/PDR自適應魯棒卡爾曼濾波融合定位方法[J].電子學報，2019，47（1）：9-15.ZHOU Mu，GENG Xiao-long，XIE Liang-bo，et al.Indoor WiFi /PDR fusion localization based on adaptive and robust Kalman filter[J].Acta Electronica Sinica，2019，47（1）：9-15.

[25]孫?偉，段順利，閆慧芳，等.基于卡爾曼平滑的AWKNN室內定位方法[J].電子科技大學學報，2018，47（6）：829-833.SUN Wei，DUAN Shun-li，YAN Hui-fang，et al.AWKNN indoor location methods based on Kalman smoothing[J].Journal of University of Electronic Science and Technology of China，2018，47（6）：829-833.

[26]邵小強，李康樂，陳?熙，等.基于改進卡爾曼濾波和參數擬合的礦井TOA定位方法[J].煤炭學報，2019，44（5）：1616-1624.SHAO Xiao-qiang，LI Kang-le，CHEN Xi，et al.TOA positioning method of coalmine based on Kalman filter and parameter fitting[J].Journal of China Coal Society，2019，44（5）：1616-1624.