第一性原理計算Cu、Co含量對 CoCuFeNi系高熵合金的影響*

王 根，李新梅

(新疆大學 機械工程學院,烏魯木齊 830047)

0 引 言

高熵合金(high-e-entropy alloys,HEAs)是由臺灣學者葉鈞蔚在20世紀90年代在傳統合金的研究基礎之上提出的一種新的合金設計理念[1]。高熵合金與傳統合金的最大區別在于其組元的含量在5%～35%(原子比)之間，組元的個數為4個或更多[2]。這種多組元合金并未形成復雜的化合物，相反主要是形成了簡單的固溶體相，且合金表現出優異的性能[3]。這些特性引起了許多學者和專家的注意，并對這類多主元合金進行了大量的研究。隨著對高熵合金的不斷深入研究，科研人員提出了高熵合金的四大效應——高熵效應、晶格畸變效應、遲滯擴散效應和“雞尾酒”效應[2]。吳炳勇[2]采用機械合金化法和放電等離子燒結制備了FeNiCoCu系高熵合金，研究了不同元素的添加對其組織與性能的影響，結果表明該類高熵合金具有優異的塑性，隨Cu含量的逐漸增加，合金的強度不斷提高；郭亞雄等[4]采用激光熔覆技術制備了高熔點的AlCrFeMoNbxTiW涂層，研究了該類高熵合金的微觀組織與耐磨性能，研究表明隨Nb含量的增大，涂層的硬度升高，耐磨損性能提高，涂層的磨損機理是以磨粒磨損為主。

近些年，隨著對高熵合金研究的不斷深入，通過實驗建立高熵合金中主要元素對合金性能影響的規律與機制，不僅工作量較大，而且存在較大的不確定性，基于密度泛函數理論的第一性原理計算可以很好地解決這些問題。通過計算，可以從原子、分子層面來討論材料的顯微結構和性能。Z.S.Nong等[5]利用第一性原理計算，研究了FeTiCoNiVCrMnCuAl系高熵合金體系中常見金屬間化合物的結構電子和彈性性能，研究了其對高熵合金性能的影響，結果表明，由于FeTi、Fe2Ti、AlCrFe2、Co2Ti、AlMn2TiV及Mn2Ti等相的形成焓<-0.35 eV/atom、內聚能<-7.0 eV/atom，結構較為穩定，通過計算金屬間化合物力學性能發現其可以進一步提升高熵合金的硬度，并通過對化合物進行DOS計算，研究了金屬間化合物的成鍵能力；S.P.Wang等[6]利用第一性原理計算方法，對FeNiCrCuCo高熵合金的結構和力學性能進行了研究，結果表明，Cr的加入增加了高熵合金的生成焓，降低了晶格常數。

Co、Cu、Fe和Ni 4種元素在元素周期表中位置相鄰，Co、Fe和Ni 3種元素制備的合金能夠形成FCC(Face-centeredcubic)結構，Cu和Ni的晶體結構均為FCC，原子尺寸相差較小，能夠形成無限固溶。所以Co、Cu、Fe和Ni 4種元素能夠制備出單一相結構的高熵合金，有研究表明該類高熵合金表現出優異的塑性[2]。目前，對于各主元含量對CoCuFeNi高熵合金的晶體結構以及性能影響研究較少。因此，本文建立了CoCuFeNi系高熵合金第一性原理計算模型，并應用第一性原理密度泛函數理論和平面波贗勢方法對不同Cu、Co元素含量對CoCuFeNi系高熵合金晶體結構以及力學性能進行計算，進一步了解Cu、Co元素含量對該類高熵合金晶體結構和力學性能的影響。

1 理論基礎與計算方法

密度泛函理論(density functional theory,DFT)由Kohn和Honhenberg在1964年提出并證明[7]。DFT是應用電子密度的廣義函數對物質的性質、分子以及原子進行描述，電子密度僅是3個變量的函數，在計算多電子體系時，可大幅降低計算量。第一性原理計算中，用由電子和原子核組成的多粒子體系來近似多原子組成的體系，由原子核和電子的相互作用原理以及運動規律，再應用量子力學的原理，根據具體的要求，求解薛定諤方程。在利用第一性原理計算中，不需要參數，只需要基本的物理常量就可以得到體系基態的基本性質[8-11]。

本文第一性原理計算采用的是基于平面波贗勢方法的(cambridge sequential tatal energy package，CASTEP)軟件包，計算模型通過虛擬晶格近似(virtual crystal approximation,VCA)的方法建立，模型如圖1所示。Cu和Cr元素的摩爾分數、質量分數及其它元素含量，分別如表1和2所示。為了防止在建模過程中存在虛擬原子、長程結構等的累計誤差，建模時在單個FCC晶胞中建立晶體結構，并在每個原子上采用虛擬晶格近似[11]。在計算過程中，電子的交換關聯能采用廣義梯度近似(gengeral gradient approximation,GAA)下的質子平衡方程(perdew burke ernzerhof,PBE)，采用第一性原理的超軟贗勢(ultrasoft pseudopotential,USPP)處理電子-離子之間的交互作用[12-14]，計算平面波函數的動能截斷為640 eV，布里淵區K點取樣間距為0.004/nm，自洽計算(self-consistent field,SCF)采用Pulay密度混合法[15-16]，自洽計算的誤差為1.0×10-6eV/atom，自洽場迭代收斂條件為：兩個計算周期的總能量低于5.0×10-6eV/atom，公差偏移低于5.0×10-5nm。利用上述參數設置計算CoCuFeNi高熵合金的晶格常數為0.357 nm，與實驗值0.360 nm[2]相比，誤差為0.79%。因此，上述參數設置合理。

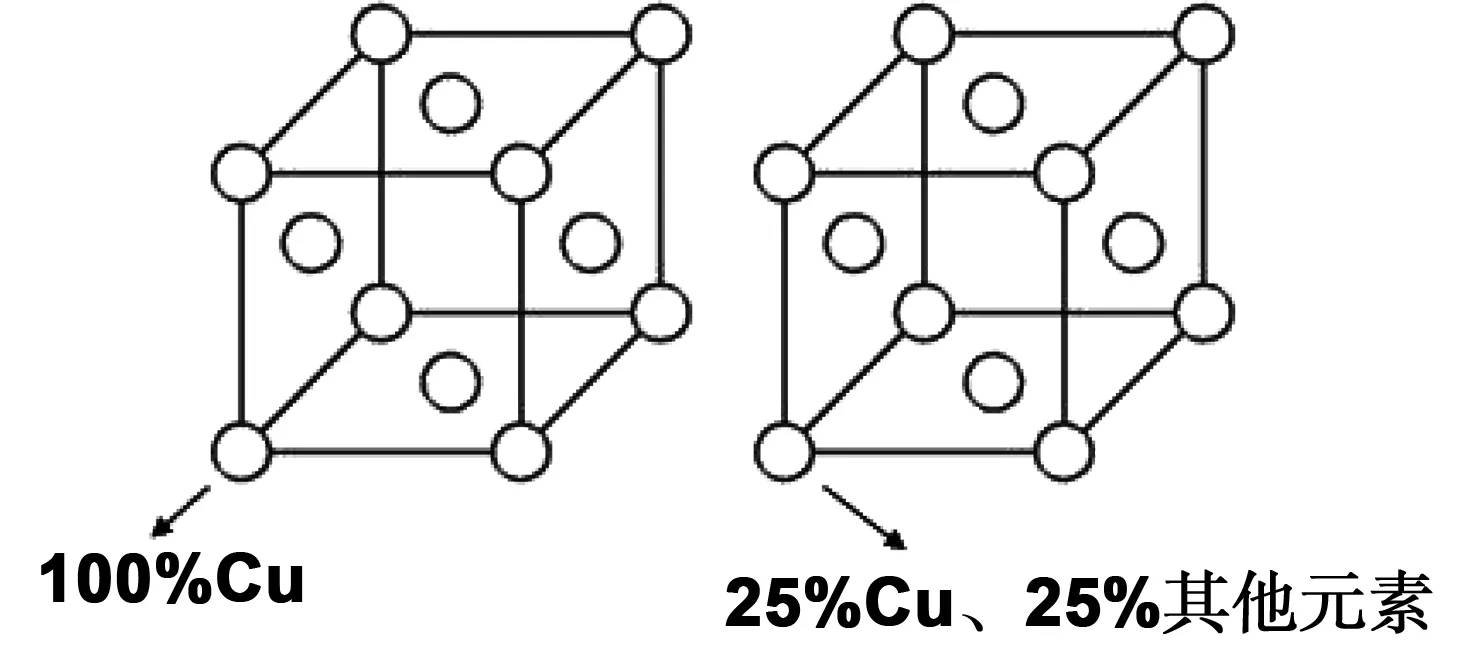
圖1 VCA建模示意圖Fig 1 VCA modeling diagram

表1 Cu元素的摩爾分數、質量分數及其它元素含量Table 1 Mole content and mass fraction of Cu and mass fraction of other elements

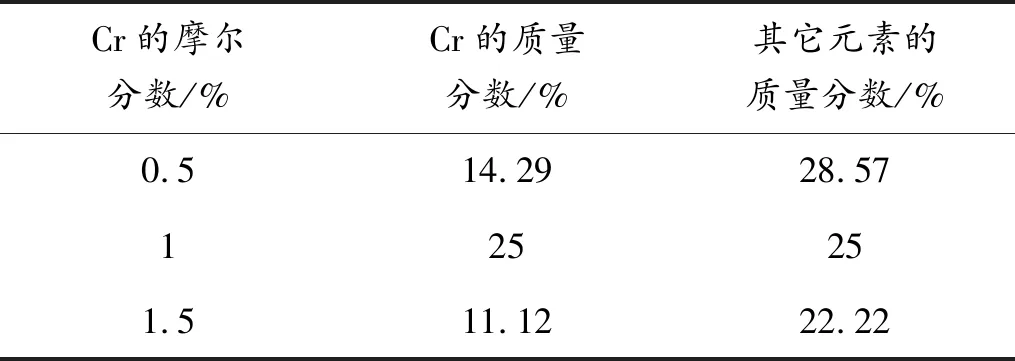
表2 Cr元素的摩爾分數、質量分數及其它元素含量Table 2 Mole content and mass fraction of Cr and mass fraction of other elements

2 計算結果與分析

2.1 Cu含量對CoCuFeNi系高熵合金的影響

利用上述參數設置，對CoCuxFeNi(x=0.5,1.0,1.5)高熵合金進行結構優化，優化后晶格常數、密度、基態總能量以及結合能，如圖2和3所示。從圖2可以看出，隨Cu含量的增加，CoCuxFeNi(x=0.5,1.0,1.5)高熵合金的晶格常數不斷增大，而密度不斷減小。這是由于Cu相比于其它組元具有較大原子半徑，所以隨著Cu含量的增加，高熵合金的晶格畸變效應更加顯著，晶格常數隨Cu含量的增加而增大。晶格畸變程度的增大，晶格常數的增大，晶胞體積增加，所以合金的密度隨Cu元素含量的增加而下降。體系結合能、基態總能量與體系的熱力學穩定性相關，結合能、基態總能量的絕對值越大體系在熱力學條件下越穩定[17]。從圖3可以看出，該類高熵合金體系的基態總能量與結合能都隨Cu含量的增加而降低，且均小于零。所以隨Cu含量的增加該高熵合金體系在熱力學條件下越穩定。由圖2和3可知，CoCu1.5FeNi高熵合金質輕且在熱力學條件下更穩定，其密度為8.508 g/cm3，基態總能量為-5 130.208 eV，結合能為-65.430 eV/atom。

通過對結構優化后的CoCuxFeNi(x=0.5,1.0,1.5)模型進行計算，獲得CoCuxFeNi(x=0.5,1.0,1.5)的彈性常數，如表3所示。該類高熵合金的晶體結構屬于立方晶系，根據彈性理論，其具有C11、C12和C443個獨立的彈性常數，彈性常數的計算見表3。根據立方晶系的力學穩定性判據[11]

C11>0;C44>0;C11-C12>0;C11+2C12>0

(1)

結合表3的計算結果，隨Cu的含量的變化，C11、C12、C44、C11-C12、C11+2C12的值均大于0，所以CoCuxFeNi(x=0.5,1.0,1.5)高熵合金符合力學穩定性條件。但是隨Cu的不斷添加，C11、C12、C44、C11-C12的值不斷減小，Cu的加入不利于CoCuxFeNi(x=0.5,1.0,1.5)高熵合金在力學上的穩定性。

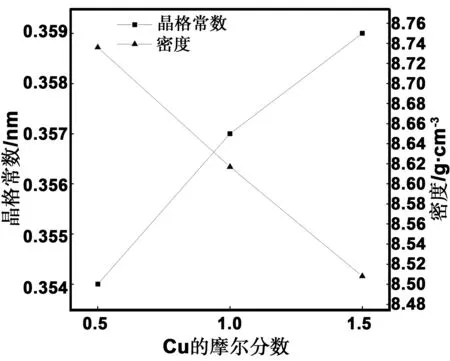
圖2 不同Cu含量的CoCuxFeNi(x=0.5,1.0,1.5)高熵合金晶格常數與密度的比較Fig 2 Comparison of lattice constants and densities of CoCuxFeNi(x=0.5,1.0,1.5) alloys with different Cu contents

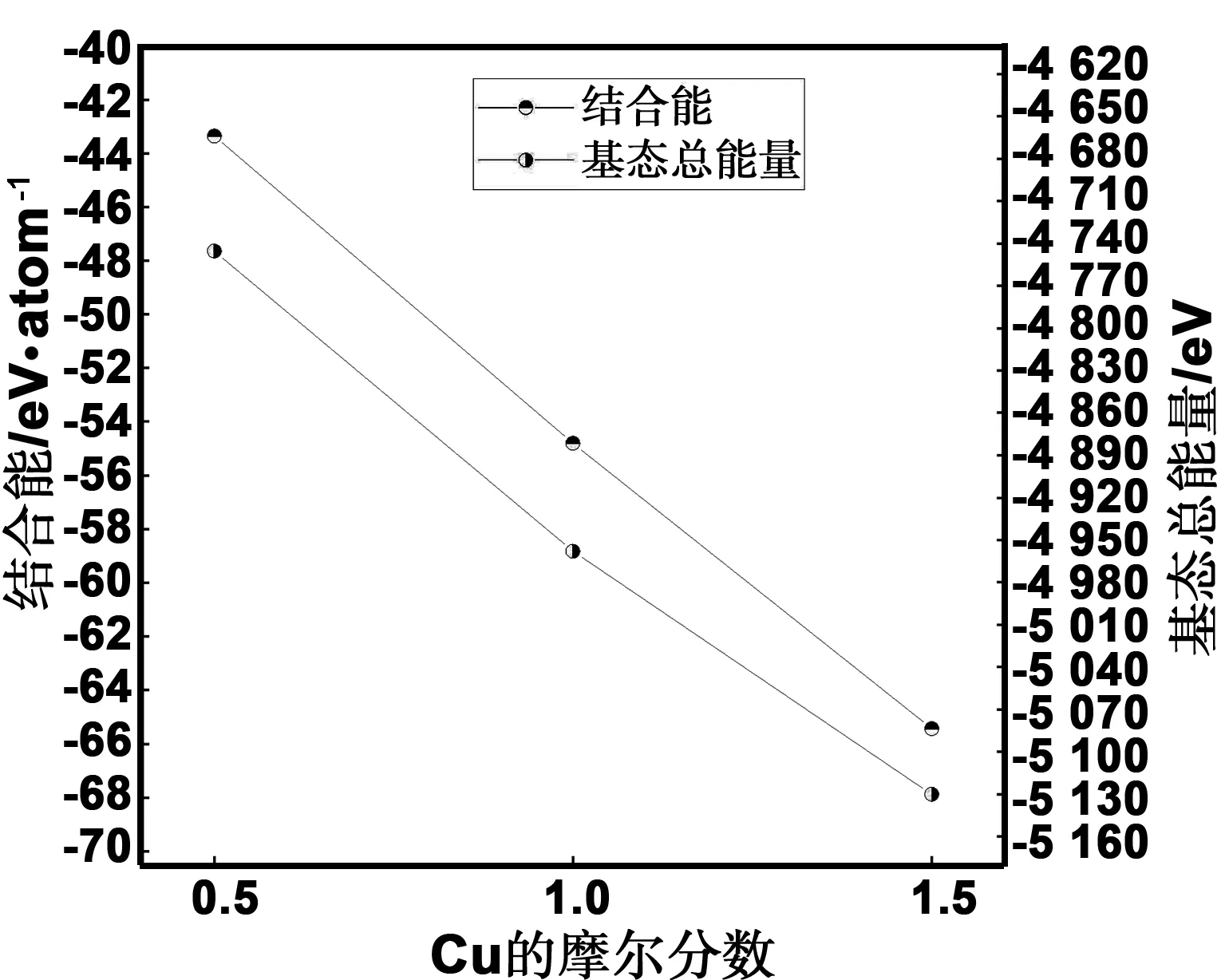
圖3 不同Cu含量的CoCuxFeNi(x=0.5,1.0,1.5)高熵合金的結合能與基態總能量的比較Fig 3 Comparison of totalenergy and binding energy of CoCuxFeNi (x=0.5,1.0,1.5) alloys with different Cu contents

表3 高熵合金CoCuxFeNi(x=0.5,1.0,1.5)彈性常數Table 3 Elastic constante of CoCuxFeNi (x=0.5,1.0,1.5) HEAs

根據彈性理論，對于立方晶系，其彈性常數滿足式(2)和(3)的關系[7]

B=(C11+C12)/3

(2)

c＇=(C11-C12)/2

(3)

其中，B為體積模量；c＇為剪切模量。結合第一性原理計算結果及式(2)和(3)，CoCuxFeNi(x=0.5,1.0,1.5)高熵合金單晶的體積模量K、彈性模量E以及剪切模量c＇，如表4所示。體積模量K、彈性模量E以及剪切模量c＇，分別表示材料抵抗體積變形、彈性變形以及剪切變形的能力。隨Cu含量的增加，體積模量K、彈性模量E不斷減小。剪切模量c＇隨Cu含量的增加呈現出先減小后增大的變化趨勢，CoCuFeNi高熵合金的剪切模量c＇最小；CoCu1.5FeNi高熵合金的剪切模量最大，表明隨Cu含量的增加，CoCuxFeNi(x=0.5,1.0,1.5)高熵合金抵抗體積變形、彈性變形的能力減弱，而抵抗剪切變形的能力先增大后減小。

采用Voigt-Reuss-Hill(VRH)的方法[9]進一步研究CoCuxFeNi(x=0.5,1.0,1.5)高熵合金多晶體力學性能。根據VRH方法獲得多晶體體積模量K、剪切模量G，如表5和6所示。由表5可知，通過VRH所獲得的多晶的體積模量與單晶的體積模量相同，而對于多晶的剪切模量，可采用式(4)計算[7]

G=(GV+GR)/2

(4)

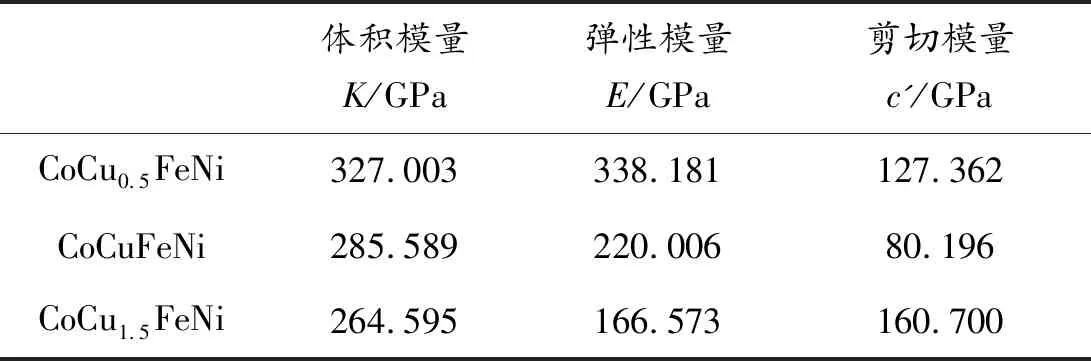
表4 高熵合金CoCuxFeNi(x=0.5,1.0,1.5)體積模量K、彈性模量E、剪切模量c＇Table 4 Bulk modulus K,elastic modulus E and shear modulus c＇of CoCuxFeNi (x=0.5,1.0,1.5) HEAs

對于多晶體彈性模量E以及泊松比υ,可由式(5)和(6)計算[7]

E=9BG/(3B+G)

(5)

υ=(3B-2G)/2(3B+G)

(6)

由式(5)和(6)計算多晶體彈性模量E、泊松比υ，如表7所示。分析表5-7發現，隨著Cu含量的增加，多晶體剪切模量G和彈性模量E不斷降低，多晶體泊松比υ隨Cu的含量增加而增加。對比CoCuFeNi系高熵合金多晶與單晶的力學性能可以看出，雖然體積模量K未發生變化，對于剪切模量G，隨Cu含量增加的變化趨勢產生了變化；對于彈性模量E，多晶體比單晶體高出了約120 GPa。產生上述變化是因為彈性模量具有各向異性，對于不同的晶向，彈性常數會發生變化，所以單晶與多晶的彈性模量不同。

材料的硬度、塑性與材料的剪切模量G、彈性模量E以及泊松比υ有關，當剪切模量G、彈性模量E越大，而泊松比υ越小時，材料的硬度越大，塑性越差[15]。對比表5和6的計算結果，隨Cu含量的增加，CoCuXFeNi(X=0.5,1.0,1.5)高熵合金的硬度不斷降低，塑性不斷增加，CoCu0.5FeNi高熵合金的硬度較高，CoCu1.5FeNi高熵合金的塑性較好。通過剪切模量G與體積模量B之比可以對金屬與金屬間化合物的塑性進行預測，當G/B<0.57時，材料表現出一定的延展性，為韌性材料，反之，為脆性材料[18]。不同Cu含量的CoCuFeNi系高熵合金G/B的值見表7。從表7可以看出，隨Cu的含量的變化，CoCuxFeNi(x=0.5,1.0,1.5)高熵合金的G/B值均小于0.57，所以CoCuxFeNi(x=0.5,1.0,1.5)高熵合金為韌性材料。通過上述分析可以發現，CoCuxFeNi(x=0.5,1.0,1.5)高熵合金是一種很好的韌性材料，隨Cu含量的降低，合金的硬度提高，所以CoCu0.5FeNi高熵合金具有很好的塑性，且硬度較高。

表5 采用VRH方法獲得的高熵合金CoCuxFeNi(x=0.5,1.0,1.5)多晶體積模量KTable 5 Polycrystallinebulk modulus K of CoCuxFeNi (x=0.5,1.0,1.5) HEAsobtainedby VRH

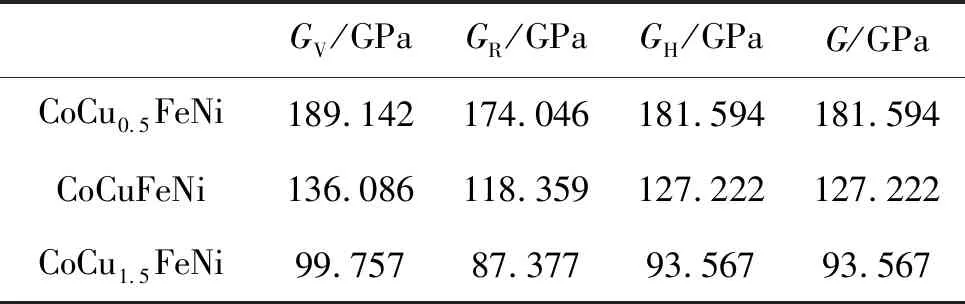
表6 采用VRH方法獲得的高熵合金CoCuxFeNi(x=0.5,1.0,1.5)多晶剪切模量GTable 6 Polycrystalline shear modulus G of CoCuxFeNi (x=0.5,1.0,1.5) HEAsobtainedby VRH

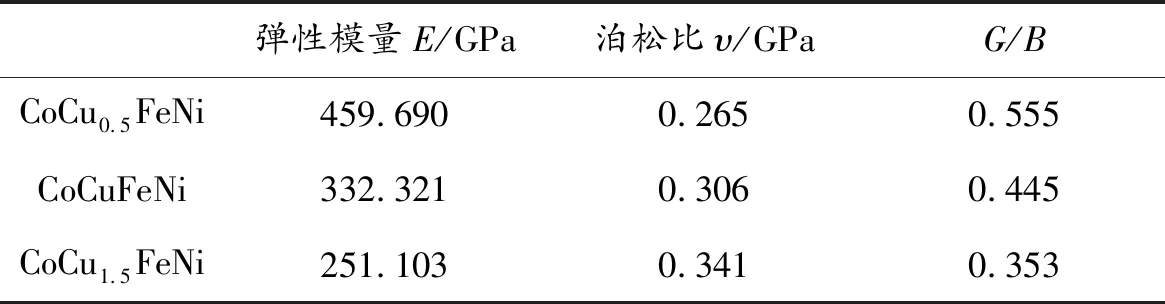
表7 高熵合金CoCuxFeNi(x=0.5,1.0,1.5)多晶彈性模量E、泊松比υ以及G/B值Table 7 Polycrystalline elastic modulusE,polycrystalline Poisson ratio υ and number of G/B of CoCuxFeNi (x=0.5,1.0,1.5) HEAs

2.2 Co含量對CoCuFeNi系高熵合金的影響

結構優化后的高熵合金CoxCuFeNi(x=0.5,1.0,1.5)晶格常數、密度、基態總能量和結合能如圖4和5所示。從圖4可以看出，隨Co的含量的增加，晶格常數不斷減小，而密度增加。這是由于隨Co含量的增加，原子半徑相對較大的Cu在體系中的含量減少，晶格畸變效應減弱，所以CoxCuFeNi(x=0.5,1.0,1.5)高熵合金的晶格常數隨Co含量增加而減小。由于晶格畸變效應減弱，晶格常數減小，晶胞體積縮小，所以該類高熵合金的密度隨Co含量的增加而增大。從圖5可以看出，隨Co含量的增加基態總能量與結合能不斷增大，所以CoxCuFeNi(x=0.5,1.0,1.5)高熵合金隨Co含量的增加熱力學穩定性減弱。對比圖4和5可知,Co0.5CuFeNi高熵合金質輕且在熱力學條件下更穩定，其密度為8.441 g/cm3，基態總能量為-5 076.609 eV，結合能為-64.205 eV/atom。

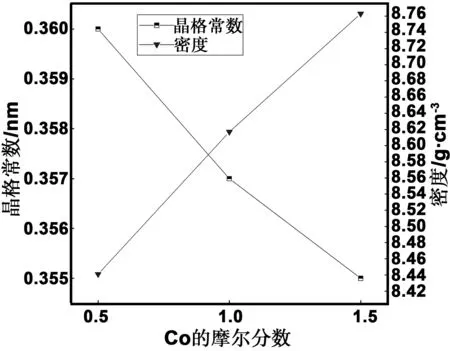
圖4 不同Co含量的CoxCuFeNi(x=0.5,1.0,1.5)高熵合金晶格常數與密度的比較Fig 4 Comparison of lattice constants and densities of CoxCuFeNi (x=0.5,1.0,1.5) alloys with different Co contents

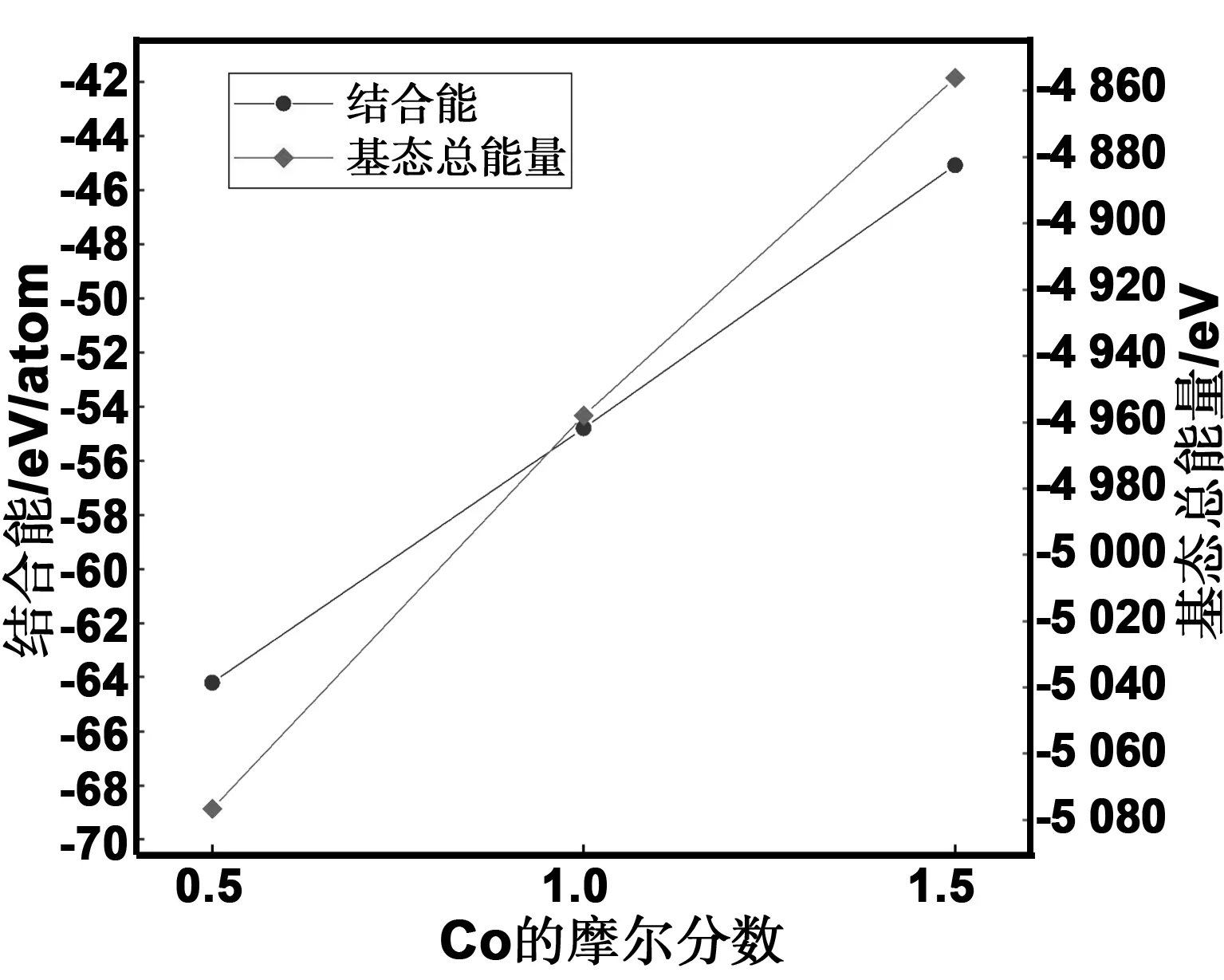
圖5 不同Co含量的CoxCuFeNi(x=0.5,1.0,1.5)高熵合金的結合能與基態總能量的比較Fig 5 Comparison of totalenergy and binding energy of CoxCuFeNi (x=0.5,1.0,1.5) alloys with different Co contents

計算所獲得的高熵合金CoxCuFeNi(x=0.5,1.0,1.5)的彈性常數,如表8所示，結合式(1)，隨Co含量的變化，C11、C12、C44、C11-C12以及C11+2C12的值恒大于0，所以CoxCuFeNi(x=0.5,1.0,1.5)高熵合金符合力學穩定性條件，隨著Co的不斷添加有利于CoxCuFeNi(x=0.5,1.0,1.5)高熵合金在力學上的穩定性。

表8 高熵合金CoXCuFeNi(X=0.5,1.0,1.5)彈性常數Table 8 Elastic constant of CoXCuFeNi (X=0.5,1.0,1.5) HEAs

結合表8與式(2)和(3)，得到CoXCuFeNi(X=0.5,1.0,1.5)高熵合金單晶的體積模量K、彈性模量E以及剪切模量c＇，如表9所示。由表9可知，體積模量K、彈性模量E和剪切模量c＇隨著Co的添加不斷增大。表明CoXCuFeNi(X=0.5,1.0,1.5)高熵合金抵抗體積變形、彈性變形以及剪切變形的能力，隨Co含量的增加而增大。

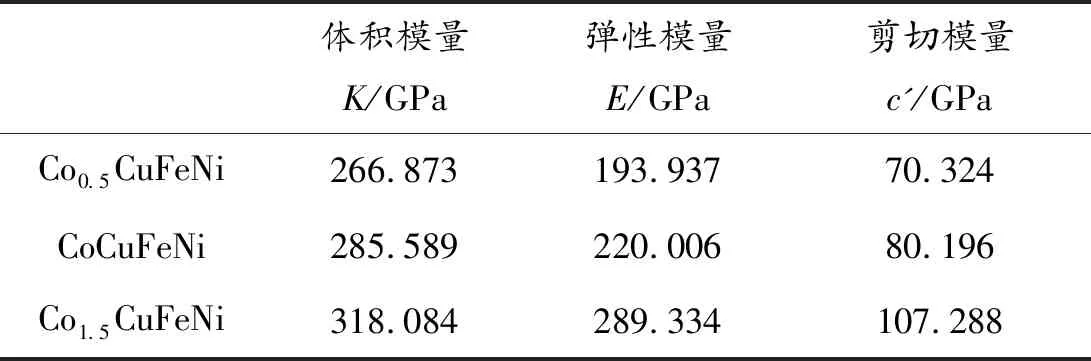
表9 高熵合金CoXCuFeNi(X=0.5,1.0,1.5)體積模量K、彈性模量E、剪切模量c＇Table 9 Bulk modulus K,elastic modulus E and shear modulus c＇ of CoXCuFeNi (X=0.5,1.0,1.5) HEAs

采用VRH方法結合式(4)～(6)，獲得高熵合金CoXCuFeNi(X=0.5,1.0,1.5)多晶體積模量K、剪切模量G、彈性模量E以及泊松比υ，如表10—12所示。多晶體剪切模量G、彈性模量E都隨Co增加而增大，多晶體泊松比υ隨Co含量增加而減小，所以隨Co含量的增加合金的硬度提高，Co1.5CuFeNi高熵合金具有較高的硬度。高熵合金CoXCuFeNi(X=0.5,1.0,1.5)的G/B值均小于0.57，所以高熵合金CoCoXCuFeNi(X=0.5,1.0,1.5)具有良好的塑性。

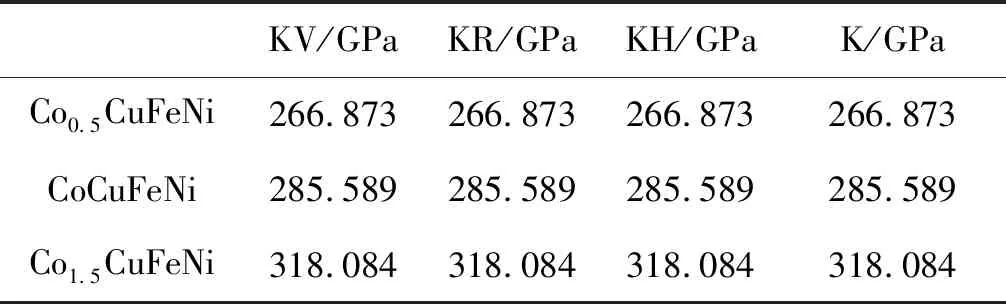
表10 采用VRH方法獲得的高熵合金CoxCuFeNi(x=0.5,1.0,1.5)多晶體積模量KTable 10 Polycrystalline bulk modulus K of CoxCuFeNi(x=0.5,1.0,1.5) HEAs obtainedby VRH

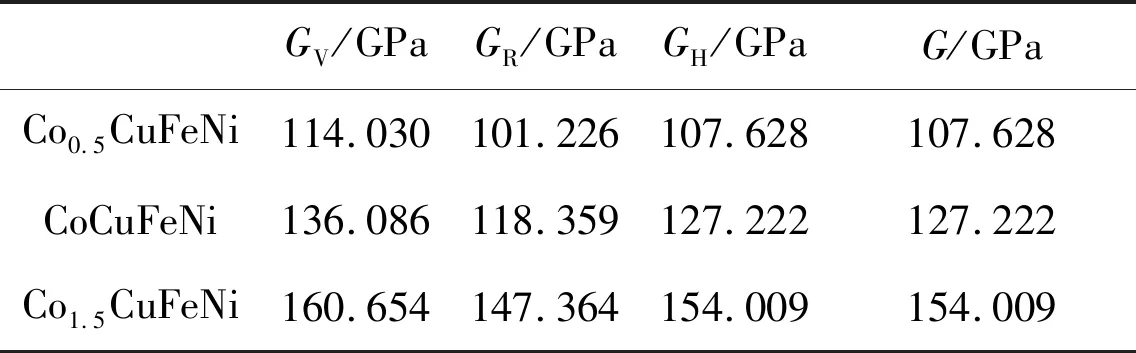
表11 采用VRH方法獲得的高熵合金CoxCuFeNi(x=0.5,1.0,1.5)多晶剪切模量GTable 11 Polycrystalline shear modulus G of CoxCuFeNi (x=0.5,1.0,1.5) HEAs obtainedby VRH

表12 高熵合金CoxCuFeNi(x=0.5,1.0,1.5)多晶彈性模量E、泊松比υ以及G/B值Table 12 Polycrystalline elastic modulus E,polycrystalline Poisson ratio υ and number of G/B of CoxCuFeNi (x=0.5,1.0,1.5) HEAs

表13為CoCu0.5FeNi和Co1.5CuFeNi高熵合金的晶體結構、力學性能。由表13可知，CoCu0.5FeNi和Co1.5CuFeNi高熵合金具有相近的晶格常數、密度以及結合能，CoCuFeNi系高熵合金中增加Co的含量與降低Cu含量所產生的影響相同，由于高熵合金在性能方面所具有的“雞尾酒”效應，高熵合金的性能與各組元有關，所以高熵合金組元含量的降低與其相對含量的降低對合金所產生的影響是相同的。從表13可以看出，CoCu0.5FeNi高熵合金的彈性模量E、剪切模量G均高于Co1.5CuFeNi高熵合金，泊松比υ小于Co1.5-CuFeNi高熵合金，所以CoCu0.5FeNi高熵合金具有更高的硬度。CoCu0.5FeNi、Co1.5CuFeNi高熵合金G/B的值均小于0.57，所以兩類高熵合金表現出優異的塑性。對于CoCuFeNi系高熵合金，降低合金中Cu的含量，可實現具有優異塑性的同時，大幅提升合金的硬度。

表13 CoCu0.5FeNi和Co1.5CuFeNi高熵合金的晶體結構、力學性能Table 13 Crystal structure and mechanical properties of CoCu0.5FeNi and Co1.5CuFeNi HEAs

3 結 論

(1)隨Cu含量的增加，CoCuxFeNi(x=0.5,1.0,1.5)高熵合金的晶格常數增大，密度不斷減小，結合能不斷降低，體系熱力學穩定性提高。CoCu1.5FeNi高熵合金質輕且結構更加穩定。CoCuxFeNi(x=0.5,1.0,1.5)高熵合金具有良好的塑性，其中CoCu0.5FeNi高熵合金的硬度較高，體積模量K、剪切模量G以及彈性模量E的值分別為327.003，181.594 和459.690 GPa，均高于其它Cu含量的CoCuxFeNi高熵合金。

(2)隨Co含量的增加，CoxCuFeNi(x=0.5,1.0,1.5)高熵合金的晶格常數減小，密度不斷增大，結合能不斷升高，體系熱力學穩定性降低。Co0.5CuFeNi高熵合金質輕且更加穩定，其密度為8.441 g/cm3，基態總能量為-5 076.609 eV，結合能為-64.205 eV/atom。CoxCuFeNi(x=0.5,1.0,1.5)高熵合金仍具有良好的塑性，Co1.5CuFeNi的硬度較高，體積模量K、剪切模量G以及彈性模量E的值分別為為318.084，154.009和397.823 GPa，均高于其它Co含量的CoxCuFeNi高熵合金。

(3)高熵合金組元含量的降低與其相對含量的降低對合金所產生的影響是相同的。對于CoCuFeNi系高熵合金，降低合金中Cu的含量，可實現具有優異塑性的同時，大幅提升合金的硬度。