水電站壩后淺埋壓力管道結構優化數值模擬研究

徐高瑞

(新疆維吾爾自治區昌吉回族自治州昌吉市努爾加水庫建設管理處，新疆 昌吉 831100)

1 工程背景

某水電站工程為一等大(Ⅰ)型工程，永久性主要建筑物級別為1級，設計洪水標準為200年一遇，校核洪水標準為2 000年一遇，該電站的正常蓄水位為725.00 m，設計洪水位為726.10 m，校核洪水位為726.54 m。電站工程主要由混凝土重力壩、發電廠房以及輸水系統組成。電站的輸水系統按照水流流向可以分為引水系統和尾水系統，其中引水系統由進水口、引水隧洞以及壓力鋼管組成。根據相關設計資料，壓力鋼管采取單管單機引水體系，單根鋼管的內徑為4.0 m，鋼襯厚度為40 mm，外包混凝土的厚度為1.0 m。管內最大設計流速為2.56 m/s，設計引流量為32.20 m3/s，鋼管在運行期的最大內水壓力為2.28 MPa。

2 壓力管道有限元分析

2.1 有限元模型的構建

水電站壩后淺埋壓力管道的內徑為4.0 m，外包厚度為1.0 m的C25鋼筋混凝土。其中，鋼筋的配置為4層，里圈為2層，參數為?32@20和?25@20；外圈為2層，為?32@20，間距為20 cm。結合工程實際，選用ANSYS有限元軟件的DM模塊進行壓力管道的三維有限元實體模型構建[1]。對構建的幾何模型，采用多區域法進行六面體8節點網格剖分，獲得的三維有限元模型[2]見圖1。全局單元尺寸為50 mm，最終獲得11 296個計算單元，28 987個計算節點。

圖1 壓力管三維有限元模型

結合壓力管道的實際運行條件和受力特征，在管道下半圓的外壁面施加固定約束[3]。根據電站的具體情況和工程現狀，設計了建成工況、運行工況以及校核工況。不同工況的荷載情況見表1。

表1 計算工況設計

2.2 有限元模擬計算結果分析

2.2.1 建成工況

利用上節構建的三維有限元軟件，對壓力管道進行建成工況下的應力和位移分布情況進行模擬計算，獲得管道應力和位移分布云圖，見圖2。由圖2可知，在建成工況下，壓力管道的最大位移值1.051 mm，產生在壓力管道的頂部；壓力管道鋼襯的最大應力值為32.17 MPa，位于管道的半腰部位。由于管道鋼襯材料的屈服強度為330 MPa，遠大于其受到的最大應力值。因此，壓力管道受到的應力和應變不大，存在比較大的優化設計空間[4]。

2.2.2 運行工況

利用上節構建的三維有限元軟件，對壓力管道進行運行工況下的應力和位移分布情況進行模擬計算，獲得管道應力和位移分布云圖，見圖3。由圖3可知，在運行工況下，壓力管道的最大位移值5.48 mm，產生在壓力管道的頂部；壓力管道鋼襯的最大應力值為158.00 MPa，位于管道的半腰部位。由于管道鋼襯材料的屈服強度為330 MPa，遠大于其受到的最大應力值。因此，壓力管道受到的應力和應變不大，存在比較大的優化設計空間。

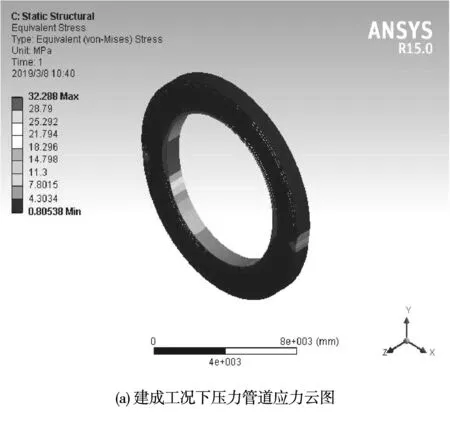
圖2 建成后管道應力和位移分布云圖

圖3 運行期間管道應力和位移分布云圖

2.2.3 校核工況

利用上節構建的三維有限元軟件，對壓力管道進行校核工況下的應力和位移分布情況進行模擬計算，獲得管道應力和位移分布云圖見圖4。由圖4可知，在校核工況下，壓力管道的最大位移值6.26 mm，產生在壓力管道的頂部；壓力管道鋼襯的最大應力值為192.62 MPa，位于管道的半腰部位。由于管道鋼襯材料的屈服強度為330 MPa，遠大于其受到的最大應力值。因此，壓力管道受到的應力和應變不大，存在比較大的優化設計空間。綜合上述，在3種不同工況下，電站壩后淺埋壓力管道的應力和應變量都不大，存在比較大的優化設計空間。

圖4 校核工況下管道應力和位移分布云圖

3 壓力管道結構優化設計

根據上文的有限元模擬計算結果可知，電站壩后淺埋壓力管道的應力和應變量都不大，存在比較大的優化設計空間。說明原始設計中壓力管道的管身結構尺寸較大，混凝土的應力設計存在較大的余量，整體結構設計偏于保守。因此，本文在管徑不變的情況下，對管身結構尺寸進行重新規劃，采用鋼筋和混凝土分離模型驗證優化結果的合理性。

3.1 數學模型的建立

在進行基于ANSYS Workbench的具體優化操作之前，首先要建立以數學表達式為主要形式的數學模型。這些表達式由描述優化方面的變量表達式、控制優化過程的限制表達式以及決定具體優化方向的目標表達式構成[5]。在設定好上述表達式之后，即可將其以參數的形式輸入計算機，進而模擬優化結果[6]。

針對本次研究的實際情況，優化計算過程中的變量為鋼管的厚度以及環筋的折算厚度。其表達式為：

X=[t,d]r

(1)

式中：t為鋼管厚度，mm；d為環筋折算厚度，mm，d=(A×N)/l；A為環筋的等效面積，mm2；N為環筋數量；l為長度，mm。

在本次研究中，狀態表達式為：

σθ≤σ0

(2)

P

(3)

t>δmin

(4)

式中：σθ為每層鋼筋的環向應力，MPa；σ0為每層鋼筋的允許應力，MPa；P為設計外壓力值，kN；Pcr(d)為設計外臨界壓力值，kN；t為鋼襯厚度，mm；δmin為鋼襯最小厚度，mm。

由于目標表達式函數值的大小是由變量表達式的函數值決定的，因此目標表達式中必須要包含變量表達式[7-8]。在本次優化中，目標表達式為：

V=(t+d)×1,V→min

(5)

3.2 優化計算結果與分析

利用上節構建的數學模型，在Workbench Design Exploration中對壓力管道結構進行優化分析，獲得2.28 MPa的最大內部水壓下的優化成果。見表2。

表2 參數優化候選點

3.3 優化前后對比分析

按照最優設計順序，選擇鋼襯厚度最小的方案，也就是第一種方案，在運行工況下加載與原設計相同的負荷進行結構優化效果對比分析，優化后的管道應力分布云圖和應變分布云圖見圖5。與原方案的對比結果見表3。

圖5 優化后管道應力應變分布云圖

表3優化方案和原方案對比

計算方案原設計方案優化方案最大應力值/MPa158.00151.3最大位移量/mm5.485.20體積/m31.07231.0103

兩種方案的計算結果顯示，優化后的壓力管道實際變形量、最大應力值和體積較原方案均有所減小。其中，實際變形量減小0.28 mm，最大應力值減小6.7 MPa，體積減少0.062 m3。由此可見，優化后的方案不僅在壓力鋼管的結構性能上得到一定的改善，同時也減少了鋼材的消耗量，有利于節省工程投資。

3.4 討 論

在研究中將壓力管道內的內水壓強分為0.3，0.6，0.9，1.2和1.5 MPa等5個不同等級，采用逐級加壓的方式重復進行上述優化計算過程，得到在不同管道內水壓強條件下的計算成果，其變化特征見圖6。

圖6 不同內水壓強下的壓力管道結構變化規律

由圖6可知，管道的內水壓力對管道鋼襯厚度的影響較大，對鋼筋折算厚度的影響相對較小。因此，在壓力管道的優化設計中，應該對鋼襯的結構特征設計予以足夠的重視。

4 結 論

本文以某水電站壩后淺埋壓力管道為例，利用有限元數值模擬分析方法對壓力管道結構優化進行研究，并獲得如下主要結論：

1) 在建成工況、運行工況以及校核工況下，壓力管道的應力和應變量都不大，整體結構設計偏于保守，存在比較大的優化設計空間。

2) 在管徑不變的情況下，對管身結構尺寸進行優化。優化后的壓力管道實際變形量、最大應力值和體積較原方案均有所減小，同時還減少了鋼材的消耗量，有利于節省工程投資。

3) 管道的內水壓力對管道鋼襯厚度的影響較大，在壓力管道的優化設計中應該予以足夠的重視。