次成分提取信息準則的加權規則方向收斂分析

杜柏陽，孔祥玉，馮曉偉

（1.火箭軍工程大學導彈工程學院，陜西 西安 710025；2.火箭軍工程大學核工程學院，陜西 西安 710025）

1 引言

在信息處理領域，次成分（MC,minor component）是指輸入信號的自相關矩陣中與最小特征值對應的特征向量，次子空間（MS,minor subspace）是指由多個次成分張成的子空間。提取次成分和跟蹤次子空間的算法分別被稱為次成分分析（MCA,MC analysis）算法和次子空間跟蹤（MSA,MS analysis）算法。MCA 算法和MSA 算法在總體最小二乘[1]、自適應波達方向估計[2]、曲面擬合[3]、穩健波束分析[4]等問題中具有重要應用。

傳統的代數次成分批處理法只能處理離線的、靜態的信號，且具有較高的計算復雜度。實際中的信號往往是在線獲取的動態數據，因而傳統方法的應用十分受限。相比而言，神經網絡算法能夠處理的信號不受上述2 個條件的限制[5]，并且許多神經網絡算法具有較小的計算復雜度。近年來，學者們提出了許多MSA 和MCA 的神經網絡算法[5-7]。在這些算法中，M?ller[5]算法只能提取單個次成分，PAST（projection approximation subspace tracking）算法[8]、Ojam 算法[9]和Kong 等[2]所提的算法可以跟蹤輸入信號的次子空間，Jankovic 等[10]所提的算法和AMMD（adaptive multiple minor direction）算法[11]可以提取輸入信號的多個次成分。上述研究都是單獨針對MSA 或者MCA 問題開展的，實際上，MSA 和MCA 算法之間存在一定關聯，在一定條件下可以相互轉換。例如，Jankovic 等[10]通過TOHM（time-oriented hierarchical method）轉化裝置實現了MSA 算法到MCA 并行算法的轉換，Thameri 等[12]則通過Givens 旋轉實現了MSA 算法到MCA 算法的轉變。這種通過轉化轉置實現算法轉化的方法具有結構復雜、計算復雜度較高的缺點[13]。另一種行之有效的轉化方法是使用加權規則。然而，目前關于加權規則的研究還比較少。文獻[14]介紹了用于提取多個次成分的加權信息準則。目前，對經過加權的次成分分析算法的性能分析與傳統的單維次成分提取算法的性能分析大體相同，主要集中于算法的收斂性、自穩定性等。而實際上，經過加權的算法能夠實現多個次成分同時提取，該性能是傳統單維次成分提取算法所不具備的，需要研究多個次成分在提取過程中的方向收斂問題。目前，研究并行多個提取問題的學者主要將興趣集中于算法的提出，極少有對方向收斂問題開展探討。那么，加權規則對于MSA 信息準則轉變為MCA 信息準則的過程發揮了什么樣的作用，這樣的作用過程對于其他子空間提取信息準則的轉變是否具有普適性？這個問題的解答對靈活轉換各種先進的成分提取算法，增加人們對提取算法本質和多種性質的理解具有十分重要的意義。

多個次成分可以張成一個次子空間，因而通常認為多個次成分的提取算法是次子空間跟蹤算法的進步。Toshihisa[15]通過研究多個次成分提取算法的廣義加權規則，指出廣義加權規則的參數對提取算法的收斂速度存在影響，即加權規則的參數變化會引起算法的性質變化。當參數的取值沿著實數軸負方向變化時，加權矩陣則逐漸近似為單位矩陣，算法的提取能力逐漸由多個次成分提取退化為次子空間跟蹤。

實際上，只有一部分次子空間提取算法在使用加權規則后可以轉化為多個次成分的提取算法。次子空間與次成分的偏離程度可以通過次子空間的組成向量與次成分之間的夾角表示。當提取算法逐漸穩定以后，次子空間跟蹤算法狀態矩陣的夾角是一個隨機值，而轉化為多個次成分提取算法狀態矩陣的夾角總是某個對角矩陣。這說明加權規則的加入改變了該夾角的變化規則。本質上，信息準則函數在算法對信息的歸類方式、算法提取信息的方式等方面存在隱性的規定，因而信息準則對夾角的變化方式具有決定作用。因此，通過理論分析信息準則對MSA 和MCA 算法狀態矩陣夾角的作用過程，能夠反映算法的一些本質特性。

本文主要針對加權規則對次成分提取算法的信息準則的作用進行分析，以PAST 的次子空間跟蹤算法為例，通過構建提取算法的動力學表達，對比有加權規則和無加權規則下的次子空間跟蹤信息準則，挖掘信息準則對狀態矩陣與次成分的方向夾角的梯度差異。本文專門對一類次成分分析算法的方向收斂性能進行總結，并同時采用理論和仿真的方法對該性能開展分析。

2 加權規則

Yang[8]在研究子空間跟蹤問題時提出次子空間PAST 算法，該算法的信息準則為

其中，W ∈Rn×r為算法的狀態矩陣，n 為輸入信號的維數，r 為需要提取的次成分個數，R=E[xxT]∈Rn×n為輸入信號x 的自相關矩陣，E[·]表示數學期望。假設R 是滿秩矩陣且特征值互不相同，那么，輸入信號有n 個特征向量 φi，i=0,1,…,n-1。當存在一個向量 W=Wn，使信息準則函數值 J1(W)取得最小值時，Wn就等價于信號的次子空間，也就是前r 個特征向量 φi張成的子空間。

PAST 信息準則對應的加權信息準則（WPAST,weighted PAST）為

其中，D=diag(d1,d2,…,dr)∈Rr×r為一個對角矩陣，其作用是為狀態矩陣加權，其各元素降序排列。類似于PAST 算法的信息準則，當 W=Wn時，J2(W)取得最小值，此時Wn的各列向量恰好等于R 的前r 個特征向量 φi。顯然，當加權矩陣等于單位陣時，WPAST 信息準則退化為PAST 信息準則。

以上2 個信息準則求取相應跟蹤提取算法是通過梯度下降法實現的，其基本的計算式為

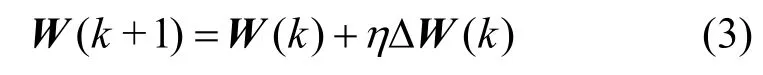
其中，ΔW(k)為算法的搜索方向，文獻[15]指出，該方向為信息準則的梯度下降方向，即ΔW(k)=；W(k)為第k 步迭代中的狀態矩陣，其維度與式(1)中W 相同；η ∈(0,1)為次成分提取算法的學習因子。另外，有些算法采用可變步長來加速算法的收斂過程，但是只要步長設置合理就只影響算法的收斂速度而不影響其收斂行為。因此，為了簡化算法分析過程，假設學習因子是固定長度的。

式(1)信息準則對W 的梯度為

根據牛頓梯度下降法，可得

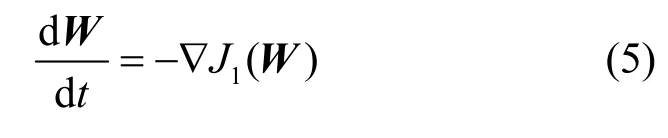
進而，可以得到PAST 算法的常微分方程形式為

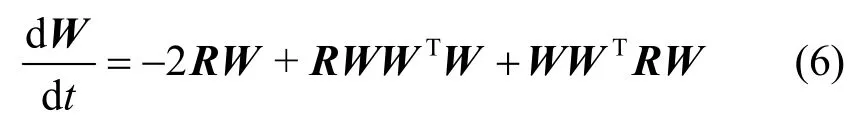
文獻[8]的收斂性分析表明，該算法能夠有效地在線跟蹤信號的次子空間。定義狀態向量和實際次成分方向的偏轉矩陣為M1∈Rn×r，實際次成分組成的矩陣為P=[φ0,φ1,…,φn-1]。由于矩陣M1一定位于由P 張成的空間中，于是狀態矩陣W 可以改寫為W=PM1，其中M1隨著W 變化。當算法收斂后，M1的前r 行元素收斂為某個旋轉矩陣，后n-r行元素收斂為0。

同理，式(2)信息準則經過梯度下降法推導，可得WPAST 算法的常微分方程形式，如式(7)所示。

該算法能夠有效地在線并行提取多個次成分。類似地，存在一個M2∈Rn×r，使W=PM2。總體而言，2 種算法的穩定點PM1和PM2都包含信號的次成分，說明這2 種算法都提取出信號中能量較小的部分信息。不同之處在于，M1的前r 行和前r 列是一個旋轉矩陣，這代表PAST 算法跟蹤的次子空間與信號的真實次成分方向存在偏角，而且這個偏角隨跟蹤過程的變化而變化。在WPAST算法提取多個次成分時，M2的前r 行和前r 列元素最終收斂到一個對角矩陣。這說明與PAST算法相比，WPAST 算法因為加權而附加了角度變化的屬性，這個屬性決定了WPAST 算法具備多個次成分提取的能力，而PAST 算法則只能提取次子空間。本文通過分析M1和M2變化的差別，從微觀角度探究加權規則對算法的動力學特性的影響。

3 次成分提取過程動力學分析

不同維數提取過程有不同的角度數量。一維特征提取時，次子空間退化為次特征向量，此時2 種算法效果一致。二維特征提取時，旋轉矩陣包含一個旋轉角度。三維特征提取時，旋轉矩陣包含2 個角度。依次類推，多維次成分分析算法提取r 維特征時，旋轉矩陣包含的角度數量為個。

需要說明的是，因一維特征提取算法不具有旋轉角度信息，此時只需要考慮模值收斂性，此種情況已被確定離散時間（DDT,determinate discrete time）方法[16]廣泛分析。因此，本文僅針對二維及以上的信號特征進行分析。下面從二維特征情況入手分析，并以二維特征為基礎，逐步分析高維特征提取過程。

定理1考慮二維旋轉矩陣M1只有一個旋轉角度，那么對信息準則 J1(W)而言，其對該旋轉角度的二階導數為0。

證明已知二維旋轉矩陣只有一個旋轉角，假設M1的旋轉角度為θ，則M1可以表示為

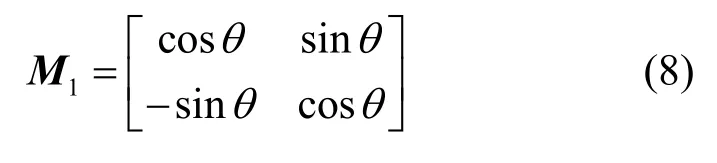
此時，信息準則式(1)則表示為

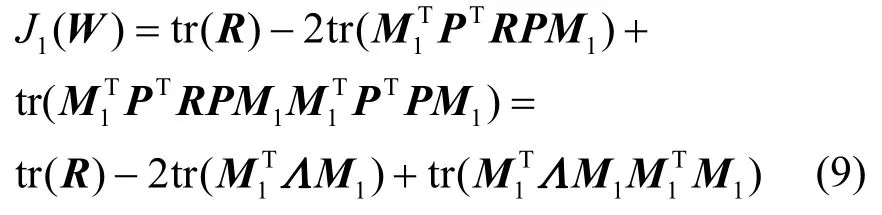
信息準則對角度的梯度可以通過梯度下降法求得，如式(10)所示。

其中，有

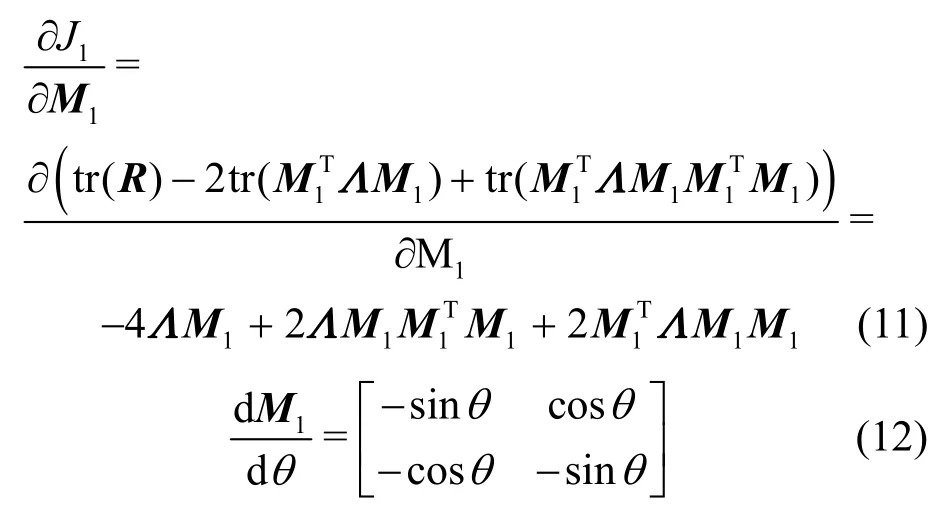
因而可以得出

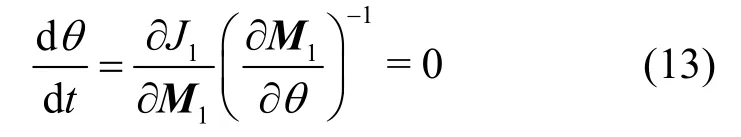
式(13)表明不存在某一點，使在該點處狀態向量與信號次成分方向的夾角最小。也就是說，信息準則 J1(W)不能確定狀態矩陣的各個向量與信號次成分方向的變化。

證畢。

信息準則對角度的二階導數為0，說明信息準則沒有規定旋轉角度的變化方式。具體地，在信息準則的任何一點上，狀態矩陣中各個向量與對應次成分的夾角的導數以及其本身是不確定的。另外，從導數的角度理解定理1，則有在信息準則式(1)的梯度算法下，提取出的次子空間與信號次成分的夾角和算法設置的狀態矩陣初值相關。實際上，加權規則能夠改變信息準則的這個性質。具體過程可以通過定理2 說明。

定理2考慮二維旋轉矩陣M2只有一個旋轉角度，那么對信息準則 J2(W)而言，其對該旋轉角度的二階導數不為0。

證明令M2的旋轉角度為θ，那么M2可以表示為

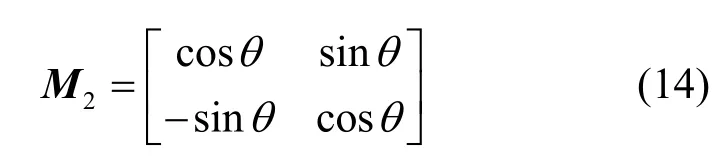
此時，信息準則式(2)則表示為

同樣地，該信息準則對角度的梯度也可通過梯度下降式求解，可得

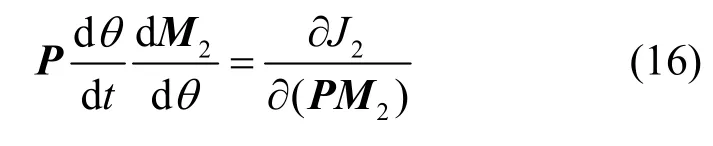
其中，有

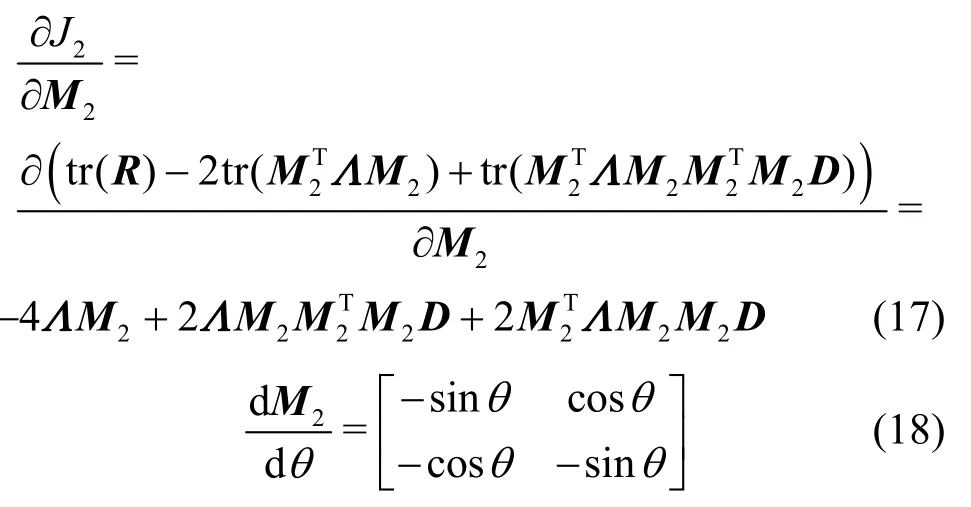
此時，可得

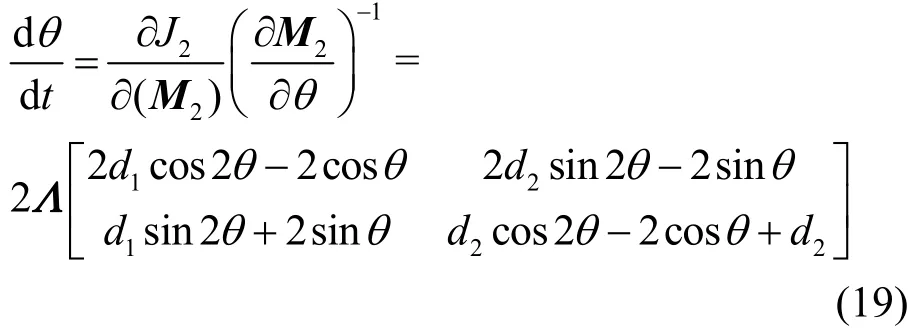
信息準則 J2(W)對角度二階導數不為0，說明信息準則規定了旋轉角度的變化方式。具體地，在信息準則的任何一點上，狀態矩陣中各個向量與對應次成分的夾角的導數是確定的，而且在極小值點處，狀態矩陣中各個向量與對應次成分的夾角的導數以及其本身都是確定的。

證畢。

以上分析是在n=2、r=2這一特殊情況下進行的。為使結論更具有一般性，下面進一步討論n＞2、r=2的情況。

推論1當n＞2、r=2時，二維旋轉矩陣Mi，i=1,2各只有一個旋轉角度，信息準則 J1(W)對旋轉角度的二階導數為0，而信息準則 J2(W)對旋轉角度的二階導數不為0。

證明文獻[8]已經證明，對于n＞2、r=2的情況下的 J1(W)和 J2(W)，對應的梯度算法都能夠跟蹤次子空間。即W 的后n-r列元素總是逐漸變化為0。不妨認為，當迭代次數大于某一個大數時，狀態矩陣可以表達為，i=1,2。問題轉化為n=2、r=2的情況，此時結合定理1 和定理2 的結論可知，信息準則 J1(W)對旋轉角度的二階導數為0，而信息準則 J2(W)對旋轉角度的二階導數不為0。

分析推論1 的結論可知，只要提取二維特征向量，信息準則 J1(W)對角度二階導數為0，即在J1(W)的任何一點上，狀態矩陣中各個向量與對應次成分的夾角的導數以及其本身是不確定的。信息準則 J2(W)對角度二階導數不為0，即在 J2(W)的任何一點上，狀態矩陣中各個向量與對應次成分的夾角的導數是確定的，并且在極小值點處，狀態矩陣中各個向量與對應次成分的夾角的導數以及其本身都是確定的。

在n=r、r＞2的情況下，主要考慮歐拉轉角描述所有的角度變化。假設第j 個相角變化為 θj，j=1,2,…,r，根據歐拉轉角規則，第j 個角是在第j-1個角的基礎上進一步旋轉的。例如r=3時旋轉矩陣M*表示為

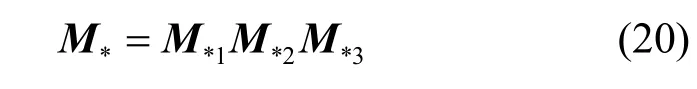
其中，M*1和M*2分別為

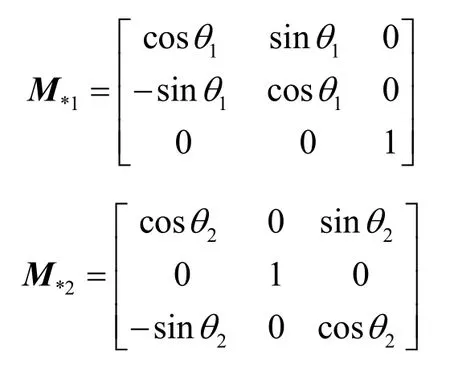
依次類推，將1 放在不動軸的位置，并且該元素所在行和列的其他元素均為0，不動軸的數量為r-2，則旋轉次數為

推論2當n=2、r ＞2 時，信息準則 J1(W)對旋轉角度的二階導數為0，而對信息準則 J2(W)對旋轉角度的二階導數不為0。

證明類似于定理1 和定理2 的證明步驟，信息準則式(1)表示為

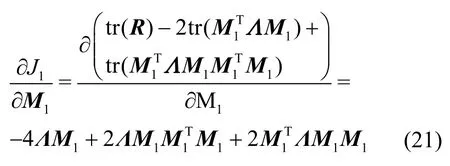
不同的是此時的旋轉矩陣變為

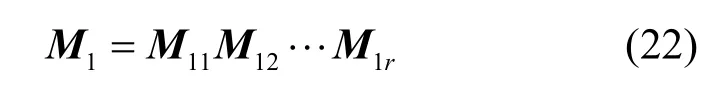
同時，信息準則對角度的梯度表達為多個計算式，如下所示。

由式(25)可得

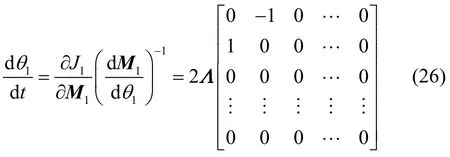
顯然，對于未加權的信息準則 J1(W)，對于任意θ 恒成立。類似地，對加權信息準則，有

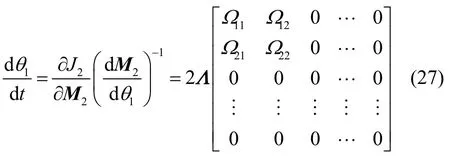
其中，有

對于n ＞r、r＞2的情況，其基本思路同推論1，即通過分析一定條件下狀態矩陣各個向量的長度變化情況，最終轉化為n=r、r＞2的情況，并結合推論2 的結論實現對該情況的討論。

證畢。

通過上述定理和推論可知，加權規則對提取算法產生影響的本質因素是加權矩陣改變信息準則在方向上的梯度變化。這對研究的啟發是在考慮將次子空間提取算法改進成并行提取算法時，其核心步驟是使算法在狀態矩陣與實際次成分的夾角方向上產生梯度。

4 數值分析與仿真校驗

為直觀展示加權算法的方向收斂屬性，本文通過2 組數值算例對比 J1(W)和 J2(W)這2 種信息準則的方向收斂性能。實驗中，輸入信號的真實次成分P=[φ0,φ1,…,φn-1]是通過離線的特征值分解方法計算得到的。

4.1 2 個次成分提取算例

該算例展示2 種信息準則對狀態矩陣各個向量與信號次成分方向提取的不同表現。加權矩陣規定為D=diag(1,2)。令θ 表示狀態矩陣的單個向量與對應次成分方向的夾角，設置θ 的變化區間為(0,2π]，實驗中均勻提取了10 000 個點，點間最小間距為。通過θ 可以表示旋轉矩陣，通過M*可以表示狀態向量W=PM*，狀態向量在第一次成分方向的投影為X，在第二次成分方向的投影為Y，又根據式(1)和式(2)可以分別表示 J1和 J2，仿真結果分別如圖1～圖4 所示。

圖1 PAST 信息準則和WPAST 信息準則在θ 變化情況下的數值變化

圖2 PAST 信息準則和WPAST 信息準則在處的投影

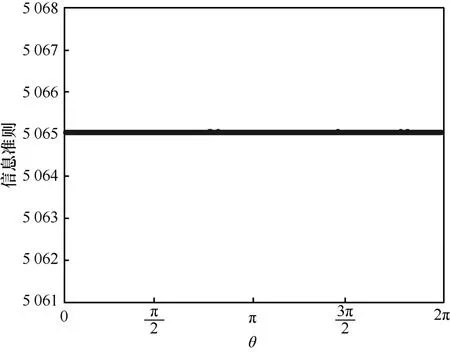
圖3 PAST 信息準則在θ 變化情況下的數值變化

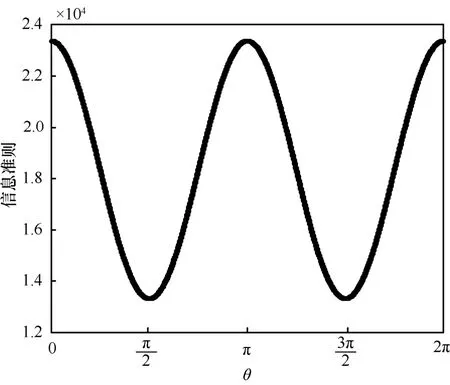
圖4 WPAST 信息準則在θ 變化情況下的數值變化

圖1 中，外側的曲面圓錐為PAST 信息準則函數值變化情況，內側的曲面圓錐為WPAST 信息準則函數值變化情況。首先，函數值會隨著狀態矩陣中向量模值的變化而變化，為清晰地表征這個特點，該算例在某一個固定的角度投影2 個信息準則函數，如圖2 所示，這說明信息準則函數能夠提取信號的次成分信息。其次，2 個曲面變化都具有對稱性。其中，內側的曲面圓錐是隨著θ 周期對稱的，這印證了定理2 的結論，而外側的曲面圓錐是處處對稱的。

另外，2 個曲面的變化也存在差別。首先，觀察向量模長固定，θ 在區間(0,2π]變化時，2 個函數的變化情況。由圖1 中外側的曲面圓錐可知，在θ 變化的情況下，PAST 信息準則函數值沒有變化。為了直觀展示，在圖1 中做狀態矩陣模長為1.5、θ在區間(0,2π]上的圓柱面，將圓柱面與函數曲面圓錐的交線向底面投影并展開，展開的結果如圖3 所示。由圖1 中內側的曲面圓錐可知，WPAST 信息準則函數值在θ 變化的情況下，呈現三角函數的變化形態。為了直觀展示，采用與外側圓錐曲面相同的步驟得到投影的展開結果，并展示在圖4 中。其次，觀察θ 值一定時2 個函數沿著模值長度的變化情況。如圖2 所示，WPAST 函數的斜率絕對值明顯大于PAST 函數的斜率絕對值。

上述實驗分析表明，在提取2 個次成分方向的情況下，PAST 信息準則不能確定狀態矩陣各向量與對應次成分的方向關系，而WPAST 信息準則能夠確定狀態矩陣各向量與對應次成分的方向關系。這驗證了定理1 和定理2 對PAST 和WPAST 信息準則的理論分析結果。

4.2 多個次成分提取算例

多個次成分的信息準則對應的坐標系超過三維，不容易直觀表示，因此該算例主要通過PAST和WPAST 信息準則的提取算法在實際提取過程中的角度變化來展示加權規則對信息準則的角度關系的確定作用。假設提取狀態矩陣的維數為4，加權矩陣為D=diag(1,2,3,4)，狀態矩陣各個向量與對應次成分的夾角分別為 θ1、θ2、θ3、θ4，狀態矩陣的各向量與對應次成分的方向余弦為

其中，ui表示輸入信號的次成分，可通過特征值分解方法提前計算出來，wi(k),i∈{1,2,3,4}表示算法在提取過程中的狀態矩陣的單個向量，k 表示提取過程中的迭代次數，T 表示轉置運算，表示求范數運算。

夾角的計算式為

需要說明的是，此處將方向余弦和方向夾角都作為實驗結果展示。PAST 算法的結果分別如圖5和圖6 所示，WPAST 算法的結果分別如圖7 和圖8 所示。

圖5 PAST 算法的狀態矩陣各向量與對應次成分夾角θ 變化情況

圖6 PAST 算法的狀態矩陣各向量與對應次成分方向余弦變化情況

圖7 WPAST 算法的狀態矩陣各向量與對應次成分夾角θ 變化情況

如圖5 所示，橫坐標為迭代次數，按照10 的指數變化，縱坐標為方向夾角數值，其弧度值在區間內變化。PAST 算法的4 個方向夾角在經過振蕩過程后，均呈現穩定狀態。但是，穩定的常數各不相同。該特點在圖6 中也有體現，方向余弦經過一段振蕩過程，都穩定在一定的數值上。相比PAST 算法，WPAST 算法的方向夾角收斂過程比較長，且最終都穩定在0 附近。如圖7 所示，4 個方向夾角最后都以不同的形式收斂到0 附近，這說明WPAST 算法狀態矩陣的4 個向量最后都收斂到對應次成分的方向。圖8展示的方向余弦也印證了WPAST算法的方向收斂性。在35 ×10次迭代后，狀態矩陣各向量的方向余弦都接近1。需要說明的是，由于三角函數的非線性，在圖7 中接近510 處的方向夾角振蕩較劇烈，且都在區間內，圖8 中對應的方向余弦都在區間(0.95,1.00)內振蕩，振蕩范圍非常小。

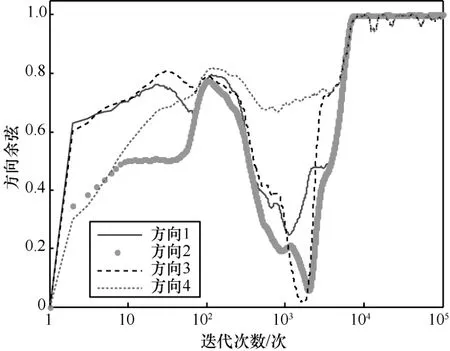
圖8 WPAST 算法的狀態矩陣各向量與對應次成分方向余弦變化情況

5 結束語

本文通過分析PAST 信息準則和WPAST 信息準則的差異，從二維到多維逐步推導出加權規則能夠改變狀態矩陣和信號次成分的旋轉矩陣梯度的結論。一方面，從理論上解釋了加權規則對信息準則的作用規律，提高人們在信息準則層次認識影響算法性能的因素；另一方面，對于不能通過加權規則轉化為多個次成分提取算法的次子空間跟蹤算法，研究成果為推進未來并行提取多個次成分分析算法發展提供了研究思路和改進方向。