基于Zadoff-Chu 矩陣的最優(yōu)碼本構造方法

李玉博，劉勝毅，張景景，賈冬艷

（1.燕山大學信息科學與工程學院，河北 秦皇島 066004；2.河北省信息傳輸與信號處理重點實驗室，河北 秦皇島 066004；3.河北科技師范學院數(shù)學與信息科技學院，河北 秦皇島 066004）

1 引言

碼本是一類具有較低相關性的信號集，在同步碼分多址（CDMA,code division multiple access）通信系統(tǒng)[1]、量子編碼理論[2]以及壓縮感知領域具有重要應用[3]。構造參數(shù)達到理論界限的最優(yōu)碼本是現(xiàn)代通信理論的重要研究課題之一，因此碼本構造方法的研究受到人們的廣泛關注。一般來說，碼本C 由2 個參數(shù)進行表示，即(N,K)，其中，N 表示碼本的數(shù)量，K 表示碼本的長度。碼本的字符集是碼本中所有碼字的坐標所采用的不同復數(shù)值的集合，字符集大小是字符集中元素的數(shù)量。在實際應用中，字符集較小的碼本具有重要的意義。另外，碼本的最大互相關幅度值用 Ima（Cx）表示。在通信系統(tǒng)中，希望碼本的最大互相關幅度值 Ima（Cx）越小越好，以盡可能消除信號之間的干擾。在壓縮感知領域，具有低相關性的碼本可用于構造測量矩陣。根據(jù)壓縮感知理論可知，碼本最大互相關幅度值Ima（Cx）越低，其對應的測量矩陣RIP（restricted isometry property）性能越好[2]。除此之外，在量子信息領域中[3]，碼本還用于構造SIC-POVM（symmetric informationally complete positive operator-valued measure）和無偏正交基（MUB,mutually unbiased base）。碼本的參數(shù)受到理論界限的制約，當N ≥K時，稱最大互相關幅度值滿足Welch 界限的碼本為最優(yōu)碼本；當N ＞K2時，稱最大互相關幅度值滿足Levenstein 界限的碼本為最優(yōu)碼本。近年來，研究人員提出了很多近似達到Welch 界或Levenstein 界的碼本構造方法。文獻[4]首次利用差集構造了最優(yōu)碼本。Ding 等[5-6]進一步利用差集和幾乎差集構造了參數(shù)達到Welch 界的最優(yōu)碼本。文獻[7-10]利用分圓類方法構造了具有優(yōu)良參數(shù)的碼本。除此之外，還有一些利用bent 函數(shù)[11]、平坦函數(shù)[12]、有限域上的特征和理論[13-16]以及二元線性碼[17]來構造碼本的方法。

近年來，文獻[18]提出一類基于二元序列與變換矩陣的碼本構造框架。該框架包含了已有的許多碼本構造方法，如文獻[4-6]的方法等。該類方法有2 個關鍵因素：1)滿足一定條件的變換矩陣的構造；2)二元序列支撐集的選取。現(xiàn)有的碼本構造方法大部分都是基于已有的變換矩陣如離散傅里葉逆變換（IDFT,inverse discrete Fourier transform）矩陣、Hadamard 矩陣，通過選取不同的二元序列支撐集來構造碼本。基于同樣的思想，文獻[19-20]通過選取一類新的二元序列構造了一類新的最優(yōu)碼本。本文放寬了文獻[18]對初始變換矩陣的條件限制，構造了一類新的變換矩陣，并結合現(xiàn)有的一些特殊的整數(shù)集合構造了參數(shù)達到漸進最優(yōu)的碼本。

2 基本概念

一個參數(shù)為(N,K)的碼本是一個復向量集合C={ C0,C1,…,CN-1}，其中每個向量Cn=(cn,0,cn,1,…,cn,K-1)是長度為K 的單位復向量，其中0≤ n ≤N-1，。對于任意2 個向量Cn1,Cn2∈C，定義厄米特（Hermitian）內(nèi)積為，其中(·)H表示向量的共軛轉置。向量集合C 中最大互相關幅度值定義為

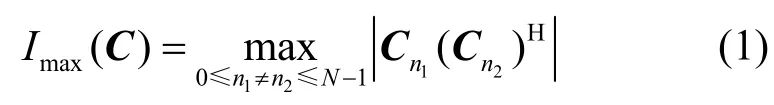
對于碼本的最大互相關幅度值，有以下界限成立。

引理1[4]對于一個參數(shù)為(N,K)的碼本C，其中N ≥ K，則有

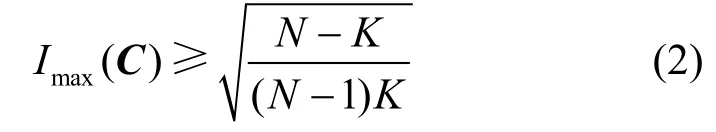
式(2)中等號成立的條件是當且僅當對于任意的0≤n1≠n2≤N-1，有

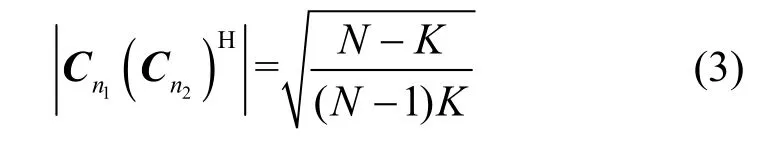
當式(3)成立時，則碼本最大互相關幅度值達到Welch 界限，稱為 MWBE（maximum-Welchbound-equality）碼本；當N ＞K2時，不存在達到Welch 界的(N,K)碼本，此時Levenstein 界更緊。

引理2[11]對于任意參數(shù)為(N,K)的實碼本，若，則有

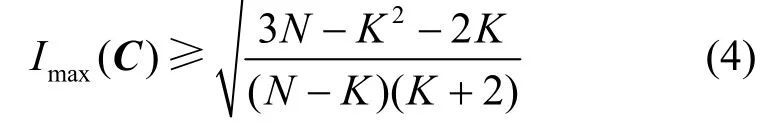
對于任意參數(shù)為(N,K)的復數(shù)碼本，若N ＞K2，則有

一般稱達到Welch 界或Levenstein 界的碼本為最優(yōu)碼本，對于最優(yōu)碼本的構造方法研究具有重要的應用價值。

設p 為素數(shù)，F(xiàn)p表示包含有p 個元素的有限域，。令ZN={0,1,2,…,N-1}表示一個模N 的整數(shù)環(huán)。

定義1設q=pn是素數(shù)冪，p 為素數(shù)，令α 表示循環(huán)群的生成元，有限域上的乘法特征定義為

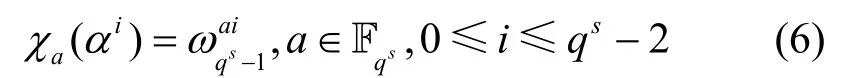
定義2設集合D={d0,d1,d2,…,dK-1}表示有限域Fp上一個子集，定義集合D 的差函數(shù)為，τ∈Fp。如果滿足當τ 取遍 Fp上非0 元素時，差函數(shù) fD(τ)取值為λ 出現(xiàn)p-1次，則稱集合D 是有限域 Fp上的一個差集，參數(shù)表示為(p,K,λ)-DS。

顯 然，對 于 差 集(p,K,λ)-DS，有K(K-1)=(p-1)λ成立。

定義3設集合D={d0,d1,d2,…,dK-1}表示有限域Fp上一個子集，定義集合D 的差函數(shù)為，τ ∈Fp。如果滿足當τ 取遍 Fp上非0 元素時，差函數(shù) fD(τ)取值為λ 出現(xiàn)t 次，取值為 λ +1出現(xiàn)p-1-t次，則稱集合D 是有限域 Fp上的一個幾乎差集，參數(shù)表示為(p,K,λ,t)-ADS。

定義4令D={d0,d1,d2,…,dK-1}表示整數(shù)環(huán)ZJ上一個含有K 個不同整數(shù)的集合，dk∈ZJ，0≤ k ≤K-1。集合D 的特征序列定義為一個二元序列a=(a0,a1,…,aJ-1)，其中有

則稱集合D 為序列a=(a0,a1,…,aJ-1)的支撐集。顯然，序列的漢明重量。

定義5設N,γ 是2 個互質(zhì)的正整數(shù)，則Zadoff-Chu 序列族的第γ 行序列可以表示為

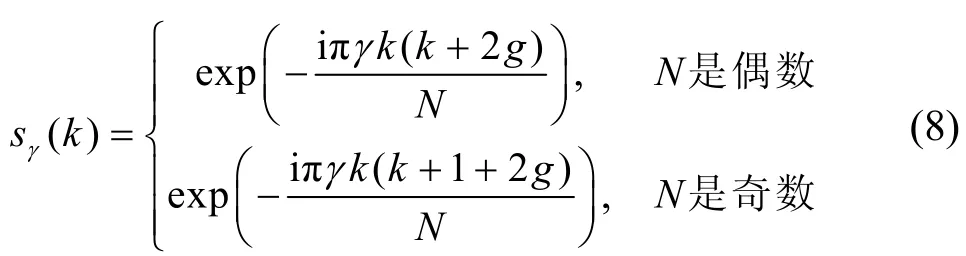
其中，k=0,1,…,N-1，g 是一個整數(shù)。

3 基于二元序列的碼本構造框架

文獻[18]提出一類基于二元序列的碼本構造框架，其構造過程如下。

步驟1定義一個變換矩陣，令φi,l表示矩陣中任意元素，0≤i ≤J-1，0≤l ≤N-1。矩陣滿足以下性質(zhì)。

性質(zhì)1每個矩陣元素具有單位幅值，即。

性質(zhì)2任意2 個不同列向量滿足=φi,l，0 ≤l1≠l2，l ≤N-1，0≤i ≤J-1。

性質(zhì)3矩陣Φ 的第一列為全1 向量，即φi,0=1，0≤i ≤J-1。

性質(zhì)4對于任意0＜l≤N-1，有。

滿足上述性質(zhì)的變換矩陣已知的有N × N的Hadamard 矩陣和IDFT 矩陣。

步驟2取二元序列 a=(a0,a1,…,aJ-1)，序列的漢明重量wt(a)=K，設集合D={d0,d1,d2,…,dK-1}是序列a 的支撐集。構造碼本CΦ(a)={C0,C1,…,CN-1}為

其中，Cl為構造的碼本中的一個行向量，集合D 是變換矩陣Φ 的行索引集，即元素φdk,l(0≤ k ≤K-1)是矩陣中第 dk行、第l 列元素，則 CΦ(a)即為得到的(N,K)碼本，其最大互相關幅度值 Imax(CΦ(a))可以由變換矩陣與二元序列的支撐集計算得到。

文獻[18]構造的框架包含了已有的一些碼本構造方法作為特殊情況。例如，當選取N × N階的IDFT 矩陣作為變換矩陣Φ 時，若選取的二元序列對應的支撐集為差集時，得到的碼本 CΦ(a)即為文獻[4]的結果。若二元或復Hadamard 矩陣作為矩陣Φ，則選取的二元序列對應支撐集為幾乎差集時，得到的碼本 CΦ(a)為文獻[5-6]的結果。該構造框架有2 個關鍵因素：1)變換矩陣Φ 的選取；2)二元序列a 的支撐集選取。基于該構造框架，文獻[19]通過選取不同的二元序列構造了參數(shù)幾乎最優(yōu)的碼本。同時文獻[19]也指出，可以通過構造新的變換矩陣來構造新的碼本，然而并沒有給出新的變換矩陣構造方法。文獻[20]同樣采用Hadamard 矩陣作為變換矩陣，通過設計一類新的二元序列進而構造了一類最優(yōu)碼本。本文從另一個角度出發(fā)，通過設計新的變換矩陣來構造新的碼本。

4 最優(yōu)碼本的構造

本文提出的新的構造方法介紹如下。

步驟1根據(jù)定義5，令g=0，γ =1，N 是偶數(shù)，得到Zadoff-Chu 矩陣的第一行。令，k=0,1,…,N-1，由此定義 Zadoff-Chu 矩陣為

其中，0≤ s,t ≤N-1。文獻[21]中令矩陣Φ 的N 為偶數(shù)來構造測量矩陣，而本文取N 為奇數(shù)的情況來構造碼本。

步驟2設D={d0,d1,d2,…,dK-1}表示整數(shù)環(huán)ZN上一個含有K 個不同整數(shù)的集合，dk∈ZN，0≤ k ≤K-1。構造碼本CΦ={C0,C1,…,CN-1}為

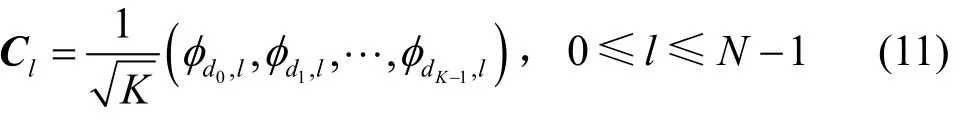
則 CΦ即為得到的(N,K)碼本。

定理1令CΦ為本文新的構造法得到(N,K)碼本，則最大相關幅度值為

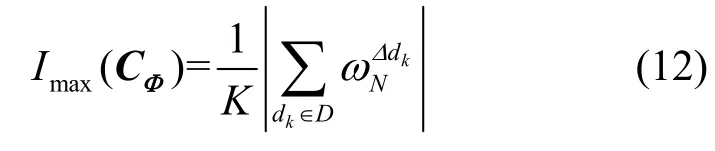
證明設 Cl,Ct∈ CΦ，0≤t≠l ≤N-1，則有

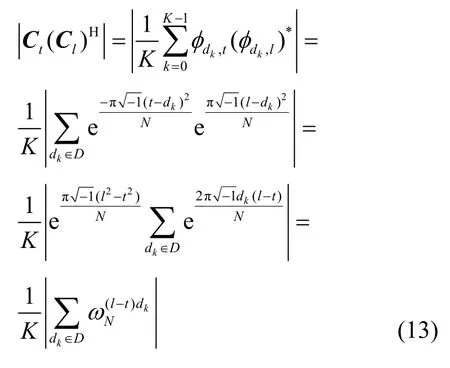
證畢。

4.1 基于差集的最優(yōu)碼本

引理3[5]令集合D={d0,d1,d2,…,dK-1}表示有限域 Fp上的一個差集(p,K,λ)-DS，則對于任意γ≠0(mod p)有

根據(jù)引理3，可以得到下面結論。

定理2令N=p為素數(shù)，若集合D={d0,d1,d2,…,dK-1}為有限域 Fp上的一個差集(p,K,λ)-DS，則式(9)定義的碼本參數(shù)為(p,K)，碼本的字符集大小為2p，最大相關幅度值為，該碼本達到Welch 界。

證明碼本的最大相關幅度值可以由定理1 和引理3 直接得到。根據(jù)引理1 可知，該碼本最大相關幅度值等于Welch 界，是一類最優(yōu)的碼本。

證畢。

例1令p=7，取集合 D={1,2,4}，可知其是一個差集(7,3,1)-DS，得到(7,3)碼本為

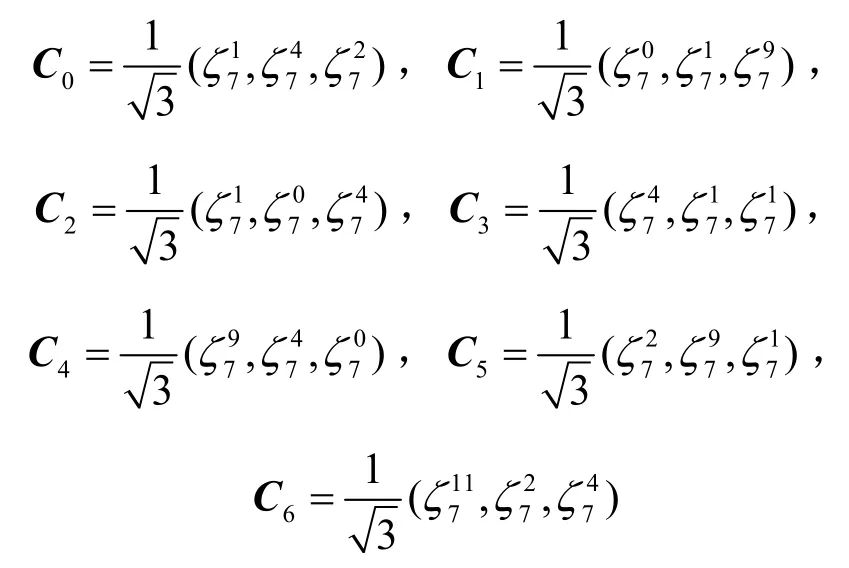
定理2 得到的碼本與文獻[4,18]具有相同的參數(shù)和相同的最大相關幅值，但不是同一類碼本。由于變換矩陣的選擇不同，2 類碼本內(nèi)部的元素也不相同。文獻[4,18]的碼本選取的變換矩陣是IDFT 矩陣，字符集更小；而定理2 構造的碼本的變換矩陣是Zadoff-Chu 矩陣，限制條件更少，構造更靈活。例如，選取同樣的差集 D={1,2,4}，文獻[4,18]得到的碼本為

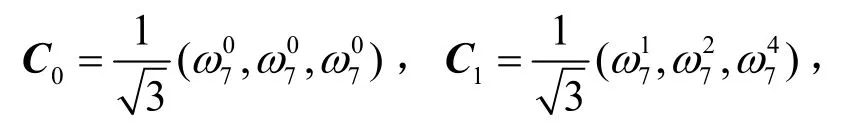
4.2 基于幾乎差集的最優(yōu)碼本

引理4[5]令p=1(mod4)，則2階分圓類是有限域Fp上的幾乎差集，參數(shù)為,-ADS。對于該幾乎差集，Δ≠0，有

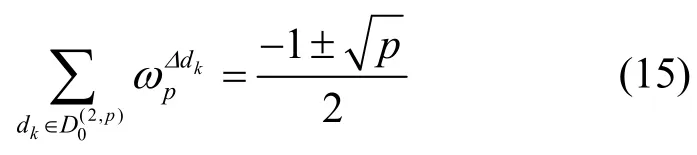
根據(jù)引理4，可以得到下面結論。

定理3令N=p為素數(shù)，若集合D={ d0,d1,d2,…,dK-1}為有限域Fp上的幾乎差集,-ADS，即，則式(9)定義的碼本參數(shù)為，碼本的字符集大小為2p，最大相關幅度值為。該碼本漸進達到Welch 界。

證明根據(jù)構造過程可知向量數(shù)目N=p，向量長度，計算其互相關幅度如下。由引理4可知，對于幾乎差集，有≤。又由定理1 可得，碼本最大相關幅度值為

可以看出，當p 增大時，該碼本漸進達到Welch 界。

證畢。

4.3 基于特征和的最優(yōu)碼本

令 ξK表示K 維希爾伯特空間的標準正交基所構成的集合，即由下面K 個長度為K 的向量ei(1≤i ≤K)組成的集合為

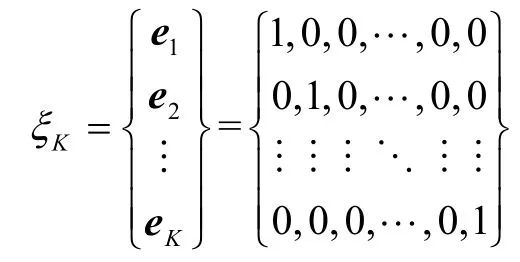
其中，e1=(1,0,···,0)，e2=(0,1,···,0)，·· ·，eK=(0,0,···,1)。

設q=pn是素數(shù)的冪，其中p 為素數(shù)。令a∈Fq，定義集合。有限域上的艾森斯坦和（Eisenstein sum）定義為

引理5[22]令χ 表示有限域上的非平凡乘法特征，對于任意，有

定理4令s=2，N=q2-1，a 是有限域的本原元，。選取集合D={d0,d1,d2,…,dK-1}為dk=logax，

設CΦ表示式(9)定義的碼本，則CΦ∪ξK是(q2+q-1,q)碼本，碼本的字符集大小為2p+1，其最大互相關幅度為。

證明由上述構造過程可知向量長度K==qs-1=q，向量數(shù)目為N=q2+q-1。其互相關幅度值計算如下。

當 Cl,Ct∈ξK時，很容易得。

當 Cl∈ξK，Ct∈CΦ時，有。

當 Cl,Ct∈ CΦ時，根據(jù)定理1 有

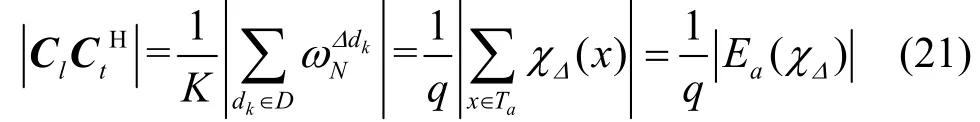
定理5碼本CΦ∪ξK依照Levenstein界是漸進最優(yōu)的。

證明對于參數(shù)為(q2+q-1,q)的復數(shù)碼本CΦ∪ξK，其中N ＞K2，根據(jù)引理2 可得，最大互相關幅度值的Levenstein 界為式(5)，即

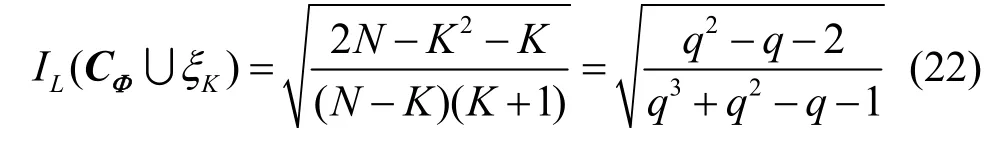
進一步可得

證畢。

5 最優(yōu)碼本構造方法的對比分析

對基于文獻[18]的框架思想提出的幾類最優(yōu)碼本構造方法進行比較，如表1 所示。

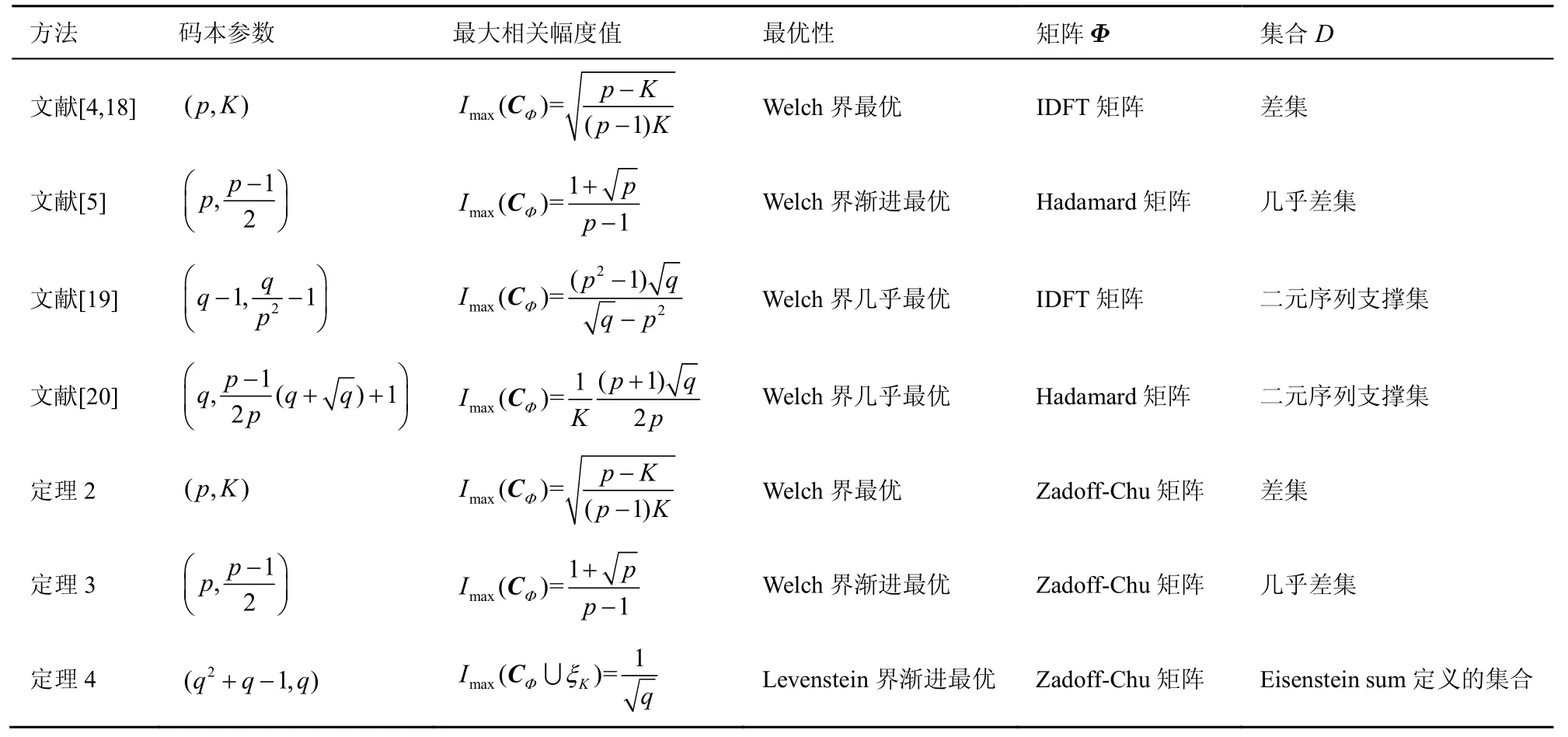
表1 幾類最優(yōu)碼本的構造方法

由表1 可以看出，根據(jù)文獻[18]提出的碼本構造框架，可以通過選取不同的變換矩陣和集合來構造不同參數(shù)的碼本。已有的方法都是基于IDFT 矩陣或Hadamard 矩陣，利用不同的集合來構造碼本。本文提出了一類新的變換矩陣，利用已有的差集、幾乎差集和有限域上的艾森斯坦和定義的一個集合構造了參數(shù)最優(yōu)和漸進最優(yōu)的碼本。定理2 和定理3 與已有的文獻[4,18]和文獻[5]中的最優(yōu)碼本具有相同的參數(shù)和最大相關幅度值，因此可以為通信系統(tǒng)或信息處理提供更多的選擇。定理4 構造出一類新的碼本，依照Levenstein 界漸進最優(yōu)，相比較依照Welch 界漸進最優(yōu)的碼本，最大互相關幅度值更小。雖然新變換矩陣放寬了限制條件使得字符集變大，但是在構造相同參數(shù)的碼本時，變換矩陣在選取上具有了更強的靈活性。在構造壓縮感知確定性測量矩陣等不要求字符集的應用中，本文構造的碼本是更好的選擇。

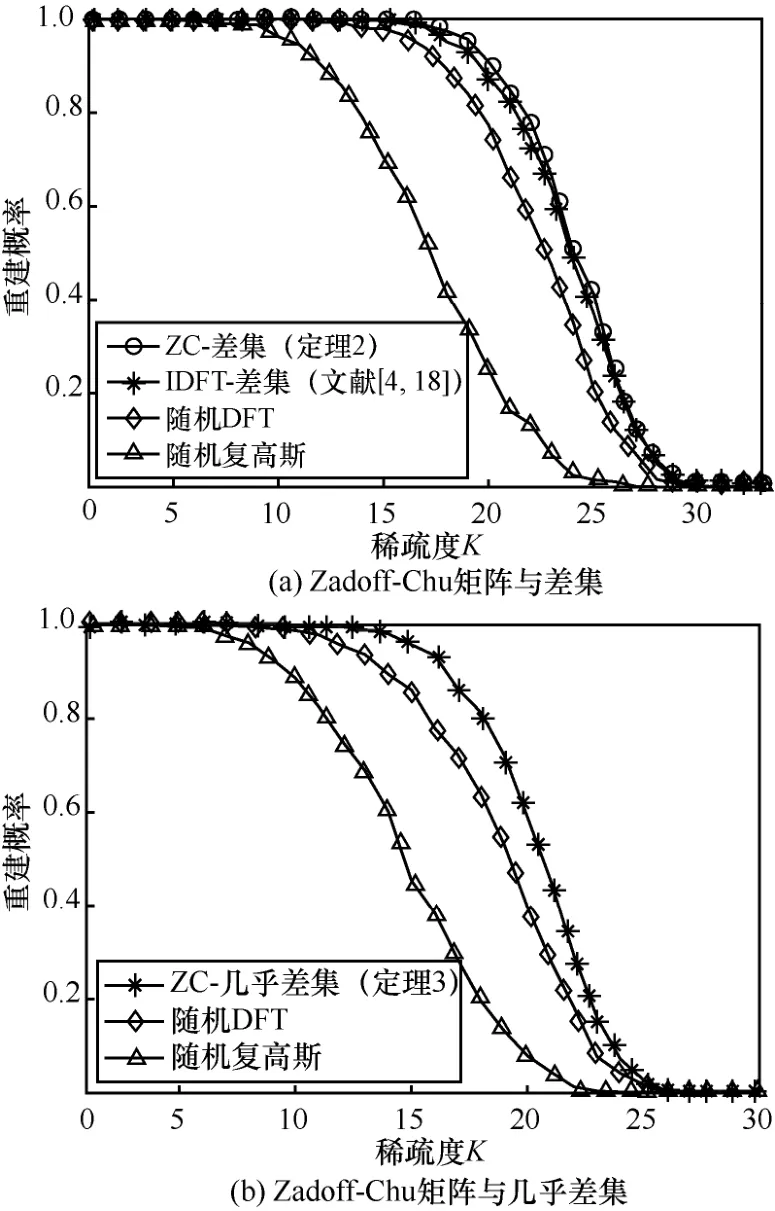
圖1 稀疏度隨重建概率變化曲線

由圖1(a)可以看出，由本文定理2 中的碼本構造的確定性測量矩陣在相同稀疏度時，重建信號的概率明顯高于隨機DFT 矩陣和隨機復高斯矩陣。利用定理2 構造出的確定性測量矩陣與利用文獻[4,18]構造的測量矩陣具有相同的參數(shù)，在重建信號的概率上甚至略高于文獻[4,18]中的方法。同理，利用本文定理3 中的碼本構造的確定性測量矩陣在重建信號的概率上明顯高于隨機測量矩陣。

6 結束語

基于文獻[18]的碼本構造思想，本文放松了變換矩陣的限制條件，提出了一類新的Zadoff-Chu 矩陣，并利用差集、幾乎差集和有限域上的特征和構造了3 類碼本，參數(shù)分別為(p,K)、和(q2+q-1,q)。本文構造的碼本與已有碼本的參數(shù)和最大互相關幅度值相同并且可以達到最優(yōu)或漸進最優(yōu)。本文方法可以為同步CDMA 通信系統(tǒng)提供大量可用碼本，并且可以通過文獻[3]的方法將本文得到的碼本應用于壓縮感知領域中確定性測量矩陣的構造，得到的確定性測量矩陣在重構信號的概率上明顯優(yōu)于隨機測量矩陣。