利用多層感知機的地震數據去噪

王琪琪 湯井田* 張 良 劉曉甲 徐志敏

(①中南大學地球科學與信息物理學院，湖南長沙 410083； ②中南大學有色金屬成礦預測與地質環境監測教育部重點實驗室，湖南長沙 410083； ③有色資源與地質災害探查湖南省重點實驗室，湖南長沙 410083； ④承德石油高等專科學校，河北承德 067000)

0 引言

由于地震勘探現場采集環境的復雜化，所得地震數據很容易混雜各種噪聲干擾，甚至會嚴重掩蓋有效信號，導致其難以分辨。因此，去噪成為地震數據處理的最重要步驟[1-3]。地震數據中噪聲主要分為隨機噪聲和相干噪聲，常用的去噪方法有奇異值分解[4-5]、小波去噪[6-7]、曲波去噪[8-10]和多項式擬合[11-12]等，其中基于稀疏變換的去噪方法因易于實施且普適性強，成為主流去噪方法。但在處理較復雜地震數據時，這類方法的去噪效果也難如人意，因此亟待探尋一種更有效的去噪方法。

近年來，隨著硬件、算法和大數據等方面的快速發展，人工智能在諸多領域得到了廣泛的應用，尤其在圖像去噪[13-14]、分類[15]和目標檢測[16]等領域已成功地解決了許多其他方法難以處理的問題。Jain等[17]用卷積神經網路對自然圖像去噪，得到了與馬爾可夫隨機模型相近或更優的結果； 并指明神經網絡模型可避免馬爾可夫模型在概率學習和推斷過程中計算復雜度較高的問題。Xie等[18]綜合稀疏編碼與深度神經網絡，提出了棧式稀疏去噪自編碼器。Burger等[19]將多層感知機用于圖像去噪，指出若訓練集足夠多，則利用MLP模型可達成當前最優的圖像去噪效果。在地震勘探領域，深度學習類方法也得到快速發展和廣泛應用，如地震數據時深轉換[20]、層析成像[21]和有效信號識別[22]等。

本文提出一種基于MLP的地震數據去噪方法：通過對已有地震數據訓練得到一個五層神經網絡模型； 用反向傳播算法調節各層神經元的權重； 然后將含噪數據作為輸入進行去噪處理并輸出結果。為了進一步驗證該方法壓制噪聲和保護有效信號的能力，選擇曲波去噪方法做對比分析。分別針對合成數據和實測地震數據進行去噪處理，結果表明本文MLP去噪方法擁有更強去噪能力，尤其在保護構造細節方面顯著優于曲波去噪方法。

1 基于MLP的地震去噪模型構建

1.1 MLP去噪機理

地震數據構成可用下式表示

x=y+n

(1)

式中：y為不含噪地震數據；n為噪聲；x為含噪地震數據。據MLP建立輸入x與輸出y之間的關系

y=H(x;θ)

(2)

式中：H表示MLP網絡結構；θ表示網絡參數的集合。地震去噪可定義為將一個含噪數據映射到一個噪聲較少的數據，為此需構建一個MLP網絡結構模型表示映射關系。

1.2 MLP網絡結構

MLP也被稱為人工神經網絡[23]或多層神經網絡，主要由輸入層(Input layer)、輸出層(Output layer)和隱層(Hidden layer)三部分構成，其中輸入層和輸出層分別只有一個，隱層可以是一層或多層拓撲結構。輸入層用于接收數據，它不進行任何計算，僅將數據按不同權重傳遞到相鄰的隱層，隱層通過非線性激活函數對數據進行處理，隨后傳遞到輸出層，最后從輸出層輸出最終結果。

一個簡單的三層感知機可表示為

f(x)=b2+W2s(b1+W1x)

(3)

式中：W1、b1分別是輸入層與隱層之間的權重矩陣和偏置矩陣；W2、b2分別是隱層與輸出層之間的權重矩陣和偏置矩陣；s是Sigmoid激活函數，能將輸入的連續實值變換為0和1之間的輸出，若是很大負數，輸出為0；若是很大正數，則輸出為1。

圖1顯示一個擁有n個輸入神經元、m個輸出神經元、q個隱層神經元的三層神經網絡。為了方便表示，將每個神經元的偏置b看作輸入為1時對應的權重的第0個分量。從該圖可見MLP中每層含有多個節點，各層的節點與下一層的節點完全連接。輸入層的節點個數表示輸入數據的維數，隱層上的節點個數與訓練數據有關，輸出層節點個數表示輸出數據的維數。

1.3 網絡訓練

訓練MLP就是利用地震數據調節其網絡參數。當MLP的輸出與地震數據的標記值(未受噪聲干擾的數據)之差達到足夠小時，可認為該MLP訓練完成。網絡的訓練一般需要循環多次，每次包含前向傳播和反向傳播兩個過程，并且采用梯度下降方式調節網絡參數。

圖1 三層感知機示意圖

y′為網絡輸出；wkj為輸入層第k個神經元與隱層第j個神經元間的權重；vji為隱層第j個神經元與輸出層第i個神經元間的權重；α和β分別是隱層和輸出層接收到的數據

1.3.1 前向傳播

以圖1所示的三層感知機為例，計算輸入為x時的網絡輸出，具體過程如下。

隱層第j個神經元接收到的輸入為

(4)

式中xk為輸入數據x在輸入層第k個神經元上的分量。通過Sigmoid激活函數，隱層對接收到的數據αj進行處理并傳遞給輸出層，則輸出層第i個神經元接收到的輸入為

(5)

網絡輸出y′由輸出層m個神經元輸出βi構成

y′=[β1,β2,…,βm]T

(6)

1.3.2 反向傳播

MLP中輸出層權重可直接用誤差更新，但隱層中不存在誤差，故對隱層不能直接用梯度下降方式調整參數，而是先將誤差通過鏈式法則反向傳播至隱層，再采用梯度下降方法處理。

由式(6)可得網絡輸出和實際輸出的均方誤差

(7)

式中yi表示實際輸出數據y在輸出層第i個神經元上的分量。誤差逆傳播算法基于梯度下降策略，以網絡的負梯度方向對權重進行調整

(8)

vji←vji+Δyji

(9)

式中η是神經網絡學習率在(0，1)間的取值。同理，其他權重系數都可通過上述反向傳播過程得到。

1.4 MLP去噪方法特點及優勢

MLP可逼近任何非線性函數，通過在大量地震數據上進行訓練更新式(2)中的θ，從而學習得到一個能表征復雜映射關系的多層網絡結構。

作為傳統的地震去噪方法，曲波變換雖然能對地震信號有較強的稀疏表示能力，但用單一的固定基難以對不同的地震信號進行最優表征。與其相比，MLP是一種數據驅動的地震去噪方法，它可根據訓練樣本提取地震信號的本質特征，從而自適應地對地震信號進行表征。

2 實驗設置

2.1 數據集劃分和標記

選擇SEG(勘探地球物理學家協會)官網提供的地震數據集，其中包含二維數據和三維數據。

針對三維地震數據，將其沿剖面展開為多個二維數據。因相鄰三道地震信號有很強的相似性，每隔三道選取一組二維數據[24]。為了降低地震數據類型對網絡泛化能力的影響，本文使用同一方式生成訓練集、測試集和驗證集數據，且陸地和海洋地震數據的占比相同。考慮到神經網絡對噪聲類型不敏感，向不含噪的三種數據集摻入隨機噪聲和脈沖噪聲作為樣本標簽，含此兩種噪聲的樣本各占50%。

2.2 數據預處理

不同地震數據的取值范圍不同，應在輸入網絡前對其進行歸一化以消除相關影響。網絡的輸入神經元個數是確定的，需對不同道集和不同采樣時間的地震數據進行分割或零值填充。

2.3 超參數

超參數是網絡訓練前設置的參數，包括隱層層數、神經元個數和學習率等。超參數對訓練結果有很大影響，如學習率的不同會改變網絡收斂速度。本文構建模型的隱層個數按照Burger等[19]的方法設置，其他參數據驗證集誤差手動調節(表1)。

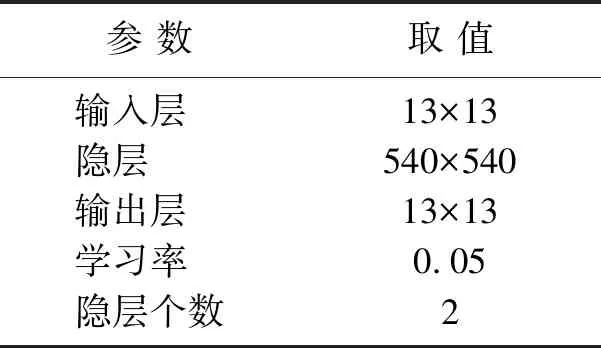
表1 模型參數

2.4 驗證集結果分析

在網絡訓練過程中，驗證集用于調整超參數。根據不同模型在驗證集上的表現決定所要選擇的超參數； 同時，驗證集也用于監控模型是否發生“過擬合”。據圖2所示誤差曲線可評估所構建模型是否處于“過擬合”或“欠擬合”。

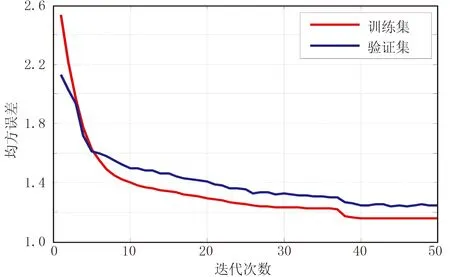
圖2 驗證集和訓練集的均方誤差隨迭代次數的變化

從圖2可見： 訓練集和驗證集的誤差曲線總體上隨迭代次數增加呈下降趨勢； 前6次迭代誤差曲線的下降速度很快，之后下降速度逐漸減小； 在第37次迭代又出現了一次較明顯下降，此后隨迭代次數的繼續增加誤差趨于不變，此時訓練集和驗證集上各自的相對誤差都很低，且這二者十分接近，表明模型具有較好的泛化能力。

3 模型數據測試

選取已訓練好的MLP模型對合成數據進行去噪，所含噪聲為高斯白噪聲。作為對比，同時采用曲波變換法做去噪處理。以通用的信噪比表征法評判MLP方法的去噪效果

(10)

式中RS/N為信號與噪聲強度的比值(dB)，此處y和y′分別指原始的和去噪后地震數據。

3.1 MLP對高斯白噪聲的壓制

圖3a為均勻背景中嵌入一個正方形的簡單模型： 背景區域尺寸為256×256，其數據值為10； 正方形尺寸為100×100，其數據值為100。在相應的頻率—波數域圖像(圖3d)上，發現其能量主要集中為“十字型”。但在加入隨機噪聲后(圖3b，信噪比為6.3dB)的頻率—波數域分布上，部分頻率—波數域信息被隨機噪聲混雜而難以識別(圖3e)，特別是能量相對較弱的“十字型”末端，幾乎無法分辨。在采用MLP去噪后的時間域(圖3c)和頻率域(圖3f)圖像上，隨機噪聲得到較好壓制，在噪聲與有效信號難以分辨處也取得很好效果。

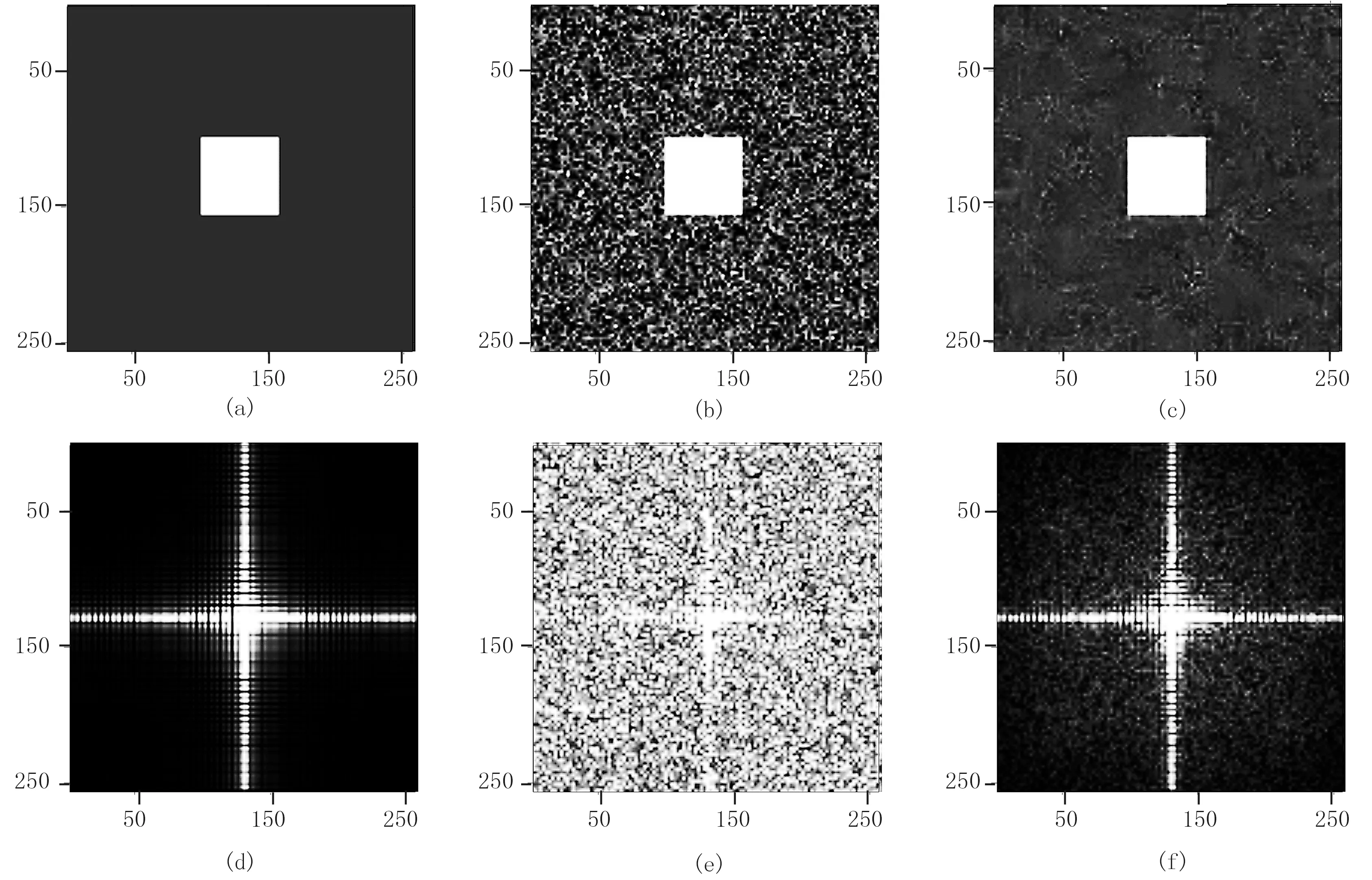
圖3 MLP去噪效果

3.2 合成數據去噪

圖4a所示原始地震數據共有100道，采樣點數為512，采樣率為1ms，圖中構造復雜區(能量集中)位置用紅框做了標示。向該數據加入高斯白噪聲(圖4b)，其信噪比變為4.25dB。對該含噪數據做曲波去噪處理(圖4c)，所得結果與含噪數據差值(圖4d)的信噪比為8.22dB，比原含噪數據提高了3.97dB。但可見部分復雜構造區依舊存在噪聲，尤其在圖4d紅框標示處明顯殘存一些有效信號(將部分信號當作噪聲濾除)，因此曲波方法去噪效果欠佳。采用MLP去噪后(圖4e)的信噪比增至12.62dB，顯然MLP方法對噪聲去除得更徹底，對構造細節的保護也更強，整體上與原始信號更接近。

針對原始合成數據加入強度分別為1，2，…，7dB的噪聲，計算不同強度噪聲下去噪結果的信噪比(圖5)。可見兩種方法去噪結果的信噪比都隨含噪數據信噪比的增大而增大，其中MLP去噪效果明顯好于曲波法，在3～5dB范圍信噪比差值達到最大，且在強噪聲下MLP方法仍能取得很好效果，表明該方法在不同噪聲強度下去噪效果穩定。

3.3 復雜數據去噪

圖6a所示的陸地地震數據共有128道，每道采樣點為256個。相比于合成數據，其構造更復雜，存在較多斷點； 對其加入高斯白噪聲后(圖6b)，信噪比為4.05dB。采用曲波去噪后(圖6c)雖較好地重構了有效信號，但在紅框標示的同相軸頂部仍存在較多噪聲(圖6d)，難以有效識別周圍數據。而采用MLP方法在壓制噪聲(圖6e)的同時，同相軸的輪廓更清晰，斷點附近的構造細節也得到了很好保護，如在紅框標示區更易識別同相軸邊界(圖6f)。

圖4 合成數據去噪結果

圖5 合成數據去噪結果信噪比隨噪聲強度的變化

圖7是不同噪聲強度下陸地地震數據去噪后的信噪比折線圖。可見當處理存在較多復雜構造的數據時，MLP方法去噪結果的信噪比明顯高于曲波法，雖然在1～3dB范圍MLP方法去噪效果未明顯改善，但仍比曲波好。

圖8a為原始海洋數據的灰度顯示，共有128道，采樣點數為256，采樣率為1ms。相比于陸地數據，其 紋理結構簡單且多為直線。加入噪聲后(圖8b)，其信噪比為3.19dB，噪聲使得部分紋理不清晰，對一些能量弱的同相軸已無法分辨。

圖6 陸地地震數據去噪結果

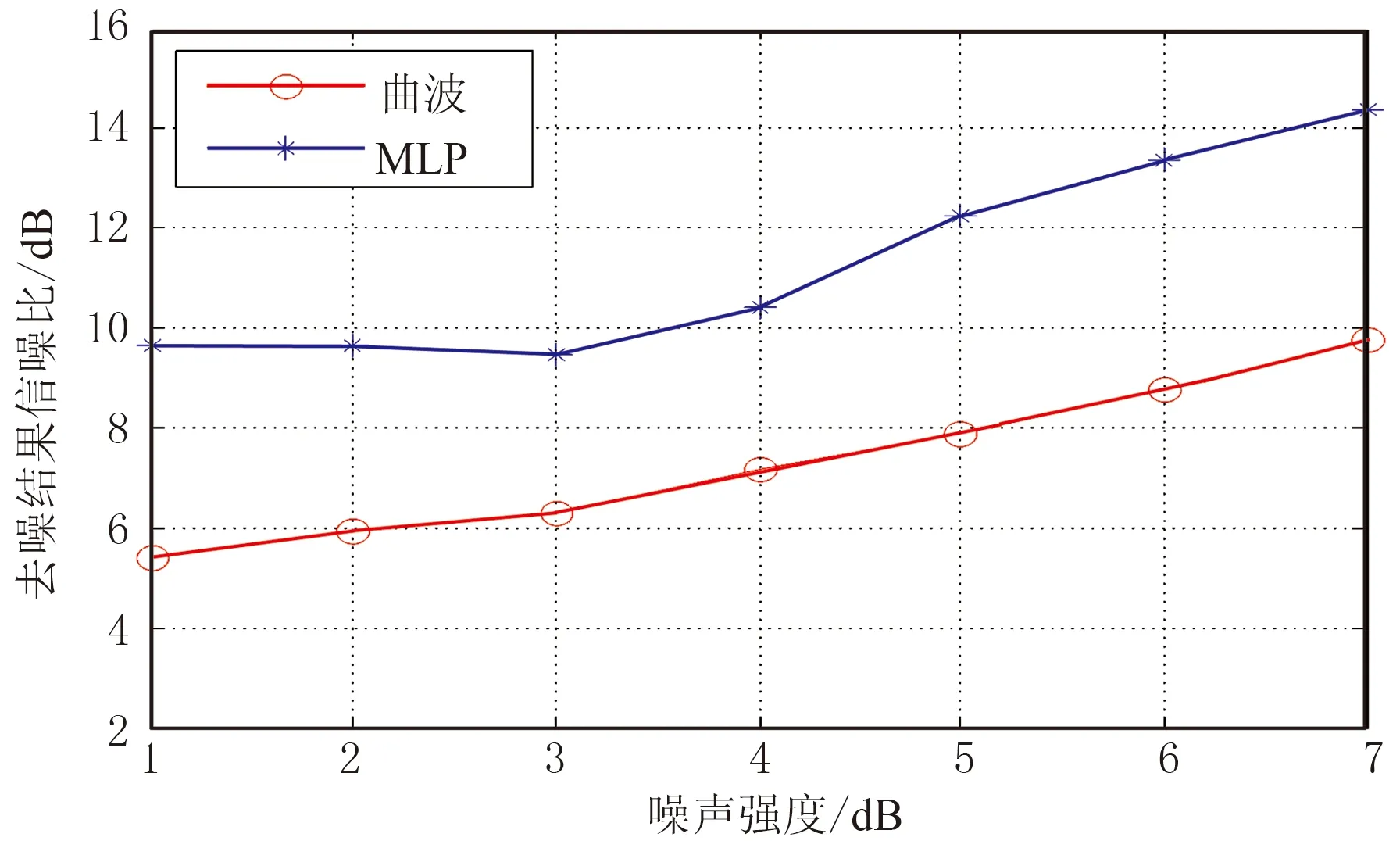
圖7 陸地數據去噪結果信噪比隨噪聲強度的變化

從曲波法(圖8c)和MLP(圖8e)去噪結果看，對于能量較強的同相軸，兩種方法都取得了較好去噪效果。但對紅框標示的能量較弱的同相軸而言，曲波法未能很好地重構這些數據，從差值(圖8d)也可見曲波法去噪后仍存有較多噪聲，甚至一些有效信號也被壓制； MLP去噪結果(圖8e)展示了更清晰的地層結構，同相軸連續性更好，其差值(圖8f)顯示去噪徹底、干凈。

圖9展示了不同噪聲強度下海洋數據的信噪比折線圖。顯然MLP方法去噪結果的信噪比高于曲波法，且與前面合成數據(圖5)和陸地地震數據(圖7)的去噪結果顯示類似，兩種方法的去噪結果的信噪比與含噪數據的信噪比呈正相關。

圖8 海洋地震數據去噪結果

3.4 壓制非高斯脈沖噪聲

前面主要介紹了MLP方法對高斯白噪聲的去噪效果，但考慮到實際地震數據中存在多種類型噪聲，這里以脈沖噪聲為例進一步驗證MLP方法對非高斯類噪聲的壓制能力。

圖10所示的地震數據共有100道，采樣點為256個，主要由三個較強能量的同相軸組成。加入脈沖噪聲后地震數據(圖10b)的信噪比為10.65dB。從其曲波法去噪結果(圖10c)上可見仍存在很多脈沖噪聲，去噪效果顯然不理想； 采用MLP方法去噪后(圖10d)，很好地壓制了脈沖噪聲，三個同相軸的邊界很清晰，且其能量幾乎未被減弱，信噪比增至21.01dB。

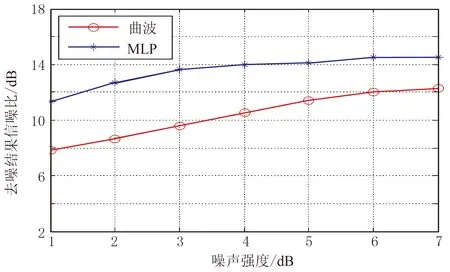
圖9 海洋數據去噪結果信噪比隨噪聲強度的變化

圖10 脈沖噪聲去噪結果

4 實際地震數據處理

針對M地區實際陸地地震數據進行測試。截取的部分實測地震數據(圖11a)共有160道，采樣點為2500個，可見其中含有較強隨機噪聲，能量較弱的有效信號被壓制。

為了更好地對比曲波(圖11b)和MLP(圖11c)的去噪效果，對圖中紅框標示區域進行放大，并繪制了如圖12所示的波形變面積圖。發現曲波和MLP去噪方法都削弱了噪聲影響，但曲波法去噪結果中仍殘留較多隨機噪聲，影響了對部分弱地震信號的識別(圖12b)，去噪效果欠佳； 而MLP方法對隨機噪聲的壓制更徹底，且更充分地保護了能量弱的地震信號(圖12c紅色箭頭所示)。

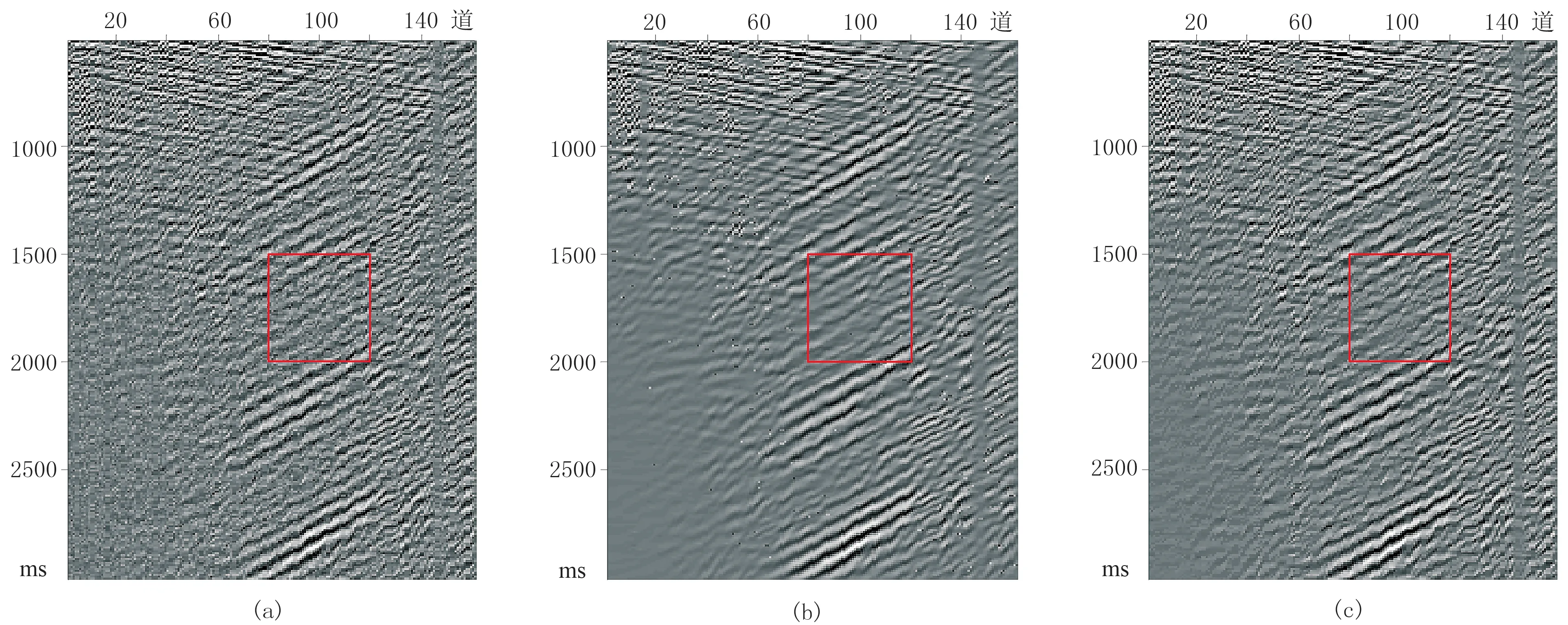
圖11 實際地震數據去噪結果

圖12 實測數據波形變面積圖

5 結論與討論

本文主要介紹了基于MLP的去噪方法，針對不同類型(含噪)地震數據對比分析了MLP方法的去噪能力，得到了如下結論：相比于曲波變換法，MLP方法在壓制噪聲的同時能有效保護原始數據，對一些構造復雜區域能實現很好地重構；對不同信噪比數據，MLP方法處理效果更穩定，且對脈沖噪聲等非高斯類噪聲也有較好壓制效果。

盡管MLP方法已取得較好去噪效果，但本文僅對高斯噪聲和非高斯脈沖噪聲進行了處理，而對地震信號中其他噪聲，如有色噪聲和時空變隨機噪聲等，未做相關研究和去噪處理，不能預判MLP方法的效果。因此，今后將致力于對實際地震數據中存在的其他各類噪聲的壓制。