一類具有非單調(diào)傳染率的隨機(jī)SIQR傳染病模型的動(dòng)力學(xué)分析
馬苓涓,張?zhí)祝钪久?/p>
(長(zhǎng)安大學(xué)理學(xué)院,陜西 西安 710064)
傳染病的流行與爆發(fā),是當(dāng)今人類社會(huì)面臨的重大挑戰(zhàn)之一。在人類文明史上,傳染病曾經(jīng)帶來(lái)過巨大的災(zāi)難。在近現(xiàn)代,也給人類生命和財(cái)產(chǎn)造成了無(wú)可挽回的損失[1]。為了更好地預(yù)防和控制傳染病,學(xué)者們通過建立數(shù)學(xué)模型對(duì)傳染病進(jìn)行研究。
目前研究表明,有些傳染病,需要對(duì)感染疾病的個(gè)體進(jìn)行隔離治療,因此具有隔離策略的傳染病模型受到廣泛關(guān)注。Joshi等[2]分析了一個(gè)飽和發(fā)病率與檢疫隔離相結(jié)合的SIQR傳染病模型,給出了模型的閾值,平衡點(diǎn)的存在性及其穩(wěn)定性。在文獻(xiàn)[3-5]中,作者研究了具有非線性傳染率的SIQ傳染病模型,并證明了無(wú)病平衡點(diǎn)和地方病平衡點(diǎn)是全局穩(wěn)定的。另一方面,學(xué)者也研究了具有隨機(jī)擾動(dòng)的傳染病模型。Yang等[7]考慮了隨機(jī)SIR及SEIR傳染病模型解的全局正性,并得到了關(guān)于相應(yīng)的確定性系統(tǒng)的無(wú)病平衡點(diǎn)及地方病平衡點(diǎn)的漸近行為。武麗鳳等[8]研究了具有比率依賴的食餌-捕食隨機(jī)模型,分析了系統(tǒng)趨于滅絕及平均持久的條件。因此,從上述研究中可以看出,具有隔離策略的隨機(jī)傳染病模型是一個(gè)仍要解決的問題。
May[10]曾指出:當(dāng)考慮到環(huán)境的噪音時(shí),模型的參數(shù)將會(huì)展現(xiàn)出隨機(jī)擾動(dòng)。在文獻(xiàn)[6-7,9]的基礎(chǔ)上,我們建立以下一類隨機(jī)SIQR傳染病模型:
(1)
上式模型(1)對(duì)應(yīng)的確定性模型如下:
(2)
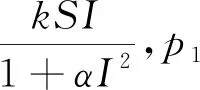
本文研究?jī)?nèi)容安排如下:第一節(jié),給出隨機(jī)模型(1)正解的全局存在唯一性。第二節(jié),討論隨機(jī)模型(1)的解在無(wú)病平衡點(diǎn)的擾動(dòng)行為。第三節(jié),研究疾病的滅絕性。第四節(jié),給出隨機(jī)模型(1)的解在地方病平衡點(diǎn)存在唯一的平穩(wěn)分布的充分條件。第五節(jié),數(shù)值模擬顯示了模型的動(dòng)力學(xué)形態(tài)。最后,對(duì)文章進(jìn)行了總結(jié)。
1 全局正解的存在唯一性
首先,我們需要給出模型的適定性,本節(jié)通過構(gòu)造適當(dāng)?shù)腖iapunov函數(shù)并利用停時(shí)理論來(lái)證明隨機(jī)模型(1)正解的全局存在唯一性。
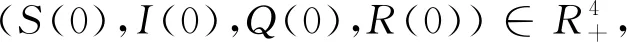
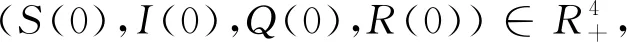
τn=inf{t∈[(0,τe):S(t)≥n;I(t)≥n;Q(t)≥n;R(t)≥n}
定義以下Liapunov函數(shù)
V(S,I,Q,R)=S+I+Q+R
由伊藤公式[11]得
dV(S,I,Q,R)=LVdt+σ1SdB1(t)+σ2IdB2(t)+σ3QdB3(t)+σ4RdB4(t)≤
Adt+σ1SdB1(t)+σ2IdB2(t)+σ3QdB3(t)+σ4RdB4(t)
(3)
其中
LV(S,I,Q,R)=A-dS-(d+p1)I-(d+p2)Q-dR
對(duì)于任意的n≥n0,存在常數(shù)T≥0使得τn∈(0,τn∧T)。現(xiàn)對(duì)(3)兩端從0到τn∧T積分并求期望可得
EV(S(τn∧T),I(τn∧T),Q(τn∧T),R(τn∧T))≤V(S(0),I(0),Q(0),R(0))+AT

這就說明在[0,∞)內(nèi)(S(t),I(t),Q(t),R(t))以概率1在有限時(shí)間內(nèi)不會(huì)產(chǎn)生爆破。
2 無(wú)病平衡點(diǎn)E0的漸近行為
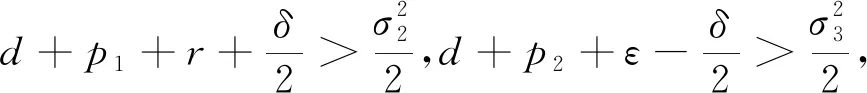
其中
證明定義如下的Liapunov函數(shù):
V(S,I,Q,R)=V1+c1V2+V3+c2V4+c3V5
(4)
其中
(5)
根據(jù)伊藤公式得
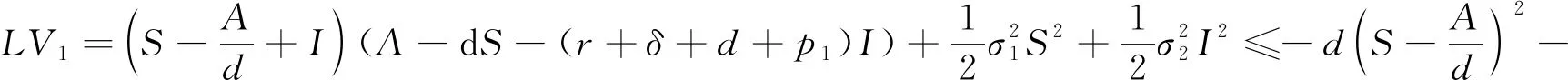
(6)
由式(4)~式(6)可得
其中
r+δ+2d+p1-c1k=0,c1(r+δ+d+p1)(1-R0)-c2δ-c3r=0,c2(ε+d+p2)-c3ε=0
則有
由上式可以得出
(7)
對(duì)式(7)兩端從0到t積分并求期望得
上式兩端同時(shí)除以t,再令t→∞可得
證畢。
根據(jù)定理2知,在滿足某些條件下,證明了隨機(jī)模型(1)的解將在確定性模型(2)的無(wú)病平衡點(diǎn)E0附近振蕩,并且擾動(dòng)強(qiáng)度與σi(i=1,2,3,4,5)有關(guān)。
3 隨機(jī)滅絕性
在傳染病模型中,更關(guān)心的是在什么情況下疾病會(huì)滅絕,本節(jié)指出當(dāng)外界干擾強(qiáng)度較大時(shí)能導(dǎo)致疾病滅絕,即大噪聲能導(dǎo)致疾病滅絕。
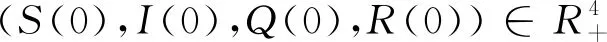
(8)
更多的有
(9)
和
(10)
證明由模型(1)可以得到
d(S+I+Q+R)=[A-d(S+I+Q+R)-p1I-p2Q]dt+σ1SdB1+σ2IdB2+σ3QdB3+σ4RdB4
(11)
對(duì)式(11)兩端分別從0到t積分得
(12)
其中
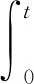
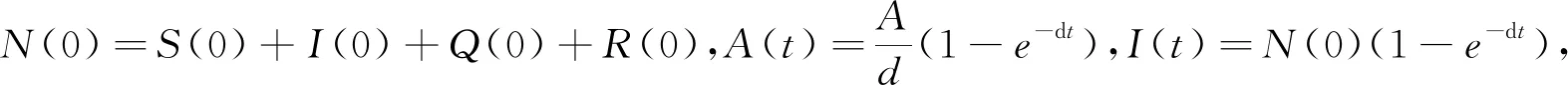
令
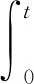
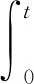
于是
(13)
由鞅的強(qiáng)大數(shù)定律[11]和式(13)得
由(8)可得
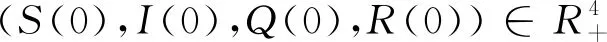
其中
這里
b=ε(δ+r+d+p1),c=(ε+d+p2)(r+d+δ+p1)
證明令W(t)=aI(t)+bQ(t)+cR(t),利用伊藤公式得
(14)
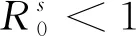
即推出
(15)
另一方面,有(11)可以得到
相當(dāng)于
(16)
其中
由式(9)和式(10)得
(17)
更多地由式(15),式(16)和式(17)可以得到
證畢。
4 地方病平衡點(diǎn)E*的附近的平穩(wěn)分布
引理5[13]Markov過程X(t)存在遍歷的平穩(wěn)分布π(·)。如果存在具有正則邊界?U的有界集合U?Rd滿足如下性質(zhì):
A1:存在鄰域U及其某鄰域,擴(kuò)散矩陣A(x)的最小特征值是非零的;
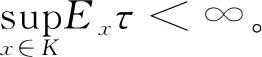
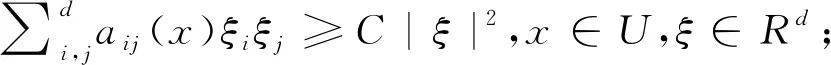
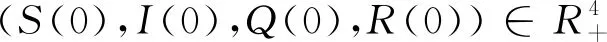
bi>0(i=1,2,3,4),B 成立,則模型(1)存在遍歷的平穩(wěn)分布[16]。 其中 證明為了證明定理6,我們需要滿足引理5中的條件A1和A2,接下來(lái),先證明A1。當(dāng)R0>1時(shí),模型(2)存在唯一的地方性平衡點(diǎn)E*=(S*,I,*Q*,R*),且滿足 則模型(1)在地方病平衡點(diǎn)(S*,I*,Q*,R*)的擴(kuò)散矩陣為 條件A1已經(jīng)滿足.接下來(lái)證明條件A2,定義Liapunov函數(shù) (18) 其中 (19) 根據(jù)伊藤公式以及2ab≤a2+b2得 (20) 由式(18)~式(20)得 LV≤-b1(S-S*)2-b2(I-I*)2-b3(Q-Q*)2-b4(R-R*)2+B 因此,橢球 b1(S-S*)2+b2(I-I*)2+b3(Q-Q*)2+b4(R-R*)2=B LV(S,I,Q,R)<0 證畢。 因此,引理5的條件已經(jīng)滿足,我們也可以得到模型(2)的正解在地方病平衡點(diǎn)E*附近存在一個(gè)遍歷平穩(wěn)分布。 本節(jié)我們利用計(jì)算機(jī)模擬出確定性模型和隨機(jī)模型中染病者的曲線,來(lái)說明噪聲對(duì)確定性模型的影響。 (1)選取初值(S(0),I(0),Q(0),R(0))=(0.5,0.2,0.1,0.1),參數(shù):A=0.5,k=0.3,d=0.2,α=0.2,r=0.3,δ=0.3,p1=0.3,ε=0.2,p2=0.25,σ1=0.8,σ2=0.5,σ3=0.5,σ4=0.5,σ5=0.6,此時(shí)R0=0.7467<1,并且滿足定理2的條件,則模擬結(jié)果如圖1所示。由圖可知,當(dāng)隨機(jī)干擾的強(qiáng)度較大時(shí),系統(tǒng)(1)的解總是在無(wú)病平衡點(diǎn)處振動(dòng),這表明疾病會(huì)消亡。 (2)選取初值(S(0),I(0),Q(0),R(0))=(2,1.8,1.3,1.2),參數(shù):A=2.5,k=0.4,d=0.3,α=0.1,r=0.2,δ=0.2,p1=0.3,ε=0.2,p2=0.2,σ1=0.01,σ2=0.01,σ3=0.01,σ4=0.01,σ5=0.01,此時(shí)R0=3.333 3>1,并且滿足定理6的條件,則數(shù)值模擬如圖2所示。由圖可知,當(dāng)隨機(jī)干擾的強(qiáng)度較小時(shí),系統(tǒng)(1)的正解在地方病平衡點(diǎn)存在一個(gè)平穩(wěn)分布,這表明疾病會(huì)一直存在。 由于現(xiàn)實(shí)世界中的大多數(shù)問題都是不確定性的,將隨機(jī)效應(yīng)引入到模型(2)中,為傳染病模型的建模提供了一種更為現(xiàn)實(shí)的方法。 我們的工作為隨機(jī)微分方程為傳染病動(dòng)力學(xué)建模提供了另一種見解,它顯示了對(duì)這個(gè)特殊問題的不同看法。特別地,我們得到了隨機(jī)系統(tǒng)的遍歷性。因此,接下來(lái)可以進(jìn)一步考慮隨機(jī)系統(tǒng)的穩(wěn)定性。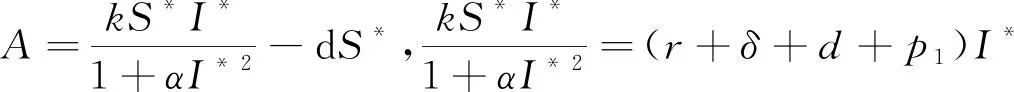
5 數(shù)值模擬
6 結(jié)論


