狀態(tài)依賴時(shí)滯的非局部擴(kuò)散方程的行波解存在性

王 治，萬(wàn)育基，余志先

（1.上海理工大學(xué) 理學(xué)院，上海 200093；2.上海師范大學(xué) 數(shù)理學(xué)院，上海 200234）

1 問(wèn)題的提出

雖然狀態(tài)依賴時(shí)滯的微分方程（SD-DDE）可以追溯到19 世紀(jì)，但該類型方程研究由于在各種情況下的頻繁運(yùn)用而再一次成為研究熱點(diǎn)，見(jiàn)文獻(xiàn)[1-4]。

Lv 等[3]研究了一種狀態(tài)依賴時(shí)滯的擴(kuò)散階段結(jié)構(gòu)模型，并得到了大波速下的行波解的存在性。Lin 等[4]進(jìn)一步研究了狀態(tài)依賴時(shí)滯的反應(yīng)擴(kuò)散方程：

的行波解的存在性，其中u(x,t)代表時(shí)刻t在x處的種群密度。

行波解的概念在1937 年由Kolmogorov 等[5]提出，用來(lái)解釋動(dòng)物基因的傳播過(guò)程。行波解現(xiàn)象不僅存在于種群模型中，也存在于物理、化學(xué)、生物及神經(jīng)網(wǎng)絡(luò)等領(lǐng)域，見(jiàn)文獻(xiàn)[3-5]。行波解也可以用來(lái)解釋自然界中傳播和震動(dòng)現(xiàn)象，因而具有重要的實(shí)際意義。

盡管方程（1）中Laplacian 擴(kuò)散模型應(yīng)用廣泛，但它表示的生態(tài)系統(tǒng)的一個(gè)重要缺點(diǎn)是這種擴(kuò)散是一個(gè)局部擴(kuò)散，這表明種群中的個(gè)體只能影響到局部范圍。克服這類問(wèn)題的常用方法是用卷積算子或積分微分方程來(lái)研究擴(kuò)散系統(tǒng)，見(jiàn)文獻(xiàn)[6-7]。Wan 等[8]研究狀態(tài)依賴時(shí)滯的非局部的種群模型

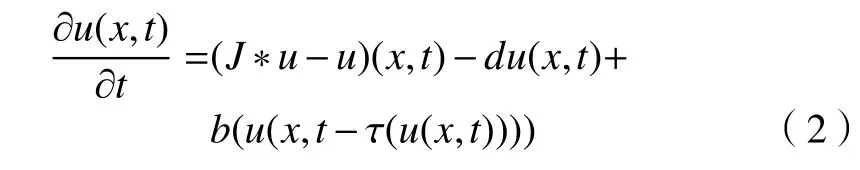
的行波解的存在性，其中u(x,t)代表在時(shí)刻t位置x處的種群密度，J*u-u是 一個(gè)非局部擴(kuò)散算子，定義為若J(x-y)是從y位置跳躍到x位置的概率分布，則J*u代表個(gè)體從所有其他位置到x位置的種群數(shù)量，并且u(x,t)=代表從x位置處到其他位置的種群數(shù)量。在種群模型中，d為死亡率，b(u)為出生函數(shù)，τ(u)為種群密度依賴的成熟時(shí)滯。

本文考慮更一般的非局部帶狀態(tài)依賴時(shí)滯反應(yīng)的擴(kuò)散系統(tǒng)的行波解的存在性，方程如下

方程（3）的行波解，是一種定義在全空間上特殊的整體解，且具有如下形式：u(x,t)=φ(ξ),ξ=x+ct，

其中c＞0為波速，φ∈C1(R,R)為波像函數(shù)并滿足方程

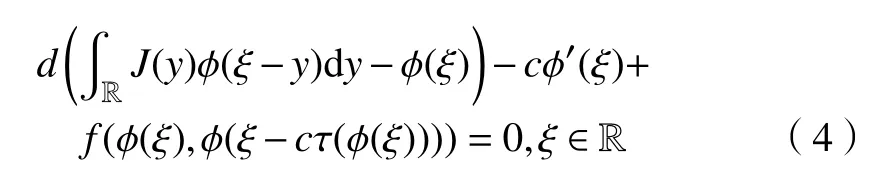
和漸近邊界條件

特別地，稱滿足條件（5）的單調(diào)行波解為波前解。

2 主要結(jié)果

現(xiàn)在給出一些假設(shè)：

定理1假設(shè)a～e 成立，存在一個(gè)正常數(shù)c*，當(dāng)c≥c*時(shí)，方程（4）存在一個(gè)非減的正的行波解u(t,x)=φ(x+ct)，且φ(-∞)=0,φ(+∞)=K。此外，

其中，λ1＞0為下列方程的最小實(shí)根。

3 主要結(jié)果的證明

問(wèn)題（3）行波解的存在性的證明，將分成3 個(gè)部分來(lái)完成。首先，利用合適的上下解及有關(guān)假設(shè)構(gòu)造一個(gè)算子所在集合 Γ；其次，證明定義的算子F:Γ→Γ在Bλ中關(guān)于范數(shù)‖·‖Bλ全連續(xù)；最后，利用Schauder 不動(dòng)點(diǎn)定理，得到存在性定理。

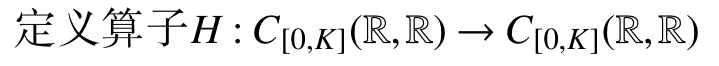
其中，β ＞d，C[0,K](R,R)={φ∈C(R,R)|0 ≤φ(ξ)≤K,ξ∈R}。進(jìn)一步定義算子F:C[0,K](R,R)→C[0,K](R,R)

顯然，算子F的一個(gè)不動(dòng)點(diǎn) φ就是方程（4）的解，即

因此，為了研究方程（4）解的存在性，只需研究算子F的不動(dòng)點(diǎn)的存在性。

因?yàn)?2f(u,v)≥0,(u,v)∈[0,K]2，容易知道函數(shù)f滿足如下擬單調(diào)條件。

引理1假設(shè)a～c 成立，存在一個(gè)正常數(shù)β ＞使得

其 中，φ1,φ2∈C[0,K](R,R)，且 當(dāng)ξ∈R,0 ≤φ2(ξ)≤φ1(ξ)≤K。

引理2假設(shè)a～d 成立，如果φ∈C[0,K](R,R)，對(duì)于任何c＞0，則有

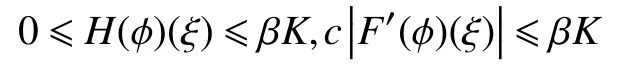
證明易證0 ≤H(φ)(ξ)≤βK。由算子F的定義，有

故得證。

現(xiàn)在，引入積分方程（9）的上下解的概念。

定義1一個(gè)連續(xù)有界的函數(shù)φ:R→[0,K]稱為方程（9）的一個(gè)上解當(dāng)且僅當(dāng)滿足如下條件：

方程（9）的一個(gè)下解也可以類似定義得到，只需將式（10）不等號(hào)反向。

當(dāng)λ≥0,c≥0，定義一個(gè)函數(shù)Δ(c,λ)如下：

引理3假設(shè)a～d 成立，則存在唯一的c*＞0滿足如下條件：

①若c≥c*，則存在兩個(gè)正數(shù)0 ＜λ1≤λ2，Δ(c,λ1)=Δ(c,λ2)=0；

②若c＜c*，則對(duì)所有λ ＞0，Δ(c,λ)＜0；

③若c=c*，則 λ1=λ2=λ*，當(dāng)c＞c*，則 λ1＜λ*＜λ2，

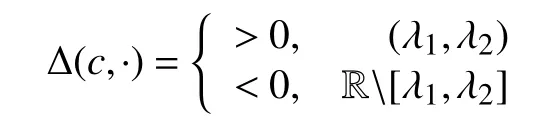
對(duì)于在引理3 中給定的常數(shù)c＞c*和λ1,λ2，定義連續(xù)函數(shù)[9-11]：

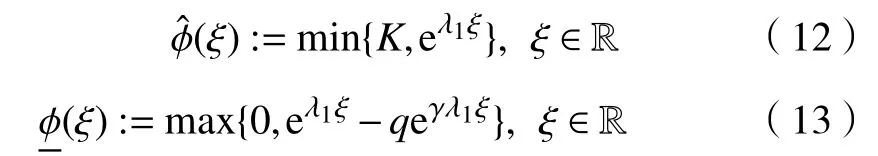
引理4假設(shè)a～d 成立，則對(duì)波速c＞c*，此時(shí)，存在一個(gè)β1＞0，當(dāng)β ≥β1，ξ1,ξ2∈R時(shí)，

證明注意到

令β1=L1，即完成證明。

引理5假設(shè)a～d 成立，當(dāng)波速c＞c*，與分別為方程（9）的一個(gè)上解和下解。

證明因?yàn)閷?duì)ξ∈R，0 ≤φ?(ξ)≤K，由引理1 知

且有

則

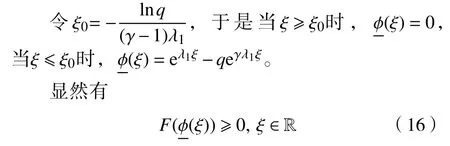
由假設(shè)條件e，存在δ1,δ2＞0,0 ＜L＜∞，當(dāng)(u,v)∈[0,κ]2，使得

易知存在一個(gè)Q1(γ)?1，當(dāng)q≥Q1(γ)，有eλ1ξ-qeγλ1ξ≤κ。因此，0 ≤φ(ξ)≤κ。因?yàn)棣?＜0，1+σi＞γ,i=1,2，故可得

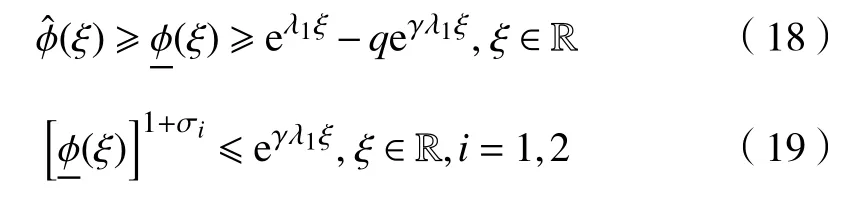
根據(jù)式（18）和式（19），可得

由式（20）得

結(jié)合式（16）和式（21），有

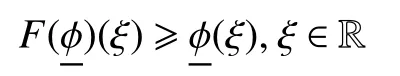
下面，將要通過(guò)Schauder 不定點(diǎn)定理來(lái)尋求算子F的不動(dòng)點(diǎn)。為此，可以引進(jìn)指數(shù)衰減范數(shù)。當(dāng)0 ≤λ ≤λ1，定義

容易驗(yàn)證Bλ(R,R)是一個(gè)附有范數(shù)的一個(gè)Banach 空間。

易證集合Γ為非空、有界、閉凸集。對(duì)于在式（8）中定義的算子F，有如下引理成立。

引理6假設(shè)a～e 成立，

①F(Γ)?Γ;

②F:Γ→Γ在Bλ中關(guān)于范數(shù)‖·‖Bλ是全連續(xù)。

證明根據(jù)引理1～5，對(duì)任意φ∈Γ，有

且F(φ)(ξ)關(guān)于φ(ξ)∈C[0,K](R,R)是非減的，c|F′(φ)(ξ)|≤βK。因此，F(xiàn)(Γ)?Γ。

因f∈C1([0,K]2,R)，存在M＞0，滿足|f(u1,v1)-f(u2,v2)|≤M(|u1-u2|+|v1-v2|)，其 中ui,vi∈[0,K],i=1,2。于是，對(duì)φ,ψ∈Γ，有

因此，可得

它表明F:Γ→Γ在Bλ(R,R)中關(guān)于范數(shù)‖·‖Bλ是連續(xù)的。另一方面，對(duì)任意φ∈Γ，ξ∈R，當(dāng)ξ1≥ξ2，ξ1,ξ2∈R時(shí)，

這表明對(duì)于ξ∈R，{F(φ)(ξ):φ∈Γ}是一致有界并且等度連續(xù)。因此，通過(guò)Arzela-Ascoli 定理，對(duì)于在F(Γ)中任意給定的序列{ψn}n∈N，存在nk→∞和 ψ∈C(R,R)，使得在 R任何緊支集上(ξ)=ψ(ξ)關(guān)于 ξ一致成立。因?yàn)椋瑢?duì)任意的，于是有即ψ(ξ)∈Γ。另外有

因此，對(duì)任意ε ＞0，可以找到M0＞0，使得對(duì)任意的|ξ|≥M0，可得

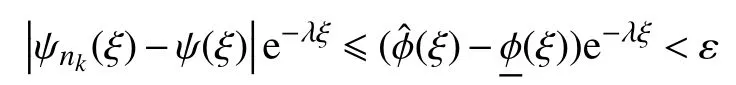
此外，當(dāng)|ξ|≤M0時(shí)，一致存在，于是存在k*＞0，當(dāng)k≥k*時(shí)，對(duì)任意的|ξ|≤M0，可得

由此可得，當(dāng)k→∞時(shí)，所以，F(xiàn):Γ→Γ在Bλ中關(guān)于范數(shù)‖·‖Bλ全連續(xù)。

定理1 的證明。

證明根據(jù)引理6 和Schauder 不動(dòng)點(diǎn)定理，F(xiàn)存在一個(gè)不動(dòng)點(diǎn)φ∈Γ。因φ(ξ)非減且有界，所以。由洛必達(dá)法則，可得

定理1 得證。