基于效用分類的智能電網實時電價算法

原冠秀，高 巖，王宏杰

（1.上海理工大學 管理學院，上海 200093；2.上海健康醫學院 文理學院，上海 201318）

隨著現代工業技術的快速發展，人類生活變得越來越方便，如智能家居、電動汽車等的使用。然而，方便的同時也給世界能源可持續發展帶來了巨大的挑戰，尤其越來越多的電器產品和工業的超負荷運營，是當前世界電網所面臨亟待解決的問題。在這種背景下，智能電網應運而生，智能電網是連接發電廠、供電商、用戶之間的依靠先進的通信和計量設施建立起來的電力網絡結構。

1 研究背景

由于電力能源自身的易損性和難存儲性，要求電力市場供電側和需求側達到均衡時，才能實現能源的利用最大化。在電力市場運營中，實時電價已經是智能電網需求側管理的重要手段之一。在實時電價問題的解決過程中，目前國內外研究主要采用兩種方法：一種是利用博弈論方法均衡供電側和需求側之間的關系，制定定價機制；另一種是利用最優化方法研究社會福利最大化問題[1-2]。現有利用最優化方法來研究實時電價的文獻，大多數考慮的是用戶效用函數為單一類型，而現實生活中，由于用戶種類繁多，他們的消費模式和偏好不同，效用函數會呈現多樣化。文獻[3]研究了基于用戶效用最大化和供電商成本最小化的社會福利最大化模型，通過分布式算法進行對偶分解，并利用梯度投影法給出了供電商與用戶之間的實時電價更新算法。文獻[4-5]討論了不同環境中智能電網實時電價的需求側管理，提出了一些啟發式算法，解決供電商和用戶之間的用電策略，如粒子群算法、模擬退火法、ADMM算法等，它們所考慮的效用函數都為單一類型。而文獻[6-7]雖然針對不同電器的使用情況和耗能類型，將電器分為彈性、半彈性和非彈性，仍然沒有考慮電器分類所帶來的不同類型的效用函數。文獻[8-12]考慮了在實時動態價格算法中，由于可再生資源和傳輸損耗對住宅需求響應的不確定性，研究了如何鑒別、剔除不穩定供電商和惡意用戶，但是，并沒有考慮電力市場實時電價隨效用函數的變化。另外，一些文獻還研究了多目標的實時電價優化模型，考慮含風力和時間等多重約束耦合的實時電價及價格預測模型，利用當市場供需平衡時才能實現出清價格的原理，得到了實時電價的更新算法[13-15]。

在利用最優化方法解決實時電價問題中，大多數的研究都是基于效用函數最大化、成本函數最小化建立的。考慮單一類型效用函數的社會福利最大化模型，由于效用函數是凹函數，對應的優化問題為凸優化，利用Lagrange 對偶分解法、牛頓法、梯度投影法等方法求解，得到Lagrange乘子，即實時電價的影子價格[3,16]。但是，在現代網絡時代，邊際效益在有些情況下是增加的，如中國移動通訊，隨著用戶的增多，邊際效益是增加的，也就是說，效用函數是非凹函數。類似的，本文考慮多類用戶多類效用函數并存的社會福利最大化模型，該模型不再是凸優化問題，不能按照現有的方法解決。文獻[17]中提出了邊際效用非遞減用戶的實時電價方法，利用增廣Lagrange 乘子法得到了影子價格的存在唯一性。文獻[18]考慮了電器分類下不同類型的效用函數，文獻[19-20]利用Karush-Kuhn-Tucher（KKT）系統解決該類實時電價問題，并得到了較好的效果。

本文考慮同時含有凹效用函數和非凹效用函數兩種情形并存的社會福利最大化模型，根據微觀經濟學中出清價格滿足市場供需平衡原理，通過求解KKT 最優性條件，證明了Lagrange 乘子的存在唯一性，進一步得到了一種基于KKT 系統的分布式實時電價更新算法。在求解過程中，供電側的最優產電量與用電側的最優用電量可以分別計算得到，這樣也保護了用戶的隱私。最后將數值仿真結果與固定電價算法下的社會福利相比較，證實了該算法的合理性、有效性。

2 系統模型

2.1 效用函數

效用函數是微觀經濟學中的概念，通常用來表示消費者在消費中所獲得的效用與所消費的商品組合之間數量關系的函數，以衡量消費者從消費既定的商品組合中所獲得滿足的程度。效用函數有多種形式，這里按照用戶不同，分兩種情形討論。

對于一般用戶來說，隨著電力消費越來越高，用戶的滿意度隨之增長，但是，到一定程度會達到飽和，適合采用凹效用函數，即(x,ω)≤0。如對數函數、分片線性函數、二次函數等，本文采用如下二次函數[17]：

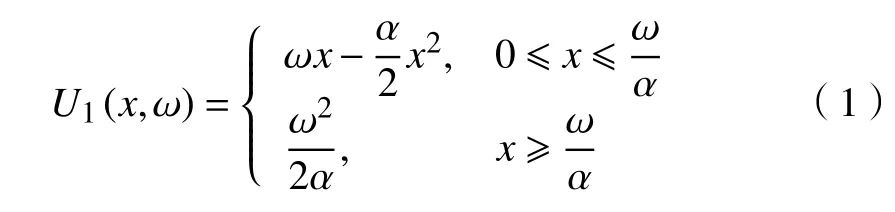
式中：x代表用戶的用電量，不同用戶不同時間段彼此獨立；α為預先給定的參數，α ≥0；ω代表用戶滿意度參數，隨著時間、溫度等變化，各個用戶之間也各不相同。

對于一些大工業、商業用戶，由于電力消費滿意度不同，效用隨著產值的改變而變化很大，在一定的電力消費階段，效用函數值的增加速度會隨著電力消費水平迅速增加，如果仍采用凹效用函數，不再貼近實際生產狀況。根據微觀經濟學原理，選取適當的非凹效用函數更加貼切。如S 型函數，即Sigmoid 函數[21]：

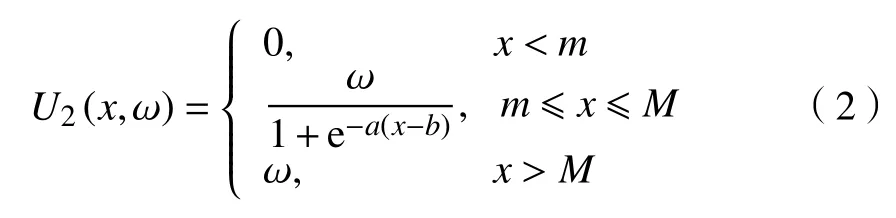
式中，a，b為預先給定的參數。

Sigmoid 函數是單調連續增函數，表示一些大用戶在用電量過低或過高時效用變化緩慢，在用電量適宜的階段，效用變化迅速。注意到參數b為函數的拐點，即

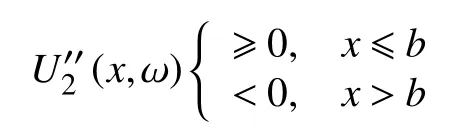
2.2 成本函數

假設供電商每次發電成本與產生的能量數量是單獨相關的，可由成本函數來表示。通常成本函數是一個單調增加的嚴格凸函數，目前普遍采用的成本函數為二次函數，即

式中：ak，bk，ck為預先給定的參數，ak＞0，bk,ck≥0，隨著時段不同而變化；Lk為時段k內的產電量。

2.3 優化問題

假設在某個區域電力系統中有一個供電商、多個用戶。N為所有用戶集合，每個用戶i∈N,，其中，Nc代表采用凹效用函數的用戶集合，Ninc代表采用非凹效用函數的用戶集合。實時電價理論上指某一時刻的費用，為了方便起見，將一個時間周期（如一天24 h）分為k個時段（如24 個時段），記K={1,2,···,k}為所有時段的集合。符號表示消費者在第 個時段的用電量，滿足，其中，表示用戶i在第k個時段最小用電量，即不斷電的情況下滿足基本的生活要求，表示用戶i在第k個時段所有電器充分利用的最大用電量。符號Lk表示第k個時段供電商的產電量，它滿足表示第k個時段內最小和最大產電量，要求能夠提供在第k個時段所有用戶的最小用電量，保障基本生活要求，即

在整個電力市場中，從社會福利最大化角度考慮，基于兩個目的：最大化所有用戶的效用之和，同時最小化供電側的成本，從而建立如下模型：

式（4）中目標函數為社會總福利，第一個約束條件含義為在每一時段，電力市場不斷電的情況下，所有用戶側的用電總量不會超過供電側的產電量。

3 模型求解

3.1 模型分析與Lagrange 乘子的性質

在電力市場的消費過程中，每個時段的電力消耗可以看成是完全獨立的，用戶彼此之間也是獨立的，這樣整個社會福利最大化問題就可以轉化為只需考慮某一個時段的社會福利最大化問題，整個社會福利最大化模型可以被分為k個子問題：

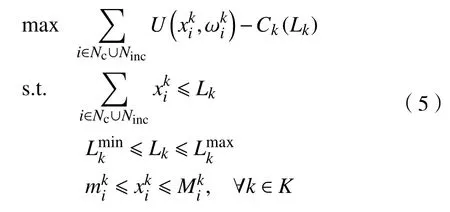
求解問題（5）有多種方法，如集中式內點法、梯度投影法[3]、牛頓法[19]等。事實上，優化問題的Lagrange 乘子，在電力市場實際問題中代表電價的影子價格，它反映了社會資源配置達到最優的一種價格，用來指導供電商調整電價。因此，可以通過求解優化問題（5）的KKT 條件，尋求Lagrange 乘子，即影子價格。定理1 首先給出優化問題（5）的Lagrange 乘子是存在且唯一的。

定理1[17]假設優化問題（5）中效用函數是連續可微的，由式（1）和式（2）給出，成本函數Ck(Lk)由式（3）給出，則優化問題（5）在最優點的Lagrange 乘子存在且唯一。

定理1 說明優化問題（5）的Lagrange 乘子存在且唯一，由于優化問題的約束條件都是線性的，滿足線性獨立約束規格[22-23]，從而滿足KKT 條件，這樣就可以通過求解KKT 系統來進一步求解Lagrange 乘子，即實時電價的影子價格。

3.2 分布式算法

考慮社會福利最大化問題（5）對應的KKT 系統：

其中，第一個約束的Lagrange 乘子 λk代表了實時電價的影子價格，用于指導供電商調整電價。產電量約束條件的Lagrange 乘子為，用電量約束條件的Lagrange 乘子為。

用戶側和供電側的邊際效用和邊際成本為

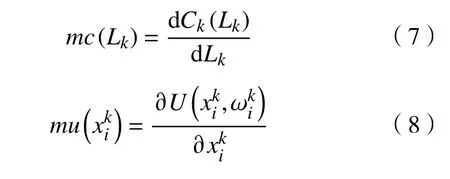
根據微觀經濟學原理，當電力水平目前沒有達到飽和的情況下，市場供電量與需求量達到平衡時，市場價格為出清價格[21]，從而建立實時電價迭代更新公式為

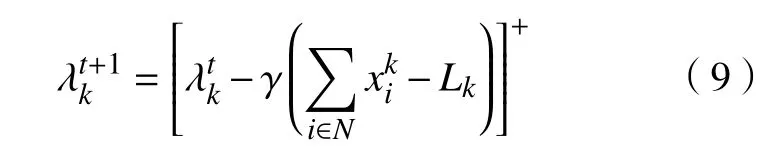
由式（9）可知，當電力市場的供電量和需求量保持一致時，即供需平衡時，算法收斂，此時為影子價格的最優解，指導供電商調整電價，得到市場出清價格。

定理2實時電價迭代式（9）中每個用戶的用電量和產電量Lk可以分別由下列公式：

給出。

證明a.當產電量或者用電量達不到最大或最小值時，由式（6c）可知，產電量約束條件的Lagrange 乘子取值為0，將式（7）代入式（6a）可得，此時產電量為，這里代表邊際成本函數mc(Lk)的反函數；

進一步整理，對于供電側的產電量可以由式（10）給出。同樣分析需求側的用電量、邊際效用與影子價格的關系，可以得到需求側的用電量可以由式（11）給出。

給定某一時段k的第t次迭代的電價，利用式（10）計算出供電側的產電量，利用式（11）計算用戶側的用電量，代入式（9），更新實時電價。這樣，供電側的產電量和用電側的用電量就可以分開計算，保護了用戶的隱私。

根據以上討論，現給出實時電價更新算法。

算法1（用戶側）：

步驟1當k∈K時，對所有用戶i∈N，初始化

步驟2若t∈T，從供電商處接收電價；

步驟3利用式（11）更新用電量；

步驟4將用電量的信息傳遞給供電商。

算法2（供電側）：

步驟1當k∈K時，初始化

步驟2若t∈T，

b.利用式（10）更新產電量Lk；

步驟3若停止準則成立，則算法停止；否則，重復步驟b—d。

前面利用KKT 條件的結論給出了供電側和用戶之間的用電策略，在算法中，實時電價的更新只需要知道用戶側的用電量和供電側的產電量，實現了供電側和用戶側分離，無需知道每個用戶的效用情況，保護了用戶的隱私。該算法不僅適用于采用凹效用函數的用戶，同樣也適用于部分采用非凹效用函數的大工業、商業用戶。

4 數值仿真

4.1 參數設置

假設所考慮的電力系統有1 個供電商、10 個用戶，其中，8 個用戶采用二次效用函數，2 個用戶采用Sigmoid 效用函數。一天時間分為24 個時段。這里，成本函數參數取值ak=0.01，bk=0，ck=0。效用函數U1中取參數α=0.3，效用函數U2中取參數a=2，b=15，ω∈[1,4]隨機選取，一旦取定，在一個小周期內固定，初始電價λ0=0.56，終止參數ε=0.01。

將仿真結果與固定電價下的社會福利進行了比較，在固定電價算法中，效用函數的參數取所有用戶參數的最大值，即ωmax=4，固定電價利用公式[3]λk=ωmax-Lkα/N計算得到。

4.2 結果分析

圖1 給出了分布式算法下每個時段實時電價的變化情況，圖2 給出了實時電價下供電側的產電量和用電側的總用電量的變化情況，說明了當市場產電量與總用電量達到平衡時，實時電價得到最優值，即市場出清價格。

從圖3 可以看出，在某一時間段供電側的產電量、用電側的總用電量、實時電價在迭代14 次以后，都達到了收斂，說明了分布式算法的有效性。

圖1 一天實時電價Fig.1 Electricity real-time price of a day

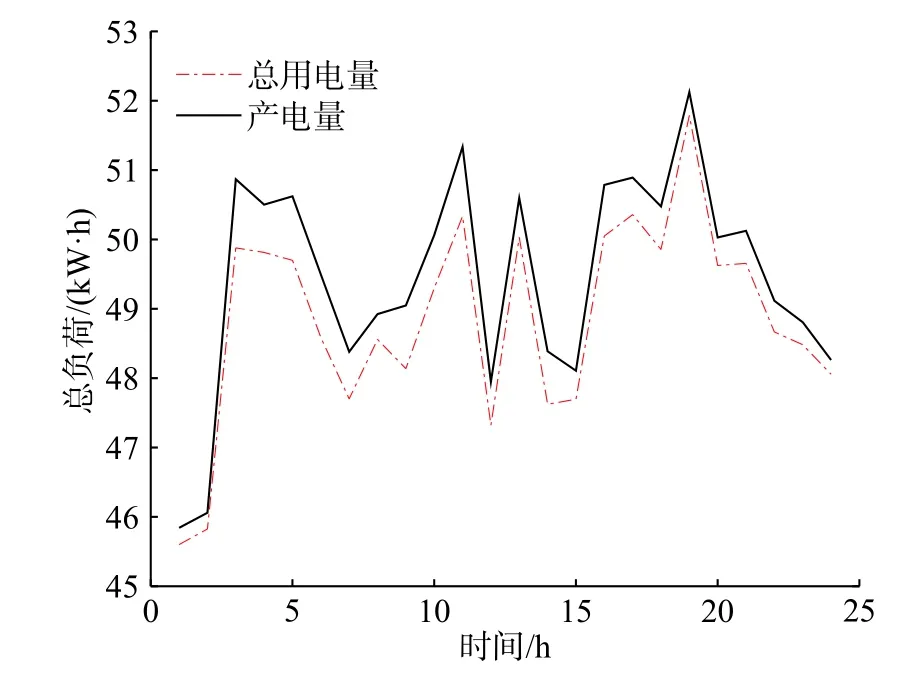
圖2 每時段產電量與總用電量Fig.2 Electricity production and consumption of a day

圖3 某時段總用電量、產電量和實時電價的迭代次數Fig.3 Electricity consumption and production and the iteration times for the real-time electricity price in a certain time period

圖4 比較了分布式實時電價算法和固定電價算法下的社會福利最大值，可以看出，每個時段實時電價下的社會福利值都大于固定電價下的社會福利最大值，說明實時電價的優越性。

考慮某一個用戶的福利，用其效用減去所付費用來表示：

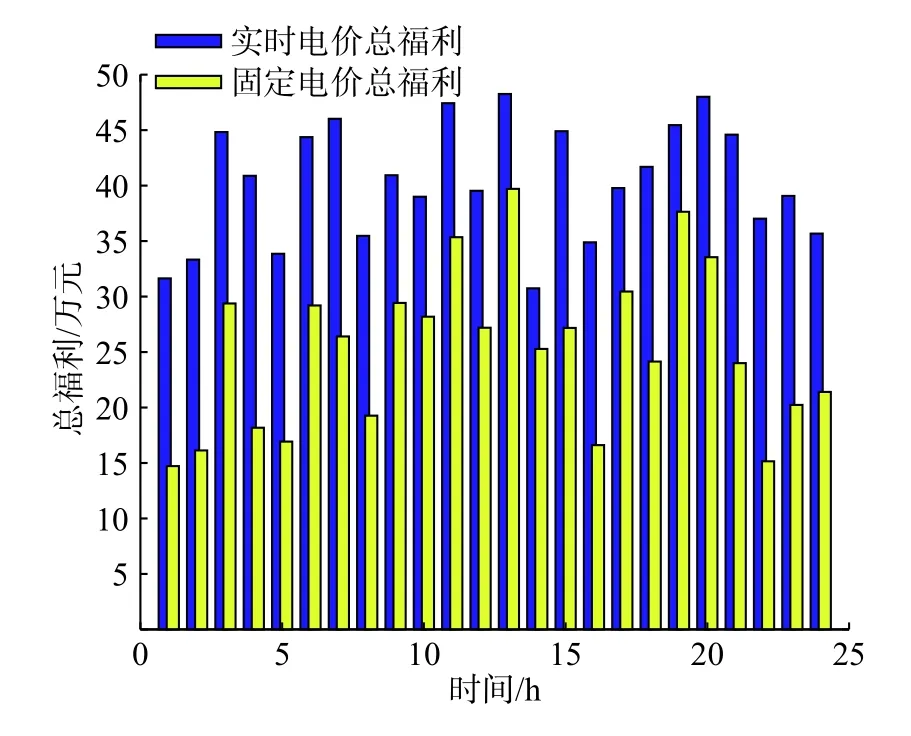
圖4 實時電價與固定電價下的社會福利值Fig.4 Social welfare value under real-time price and fixed price

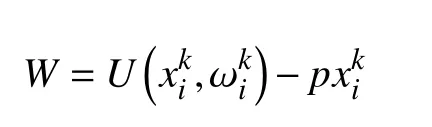
式中，p為實時電價。

圖5 以用戶3 為例，說明了在每個時段實時電價算法下的個體用戶福利都要高于在固定電價算法下的福利。

圖6 和圖7 是考慮10 個用戶分別采用不同效用函數進行比較，其中，前8 個用戶采用的是二次凹效用函數，9，10 用戶采用的是Sigmoid 非凹效用函數。在某一個時段中，雖然實時電價下的效用都大于固定電價下的效用，但是，從圖6 中可以看出，采用Sigmoid 非凹效用函數的用戶9 雖然用電量不為0，但是，圖7 中的效用卻接近于0，其他時段也有類似情形，這說明僅僅考慮耗電量比例公平對于這些用戶是不公平的，這也是作者下一步將要解決的問題。

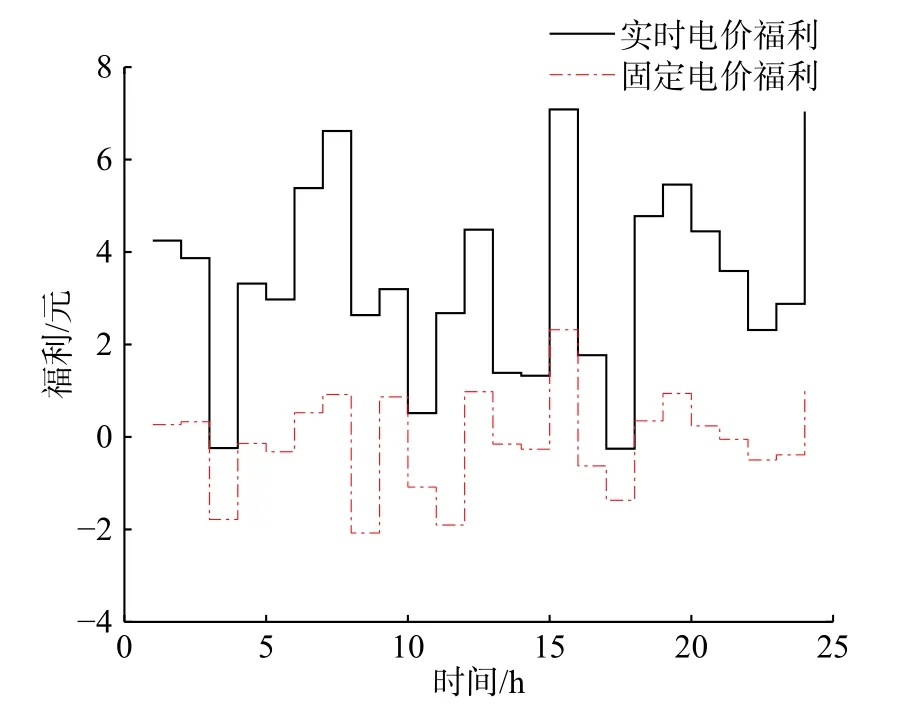
圖5 兩種電價下用戶3 的福利Fig.5 Social welfare of the user 3 under two price mechanisms

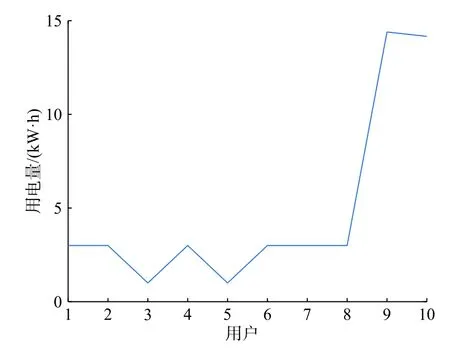
圖6 時段8 實時電價下所有用戶用電量Fig.6 All users' electricity consumption under the real-time electricity pricing in eighth time period

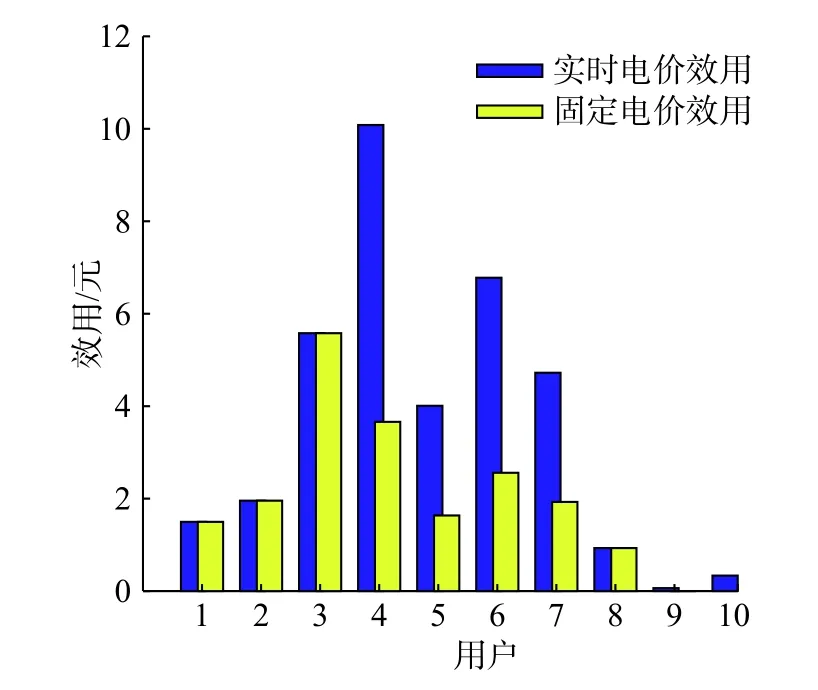
圖7 時段8 兩種電價下所有用戶的效用Fig.7 Utility of all users under two price mechanisms in eighth time period

5 結束語

針對智能電網系統具有不同類型效用函數的用戶，建立了采用凹效用函數和Sigmoid 非凹效用函數兩類用戶的社會福利最大化模型，研究了實時電價問題。在已有研究對用戶僅考慮單一類型效用函數或分類后不同效用函數基礎上，重新考慮分類為凹效用和非凹效用函數進行研究。由于所研究的社會福利最大化模型是非凸優化問題，是NP 難的，本文根據市場出清價格原理，通過研究該模型的KKT 最優性條件，得到了實時電價影子價格的迭代方法。整個算法只需知道用戶的用電量和供電商的產電量，實現了供電側和用電側的分離，既得到了分布式實時電價更新算法，又保護了用戶的隱私。仿真結果證實了算法的有效性。結果顯示，對于非凹效用函數的用戶僅考慮需求比例存在不公平的現象，這也明確了下一步研究的方向。