五圓柱體結構群繞流特性及互擾效應研究

涂佳黃，張志豪，曹 波, 3，肖毅凡，梁經群

(1. 湘潭大學 土木工程與力學學院，湖南 湘潭 411105; 2. 巖土力學與工程安全湖南省重點實驗室，湖南 湘潭 411105; 3. 中車株洲電力機車有限公司，湖南 株洲 412000)

自然界與工程界中，柱體結構大多以結構群的形式出現，如高層建筑群、冷卻塔群、海洋平臺立柱和海洋立管等。隨著柱體結構數目與排列方式的改變，多柱體結構群布置形式更加多樣化，從而導致其繞流問題也變得更加復雜。

現階段，一些學者對圓柱體結構群繞流問題開展了一系列的物理試驗和數值計算研究，主要集中于三/四圓柱體群工況[1-8]。Lam和Zou[1-2]題組運用數值模擬與試驗方法對三/四圓柱體群繞流問題進行了研究，分析了布置方式、間距比與雷諾數等參數對圓柱體群的流體力系數和流場流動模式的影響。同時，將數值結果與物理試驗結果進行了對比驗證，發現兩者吻合較好，驗證了數值方法的正確性與可靠性。另外，顧志福和孫天風[3]與Bao等[4]分別采用風洞試驗與有限元方法對層流范圍內等邊排列三圓柱體群繞流問題進行了研究，并分析了來流攻角與間距比參數對圓柱體的流體力系數和流場分布特性的影響。最近，Gao等[5]與Tong等[6]對低雷諾數范圍內方形排列四圓柱體繞流問題進行了數值模擬，分析了雷諾數對圓柱體群泄渦模式的影響并將其進行了歸納分類。Zou等[7]運用有限體積法研究低雷諾數下間距比對菱形排布四圓柱體群三維繞流特性影響，并與水槽試驗結果對比分析驗證其數值方法的正確性，研究發現狹窄間隙流模式到渦流沖擊模式的轉變發生在間距比為3.0工況。Wang等[8]對Re=8 000時正方形排列四圓柱體群繞流問題進行了物理試驗研究，分析了來流攻角和間距比對四圓柱體繞流特性及其互擾效應的影響。

近幾年，國內外學者們對陣列式排布柱體群繞流問題開展了一些研究工作[9-13]。Nicolle和Eames[9]采用高精度計算方法對亞臨界雷諾數下Re=2 100不同數量單圓柱體組成的固定直徑比的陣列圓柱體群繞流問題進行了二維數值計算，分析了空隙流對陣列圓柱體群繞流特性的影響，并觀察到三種典型的流場模態。李強[10]對九圓柱體組合結構群繞流特性問題進行了水槽試驗和數值計算，發現圓柱體群直徑與單個圓柱體直徑比和雷諾數對圓柱體群尾流形態影響顯著。Ma等[11]對正方形排列九圓柱體繞流問題進行了試驗研究，分析間距比和雷諾數對圓柱體的流體力系數及其尾流場特性的影響。與雷諾數相比，尾流場特性和流體力對間距比參數的變化更為敏感。

綜上，現階段對多柱體結構群繞流特性及互擾機理的認識還未成熟。文中對“X”形排列形式的五圓柱體在亞臨界雷諾數下三維繞流問題進行了數值計算，主要分析來流攻角和間距比對五圓柱體結構群三維繞流特性的影響，并揭示“X”形排列五圓柱體結構群的互擾效應及其內在機理。

1 數值計算理論

1.1 流體控制方程

基于大渦模擬湍流模型，通過濾波函數將大尺度渦和小尺度渦分離，大尺度渦用N-S方程直接求解，小尺度渦通過亞格子尺度模型建立與大尺度渦的關系并進行模擬。濾波函數為：

(1)

(2)

式中：Δ為計算網格體積，G(x,x′)濾波函數。經濾波分析后，不可壓縮流體的Navier-Stokes方程為；

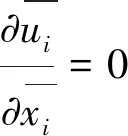
(3)

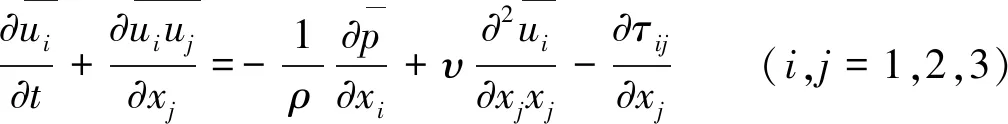
(4)

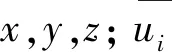
采用有限體積法對控制方程進行離散，并采用SIMPLE算法對壓力與速度耦合，空間離散壓力項和動量項分別為二階格式和邊界中心差分格式，瞬態方程為邊界二階隱式格式。

1.2 無量綱參數

文中相關參數計算式如下：阻力系數CD=2FD/(ρU2HD)，升力系數CL=2FL/(ρU2HD)，壓力系數CP=2(P-P∞)/(ρU2)，斯特勞哈爾數Sr=fsD/U。其中，FD與FL分別為阻力與升力；H和D分別為柱體軸向高度和直徑，P為靜止壓力，P∞為無窮遠處壓力且P∞=0，fs為漩渦脫落的頻率。

2 計算模型和網格劃分

計算域的邊界條件設置：速度入口邊界，即ux=U=1.0 m/s，uy=uz=0；壓力出口邊界，即p=0；上下壁面和前后壁面邊界為對稱邊界條件；圓柱壁面邊界為無滑移壁面條件，即ux=uy=0。

文中的計算流域采用結構化六面體網格來劃分，網格總數約6.2×106，柱體徑向長度上的節點數為42，采用圓柱為中心范圍內的十字型加密區間采用Otype型，加密區域為5D×5D，加密層數為8層。對靠近圓柱體壁面的網格進行局部加密，這樣可以更好地刻畫邊界層處的流場。同時圓柱體后方的尾流區域也進行局部加密處理，如圖2所示。另外，從圖2可知網格加密區未產生網格畸變。

圖1 計算模型與來流攻角示意Fig. 1 Schematic diagram of the computational model and incident angle

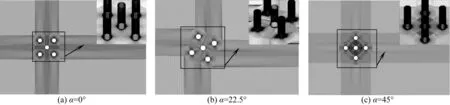
圖2 網格劃分示意Fig. 2 Schematic diagram of the mesh in different cases

3 計算參數選取及驗證

3.1 計算參數分析

本節以L/D=4.0工況下正方形排列四圓柱體結構群(α=0°)作為研究對象進行計算參數研究，分析時間步長、圓周節點數和壁面網格尺度對四圓柱體的阻力系數平均值和斯特勞哈爾數的影響，并引入文獻[12]的結果進行對比。文中時間步長符合克朗數(Cr，且取Cr=1)計算公式要求：Δt=(Cr) Δx/U，通過計算可知時間步長取0.01可滿足要求。通過對比發現，當Δt較大時會導致計算結果發生偏差，而較小的Δt會消耗較大的計算資源，其中平均阻力系數最大誤差約為3%，Sr最大誤差約為7%，詳細見表1。綜合計算資源的消耗、頻域采樣率和計算結果有效性，本算例的網格與時間步長均選用Case4方案。同時邊界層第一層高度均滿足y+≤1.0的條件。本文結果與文獻[12]結果存在一定細小差異，這主要是由于文獻[12]采用了二維模型對問題進行求解，其次可能是兩者選取了不同的湍流模型。

表1 時間步長、圓周節點數和壁面網格尺度對正方形布置四圓柱體平均阻力系數、斯特勞哈爾數的影響(L/D=4.0)

Tab. 1 Effect of time-step, nodes of circumference and wall grid scale on mean drag coefficient and Strouhal number of square-arranged four circular cylinders (L/D=4.0)

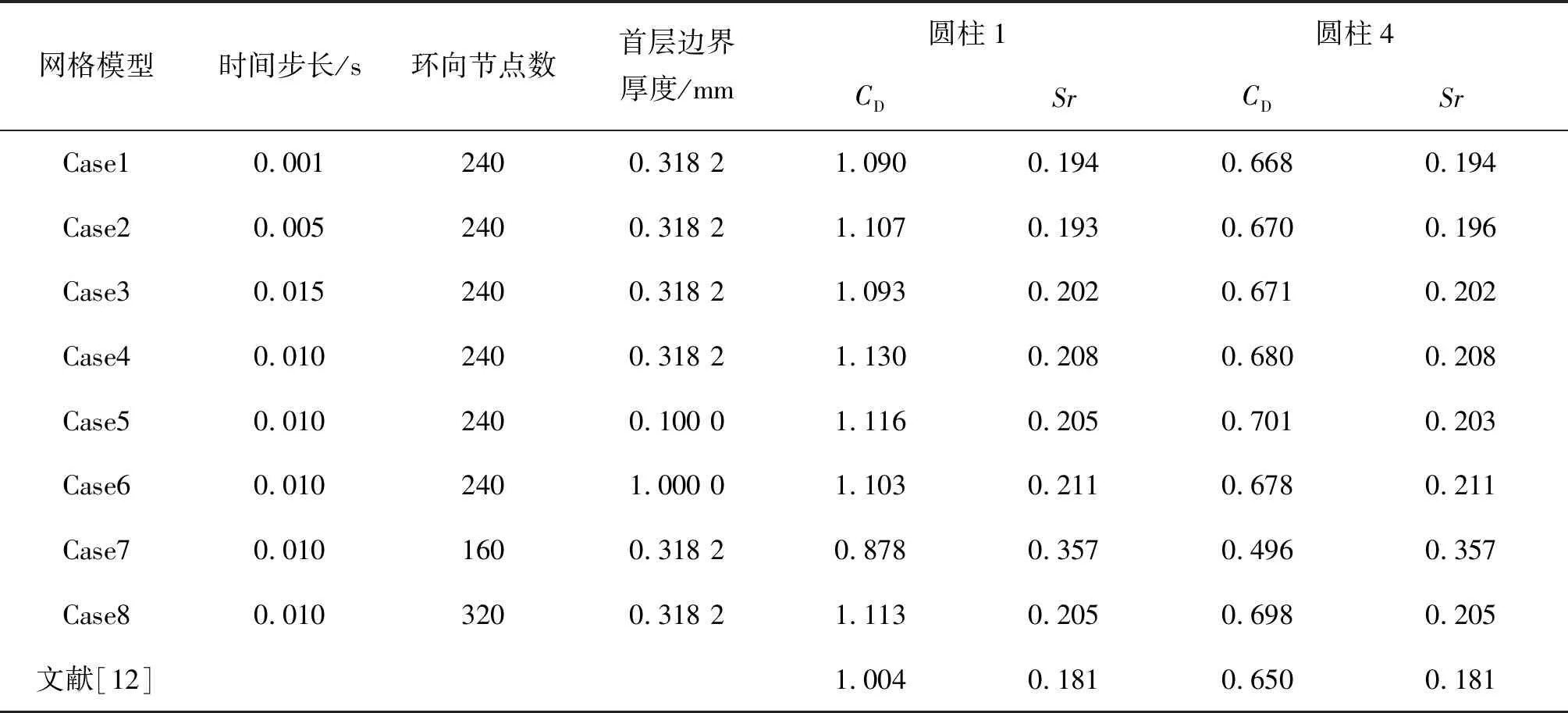
網格模型時間步長/s環向節點數首層邊界厚度/mm圓柱1圓柱4CDSrCDSrCase10.0012400.318 21.0900.1940.6680.194Case20.0052400.318 21.1070.1930.6700.196Case30.0152400.318 21.0930.2020.6710.202Case40.0102400.318 21.1300.2080.6800.208Case50.0102400.100 01.1160.2050.7010.203Case60.0102401.000 01.1030.2110.6780.211Case70.0101600.318 20.8780.3570.4960.357Case80.0103200.318 21.1130.2050.6980.205文獻[12]1.0040.1810.6500.181

一些學者們采用阻力系數平均值積分曲線(average drag coefficient intergral curve)判斷湍流流動是否達到穩定狀態[13]。基于該方法，當柱體結構的阻力系數平均值時程曲線由陡峭逐漸趨于平穩，則可認為湍流流動達到了穩定狀態，即可以開始提取足夠多的相關物理量進行數據處理與分析。為使渦脫落充分發展，文中模擬總時間為300 s，且數據采樣的時間為t>250 s即在525個渦脫落之后，共采樣了113個渦脫落周期；其中數據采集的時間間隔為0.01 s，渦脫落周期為0.47 s。

3.2 算例驗證

將單圓柱體和正方形排列四圓柱體結構群(α=0°)兩個經典算例的數值計算結果與已有文獻結果進行對比分析，結果見圖3。

圖3 單圓柱尾流區時均速度和正方形排列四圓柱體的阻力系數平均值與文獻結果對比Fig. 3 Comparisons between mean streamwise velocity, mean drag coefficients and the existing data of the cases of a single cylider and four square-arranged ones

從圖3(a)可以看出，單圓柱體的尾流區不同特征位置處的時均速度分布與相關文獻[15-16]吻合較好。從圖3(b)可以看出，正方形排列四圓柱體的阻力系數平均值隨間距比的變化趨勢與文獻[8, 12]記載的內容基本一致。從而驗證了這里選取的計算模型、計算方法和相關參數設置的準確性和可靠性。為方便描述圓柱體之間的相對位置關系，特此將五個圓柱體分別命名為C1～C5。

4 計算結果與分析

在流攻角為0°、22.5°和45°工況下，主要對L/D=2.0、3.5、5.0和7.0四種間距比工況下，五圓柱體結構群繞流問題進行數值研究，分析了五圓柱體的三維渦結構、圓周平均壓力及流體力系數隨來流攻角和間距比的變化規律，并解釋其互擾效應和流動控制機理。

4.1 流場特性分析

結構表面剪切層的發展與相互作用及尾渦結構的分布會影響流場分布特性，導致柱體表面所受的壓力分布發生變化，進一步改變圓柱體表面受到的流體力。圖4給出了L/D=2.0、3.5、5.0和7.0四種間距比工況下及不同來流攻角下的五圓柱體結構群瞬時渦量圖。

圖4 不同工況下五圓柱結構群瞬時渦量Fig. 4 Three-dimensional vorticity of five circular cylinders in different cases

當間距比較小時，由于間隙區域過于狹窄，圓柱體群的剪切層相互干擾耦合，五圓柱體結構群之間的互擾作用以臨近效應為主，并且可觀察到波狀剪切層(corrugated shear layer，簡稱CSL)和尾渦第一次卷起位置FRU (the first roll up)[14]。如圖4所示。在中間圓柱(C5)的阻擋作用與間隙流的高速流動共同影響下，上游兩圓柱體(C1和C2)的上下表面剪切層分別斜向下和斜向上卷起CSL并形成回流區。同時，間隙流沖擊C5后形成穩定的回流區，沿圓周向周圍流動并沖擊下游兩圓柱體(C3和C4)，使得下游兩圓柱體的剪切層在尾流區較遠處卷起產生較大且單一的寬尾流渦街，如圖4(a)和圖4(b)所示。另外，C3、C4和C5處于背流面被屏蔽狀態且其上下表面剪切層均未發生擺動現象。這種流動模式與文獻[12]所記載的類似，稱之為穩定屏蔽模式。

隨間距比的增大，上游兩圓柱體上下表面剪切層斜向卷起偏離角度逐漸減小，其尾流渦街發展越來越充分，撞擊下游圓柱體并改變下游圓柱體的渦脫落模式，并更容易觀察到CSL和FRU。下游兩圓柱體受到間隙流的沖擊作用及其他圓柱體尾流結構的干擾作用逐漸減弱，如圖4(d)和圖4(g)所示。當α=22.5°時，均勻來流斜向流經狹窄間隙區域使得C3完全處于背流面被屏蔽，從而會影響其順流向阻力系數的大小。需要注意的是，C1和C2上下兩側流體流動特性幾乎一致，而其他圓柱體流體繞流特性均存在較大差異性。該流動現象會導致五圓柱體所受的流體力發生變化。當α=45.0°時，隨間距比逐步增大，兩側圓柱體(C2和C4)尾流渦街的發展受其他圓柱體的影響逐漸減小且其渦脫落模式趨于穩定。當L/D=3.5時，C1和C5的剪切層向下游延展的位移逐步增大，五圓柱體結構群之間的互擾效應以臨近效應和剪切層干擾為主，如圖4(f)所示。當L/D=5.0時，中游圓柱體C5尾流區會發生漩渦脫落現象。然而，C1剪切層仍會再附著在C5表面并影響其漩渦的形成和脫落，五圓柱體結構群之間的互擾效應由剪切層干擾和尾渦沖擊共同作用，如圖4(i)所示。

當間距比大于臨界值時，上游兩圓柱體尾渦結構的發展幾乎不再受中間圓柱體及下游兩圓柱體的干擾，其繞流特性接近于單圓柱體工況；中間與下游兩圓柱體的尾流分布特性會逐漸趨于穩定。另一方面，除受到上游圓柱體尾流撞擊作用外，下游兩圓柱體還會受到間隙流的沖擊作用，如圖4(j)所示。當L/D=7.0，α=22.5°時，五圓柱體結構群之間的互擾作用以偏斜尾流沖擊干擾為主。上游圓柱體的渦脫落并非直接撞擊下游圓柱體，而會改變下游圓柱體兩側或一側的流體流動特性，導致C3和C5上下表面所受的橫流向流體力不一致，如圖4(k)所示。另外，當α=45.0°時，C1和C5尾流區均產生周期性卡門渦街，五圓柱體結構群之間的互擾效應轉變至尾流效應，如圖4(l)所示。

4.2 柱體表面壓力分布特性分析

圖5 當來流攻角0.0°時，z/H=0.5截面處五圓柱體群時均壓力系數分布特性隨間距比的變化Fig. 5 Mean pressure coefficient distributions along the circumference of five cylinders versus L/D at α=0.0° and z/H=0.5

值得注意的是，L/D=2.0工況下，C3與C4的壓力分布存在顯著的差異性。這主要與柱體周圍流場分布特性有關，如圖6(a)所示。一方面是上游柱體尾流與間隙流對迎流面的沖擊作用不同，另一方面是柱體結構附近尾流區漩渦形態及其影響的變化。

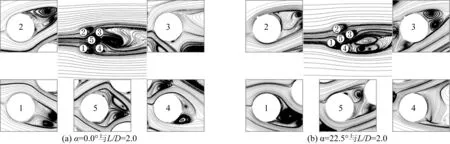
圖6 L/D=2.0時，α=0.0°與22.5°工況下z/H=0.5截面處五圓柱體群時均流線Fig. 6 The time-averaged streamline with z/H=0.5 axial height at α=0.0° and α=22.5° with L/D=2.0

當α=22.5°時，圓柱體群之間的位置呈錯列形式，內在的互擾效應更為復雜，導致柱體結構表面的壓力分布特性會發生顯著變化，如圖7所示。間距比的變化對C1的駐點位置及其平均壓力系數的影響較小，對其最小平均壓力系數位置及相應數值影響較大，如圖7(a)所示。特別在小間距比工況下，C2與C3的最小平均壓力系數分別達到了-2.17和-1.98。同時，C3下表面沒有出現正壓區。這是因為柱體群間的相互作用，導致產生了間隙流高速流動現象，使得尾流區渦結構呈偏斜狀，如圖6(b)所示。

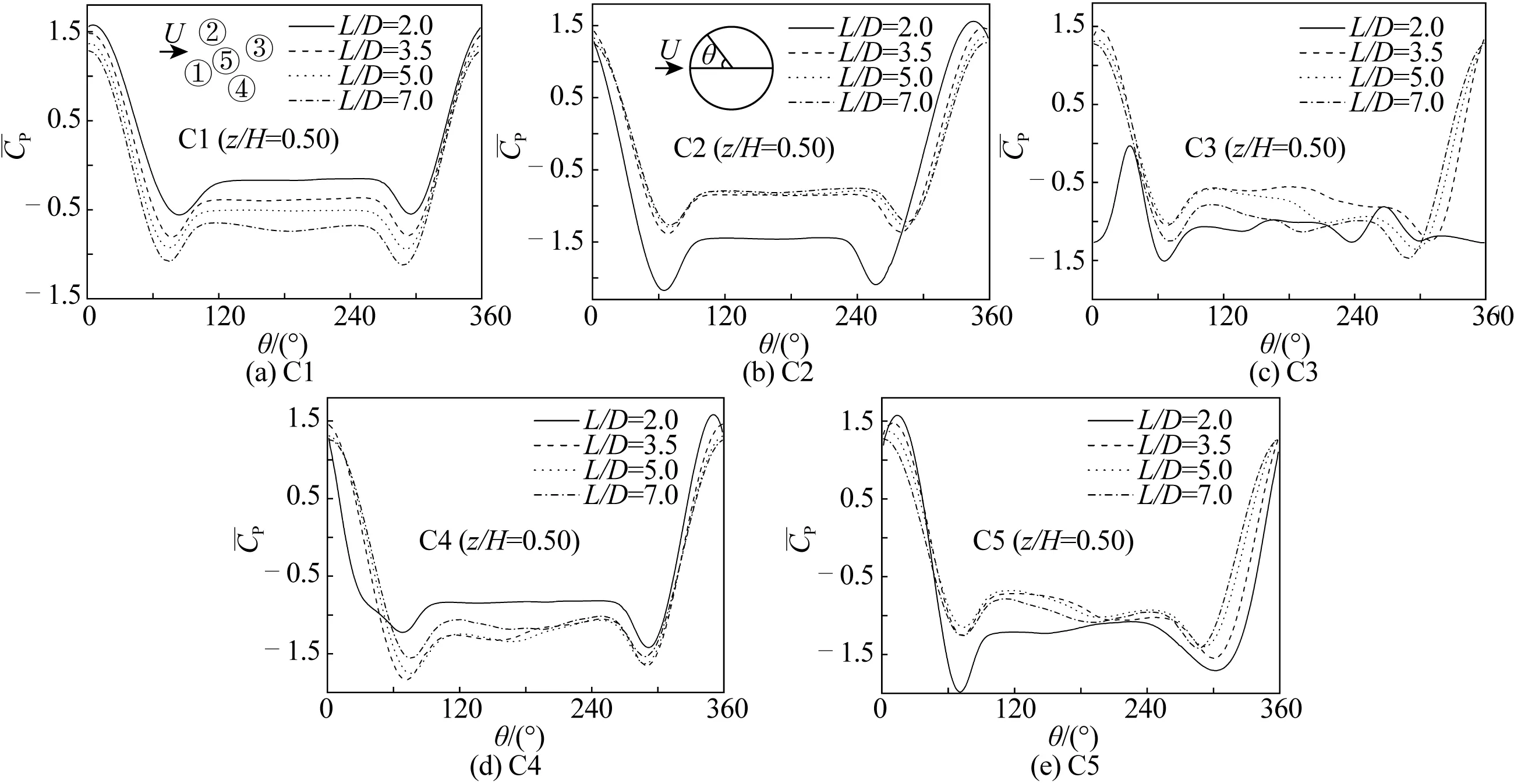
圖7 當來流攻角22.5°時，z/H=0.5截面處五圓柱體群時均壓力系數分布特性隨間距比的變化Fig. 7 Mean pressure coefficient distributions along the circumference of five cylinders versus L/D at α=22.5° and z/H=0.5

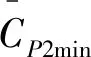
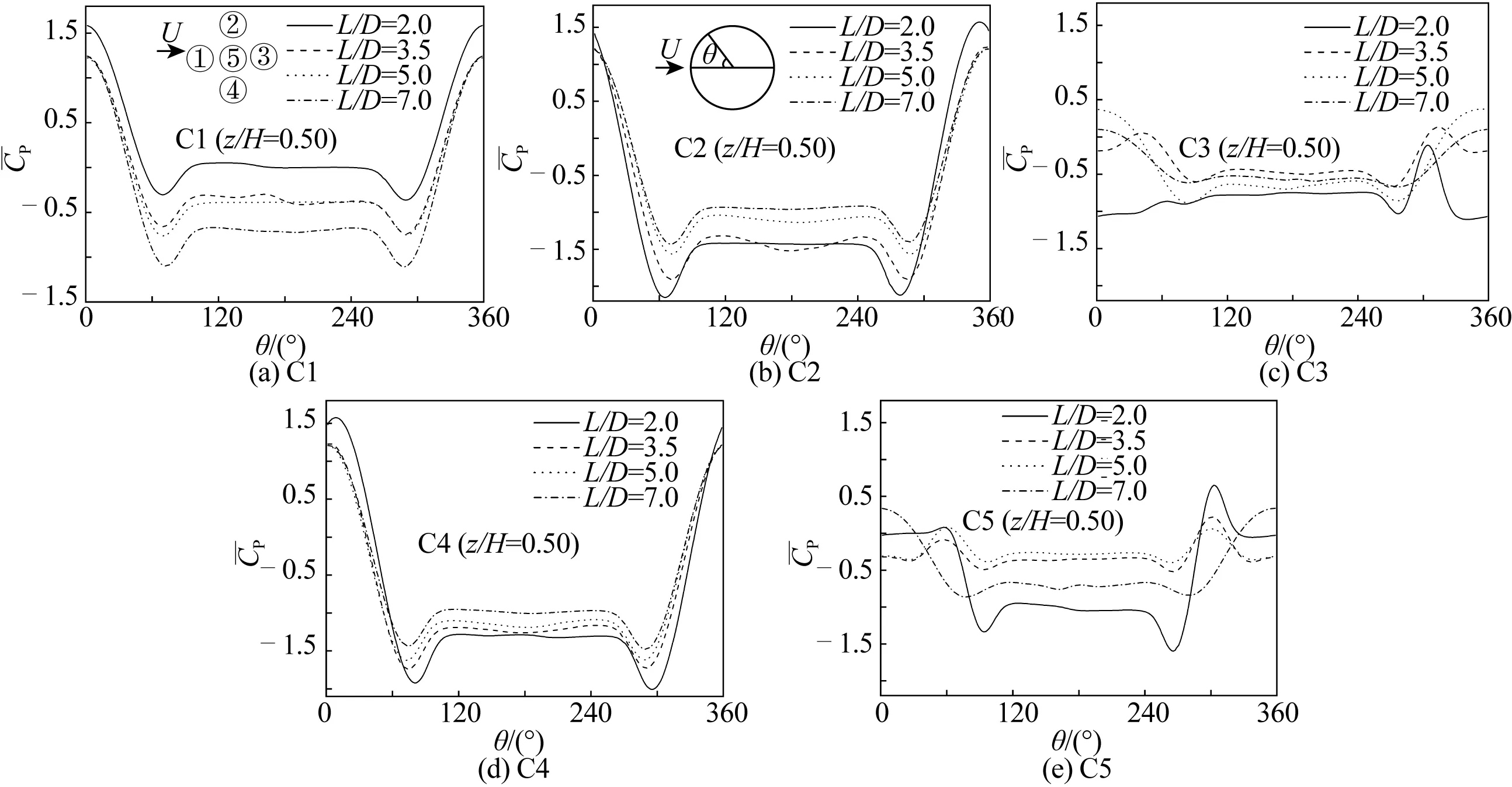
圖8 當來流攻角45.0°時，z/H=0.5截面處五圓柱體群時均壓力系數分布特性隨間距比的變化Fig. 8 Mean pressure coefficient distributions along the circumference of five cylinders versus L/D at α=45.0° and z/H=0.5

4.3 流體力系數特性分析

本節分析了α=0°、22.5°和45°工況下，五圓柱體的阻力系數和升力系數平均值及其均方根值隨來流攻角和間距比的變化規律，并與單圓柱工況的結果進行了對比分析，見圖9～圖11所示。

當來流攻角α=0°時，該五圓柱體結構群布置形式使得上下兩排并列布置雙圓柱體關于y=0的中心面對稱，導致上游兩圓柱體(C1和C2)的流體力系數統計值幾乎一致，同時，下游兩圓柱體(C3和C4)也會呈現相同的趨勢，見圖9(a)。值得注意的是，當L/D≥5.0時，五圓柱體的尾流均已發展充分，如圖4(g)和圖4(j)所示，誘發其阻力系數平均值保持穩定。

圖9 來流攻角0°工況，五圓柱體流體力系數隨間距比的變化Fig. 9 Variation of fluid force coefficients of five circular cylinders versus L/D at α=0°

由圖9(b)可知，上游兩圓柱體的升力系數平均值大小幾乎相同但符號相反，下游兩圓柱體的升力系數平均值亦是如此，這種情況反映了上排兩圓柱體與下排兩圓柱體之間的相互排斥作用。特別地，當L/D=2.0時，上排兩圓柱體與下排兩圓柱體的升力系數平均值絕對值較大，說明此時圓柱體之間有較強的排斥作用。

不同間距比工況下，下游兩圓柱體的升力系數均方根始終大于上游兩圓柱體，如圖9(c)所示。隨間距比的增大，除L/D=2.0工況外，上游兩圓柱體的升力系數均方根呈現單調遞增，并逐漸接近于單圓柱體工況的結果，與文獻[9]中計算結果基本一致。從圖9(c)可知，當L/D≥3.5時，下游和中間圓柱體的升力系數的脈動性較強。這是因為五圓柱體的尾渦結構相互耦合與干擾從而使得C3、C4和C5三圓柱體的升力脈動性增強。

當α=22.5°時，隨間距比逐漸變大，C3、C5與C2三者之間的干擾作用逐漸減弱，進而導致其阻力逐漸減小。同時，C3的阻力系數平均值單調增大至1.21。另一方面，當間距比較小時，由于C3的迎流面與背流面均受到一對漩渦沖擊作用，如圖6(b)所示，導致其順流向的阻力接近零。

由圖10(b)可知，因為小間距比工況下，高速間隙流的存在，使得C2和C4上下表面的流體流速有較大差別，進一步導致其上下表面存在較大壓力差。隨間距比逐步增大，C2和C4上下表面的流體流速差異逐步減小，其壓力差也逐步減小，導致升力系數平均值變為零。特別，當L/D=7.0時，C3和C5升力系數平均值仍然不為零，這是由上游圓柱體(C1和C2)渦脫落往下游傳播使得C3和C5兩側流體流動特性發生改變而引起的，如圖4(k)所示。

圖10 來流攻角22.5°工況，五圓柱體流體力系數隨間距比的變化Fig. 10 Variation of fluid force coefficients of five circular cylinders versus L/D at α=22.5°

當L/D≥3.5時，C3、C4和C5的升力系數均方根較大，這表明其尾流渦街的發展受到了C1和C2尾流的較強干擾作用，從而使得三者的升力表現出較強的脈動性，見圖10(c)。

當來流攻角α=45.0°時，小間距比工況下，除C3外，其他四圓柱體的阻力系數平均值均較大，見圖11(a)。這是因為C3完全處于尾流場而被屏蔽，其他四個圓柱體均會受到尾流的影響。當L/D=3.0時，C2和C4的阻力系數平均值達到了1.60和1.59，此現象可能是由于C2和C4尾流區渦脫落不穩定所致。

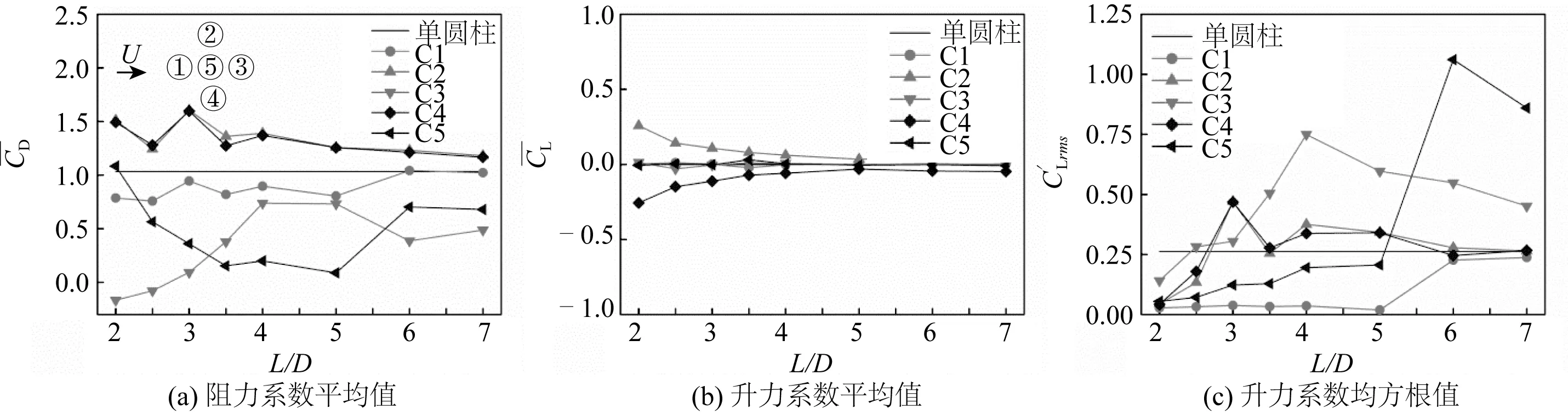
圖11 來流攻角45°工況，五圓柱體流體力系數隨間距比的變化Fig. 11 Variation of fluid force coefficients of five circular cylinders versus L/D at α=45°

同時，C2和C4的平均升力系數互為相反數且其絕對值逐漸減小，而中間排三圓柱體的平均升力系數幾乎為零，如圖11(b)所示。這是由兩側圓柱體(C2和C4)對稱布置及中間三圓柱體(C1、C3和C5)上下表面流體流動特性一致等原因引起的。

5 結 語

基于計算流體動力學方法，對亞臨界雷諾數Re=3 900時，不同來流攻角和間距比工況下，“X”形排列五圓柱體繞流問題進行了數值分析。分析來流攻角α和間距比L/D兩個參數對五圓柱體尾渦結構、壓力分布和流體力系數的影響，并進一步揭示了柱體結構群之間互擾效應。研究得出以下主要結論：

1)小間距比工況下，圓柱體群的剪切層相互干擾耦合，互擾效應十分顯著且可觀察到明顯的FRU與CSL。不同來流攻角工況下，由于柱體排列方式的改變，導致柱體群尾渦發展模式存在差異性。

2)在不同工況下，上游圓柱的時均壓力系數變化規律基本一致，僅在數值上表現出一定的差異。由于柱體間間隙流的存在，下游圓柱體平均壓力系數的對稱性規律受到干擾。

3)五圓柱體結構群流體力系數受來流攻角和間距比影響較大。隨間距比的增大，五圓柱體的平均阻力系數與脈動性升力系數發生較大變化，而升力系數平均值沿單圓柱結果曲線呈現對稱分布。