面積法推導數列{n}、{n2}、{n3}的前n項和公式①

王 彬 王 占 侯曉婷 李春蘭

(內蒙古師范大學數學科學學院 010022)

數列與函數、不等式等有著密切的聯系，又是今后學習高等數學的基礎內容之一.其中等差數列作為一種特殊的數列，是高中生探究特殊數列的開始，它對后續數列的學習無論是在內容上還是在方法上都具有積極的意義.

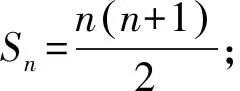
古文獻中關于等差數列的前n項和公式的推導方法，如倒序相加法、數形結合法等，也是我國高中數學教科書中慣用的方法.在我國現行6套高中數學教科書中關于等差數列的前n項和公式的推導，人教A版(2007年)、滬教版(2007年)是利用高斯的算法推導得出公式；北師大版(2010年)是先通過如何計算圓木料堆中木料的總數，引出如何計算等差數列的前n項和這個問題，再介紹高斯的算法最后推導得出公式.(6)劉紹學,錢珮玲,章建躍.普通高中課程標準實驗教科書數學5必修(A版)[M].北京:人民教育出版社,2007:48-49.人教B版(2007年)和蘇教版(2005年)先呈現某倉庫堆放的鋼管總數圖(如圖1)，再通過求鋼管總數推導出等差數列的前n項和公式；湘教版(2007年)是呈現某學校運動會開幕式的隊列站法圖(如圖2)，再通過求隊列總人數推導出等差數列的前n項和公式.

圖1

圖2

這6套教科書中關于等差數列的前n項和公式的推導，無論是通過高斯的算法進行公式推導，還是先觀察鋼管圖或者隊列圖再進行公式推導，它們本質上都是應用了加法結合律，首末兩端距離相等的每兩個數的和都等于首末兩數的和，屬于代數方法中的倒序相加法.但是只通過高斯算法來推導公式，學生僅僅是利用倒序相加法對等差數列的前n項和公式進行死記硬背；……