空軍飛機戰傷搶修隊數量預測研究
張獻逢 任柯融 黃孝禮
摘要:基于排隊論構建了搶修隊數量計算模型,以戰傷飛機排隊隊長和戰傷飛機停機時間兩個關鍵指標計算出了不同數量下飛機所需的搶救隊數量,預測了空軍飛機戰傷搶修隊的規模。
關鍵詞:搶修隊;數量;規模;排隊論
Keywords:repair teams;number;scale;queuing theory
隨著軍隊規模結構和力量調整改革的完成以及空軍三級裝備維修保障體制向兩級轉變的穩步推進[1],以中心修理廠為主體的空軍飛機戰傷搶修隊撤銷,現行的搶修隊依托修理機構設置,搶修隊的數量規模與新編制下戰區主導的作戰體系對飛機戰傷搶修任務的需求不相適應。為了滿足戰時戰傷飛機搶修需求,需要在航空兵部隊配置合理數量的搶修隊,以保證戰時飛機能夠得到有效修復。本文基于排隊論構建搶救隊數量計算模型,以預測飛機戰傷搶修隊的規模。
1 戰傷飛機搶修排隊模型
1.1 戰傷飛機搶修排隊系統的組成
根據排隊理論,將戰傷飛機搶修排隊看作是一個[M|M|C]排隊系統[2-4]。在戰傷飛機搶修排隊系統中,顧客是需要實施搶修的戰傷飛機,服務機構是實施飛機搶修的搶修隊。圖1給出了戰傷飛機等待搶修所形成的排隊系統示意圖。
戰傷飛機搶修排隊系統由輸入過程、排隊規則和服務機構三個部分組成。
1)輸入過程:指戰傷飛機到達搶修隊進入排隊系統。
2)排隊規則:戰傷飛機到達搶修排隊系統后,如果所有的搶修隊都被占用沒有空閑,此時該戰傷飛機自動加入隊列排隊等待被搶修。戰傷飛機按到達的先后順序接受搶修,即先到的飛機先被搶修。
3)服務機構:指提供搶修操作的搶修隊。
1.2 戰傷飛機搶修排隊系統的主要指標
在構建的戰傷飛機搶修排隊系統中,主要有等待搶修飛機隊長、飛機隊長、等待搶修時間和停機時間4個關鍵參數。根據排隊論系統公式,各參數的說明及表達式如下[5-9]。
1)等待搶修飛機隊長:指在戰傷飛機搶修隊列中等待搶修的戰傷飛機的數量,記為Lq。通常,Lq的值越大,表示服務系統提供服務的效率越低[10]。根據排隊論系統公式,


戰傷飛機搶修時間要求緊迫,通常為24h[11]。戰傷飛機在戰傷飛機搶修排隊系統中的停機時間是否超過24h是判斷搶修隊配置數量能否滿足作戰要求的最重要的指標。
1.3 戰傷飛機到達間隔時間及搶修間隔時間分布
在戰斗中飛機被擊傷或發生故障是一個隨機過程,可以用泊松流來描述戰傷飛機的產生規律。由于泊松分布同時滿足負指數分布,因此也可以用負指數分布來描述。戰斗中戰傷飛機的出現符合泊松分布在多個文獻中都有相應的描述。戰傷飛機的搶修時間近似服從負指數分布也在多個文獻中有所論述[2-4]。
對于戰傷飛機搶修排隊系統來說,最重要的指標就是戰傷飛機的停機時間Ws。合理地設置戰傷飛機的到達強度λ和搶修隊的平均服務率μ,可以根據排隊系統平穩的條件ρ=λ/(cμ)<1計算搶修隊c的最小值。按照飛機戰傷搶修的要求,計算不同搶修隊數量c下的戰傷飛機停機時間Ws,根據Ws是否在設置的時間范圍內,判斷c的取值是否合理。或者根據作戰任務需求確定指揮員允許的戰傷飛機停機時間Ws,選擇合適的c使Ws滿足作戰任務需求。c即為理論上需要配置的搶修隊數量。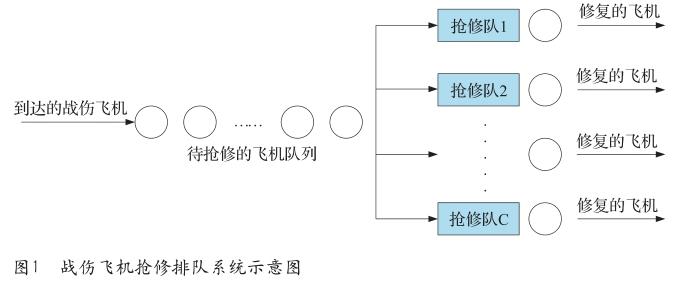
2 戰傷飛機搶修隊數量計算
2.1 戰傷飛機到達強度λ的確定
λ與參戰飛機數量、作戰天數、出動率、每天出動架次、戰傷率、戰損率、搶修水平等因素有關。因此,在計算戰傷飛機的到達強度λ時,應限定參戰飛機數量、作戰天數、出動率、每天出動架次、戰傷率、戰損率和修理水平等因素。
2.2 搶修隊的平均服務率μ的確定
根據過去的修理經驗和相關資料,并考慮到作戰飛機的不斷改進,對我軍主要的作戰機種的單機修理工時(以殲擊機為例)的參考數據進行設置,如表1所示。
假設每支搶修隊有13人,每天可工作12h,則每支搶修隊每天可提供工時為13×12=156h。每支搶修隊每天可修理156÷80=1.95架單發飛機,或可以修理156÷130=1.2架雙發飛機。
在每支搶修隊人員不變、搶修技術沒有重大突破的情況下,搶修隊對單發飛機和雙發飛機的平均服務率分別為0.1625架/h和0.1架/h,可以近似保持不變。
3 搶修隊數量配置預測
3.1 搶修隊數量配置預測模型
在某次戰斗中,某部36架飛機,每次的戰斗出動率為80.57%,空中戰損率為6%,空中戰傷率為18%,作戰天數為10天,每天出動2個批次,在良好搶修條件下,通過仿真該部隊參戰10天后能作戰、戰傷、修復和戰損的飛機隨作戰天數變化的情況如表2所示。
假設需要的搶修隊的數量為c,根據系統平穩的條件,計算得到
c>1.2
c表示搶修隊的數量,只能取整數,c=2。

上述算例按照36架飛機進行計算,在擁有2支搶修隊的情況下,戰傷飛機的停機時間為9.72h,滿足搶修時間不大于24h條件,搶修隊能夠滿足作戰搶修要求。
3.2 參戰部隊搶修隊數量配置預測
現代局部戰爭,一般實施多單位、多機種作戰。多支部隊參戰時,可以根據作戰需要,對戰傷隊集中使用,確保搶修隊發揮更大作用。在其他條件保持不變,改變參戰飛機的數量,分別以108、144、180架飛機為例計算所需搶修隊的數量。如果全部是單發飛機,需要5~8支搶修隊;如果全部是雙發飛機,需要8~12支搶修隊;如果單發飛機與雙發飛機的比例為1:1,則需要7~11支搶修隊。具體情況見表3。也可以根據單雙發飛機的實際數量,利用上述模型分別計算。
3.3 空軍搶修隊數量預測
飛機戰傷搶修隊數量規模預測,目前沒有可直接參考的模型。為此,可以按照上述計算方法對空軍搶修隊數量進行預測。預測時應遵守以下原則:一是飛機主要考慮作戰飛機,運輸機、搜救直升機等非作戰飛機和初級教練機暫不考慮。二是戰區下轄部隊,按照部隊的級別,根據機型相近原則進行預測;空軍直屬單位分別進行預測。最后將各戰區和空軍直屬單位預測的搶修隊數量累加,得到空軍所需的搶修隊數量。按照以上準則進行估算,可以預估出空軍所需的搶修隊數量。
4 結束語
隨著空軍編制體制的深入開展,部隊現有的搶修隊數量必將無法適應新體制的要求,如何配置合適數量的搶修隊,既滿足戰時作戰搶修要求,又滿足平時部隊的修理需要,是需要進行深入研究的問題。本文構建的基于一個基地飛機的所需的搶修隊計算模型,后期還需要實際戰例數據加以修正,從而得到最優搶修隊數量配置。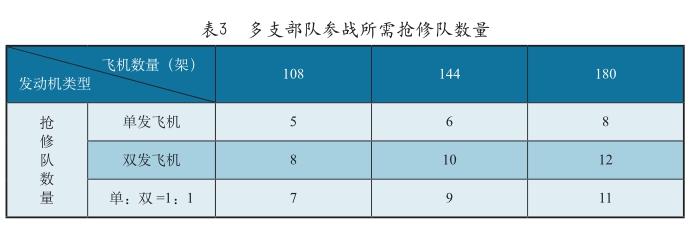
參考文獻
[1]張爽.兩級維修體制下空軍飛機戰傷搶修隊伍建設研究[J].航空兵士官,2019(3):7-8.
[2]商興華.基于排隊論的作戰飛機維修力量需求研究[J].計算機與現代化,2010(12):36-39.
[3]尹富.基于排隊論的飛機戰傷搶修需求力量配置與優化[D].信陽:空軍第一航空學院,2013.
[4]吳勇.M/M/C/m/m排隊系統模型的飛機戰傷搶修研究[J].光電與控制,2009(4):90-92.
[5]吳同晗.基于排隊論的維修保障裝備數量確定研究[J].兵器裝備工程學報,2018(11):104-108.
[6]韓震.基于排隊系統的戰時基本搶修單元指派模型[J].火力與指揮控制,2017(10):39-43.
[7]李建軍.基于排隊模型的電動汽車充電樁數量優化設計[J].數學的實踐與認知,2017(9):212-218.
[8]石磊昊.基于排隊論的油料裝備維修保障人員需求分析[J].指揮控制與仿真,2019(41):136-140.
[9]魯冬林.基于排隊論的工程裝備戰時維修力量配置[J].四川兵工學報,2013(4):60-62.
[10]陸傳賚.排隊論[M].北京:北京郵電學院出版社,1994:36-63.
[11]姚武文.飛機結構戰傷搶修[Z].信陽:航空機務士官學校,2016:3-4.
作者簡介
張獻逢,講師,碩士,研究方向:航空修理、飛機戰傷搶修新技術。

