從行為經濟學角度研究企業內員工知識共享決策
劉思涵
? 一、引言
行為經濟學結合心理學領域研究的一些結果,進而研究出了一系列模型解釋了生活中的一些經濟現象[1]。過去企業似乎更加重視企業資產的分配和投資,但是隨著人力資本理論的發展,企業越來越重視人力資本的價值,這進一步就體現在公司內部員工之間的知識共享。
? 二、企業內員工知識共享決策的環境分析
傳統經濟學領域有很多學者都對公司內員工知識共享進行了研究,例如Davenport認為在公司內有著一種關于知識的市場,在這里知識可以被買賣,買賣雙方以及市場交易原則和相應的管理者之間形成了這樣的市場[2]。所謂賣方實際上就是那些掌握著特殊專業知識和技能的從業者,而他們與買方之間達成的交易就相當于公司內部員工之間進行了知識共享。買方則是指那些需要這些特殊專業知識的組織或者個體。因為交易的這些專業知識具備壟斷和高風險的特點,故而其交易會受到市場管理者和制定的規則的調控。
西蒙接著提出賣方在知識市場進行交易時,本身可以做出兩種決策:一是選擇知識共享,二是選擇知識不共享。他們會依據一些決策準則來對這兩種決策進行評估,然后做出抉擇。一般來說他們做出決定時會依據期望效用理論,將可能獲得收益的效用值求出,然后乘以每種可能收益獲得的概率,從而求出每個決策對應的期望效用,最后在其中選擇對應期望效用最大的決策,具體分析可見表1。

表1 知識共享決策和知識不共享決策的收益表
依據表1,我們可知知識交易很是特殊。首先知識共享的成本不僅包含獲得知識所付出的努力,比如知識的價格,而且還包含因做出這種決策而造成的一些機會成本,例如不能夠在繼續壟斷這種知識、失去了專家權力等。其次共享知識所帶來的收益不僅包含金錢上的,而且還包含一些很難計量的收益,比如自我滿足感的提升、聲望的提高以及職業前景變好等。最后共享知識所獲得的收益一般都是長期的,存在著很大的不確定性。
按照Lewin提出的行為模型,我們構建了從賣方角度出發的關于知識的交易行為模型:
B=F(E,P)
在上式中,B代表賣方的交易行為,E代表其所處的市場環境,P代表其本身的一些條件。這個模型實際上也提出了個體交易行為由其所處環境和自身條件共同作用決定的。E所代表的市場環境包含了交易規定、管理者和買方。在決策理論中賣方在做出決策時要計算出收益的期望值和對應的概率,而在這一過程中買方的行為會影響到互惠所對應的價值和存在的概率,市場決定了金錢、職業前景、所獲得的聲譽等無形收益對應的價值和發生的可能性,管理者則會決定了賣方對交易規定的認可程度,另外所交易知識的復雜程度也會影響到賣方最終提供的出售價格。此外根據上述式子可知賣方進行知識交易的行為不僅會受外部環境的影響,而且還會受到自身的一些條件的影響,例如他自身的偏好、對出售知識的期望等。總而言之,賣方做出交易決策的行為受到外部市場環境和本身一些因素的影響,但是外部環境具備很高的不確定性,而自身的一些因素也會導致他不能獲得充分的信息和做出精密的計算。故而此時的賣方并非完全理性的,不能夠再依據期望最大化的準則做出最有效的抉擇。在學界中也有一些學者經過定量研究發現公司內部職員做出知識共享的決定,不會因為擔心失去專家權力而受到影響,也就是說物質上的激勵并不是總是那么有效的[3]。
? 三、員工知識共享決策的行為經濟學分析
(一)行為經濟學的相關理論
行為經濟學認為人們在進行選擇時,若是存在一些不確定性,那么他們是不能夠理性地進行分析和精確計算各種選擇所對應的概率結果的[4]。因此這一領域的學者提出一些個人模型彌補著傳統經濟學理論中存在的缺陷,進一步解釋了一些經濟現象。
例如Kahneman和Tversky提出了預期理論,按照此理論他們將個體選擇進一步分成了兩個階段,即編輯和評估。在第一個階段個體會對各個選擇做一些信息上的處理,比如將各個選擇所獲得的收益(wi)重新賦值為相對于參照組的收益(w0)所取得的盈余(wi-w0>0)或者虧損(wi-w0<0),這里選擇怎樣的參照組十分重要,它反映現有做選擇的個體現有的財富或者對于將來取得財富的期望,它的選擇一般會考慮沉錨效應和框架效應。所謂沉錨效應實際上反映了人們的一種心理狀態,人們在判斷某種事物往往會受到第一印象的影響,也就是說人們在做判斷時往往喜歡選擇一些參照組。而他們又會根據自己擁有的財富的用途不同將它們劃分成不同心理賬戶,而參照組就是從這些劃分的結果中選擇出來的。框架效應則是說人們在選擇參照組時還會受到選擇的描述和做出選擇的程序等環境因素的影響。
在第二階段個體會根據比較不同決策對應的期望效用(EP),最終做出選擇。所謂EP就是收益對應的效用取值(ui)和其所對應的心理概率(wi)之間的內積的和。我們依據價值函數v(△wi)求得對應的效用值ui(如圖1)。在這一過程中做決策的個體比較關心其相對參照組所獲得的財富是否發生變化,且自身也不喜歡虧損。需要注意的是,若是個體做出決策后獲得了盈余,那么他對待風險的態度是規避,反之若是發生了虧損,他對待風險的態度是偏好。
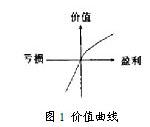
圖1 價值曲線
在依據權重函數π(pi)可以得到wi的過程中(如圖2),做選擇的個體會為小概率發生的事件賦予較大的權重,也就是說π(p)>p,反之則賦予較小的權重,即π(p)

