基于分布式自適應的多智能體容錯一致性控制

張普，薛惠鋒，高山

西北工業大學 自動化學院，西安 710129

目前，多智能體編隊集成了單智能體的大量優勢，并具有廣泛的應用價值，其在軍事領域的應用尤為突出。同時，多智能體編隊在多約束情況下的協同控制、避障、信息融合以及容錯一致性等關鍵技術被大量學者所關注和研究。其中，容錯控制研究在解決實際問題過程中，具有非常重要的地位，也是當前研究的熱點和難點。一致性理論在自主智能體的網絡中，具有典型聚集行為，已經逐漸成為研究的熱點問題[1-3]，包括無人機協同編隊飛行、網絡、機器人編隊、水下無人機編隊等廣泛的應用。內部交互系統是由離散的、一直變化的，并廣泛分布在整個網絡中的多種成分所構成。因此，容錯一致性理論成為解決以上問題的方法。在典型的多智能體系統中，一般是由很多智能體組成一個協同系統，在該系統中，每個智能體僅在分布式結構狀態下對其相鄰的智能體共享其局部信息，進而以一種協同方式去實現全局普遍性行為。

因此，文獻[4-5]采用代數圖論對線性Vicsek模型進行了理論性的研究，得到實現多智能體一致性的充分條件是網絡結構能夠在有限的時間內頻繁的連接。同時，還提出了一種有效的一致性結構用于解決復雜網絡中多智能體的一致性和同步性問題。文獻[6-7]均采用基于拓撲結構的智能體編隊信息交換機制對編隊進行控制，使得系統也能達到漸進一致穩定。文獻[8-10]提出了一種分布式自適應一致性方法，用于克服智能體之間不同步的局限性，在一致性控制器設計中需要知道圖論中拉普拉斯矩陣的特征值，這個特征值實際上是智能體系統的整體信息。文獻[11]給出了二階系統一致性理論在多智能體中的充分必要條件，充分證明了一致性方法的優勢。文獻[12]對國內外多智能體技術的應用進行了闡述，分析了多智能體一致性及控制的關鍵技術，并指出目前亟需解決容錯一致性問題。對于多智能體編隊系統的研究，當子系統的數目較少且通訊正常的情況下，可應用集中式控制方法解決多智能體協同編隊運動。然而，對于一個多智能體系統而言，當有個別智能體逐漸老化或者出現故障時，在這種情況下，由于系統中單個智能體具有特定的作用，不能輕易取而代之。而且不同智能體出現老化或者故障的程度不同，可能導致增加修復的成本。因此，本文提出了分布式自適應下的容錯控制研究，主要解決2個問題：① 系統中單個智能體發生故障或者環境不確定，智能體仍能完成任務；② 智能體系統發生故障時，設計分布式容錯控制器及時補償故障誤差，使其快速恢復正常的工作狀態。

在過去幾年里，在對系統進行故障分析時，由于網絡系統的復雜性和時實系統的安全需要，很多學者已做了大量研究去解決網絡系統和執行機構中的故障問題。例如，文獻[13]對延遲系統進行了故障估計研究，此后，復雜系統的故障診斷和檢測有了一定的進展。文獻[14]對一種廣義非線性系統的執行器進行了容錯控制研究。文獻[15]研究了單一系統的容錯控制服從于執行器飽和非線性擾動的影響。文獻[16]對于一類非線性系統設計出了一種容錯控制結構。文獻[17]設計了一種容錯控制適用于一類非線性樣本數據系統。文獻[18]將容錯控制應用于實際工程中，解決了無人機的執行高負荷以及長航時旋翼疲勞斷裂導致其失控甚至墜毀不能完成作戰任務的問題，具有實際的應用價值。Yoo針對無人機編隊中任意一架無人機的執行機構故障，在不確定外界環境條件下，設計了一種反步容錯控制，有效地解決了無人機編隊飛行中的容錯控制問題[19]。文獻[20-21]研究了四旋翼無人機在運動過程中執行機構容易發生故障影響飛行品質問題，提出了執行器故障下四旋翼無人機的容錯控制估計方法，為后續研究提供了充足的理論支撐。魁北克大學Ghommam等[22]采用反步法，設計了基于局部相對信息的分布式控制器，實現了多無人機的有效跟蹤，仿真實驗驗證了該算法的有效性。但是，作者并沒有考慮系統的輸入飽和因素，這不利于工程實踐。文獻[23]針對多個歐拉系統分布式編隊牽制問題以及模型的不確定性，提出了一種輸出反饋控制方法。然而，該成果未考慮避障情況和通訊時延的約束。綜上所述，容錯控制的發展非常迅速，并主要用于解決大量的實際應用問題。

盡管在現有文獻中，一些有效的容錯控制已經得到了發展，但在多智能體系統的研究中仍有一些問題亟待解決。總體上，多智能體系統已在生態系統、傳感器網絡以及機器人編隊等方面得到了應用。然而，隨著溫度和設備年限的增加以及不可避免的能量損失等因素都能夠引起故障的發生。因此，需要針對多智能體編隊中個別單智能體出現故障問題，設計一種新的自適應一致性協議，解決以上問題。

為了解決多智能體容錯控制一致性問題，相對于文獻[19]，本文的主要創新點和主要工作為：① 在分布式一致性控制領域中，基于“領航者-跟隨者”編隊模型考慮多智能體中領航者模型的非線性和量化輸入特性；② 所設計的控制律不需要領航者的位置信息和速度信息以及任何自適應函數逼近器的信息補償自身的故障所帶來故障誤差；③ 設計了一種離線情況下的自適應容錯控制器，能夠實現多智能體的橫向距離誤差減小70.58%，縱向距離誤差減小87.09%，同時橫向和縱向的動態收斂時間分別減小44.12%和25.85%。因此，所提出的控制方法能夠對信號的擾動進行及時處理，并對故障后的編隊系統進行實時補償控制，達到快速編隊運動的目的。

1 建立模型

1.1 圖 論

一個加權無向圖G=(V,ε,A)由非空頂點集V={v1,v2,…,vN}和邊緣集ε={eij=(vi,vj)}以及一個加權鄰接矩陣A=[aij]N×N組成。其中，aij為非負元素，且aij>0，它是節點vi和vj之間的邊，另外，當aij=0，表示節點vi和vj之間沒有邊。節點vi的鄰邊由Ni={vi∈V:(vi,vj)∈ε}指代。在圖G中節點vi和vj之間的路徑是一系列邊(vi1,vi2),(vi2,vi3),…,(vil-1,vil)。如果圖G是連通的，則圖G中任何節點vi和vj，存在一條路徑vi和vj(i,j=1,2,…,N)[1]。

拉普拉斯矩陣L=[lij]∈RN×N定義為

(1)

1.2 數學模型

本文多智能體編隊系統由4個智能體構成，其中智能體1作為領航者，其余智能體作為跟隨者。同時，智能體1的速度方向作為編隊前行方向，其余智能體緊跟其后。多智能體運動示意圖，如圖1所示。

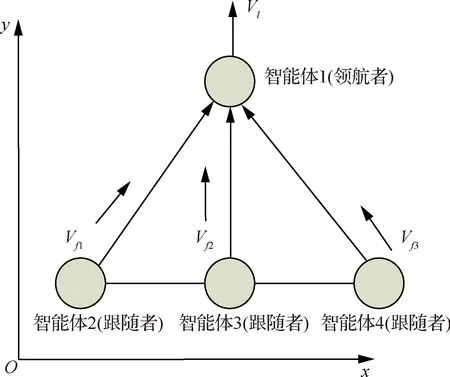
圖1 多智能體編隊運動示意圖Fig.1 Formation movement of multiple agents

本文中，考慮了一組N(N=4)個具有相同特性的線性動力學智能體。第k個智能體的動態方程為

(2)

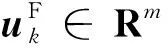
為了解決容錯一致性問題，首先建立了故障模型。在本文中，考慮故障時的執行機構模型[22]，其一致性控制協議為

(3)

式中：qk為未知執行器的故障因子，代表了第k個智能體的故障。

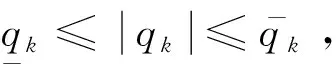
對于任意u∈R且ε>0[24]，有

(4)

式中:k=0.278 5。此外，對于Riccati方程，滿足矩陣P正定，即

(PA+ATP)-PBBTP+In=0

(5)

式中: 存在P正定且(A，B)是穩定的，同時他們之間的運算滿足克羅內克積。In代表了N階單位矩陣。1N∈RN指的是所有的列向量都為1。同時，令PB=Q。

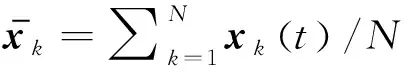
(M?In)(ΘΩ(t)L?BBTP)z+

(QΘ?In)(IN?B)f(t,x)

(6)

為得到智能體的不確定模型，給出以下假設：

假設1 第k個智能體的不確定性：

[g1(t,xk(t)),g2(t,xk(t)),…,gm(t,xk(t))]T

滿足：

(7)

式中:αk和βk是未知常量，(c1,c2)∈(0,1)是權重系數。

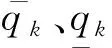
假設3 在智能體編隊中，領航者和跟隨者之間的通訊是通暢的。

2 控制器設計

針對系統(2)中，領航者一旦出現故障，設計分布式自適應容錯控制器能夠有效快速地補償故障影響，并完成預設的任務。其控制律為[25]

(8)

式中：bk為第k個智能體的權重系數，且當與鄰近的智能體有信息交互，則bk=1，反之為零。

(9)

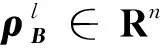
備注2 式(8)中uak表示智能體故障補償控制律。當領航者出現故障時，其模型的未知擾動項g(t,xk(t))為非線性函數，需要減小或消除這種未知擾動項，才能使系統快速達到穩定狀態。

證明 令未知擾動項g(t,xk(t))=S1(非線性函數)，控制項uk=S2(非線性函數)。

當多智能體中領航者出現故障時，自適應控制項uk必須滿足以下關系：

uk=g(t,xk(t))

(10)

S1+S2?0

(11)

此時，所設計的控制協議能夠減小或消除這種未知擾動。

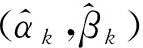
對于第k個智能體的一致協議增益更新率ωk為

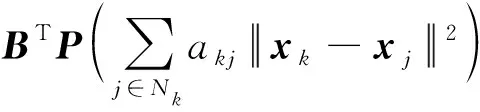
(12)

式中:dk1、dk2為正常數。

(13)

式中:

(14)

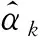
(15)

(16)

(17)

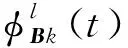
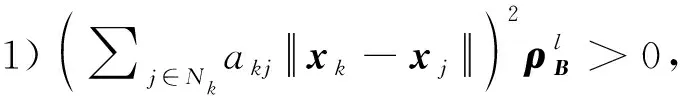
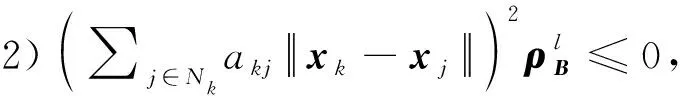
該性質用于式(15)和式(16)參數的更新，為式(9)中自適應容錯一致性控制器的設計提供理論支撐。在多智能體中，領航者出現故障后，所設計控制器能快速實現補償，達到穩定狀態的具體步驟為

步驟1 每個智能體的傳感器用來感知和搜索鄰近信息。

步驟2 每個智能體中的參數通常是更新的，這些參數根據式(15)和式(16)中的更新率來監測和調整。

步驟3 觸發器能夠使用這些參數去補償式(9)中所控制的每一個智能體，最終使所有的智能體實現一致性的目的。

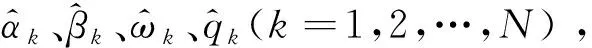
(18)

3 穩定性分析

構建李雅普諾夫函數，即

(19)

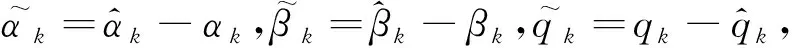
對式(19)時間求導，有

(20)

將式(6)代入式(20)可得

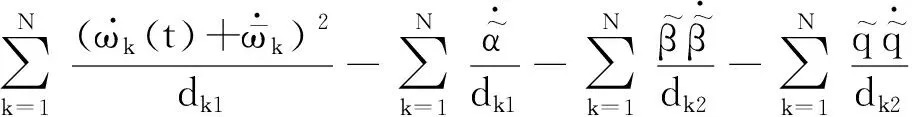
(21)

(22)

由式(9)～式(22)，可知：

zT(t)(LΘ?PB)uak+zT(t)(L?PB)f(t,x)=zT(t)(LΘ?PB)uak+zT(t)(L?PB)·

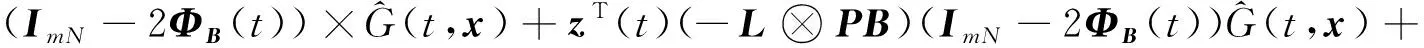
(23)

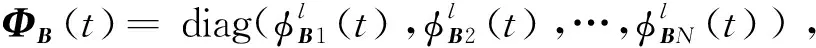
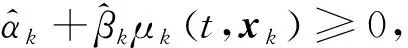
(24)

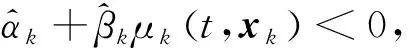
(25)

(26)

根據不等式(24)～(26)，可得

(27)

(28)

結合不等式(23)和(27)，代入式(13)中的更新律，可以得到

(29)

進一步，可得

zT(t)(LΘΩ(t)L?PBBTP)z+

uak+zT(t)(L?PB)f(t,x)+

zT(t)(-L?PB)(ImN-2ΦB(t))·

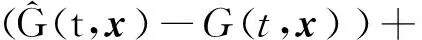
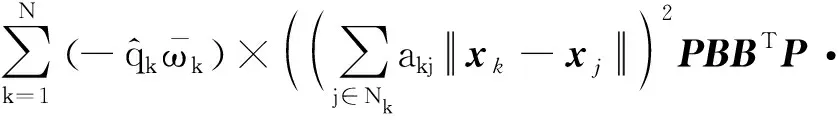
(30)

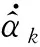
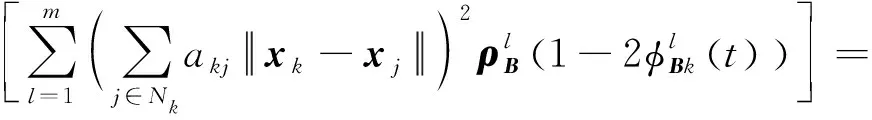
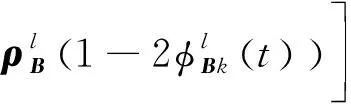
(31)

通過選擇足夠大的ω滿足2ωλi≥1(i=2,3,…,N),同時根據式(5)，可以得到

(32)

令ζ=1/λmax(P)，同時選擇kαk=ζ，kβk=ζ，其可以進一步簡化為

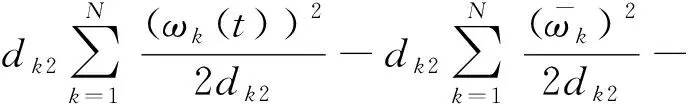
(33)

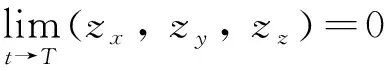
證明 由式(3)可知，智能體故障模型控制協議如下：

(34)

式中：mk為正常數。

假設故障因子qk=a(a為常數)，則誤差動力學模型，可進一步化簡為

(MΘ?B)uak+(M?B)f(t,x)

(35)

當多智能體經過時間t，達到既定的隊形并保持，則誤差z等于零，即z=0。因此，式(35)可簡化為

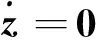
(36)

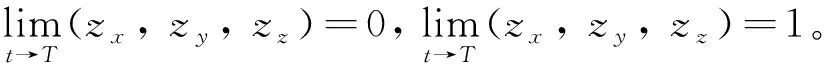
4 仿真驗證

在本文中，多智能體編隊由4個智能體構成，他們具有相同的特性。為了驗證所設計分布式自適應容錯方法在領航者出現故障的情況下多智能體編隊運動的有效性和穩定性，本文基于系統模型(2)進行數值仿真。同時將文獻[19]和本文所提出的方法進行對比分析，進一步驗證所提方法的優勢所在。根據圖1，本文考慮具有4個節點的多智能體系統，同時模型(2)系統矩陣A∈R4×4，B∈R4×2。

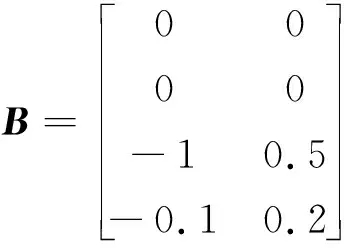
根據圖論，可得多智能體編隊系統的拉普拉斯矩陣L，即

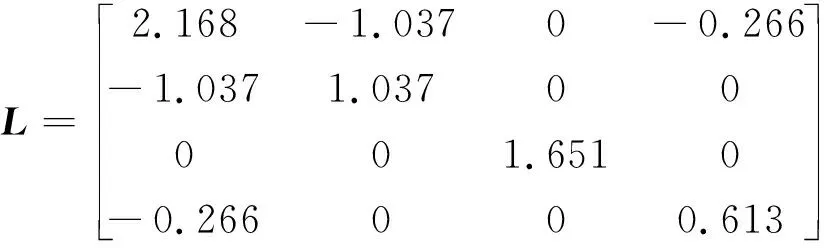
(37)

采用MATLAB解式(5)，可得矩陣P，即

(38)

考慮多智能體編隊系統出現故障，即

(39)

式中：αli表示領航者的故障系數，(αl1,αl2,αl3,αl4)=(0.214，0，0，0，0)，βfi表示跟隨者的故障系數，(αf1,αf2,αf3,αf4)=(0.345 2, 0.547 4, 0.321 4, 0)。同時，考慮多智能體模型容錯參數估計，即

(40)

其他初始值為

k=1,2,3,4，ζ=1/λmax(P)=1.081 1

4.1 收斂性分析

基于以上的假設和初始條件，對所提出方法在多智能體編隊的運動收斂性進行分析。其仿真結果如圖2～圖4所示。

圖2給出了多智能體縱向距離誤差曲線圖。由圖可知，隨著時間變化，該曲線呈現出一種智能體2和3緩慢下降，智能體1和4緩慢上升，之后均趨于穩定狀態。0～10 s，智能體2和3在前，智能體1和4在后，并追趕智能體2和3。在領航者出現故障后，自適應算法啟動，智能體2和3減速，智能體2和4加速，使得他們與期望位置的誤差逐漸減小至穩定狀態；10 s后，多智能體編隊系統按照 “領航者-跟隨者”編隊模式運動。

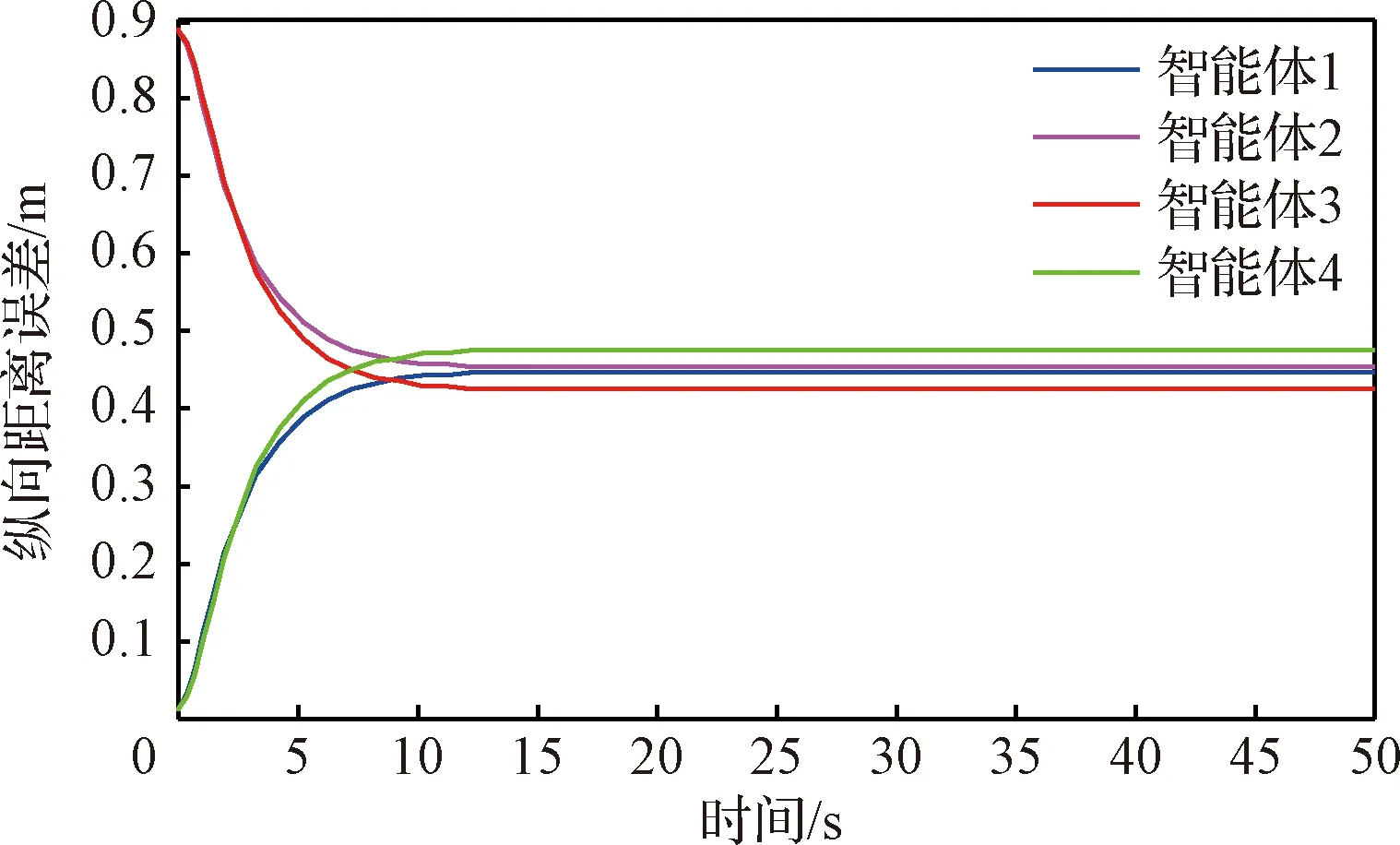
圖2 縱向距離誤差曲線Fig.2 Curves of longitudinal distance error

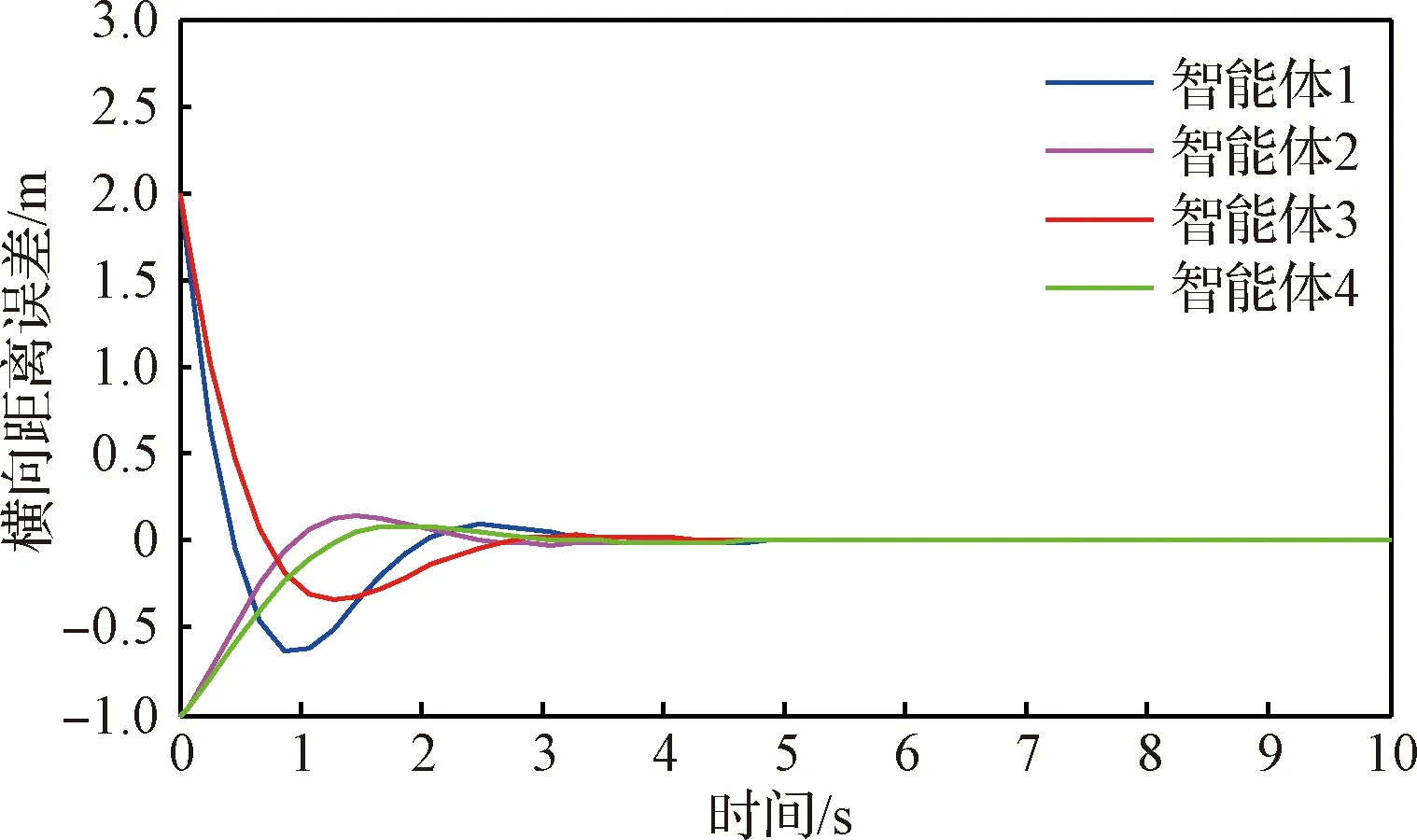
圖3 橫向距離誤差曲線Fig.3 Curves of lateral distance error

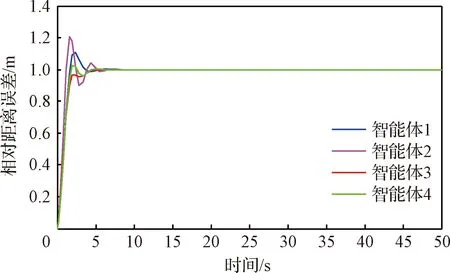
圖4 “領航-跟隨”相對距離誤差曲線Fig.4 Curves of relative distance error for “leader-follower”

圖3給出了多智能體橫向距離誤差曲線圖。由圖可知，隨著時間變化，該曲線呈現一種智能體1和3快速下降，智能體2和4緩慢上升，且智能體2和4小幅振蕩，之后均趨于穩態。在1 s時，智能體1和3的橫向距離誤差已達到最小，此時智能體2和4基本趨于零，這是由于智能體1在0.9 s時出現故障，此時自適應容錯算法立刻啟動，該曲線緩慢上升并迅速趨于穩定；在3 s之后，4個智能體橫向距離誤差收斂于零，保持預設的隊形運動。

圖4給出了“領航者-跟隨者”智能體編隊系統的相對距離誤差曲線圖。由圖可知，隨著時間的變化，該曲線呈現一種先快速上升，然后小幅振蕩直至趨于穩態的趨勢。在0.9 s之前，曲線呈現一種快速上升，這是由于跟隨者以不同的速度追蹤領航者，智能體間的距離增大；在領航者出現故障后，該曲線呈現波動趨勢，這是由于在0.9 s之后智能體處于從即將到達預設的隊形到期望的隊形之間的微調整階段，即領航者需保持速度，而跟隨者需減速；在5 s之后，曲線趨于穩定狀態，并4個智能體的速度和相對位置保持一致。

4.2 魯棒性分析

為了進一步驗證所提出自適應控制方法的魯棒性，本節采用相同參數進行仿真研究。由于多智能體編隊在平面內運動，本節針對所設計的分布式自適應容錯方法在橫向和縱向因領航者出現故障補償后的跟隨者的追蹤距離誤差進行對比分析，如圖5～圖7所示。

圖5給出了智能體縱向追蹤距離誤差曲線圖。由圖可知，隨著時間的變化，該曲線呈現一種先快速下降，而后緩慢上升，直到穩定狀態。在0.9 s之前，該曲線呈現快速下降趨勢，這是由于他們的初始位置和速度均不相等，在集結過程中，他們之間的縱向距離逐漸縮小，且智能體4的速度減小最大；在1～3.5 s，曲線呈現緩慢上升，這是由于領航者出現故障，自適應算法啟動后，智能體達到預設的隊形之前處于微調整階段，而且跟隨者幾乎收斂于領航者的飛行軌跡。在6 s之后，多智能體之間的相對位置和速度保持一致同時確保避障。

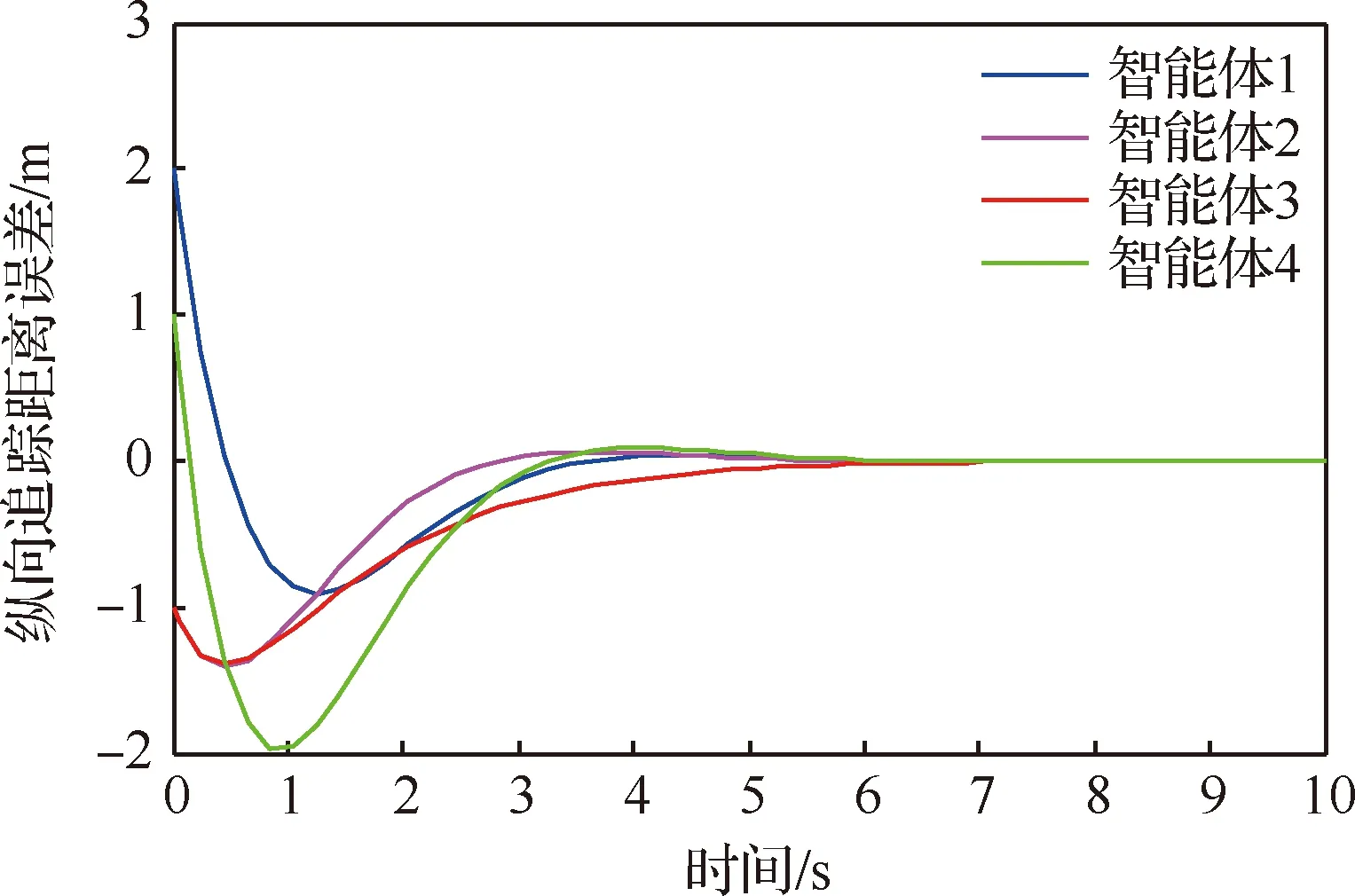
圖5 智能體縱向追蹤距離誤差收斂圖Fig.5 Convergence diagram of longitudinal tracking distance error of agent

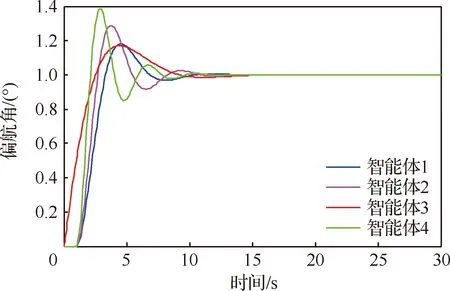
圖6 “領航-跟隨”編隊偏航角指令曲線Fig.6 Command curves of yaw angle of “leader- follower” formation

圖7 多智能體偏航角速率曲線Fig.7 Curves of multi-agent yaw angle rate

圖6給出了“領航者-跟隨者”編隊系統的偏航角指令曲線。由圖可知，隨著時間的變化，該曲線呈現先快速上升，后小幅振蕩直至穩定狀態。在多智能體編隊系統運動過程中，因領航者出現故障，為了補償或者消除這種故障影響，所提出的分布式自適應容錯控制算法可以確保在故障情況下，正常編隊運動。在0.9～3 s之前，領航者在前，跟隨者在其后，跟隨者追蹤領航者過程中，速度方向指向領航者，此時偏航角增大。智能體1的偏航角達到1.4°，即將達到預設隊形，此時需減小偏航角防止發生碰撞；在4～10 s，4個智能體處于即將達到預設隊形微調整階段，此時領航者減小，保持一個常值，其余跟隨者微調其偏航角保持預設隊形運動；在12 s之后，4個智能體處于穩定狀態。

圖7給出了多智能體偏航角速率曲線圖。隨著時間的變化，該曲線呈現一種快速上升后，趨于穩定狀態。在集結預設編隊之前，智能體編隊系統縮小之間的相對距離；在即將達到預設隊形時進行微調整，然后保持速度和相對位置的一致性穩定運動。由圖7可知，4個智能體的偏航角速率的變化量分別是0.43、0.11、0、0.10 (°)/s，穩態所需時間分別為5、4.2、4.21、2.5 s。易得，在0.9 s，智能體1為領航者出現故障，此時所設計的容錯控制算法啟動，使其在2 s調整至正常運動狀態，直至6 s后保持一致協同編隊運動。

從以上分析可知，多智能體編隊系統中領航者出現故障時，所提出的分布式自適應容錯控制方法能夠補償故障帶來的損失，保持系統正常運行。而且，該方法動態響應快，追蹤誤差效果好。

4.3 可行性分析

為了進一步驗證所提出方法的可行性和優勢性，本節采用相同的系統模型，初始條件以及相關參數，將所提出的方法和文獻[19]在橫向距離誤差和縱向距離誤差以及達到穩定所需的收斂時間進行對比分析，仿真結果如圖8和圖9所示。

圖8給出了多智能體橫向距離誤差對比曲線圖。由圖可知，隨著時間變化，文獻[19]中的方法的橫向距離誤差曲線呈現一種先迅速上升，后緩慢下降直至趨于穩態，而本文所提出的方法的橫向距離誤差曲線呈現一種迅速上升后趨于穩態。同時，文獻[19]和本文方法的橫向距離誤差分別為0.17、0.05 m；相應的達到平衡狀態所需時間分別為3.4、1.9 s，由此可知本文所提的控制方法，穩態誤差小，動態響應快，有利于容錯補償控制。

圖9給出了多智能體縱向距離誤差對比曲線圖。文獻[19]所提方法的縱向距離誤差曲線，隨著時間變化，呈現一種快速上升，然后緩慢下降，之后又小幅震蕩，直至緩慢達到穩定狀態，而本文所提出的控制方法的縱向距離誤差曲線呈現緩慢上升后迅速達到穩定狀態。文獻[19]和本文方法縱向距離誤差分別為0.31和0.04 m，相對應達到穩態的時間分別為32.5和24.1 s，顯然易知，本文所提出的控制方法，不但可以使領航者受損的多智能體編隊系統恢復正常的運動狀態，而且能夠快速達到預定的隊形，同時保持隊形不變。

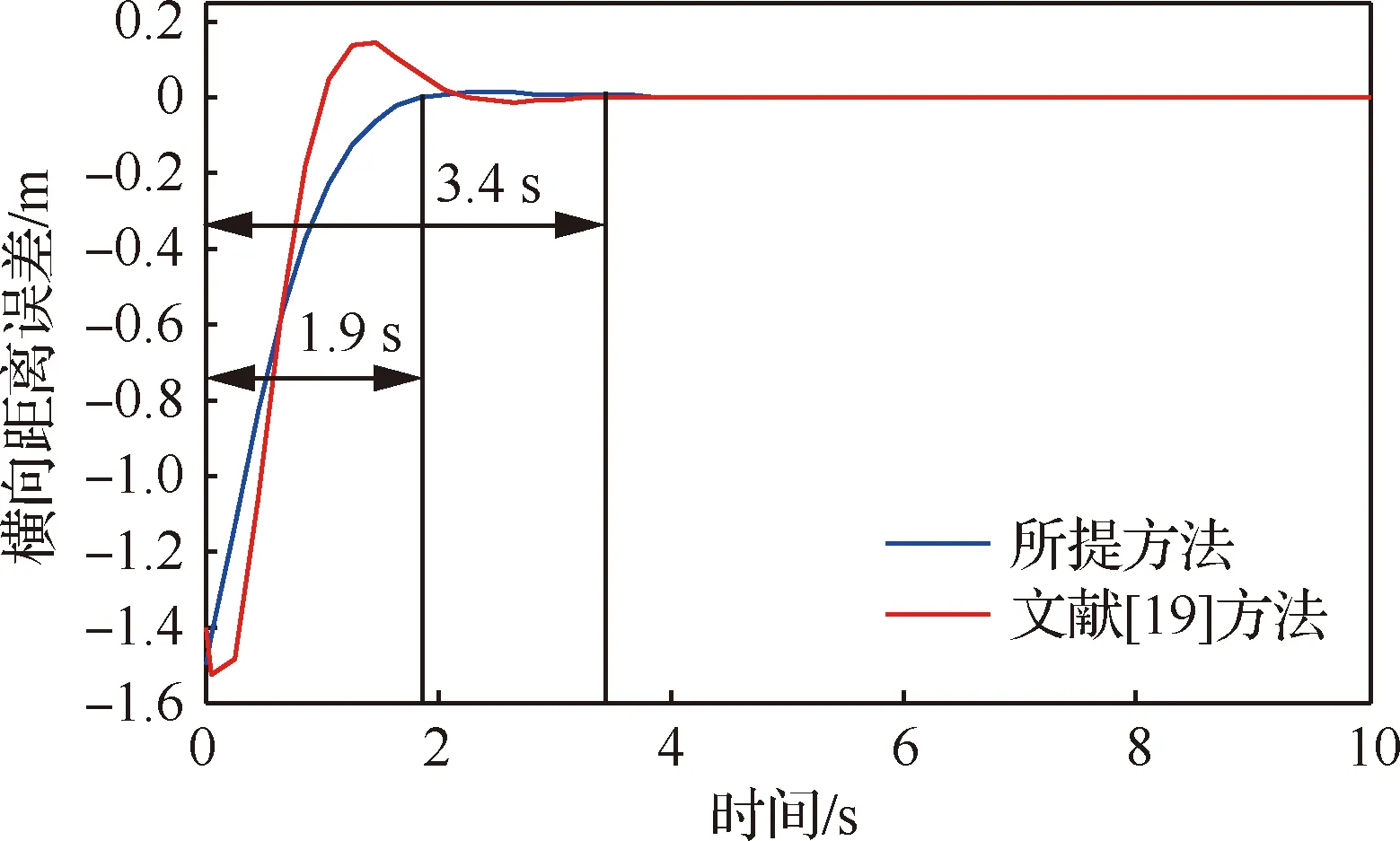
圖8 橫向距離誤差對比Fig.8 Comparison of lateral distance errors

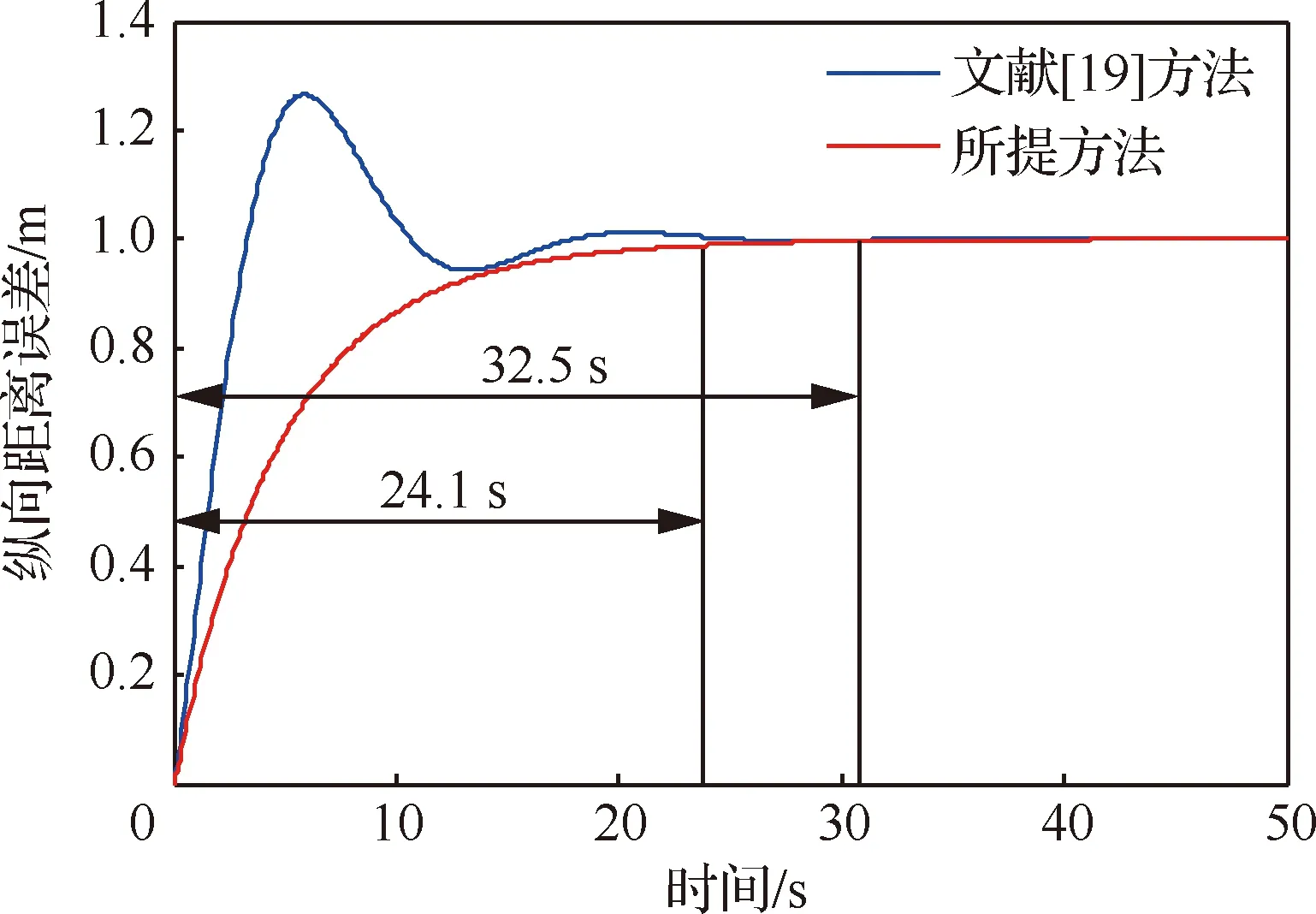
圖9 縱向距離誤差對比Fig.9 Comparison of longitudinal distance errors

根據文獻[19]和本文所提出的方法對應的橫、縱向距離誤差以及相對應收斂時間，將其匯總，如表1所示。

由表1可知，本文所提出的方法不僅在橫向距離誤差小，響應時間短，而且在縱向距離誤差更小，響應時間更短，對于多智能編隊系統的容錯補償更有利。

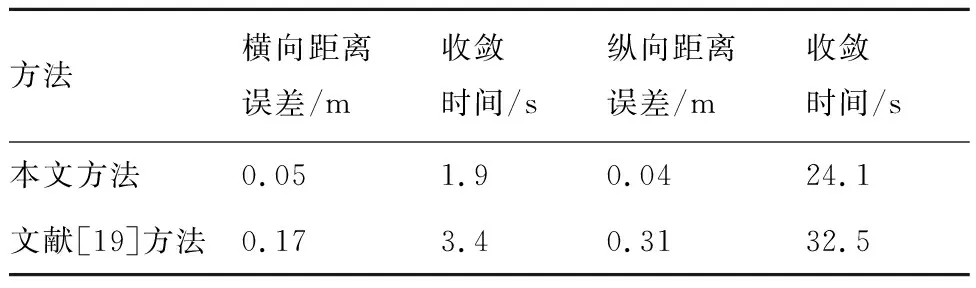
表1 橫、縱向距離誤差以及收斂時間

5 結 論

基于一致性理論，本文提出一種分布式自適應容錯控制方法，該方法采用李雅普諾夫穩定性理論對其進行了證明，并通過數值仿真實驗驗證了該方法的收斂性和魯棒性。主要結論如下：

2) 如果多智能體故障發生在集結預設隊形之后，通過本文相關理論推導，易知多智能系統是穩定的，即使發生故障，所提出的方法也不能實現容錯控制。因此，本文所研究的被控對象有相應的約束條件。

3) 本文是以多智能體最小研究單元作為被控對象，即4個智能體，并采用所提出的方法進行容錯控制。同時所提出的方法適用于數目小于10的多智能體編隊。

然而，本文僅考慮多智能體從不同起點以不同速度出發到集結預設隊形過程中容錯控制，每個智能體視為質點處理，未考慮測距傳感器的精確等，下一步工作將在縮比模型上進行試驗以驗證所設計的控制方法的可控性和有效性。