基于增量成本一致性的孤島微電網分布式下垂控制

張朝霞，文傳博，蔡鵬程

（上海電機學院 電氣學院，上海 201306）

0 引言

微網是由分布式電源（Distributed Generation，DG）、儲能裝置、負荷和控制裝置等組成的獨立供電系統，可以并網和孤島運行[1]～[4]。孤島運行時，通常采用基于下垂控制的多機并聯運行方式承擔負荷分配，按照額定容量分配有功功率，未考慮分布式電源的運行成本，易使微電網的運行成本偏高。在微網穩定運行條件下，微網運行成本成為了目前的研究熱點[5]～[7]。

微電網二次控制可分為集中式控制、 分散式控制和分布式控制。 集中式控制對通信線路的依賴程度較大，并可能存在單點故障，可靠性較差[8]。分散式控制很難實現各分布式電源之間的協調運行[9]，[10]。 分布式控制僅依靠局部弱通信就可以實現各分布式電源間的協調控制[11]。 由于傳統下垂控制會出現頻率偏差，文獻[12]提出了頻率自恢復和實現有功功率共享的孤島微網分布式控制方法。 文獻[13]針對線路呈阻感特性使低壓微網的功率嚴重耦合，提出了在下垂控制加虛擬負阻抗的方法改善無功補償與線路壓降的問題。 文獻[14]在傳統下垂控制中，加比例積分與前饋調節改變下垂系數，從而實現負荷的按需分配。 文獻[15]，[16]利用不同的條件和環境，對微電網的頻率使用不同的方法進行研究和控制。 以上文獻只考慮了分布式控制中電壓、功率與頻率的控制，均沒有考慮各分布式電源的運行成本問題。 文獻[17]將各DG 的增量成本作為一致變量，提出基于一致性算法的分布式調度策略。 文獻[18]針對微電網中并聯分布式發電單元間功率分配精度差、運行成本高等問題，提出了基于分布式算法的改進經濟下垂控制策略，通過增加二級優化控制，達到了調節功率經濟運行的目的。 文獻[19]針對微網經濟運行中功率分配精度問題，提出了分層控制策略，通過三級控制減少電壓波動，實現微網功率的最優分配。 以上文獻雖考慮了各分布式電源的經濟性問題，但很少考慮優化運行控制問題，并且信息交互中未涉及具體的通信過程，缺乏實際應用的支撐。

本文在已有研究基礎上，提出了一種基于多智能體系統（Multi-Agent Systems，MAS）增量成本一致性的分布式下垂控制策略。 該策略采用兩層控制結構，上層是基于MAS 的通信網絡，下層是基于下垂控制的微網。基于此模型，提出增量成本一致性算法，優化下垂控制的參考頻率，實現微網運行成本的最小化。 該策略只需智能體之間局部通信，克服了無通信線下垂控制與集中控制的弱點，可靠性高。 最后，本文對所提算法的收斂性進行了證明，并通過Matlab/Simulink 仿真，驗證了控制策略的有效性。

1 基于增量成本一致性的分布式下垂控制

1.1 增量成本一致性算法

傳統的最優增量成本 （Incremental Cost，IC）由集中控制器計算，存在單點故障和通信開銷大的問題。 因此，本文選擇增量成本作為一致變量，以分布式的方式求解經濟優化問題。 在分布式控制一致網絡中，每個分布式電源將根據其鄰居的增量成本更新自己的增量成本。此外，選擇一個機組作為領導者（Leader）機組，其他機組為跟隨者機組。 根據系統的變化，降低或增大系統全局的IC，即當發電機總輸出功率大于負荷總需求功率時，就會降低全局的IC，反之亦然。

與傳統經濟調度方法相同，在增量成本一致性算法中，各DG 的增量成本定義為

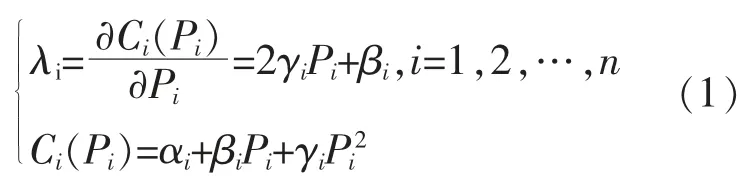
式中：λi為發電單元 i 的增量成本；αi，βi，γi為發電成本參數。

在沒有發電容量約束的情況下，當增量成本達到一致時，可以實現最小發電成本的目標，共同的最優解為λ*，目標輸出功率為

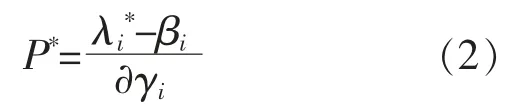
本文提出各發電單元的增量成本一致迭代為

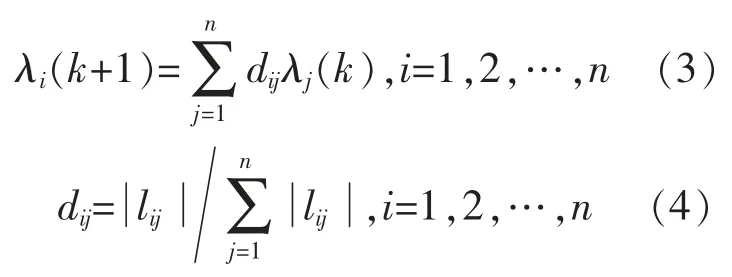
式中：dij為行隨機矩陣 Dn的（i，j）項對應的權值，且式（3）是對應著跟隨者節點的更新規則。

遵循式（3）系統將會收斂到一個共同的增量成本，收斂速度基于系統通信網絡的拓撲結構。此外，為了滿足功率平衡約束，本文提出并定義ΔP為全局功率供需不匹配，且

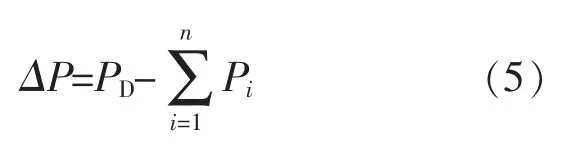
領導者節點的更新規則為

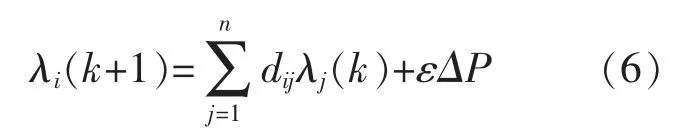
式中：ε 為收斂系數，是正極性的標量，控制系統整體的收斂速度。

式（3），（6）是增量成本一致性算法的數學表達式。 因此，在分布式控制策略中，所提出的增量成本一致性算法的更新規則為

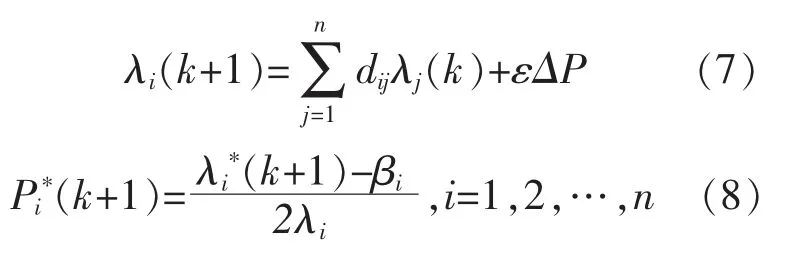
式中：λi（k）為 DGi在第 k 次迭代的增量成本。 輸出功率Pi也在增量成本一致性算法中進行更新。

1.2 分布式下垂控制

微網孤島模式運行時，傳統的P-f 下垂控制將根據各發電單元額定功率Pni與下垂系數mi分配有功功率，不能夠達到理想的負載優化分配，并且系統穩定時，頻率將會偏離額定值。

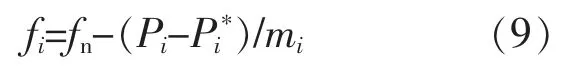
在微網中各DG 的輸出頻率fi必須相同，且各額定頻率fn都為50 Hz，因此fi-fn為常數。令fifn=k，則由供需平衡關系可知因此由 mi>0 可知，k=0，即從而可得 fi=fn。 因此，所提控制策略能夠實現負載的優化分配，也保證孤島模式下，微網頻率穩定在額定值。

本文設計的分布式下垂控制結構如圖1 所示。

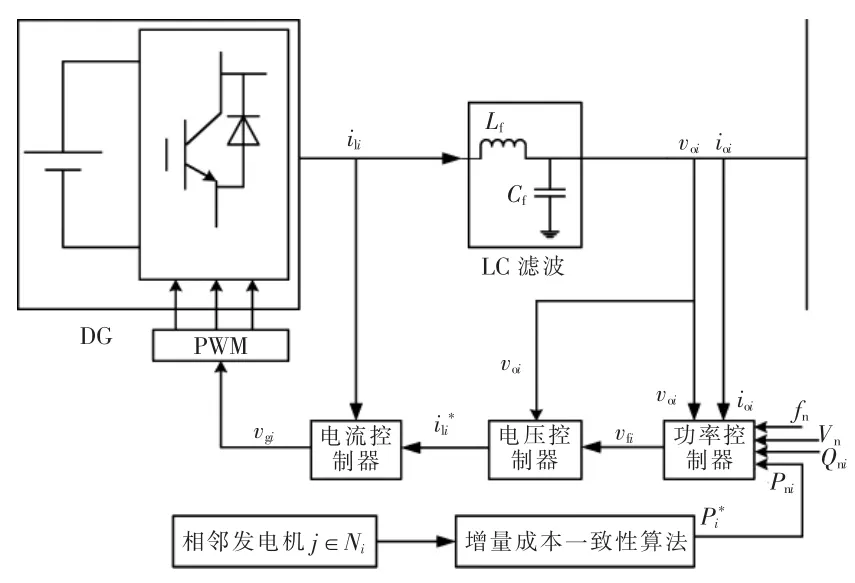
圖1 優化下垂控制結構圖Fig.1 Optimized droop control structure diagram

由圖1 可知，通過增量成本一致性算法對功率值進行更新，得出最優發電量。 由功率控制器計算逆變器輸出的功率值，并依據下垂特性得出電壓控制環的期望值。

2 仿真與分析

為驗證本文所提基于增量成本一致性的分布式下垂控制策略的有效性，在Matlab/Simulink 仿真環境下進行仿真分析。 系統仿真所用的微電網系統結構如圖2 所示。 選擇DG1 為領導者節點（主電源），用于直接獲得供需不匹配量。

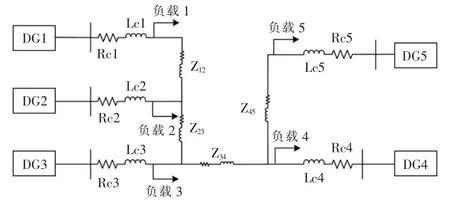
圖2 孤島交流微電網仿真結構Fig.2 Structure of island AC microgrid simulink

測試系統有5 個DG，每個DG 的局部負載的額定有功功率分別為2P1=P2=P3=P4=2P5=20 kW。有功功率值的上限分別為 20，30，30，30，20 kW；下限分別為 0.5，1，1，1，0.5 kW。 測試系統的相電壓幅值為311 V，頻率為50 Hz。 系統的通信拓撲結構如圖3 所示。

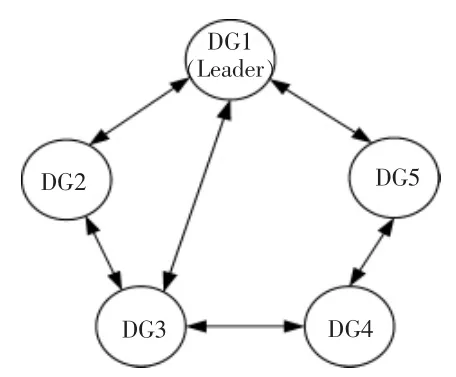
圖3 微電網通信拓撲結構Fig.3 Communication topology structure of microgrid

該微電網系統對應的行隨機矩陣為

仿真系統中，各DG 的成本參數如表1 所示，各DG 的控制參數如表2 所示。

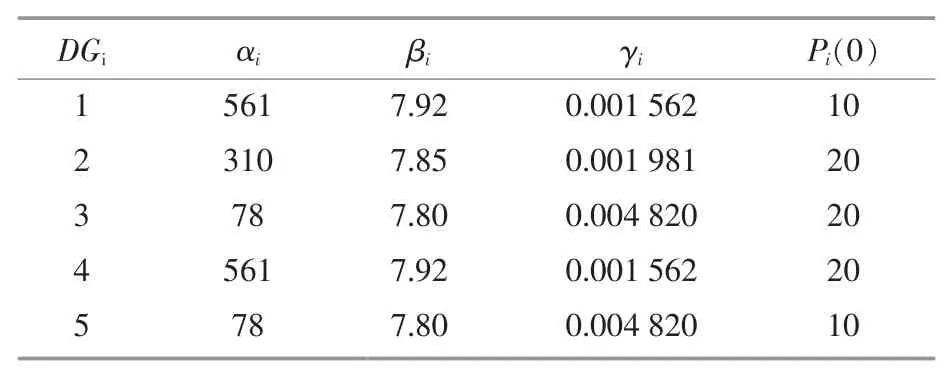
表1 各發電單元成本參數Table 1 Generator cost parameters

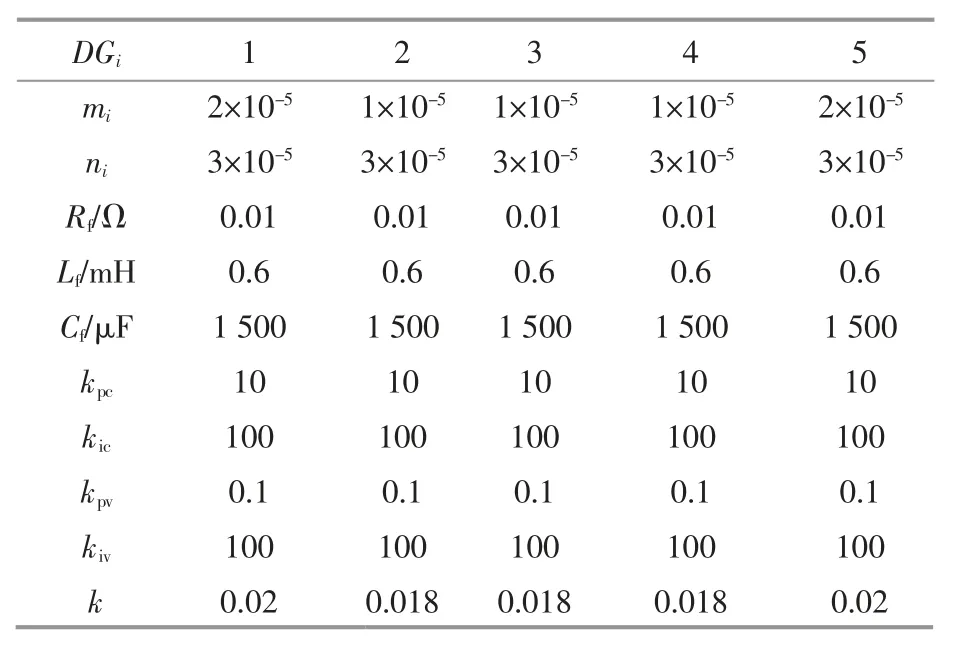
表2 系統仿真控制參數Table 2 Simulink control parameters

2.1 算法的收斂性仿真

在控制系統中，不同的通信網絡對應的拓撲結構也不同，算法的收斂速度與系統的拓撲結構密切相關，選擇合適的拓撲結構對算法的收斂性以及系統的優化控制效果至關重要。 本文給出了由5 個節點組成的3 種不同拓撲結構的通信網絡，如圖4 所示，仿真結果如圖5 所示，來驗證分析拓撲結構對算法收斂性的影響。 其中DGi（i=1，2，3，4，5），以作為收斂判據，其中，ci為DGi的增量成本，cc為增量成本的收斂值。

由圖3 中的3 種不同通信網絡的仿真收斂情況可以看出，只要通信拓撲對應的拉普拉斯矩陣滿足行隨機，算法最終都會達到收斂，趨于一致。

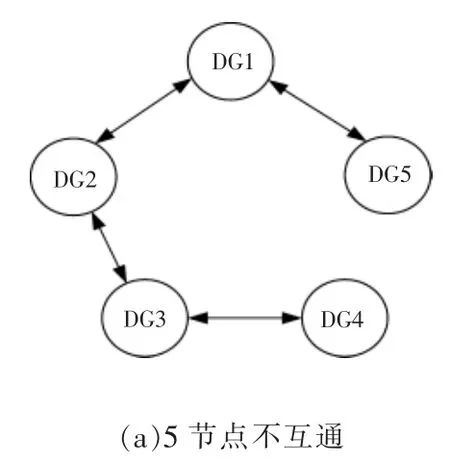
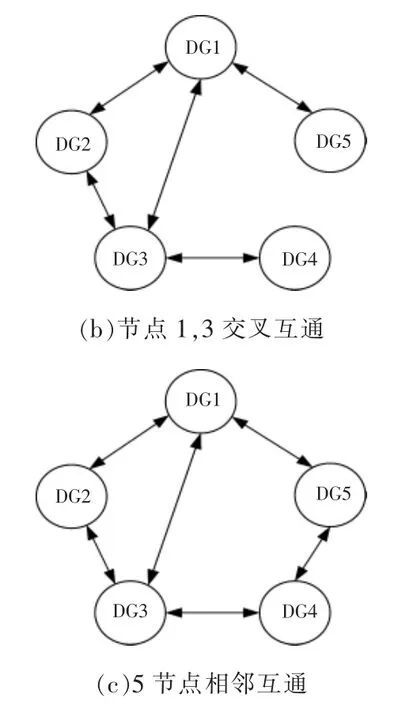
圖4 不同通信網絡Fig.4 Different communication networks

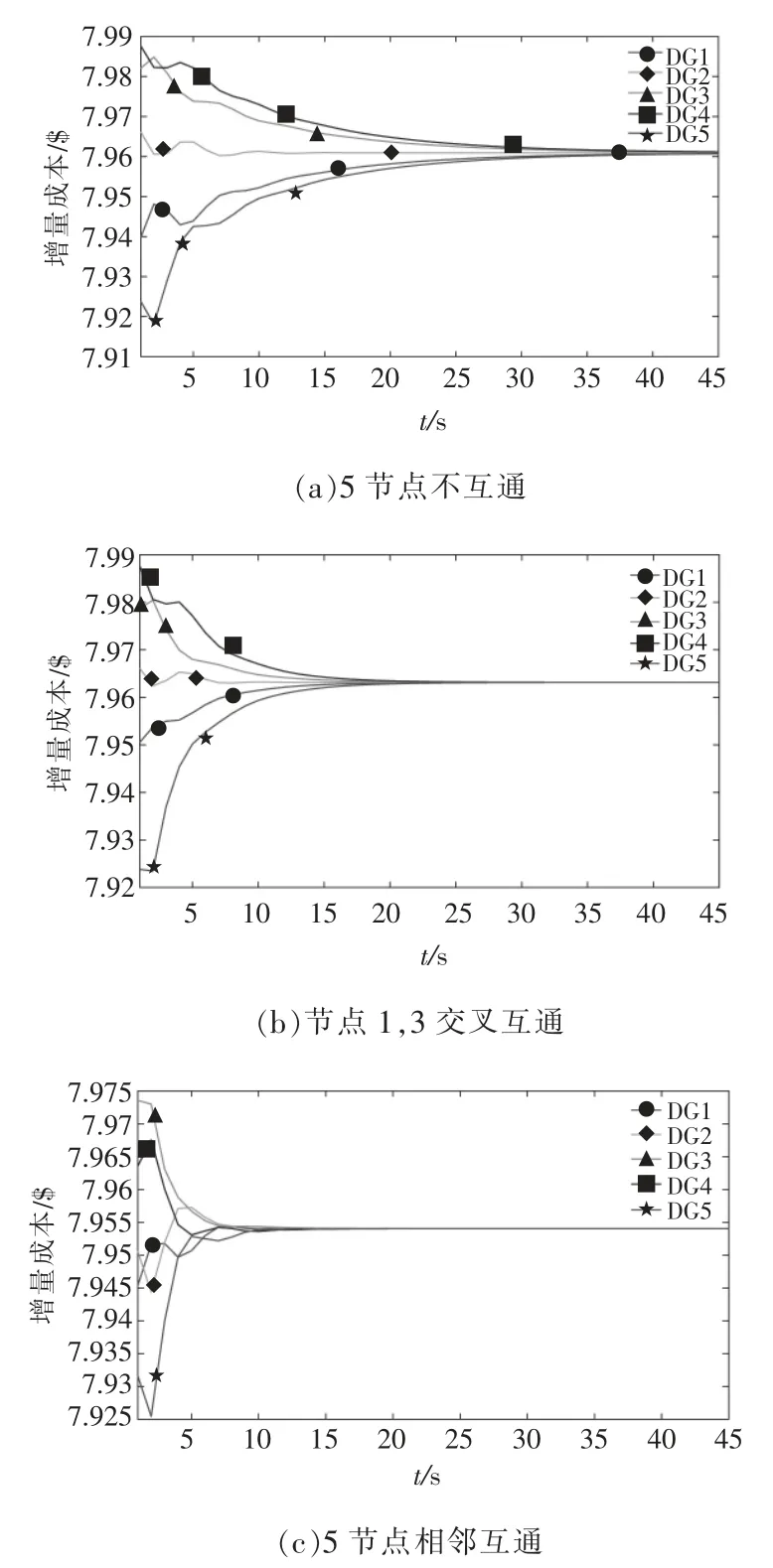
圖5 不同通信網絡的仿真Fig.5 Simulation of different communication networks

由圖4 可以看出，隨著通信線路的增加，系統的收斂速度越快。由圖5 可以看出，隨著通信線路的斷開，雖然系統的收斂時間會增加，但也會趨于一致達到收斂，從而看出該算法具有很好的魯棒性。

2.2 算例1

在Simulink 下搭建圖2 的仿真系統，采用本文所提的分布式優化控制策略，設定微電網t=0 s時孤島模式運行，同時投入優化控制器,得到的仿真結果如圖6 所示。

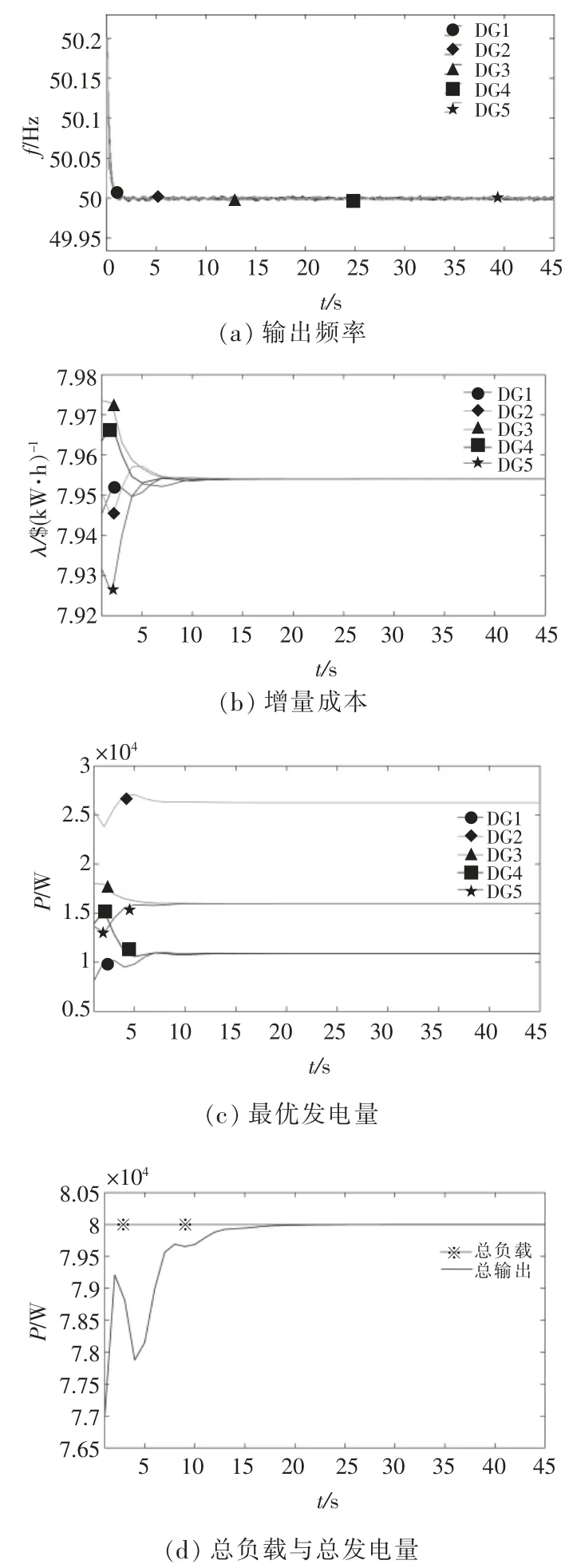
圖6 仿真結果Fig.6 Simulation results

由圖6 可知，在一致性算法優化下，輸出頻率很快達到穩定，并最終穩定在額定值50 Hz。在0～12 s，各增量成本收斂到最優增量成本λ*=60.596 8 元/（kW·h），在 15 s 內達到穩定。 當總負載 PD=80 kW，采用傳統集中式的拉格朗日乘子法解決系統經濟優化，得到的最優增量成本λ*=60.596 8元/（kW·h），對應的最優發電量分別為本文與拉格朗日算法得出的結果相同，證明了該算法的正確性。 總發電量和總負載曲線在穩態時達到了相等，即證實該系統滿足供需平衡約束。 本文所提的基于增量成本一致性的優化下垂控制可以實現微電網的優化運行，實現功率的合理分配以及頻率的穩定。

2.3 算例2

為驗證本文設計的微電網分布式控制策略具備抗干擾能力。 設定微電網t=0 s 時孤島模式運行，同時投入優化控制，結果如圖7 所示。

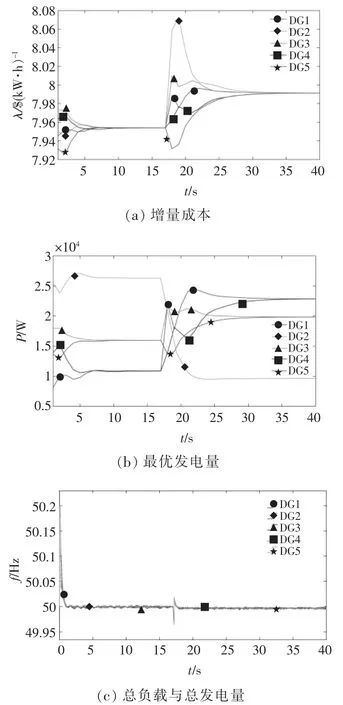
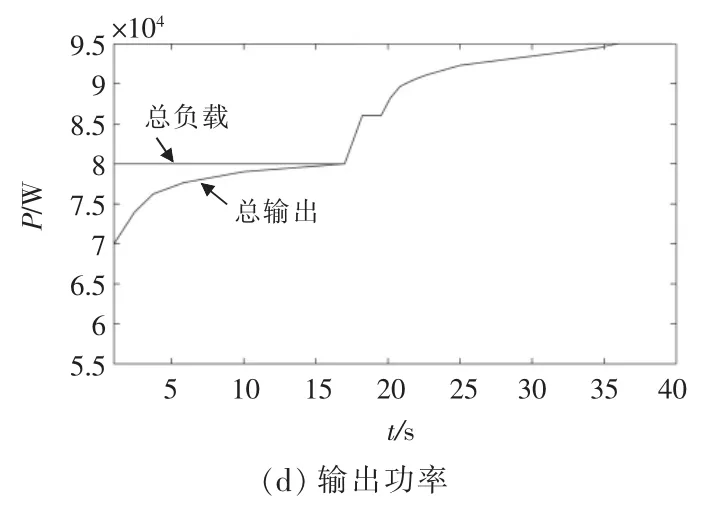
圖7 仿真結果Fig.7 Simulation results

由圖7 可知，在0～17 s，系統達到平衡穩定之后，電力需求從80 kW 突增到95 kW，即ΔP=15 kW。 各節點的增量成本隨著各DG 輸出功率的變化而發生波動，最終在t=33 s，所有發電單元的增量成本都收斂到一致最優值 λ*=60.596 8 元/（kW·h）。從而得出各發電單元的最優發電量證明了該控制系統可以實現微電網的經濟最優化運行且滿足供需平衡約束。在t=17 s 時頻率開始波動下降，在優化控制器的作用下，經過短暫的緩沖，頻率慢慢趨于穩定，最后穩定在額定值50 Hz，從而可以證明該分布式控制具有一定的抗干擾性。

3 結論

針對微電網經濟運行成本及其控制中存在的問題，本文提出了一種基于增量成本一致性的孤島微電網分布式下垂控制策略。 該策略采用兩層的控制模型，基于上層通信網絡的一致性解優化第二層的下垂控制，實現功率的合理分配及頻率值的穩定，達到經濟優化運行的目的，使運行成本最小化。 利用仿真對算法的收斂性以及魯棒性進行了證明，通信網絡無需強連通，各DG 僅通過稀疏通信，就可以達到穩定收斂的效果，減少了控制系統對通信網絡的依賴性。 通過對該控制策略進行仿真，證明了該方法可以實現各發電單元的優化運行，且保證了微電網的頻率穩定在額定值，仿真案例進一步證明了該策略的有效性。