潮流作用下絞吸挖泥船水上管線分布與系纜力分析

朱平，郝宇馳，袁超哲，陶潤禮，孫慧

（中交疏浚技術裝備國家工程研究中心有限公司，上海 201208）

0 引言

水上管線是絞吸挖泥船的關鍵組成部分，在強潮流作用下，水上管線會出現較大的彎曲角度（見圖1），甚至會發生走錨、拗斷等現象，嚴重影響設備安全性和施工效率。

圖1 強潮流作用下的水上管線分布Fig.1 Distribution of floating pipeline under strong tide

對于水體與結構物之間的相互作用以及系纜力研究，目前主要采用計算流體力學（CFD）數值模擬方法。鄒志利等[1]運用數值模擬方法分析了風浪流作用下系泊船的運動和系纜力。肖越[2]、張繼明等[3]研究了錨泊浮體的運動及其系纜力。張婷等[4]基于計算流體力學軟件研究了海洋平臺的波浪荷載。秦崇仁等[5]利用數值模擬方法研究了水上排泥管的系纜力。目前的研究尚未對實際工程尺度下的水上管線分布及其系纜力的計算開展研究。

本文以廈門新機場造地工程為例，對水上管線在潮流作用下的分布及系纜力進行計算研究。

1 數值模型控制方程

在本文中，考慮流體為不可壓縮的黏性流體，以Navier-Stokes方程作為控制方程，VOF方法追蹤自由表面，建立三維數值模型，模擬水上管線與水流相互作用的過程，并計算水上排泥管的系纜力。在數值模型中，系泊纜繩近似為圓柱體結構，纜繩結構的受力分析（見圖2）方程如下：

式中：mp為系泊纜繩的質量；vp為纜繩運動速度；G為纜繩重力；B為浮力；T1和T2為纜繩兩端拉力；Dn和Dt為纜繩在法向和切向受到的拖曳力；CD，n和CD，t分別為纜繩法向和切向的拖曳系數；ρ為水的密度；An和At分別為纜繩法向和切向的截面積，vr為纜繩相對于水流的速度；vr，n和 vr，t分別為 vr在法向和切向的速度分量。

2 模型驗證

為了保證數值模型對水上管線系纜力計算方面的可靠性，利用水上管線物理模型實驗結果[5]，本文對數值模型進行驗證。按照物理模型實驗條件對數值模型進行相應的設置，其中，排泥管長度為0.33 m，外徑0.083 m，邊界流速0.42 m/s，波高與波周期分別為0.042 m和1.3 s。數值模型計算得到的系纜力結果與物理模型試驗結果對比如圖3所示。數值模型的系纜力計算結果與物理實驗結果比較吻合，最大系纜力數模計算值為0.33 N，與物理模型實驗值0.31 N基本一致，表明該數值模型能適用于水上管線的系纜力計算。

圖2 纜繩受力分析Fig.2 Force analysis of cable

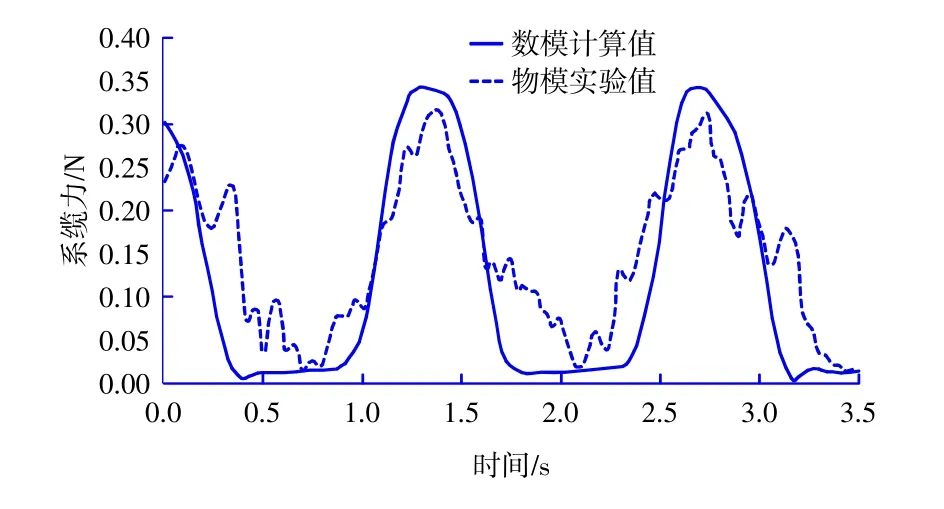
圖3 系纜力數模計算值與物模實驗值的對比Fig.3 Comparison between simulated mooring forces and experimented mooring forces

3 數值模擬試驗

3.1 數值模型設定

在廈門機場造地工程中，水上管線采用外徑為0.88 m，長度為12 m的浮片式鋼質排泥管，并通過2 m的橡膠管進行兩兩相互連接（見圖4）。水上管線長度一般為500 m左右，每隔80～100 m設置1個錨進行固定。

圖4 水上管線連接示意圖（mm）Fig.4 Connection diagram of floating pipelines(mm)

三維建模計算模型（見圖5）主要由排泥管和錨鏈組成，每根排泥管模型的參數與實際工程中的排泥管參數一致，拋錨間隔設為固定值90 m。模擬管線總長度設為210 m，計算域長度為60 m，寬度為240 m，高度為11 m，水深則為8 m，網格精度為0.6 m。為了較為準確地刻畫出排泥管真實形狀，在排泥管運動的區域進行網格加密，網格精度為0.15 m，計算域總網格數約為320萬。對于邊界條件的設定，上游設置為流速邊界，下游為壓力邊界，兩側為對稱邊界，底部為壁面邊界，上表面為大氣壓強邊界。

圖5 水上管線三維模型示意圖Fig.5 Three-dimensional model of floating pipeline

以往的研究[6]表明，廈門附近海域的潮流最大流速能達到2.0 m/s，絞吸船極限作業流速亦為2.0 m/s。為了研究水上管線在不同潮流流速下的分布及其系纜力，本文設置了4組數值試驗（見表1），分別為試驗1（常規工況A，邊界流速為0.5 m/s）、試驗2（常規工況B，邊界流速為1.0 m/s）、試驗3（常規工況C，邊界流速為1.5 m/s）和試驗4（極端工況A，強潮流作用，邊界流速為2.0 m/s），比較分析4種不同工況下水上管線的分布和系纜力大小。表1中，試驗5與試驗6為極端工況下不同錨固間隔的系纜力分析試驗。

表1 試驗工況及其最大系纜力Table 1 Test experiments and the maximum mooring forces

3.2 數值模擬結果分析

3.2.1 水上管線分布

由模擬結果可知，在常規工況下，當潮流流速為0.5 m/s時，水上管線呈現弧形分布，彎曲角度較小，約為10°（圖6（a）），水體對于水上排泥管的作用力比較小；當潮流流速為1.0 m/s時，水上浮管的最大彎曲角度達到20°左右（圖6（b））；當潮流流速達到1.5 m/s時，部分排泥管頂部已處于水面以下，水上浮管的彎曲度進一步加大，約為 25°（圖 6（c））。

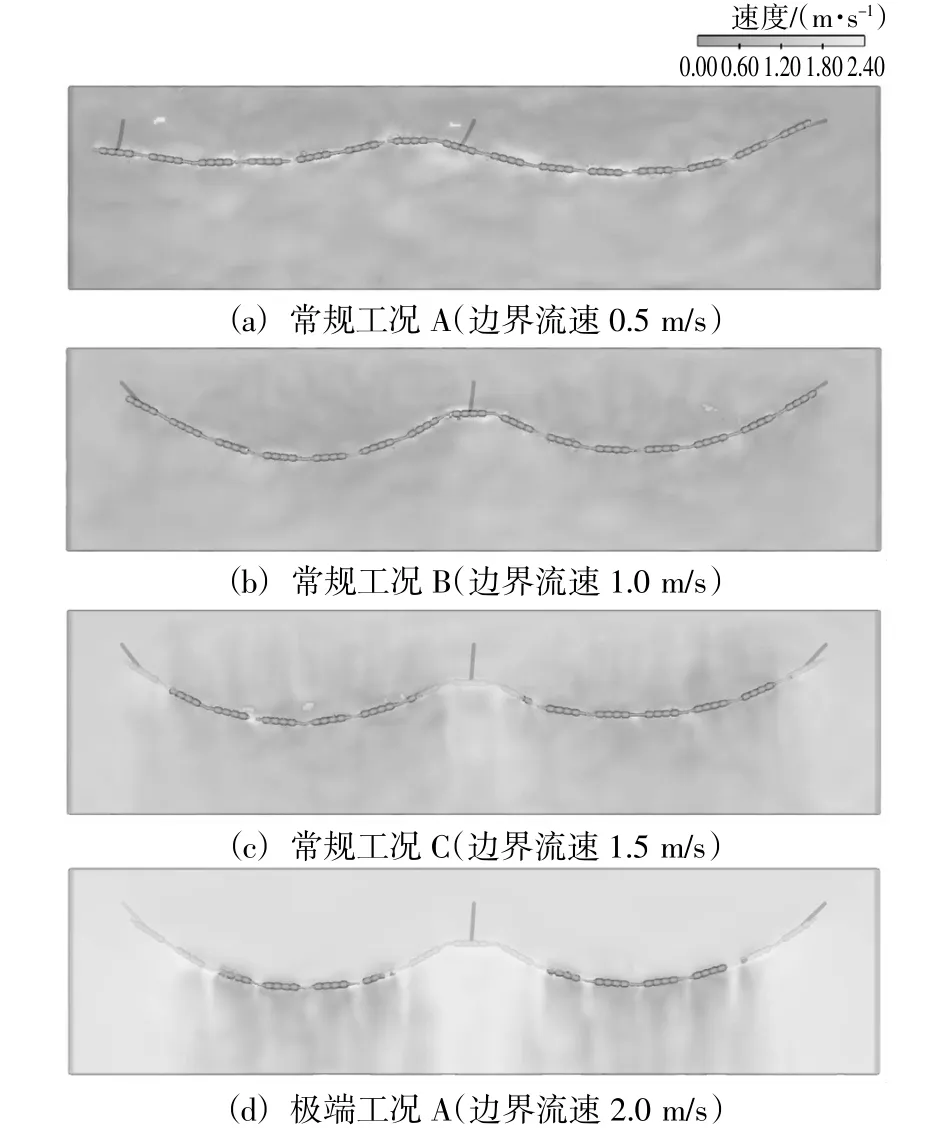
圖6 不同工況下的水上管線分布Fig.6 Distributions of floating pipelines under different conditions

由圖6（d）可知，在強潮流工況下，部分排泥管整體浸入水中，表層水體直接從排泥管頂部流過，這與實際強潮流作用下的排泥管分布狀態較為一致（見圖1），水上管線彎曲非常明顯，彎曲角度達到了30°左右。此種狀態下，管道內的壓力損失較大，應將水上管線盡量保持順直，減小水流對排泥管的沖擊力，從而減小水上管線彎曲度和壓力損失，提高管道內泥漿的輸送效率。

3.2.2 系纜力結果

廈門新機場工程附近海域的底質以細粉砂和細砂為主[7]，工程中用于固定水上管線的海軍錨在該種土質下的最大錨抓力約為350 kN[8]。由表1可知，在常規工況條件下，當潮流流速為0.5 m/s或1.0 m/s時，最大系纜力遠小于最大錨抓力；當潮流流速達到1.5 m/s時，最大系纜力達到360 kN左右，超過了最大錨抓力。因此，在常規工況下，當流速小于1.0 m/s時，當前的固定錨設置完全能保證施工的正常進行；當流速達到1.5 m/s左右時，常規90 m的錨固間隔可能會產生走錨的現象，對水上浮管的安全和施工效率產生影響。

在極端工況下，潮流流速達到2.0 m/s，在錨固間隔為90 m的狀況下，水上管線的最大系纜力達到了529 kN（見表1），該值已經超過了最大錨抓力（350 kN）。若仍然以常規90 m錨固間隔對水上管線進行拋錨固定，容易發生走錨的現象，從而對水上管線設施造成破壞以及降低生產效率。

將上述4種90 m常規錨固間隔的工況下潮流流速與系纜力結果進行綜合分析后可知，當潮流流速＜1.4 m/s時，水上管線的最大系纜力在海軍錨可承受的受力范圍之內，常規的錨固設置能確保水上浮管的穩定性和正常施工的開展。當流速≥1.4 m/s時，排泥管的系纜力超過350 kN，拋錨間隔為90 m的常規錨固設置已經不足以確保水上管線的安全與穩定，可能會發生走錨等現象，需要增加拋錨數量或減小錨固間隔等安全措施來保證水上管線的穩定性。

為了確定強潮流作用下合適的拋錨數量和拋錨間隔，本文在試驗4的基礎上進行了不同錨固間隔的試驗5和試驗6（見表1，邊界條件與試驗4相同，拋錨數量設為4和5，相應的拋錨間隔分別為60 m和45 m）。當拋錨間隔設為60 m（拋錨數量為4）時，在極端工況條件下，排泥管的最大系纜力達到了445 kN（見表1），超過了海軍錨的最大錨抓力。當拋錨間隔調整為45 m（拋錨數量為5）時，水上管線的系纜力在336 kN，小于最大錨抓力。因此，在極端工況下，為了能保證施工的正常開展，建議將常規的錨固間隔減小至40～50 m，使得排泥管的系纜力在最大錨抓力范圍內，才能確保水上管線的穩定和施工的正常開展。

4 結語

本文采用CFD數值模擬的方法，從實際工程尺度分析了潮流作用下的水上管線分布及其系纜力變化。主要結論如下：

1）水上浮管在常規的80～100 m錨固間隔條件下，當潮流流速＜1.4 m/s時，排泥管受水流作用的最大系纜力小于錨抓力，潮流對施工效率不會產生影響；當潮流流速≥1.4 m/s時，水上管線的系纜力超過了最大錨抓力，需要減小錨固間隔來確保水上管線的安全與穩定。

2）在強潮流作用下，流速達到2.0 m/s時，水上管線彎曲非常明顯，常規的80～100 m錨固間隔下的最大系纜力遠遠超過了最大錨抓力，會導致走錨現象的發生，建議將錨固間隔減小至40～50 m，確保施工的正常開展。

本文對水上管線的設置及其外部影響因素進行了一些簡化，外部環境作用僅考慮潮流的影響。實際工程中水動力環境更為復雜，所以對水上管線分布和系纜力分析還需要進一步的深入研究。