用MATLAB進行棒材生產線車間分段剪至冷床距離的優化計算

周立騫

（中冶京誠工程技術有限公司，北京 100176）

影響棒材連軋車間總長度的主要因素之一是分段剪到冷床入口的距離。軋件經分段剪切成倍尺后，先加速，與后一根軋件脫離，然后勻速運動一段距離，最后制動停止，進入冷床（圖1）[1]。生產實踐證明：如果分段剪與冷床入口距離過短，則前后倍尺鋼無法拉開足夠的距離，導致軋件進入冷床容易產生亂鋼情況，耽誤正常生產；過長，則會使車間長度增加、廠房面積增大，導致投資相應增加。因此，為了保證棒材生產的正常進行，減少投資費用，需要科學合理的計算這一距離。

圖1 軋件速度變化示意圖

1 優化條件

（1）某棒材車間生產線最大終軋速度v0=18m/s，加速后最大速度v1（1.05v0～1.10v0），上冷床前速度v2=0m/s，制動裙板最短運動周期2.2s。

（2）制動開始時前后軋件頭尾拉開的距離L=1m。

（3）輥道對鋼的摩擦系數f1=0.3，制動裙板對鋼的摩擦系數和過渡板對鋼的摩擦系數f2=0.35。

（4）輥道與水平面的夾角α=12°，制動裙板斜面與水平面的夾角β=35°。

圖2 上冷床裝置結構

（5）軋件上冷床的過程[2]。

①軋件經倍尺剪切之后，在輥道上加速，與第2根倍尺鋼脫離，進入冷床入口輥道（傾斜輥道），此時裙板在高位；②當裙板下降到低位時，第1根倍尺鋼滑下，落到裙板頂面與過渡板側面形成的夾角處，開始摩擦制動；③裙板立刻返回到中位，使第2根倍尺鋼仍沿傾斜輥道運行，第1根倍尺鋼完成摩擦制動；④裙板上升到高位，第1根倍尺鋼滑落到冷床矯直板第1個齒槽中，然后在向冷床出口一步一步輸送的過程中空氣自然冷卻；⑤裙板下降到低位，第2根倍尺鋼滑下，開始下一工作周期。

2 建立模型[2]

2.1 加速段加速度a1的確定

鋼材在加速輥道上的狀態及受力情況。

圖3 鋼材在加速輥道上的狀態及受力情況

由圖可得：

N2cosα=N1sinα

N2sinα+N1cosα=mg

解此聯立方程組，得：

N1=mgcosα

N2=mgsinα

式中：N1—輥道對軋件的支持力；

N2—裙板對軋件的支持力；

m—軋件質量；

g—重力加速度，取10m/s2。

由摩擦定律及牛頓第二定律可得

ma1=N1f1-N2f2=mgf1cosα-mgf2sinα

a1=g(f1cosα-f2sinα)

2.2 減速制動段加速度a2的確定

鋼材在減速段即在制動裙板上的狀態及受力情況。

圖4 鋼材在制動裙板上的狀態及受力情況

由圖可得：

N3sinβ=N4cosα

N3cosβ+N4sinα=mg

解此聯立方程組，得：

N3=mg[cosα/cos（β-α）]

N4=mg[sinβ/cos（β-α）]

由摩擦定律及牛頓第二定律可得：

ma2=f2（N3+N4）=mgf2[（cosα+sinβ）/cos（β-α）]

a2=gf2[（cosα+sinβ）/cos（β-α）]

2.3 距離優化

設S為軋件加速、勻速到最后制動所走過的總路程，S1，S2，S3分別為加速、勻速、制動階段軋件所走過的路程，則：

S=S1+S2+S3

S1=v0t1+a1t12/2

S2=v1t2=（v0+a1t1）t2

S3=v1t3-a2t3

2/2=（v0+a1t1）t3-a2t3

2/2

根據工藝要求.前后兩軋件在制動開始時，頭尾應拉開距離L(m)，可得關系式：

L=S1+S2-v0（t1+t2）

L=v0t1+a1t12/2+（v0+a1t1）t2-v0（t1+t2）

則t2=（2L-a1t12）/2a1t1

因v1=a2t3，所以t3=v1/a2=（v0+a1t1）/a2

將t2、t3代入S并整理，得：

t=t1+t2+t3≥2.2

將t2、t3代入t并整理，得：

-a1（a1/a2+0.5）t12-a1（v0/a2-2.2）t1-L≤0

將數值代入計算，得：

a1=2.21m/s2，a2=5.90m/s2

建立模型（用x替換t1）：

minS=0.414x2+15.742x+8.145/x+28.458

s.t. -1.93375x2-1.88071x-1≤0

x≥0

3 MATLAB計算

（1）m文件：非線性不等式約束（圖5）。

（2）非線性目標函數運算（圖6）。

（3）運算結果：t1=0.706s；S=51.315m。

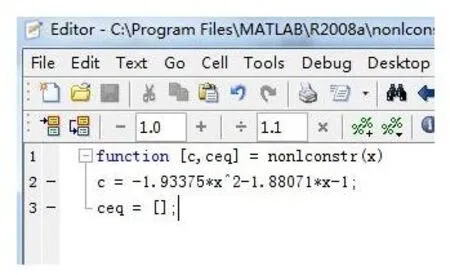
圖5 將目標函數模型設置為非線性不等式約束

圖6 目標函數計算

4 結果分析

優化后的距離為51.315m，此距離是在最高軋制速度18m/s的條件下得出，因此滿足各種規格棒材的生產。

加速段時間為0.706s，加速后的速度v1=19.56m/s，比初速提高8.7%。按照生產經驗，加速后，速度需提升5%～10%。本次優化計算得到了最優加速量，從而計算出最優距離。不會因距離過短，在進入冷床時產生亂鋼；也不會因距離過長而增加占地和投資。