一種改進的有霧圖像去霧算法

何 濤, 謝有慶, 李一航, 徐 昊, 劉甲甲, 余 萍

(1.深圳南山供電局，深圳 518000；2. 深圳供電規劃設計院有限公司，深圳 518000；3.華北電力大學電子與通信工程系,保定 071003)

在電力建設工程中，基于可視化技術的工程管控系統的應用可大大提高工程管理水平，在全天候條件下采集清晰的現場圖像是系統應用的重要保障。近年來由于霧霾天氣的影響，導致圖像采集設備采集的圖像，對比度下降、飽和度降低和色彩失真，對航空拍攝，駕駛輔助和可視化工程管控等應用帶來不利影響。因此，研究如何從有霧的圖像中恢復出清晰的圖像是當前圖像處理領域的重點內容。

早期的圖像除霧方法中，Narasimhan等[1]提出一種基于物理散射的去霧模型，通過這個模型從兩幅或多幅有霧圖像中恢復場景構信息。Kopf等[2]提出通過使用三維地理模型可直接獲取有霧圖像的景深信息來對圖像行去霧。然而，在實踐中獲得這樣的輔助信息可能非常困難甚至是不可能的。因此，這種通過獲取輔助信息的圖像去霧方法在實際的應用中相當有限。

相比早期的圖像除霧方法，近年來國內外研究者又取得了一些重大進展。如Cai等[3]提出的基于神經網絡的深層架構的DehazeNet圖像去霧網絡，在特定的數據集上取得了較好的去霧效果，但需要提供大量的有霧和對應的無霧圖像進行訓練，樣本采集困難，缺乏理論依據。Ren等[4]使用卷積神經網絡，計算每個像素的多尺度特征，并針對不同的去霧問題定制訓練數據，但在真實世界的戶外圖像進行測試時，表現不理想。Fattal等[5]在大氣光與物體表面色度統計不相關假設的前提下，將霧霾圖像分解成恒定區域和透射區域，該算法依賴數據的統計特性，但由于霧霾圖像的顏色信息較少，導致獲取的統計信息不可靠。Tarel等[6]通過對有霧圖像用中值濾波器進行濾波，直接將濾波輸出作為圖像的霧氣面紗值，但中值濾波器不具有保留邊緣信息和細節信息的特性，造成霧氣面紗過度提取而導致去霧后的圖像局部區域色彩失真。He等[7]通過對大量戶外圖像進行統計研究發現大多數無霧霾圖像局部區域通常包含一些低強度像素提出了暗通道先驗的理論。該理論結合軟摳圖算法，可以實現非常好的去霧效果。但復原后的圖像整體偏暗，去霧過程中耗費計算機資源而且在包含天空區域的有霧圖像中會出現暈圈偽影現象。

針對上述問題，通過對大氣散射強度退化模型進行研究，提出一種基于灰色關聯度的引導濾波圖像去霧算法。該算法與傳統算法的不同之處在于，將有霧圖像的像素分為正常像素和被霧霾顆粒破壞的像素，通過計算灰色關聯度判斷出被霧霾顆粒破壞的像素值；然后，通過引導濾波的方法對霧霾顆粒破壞的像素進行分離，在對數域中計算霧氣面紗估計值；按照大氣散射退化模型反演復原出清晰的圖像。最后通過主觀和客觀的評價方式驗證本文算法的有效性。

1 基本原理

1.1 圖像退化模型

在計算機視覺和計算機圖形領域，大氣散射模型被廣泛應用描述霧霾的成像過程[1]，模型公式為

I(x)=J(x)t(x)+A[1-t(x)]

(1)

式(1)中：I(x)為含有霧霾的圖像；J(x)為去霧后恢復出的清晰圖像；t(x)是透射率；A是全局大氣光系數；x是像素點坐標。恢復一幅有霧圖像的目標就是已知I(x)的條件下，通過估計A和t(x)的值，從而由式(1)反演推算出清晰圖像J(x)。在式(1)表示的模型中，透射率t(x)可表示為

t(x)=e-βd(x)

(2)

式(2)中：β表示大氣散射系數;d(x)表示場景深度。由式(2)可知，透射率t(x)是由場景深度和大氣散射系數決定的，通過估計深度圖d(x)和大氣散射系數β來求解透射率。在此基礎上，Tarel[6]引入大氣面紗V(x)：

V(x)=A[1-t(x)]

(3)

由式(3)可以將式(1)式改寫為

(4)

式(4)中:I(x),和J(x)分別是白平衡后有霧圖像和無霧圖像;V(x)是大氣面紗函數;A是全局大氣光系數。

1.2 引導濾波

導向濾波的思想是由He等[8]最先提出的，能夠有效地突出圖像細節，其關鍵是假設引導圖像I和濾波器輸出圖像q之間具有局部線性關系。即假設在以像素點k為中心的窗口wk中，輸出圖像q是引導圖像I的線性變換,即

qi=akIi+bk, ?i∈wk

(5)

式(5)中：(ak,bk)是在濾波窗口wk中假定為常數的一些線性系數。

2 灰色關聯度引導濾波圖像去霧算法

2.1 圖像灰色關聯分析

灰色關聯分析是用序列的相似性來度量序列之間的關聯性[9]。在圖像處理中，經常會對圖像的3×3鄰域的九像素進行相關性分析。即取鄰域窗口中心點的像素灰度值作為參考序列，中心點周圍的8像素作為比較序列，這時參考序列與比較序列中均只有一個元素，具體計算過程如下。

(1)假設系統參考序列為X0=[x0(1)],比較序列為

X1=[x1(1)],X2=[x2(1)],…,X8=[x1(1)]。

γ[x0(1),xi(1)]=

i=1,2,…,8

(6)

式(6)中:ξ∈(0,1)為分辨系數，一般取0.5。

2.2 基于灰色關聯度的引導濾波

假設有霧圖片的像素分為兩種類型，一種是正常的像素點，另一種是被霧霾污染的像素點。通過計算灰色關聯度對正常像素點和被霧霾污染像素點進行判斷，然后對霧霾污染的像素點進行導向濾波，正常的像素點保持不變。以f(i,j)為中心像素的3×3濾波窗口內，對灰色關聯度進行改進，選擇濾波窗口中像素值的均值作為參考序列X0。

X0={x0(1),x0(2),…,x0(9)}=

{c,c,c,c,c,c,c,c,c}

(7)

式(7)中：c=mean{f(i-1,j-1),f(i-1,j),f(i-1,j+1),f(i,j-1),f(i,j),f(i,j+1),f(i+1,j-1),f(i+1,j),f(i+1,j+1)}為濾波窗口中9個像素的均值。濾波窗口內9個像素值作為比較序列X1,即

X1={x1(1),x1(2),…,x1(9)}=

{f(i-1,j-1),f(i-1,j),f(i-1,j+1),

f(i,j-1),f(i,j),f(i,j+1),f(i+1,j-1),

f(i+1,j),f(i+1,j+1)}

(8)

然后由參考序列和比較序列按式(9):

Δ01(k)=|x0(k)-x1(k)|

(9)

計算得到差異信息序列：

Δ01=[Δ01(1),Δ01(2),…,Δ01(n)]

(10)

將差異信息序列代入式(6)計算得到鄰域窗口內像素均值與各像素值的關聯序列γ01=[γ01(1),γ01(1),…,γ01(n)]。最后設定閾值T，如果關聯度序列中的九個關聯度小于設定的閾值T,則濾波窗口內的當前像素判定為被污染的像素點，這時對該像素所在的領域窗口像素進行引導濾波,即假設以f(i,j)為中心像素的Wk濾波窗口內，輸出圖像q和引導圖像I滿足式(5)所示的線性關系。為了求解線性系數(ak,bk)，根據He等[8]的濾波思想可以轉化為使最小化濾波窗口wk中的代價函E(ak,bk)：

(11)

式(11)中：ε為正則化參數。式(11)是一個線性回歸模型，其最優解為

(12)

(13)

2.3 霧氣面紗計算

本文算法與經典去霧算法提取霧氣面紗的方法不同，通過取對數的方法縮小原始圖像和濾波以后圖像像素值之間的差異，以減少大氣面紗中包含的原始圖像的紋理信息和細節信息。然后在對數域中，用原始圖像減去灰色關聯引導濾波后的圖像，將二者的差值取反對數作為原始有霧圖像的霧氣面紗估計值V(x)。然后由式(3)反推出透射率t(x)，從而對原始圖像進行恢復。

2.4 霧靄圖像復原

由大氣散射退化模型表達式可知，要想在I(x)已知的條件下恢復出清晰的圖像J(x)，必須準確估計出透射率t(x)和大氣面紗V(x)。所以只需估計出大氣面紗V(x)的值，就能從有霧圖像中恢復出清晰圖像J(x)。本文中的大氣面紗V(x)表示為

V(x)=exp{aln[I(x)+1]-ln[H(x)+1]}

(14)

式(14)中：a是取值區間為(0,1)的常數；I(x)為原始有霧圖像；H(x)為灰色關聯引導濾波以后的圖像。式(14)中I(x)加1再取對數，是為了防止歸一化像素值為零時取對數后的值趨于無窮大，由式(4)可得本文去霧復原的圖像J(x)：

(15)

式(15)中：x表示圖像上點的位置坐標；t(x)是透射率，由式(3)確定；A是全局大氣光系數，其取值采用He等[8]從暗通道中按亮度的大小取0.1%的像素，然后再取這些像素對應在原圖中的最大值作為A。即

A=max{max[Idark(x),0.1]}

(16)

式(16)中：Idark(x,y)表示圖像的暗通道。為了防止t(x)為零，設置一個下限值t0(t0一般取0.1)，即用max[t(x),t0]代替t(x)。

綜上所述，本文算法步驟如下。

假設輸入有霧圖像為I(x)，去霧增強后的輸出圖像為J(x)。

步驟1對原始圖像進行灰色關聯引導濾波,濾波后的圖像用H(x)表示。

步驟2在對數域中，用原始圖像減去灰色關聯引導濾波后的圖像，得到對數域中的霧氣面紗估計值V′(x):

V′(x)=alg[I(x)+1]-lg[H(x)+1]

(17)

式(17)中:a為取值區間為(0,1)的常數,取0.03。

步驟3對V′(x)取反對數，得到霧氣面紗值V(x)：

V(x,y)=exp[V′(x,y)]

(18)

步驟4將V(x)代入式(4)即可得到輸出圖像J(x)為

max{max[Idark(x),0.1]}

(19)

3 實驗與結果分析

為了對本文算法的去霧效果進行驗證，選擇去霧算法研究中常用的有霧圖像進行測試，并與算法DehazeNet[3]、多尺度卷積神經網絡(multi-scale convolutional neural networks,MSCNN)[4]進行比較。本實驗環境：CPU為英特爾 Pentium(奔騰) G4600 @ 3.60 GHz雙核，內存為8 GB，操作系統為Windows10的筆記本電腦，使用 MATLAB 2015b進行實驗。實驗中算法各參數取值為: 灰度關聯閾值T通過多次試驗取0.65，引導濾波器窗口半徑r取4，正則化參數取值為0.01，用原始圖像作為引導濾波器的導向圖。

3.1 主觀評價

實驗采用包含遠景和近景兩種類型的圖片，不同算法的實驗結果，如圖1～圖4所示。

圖1 建筑及周邊近景

圖2 山體遠景

圖3 城市交通遠景

圖4 城市交通近景

由圖1可知，對比的三種算法中MSCNN的去霧效果最好但顏色過于飽和，DeHazeNet去霧后留有部分殘霧，本文算法去霧后的圖像顏色相比于原始霧圖有些許偏離，但卻能反映出更多精細的圖像細節。圖2為同時包含遠景和近景的測試圖片，從遠景(紅色框中云彩的部分)來看所對比的三種算法去霧效果相當，但從近景(紅色框山角的部分)對比可知DeHazeNet和MSCNN去霧后的圖像中山角的部分可視性降低，相對而言我們的算法去霧后的圖像在可視性效果更好。圖3為包含較多活動場景的交通圖像，由圖3可知對于遠處濃霧部分，三種算法去霧效果都不是很明顯，但從整體顏色方面考慮，本文算法去霧效果最佳。圖4為包含霧霾的測試圖片，由圖4可知在濃霧條件下，三種算法的去霧效果都不是很理想，但在同等水平下，我們的算法體現出的人物細節更清晰。

3.2 客觀評價

為進一步對算法的去霧效果進行驗證，采用常用圖像質量評價指標信息熵[10]、平均梯度[11]、結構相似性[12](structural similarity index，SSIM)及峰值信噪比[13](peak signal to noise ratio, PSNR)對不同算法進行比較。圖像的信息熵反映圖像所包含信息量的大小，信息熵越大則圖像包含的信息量越大;平均梯度反映圖像對微小細節反差表達的能力，用于評價圖像的模糊程度。平均梯度越大，表示圖像紋理層次信息越多，圖像越清晰；結構相似性(SSIM)是一種衡量兩幅圖像相似度的指標，從圖像組成的角度反映場景中物體結構的屬性；SSIM越大表明算法對原始圖像的結構信息完整性的保留能力越強，對有霧改善效果越明顯。

表1比較了圖1～圖4所示去霧算法結果對應的客觀性能評價指標，由表1可知有霧圖像經本文算法處理后的性能指標大部分大于DehazeNet和MSCNN算法。由此可知，在包含某些常見場景的有霧圖像中，本文算法在反映圖像細節信息和可視性等方面具有一定的優勢。

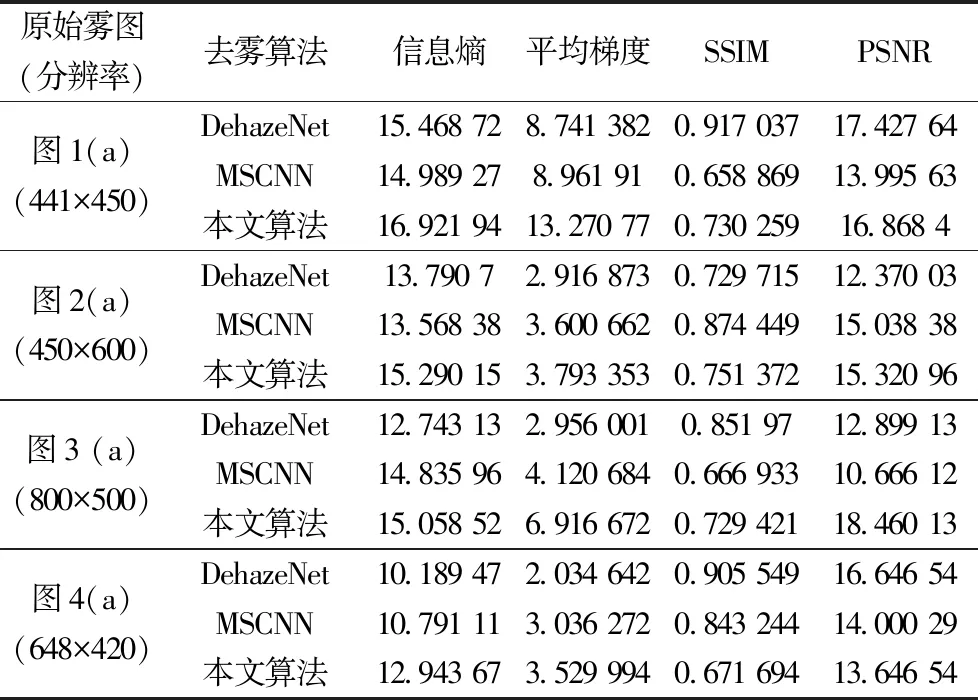
表1 算法去霧客觀性能比較

3.3 目標檢測試驗

在可視化技術的工程管控系統應用中，經常將去霧后的圖片用于目標檢測。實驗使用YOLOv3作為檢測網絡，三種去霧算法去霧后的圖片作為輸入進行目標檢測，可視化結果和檢測的量化結果分別如圖5、圖6和表2所示。

圖5 較少目標圖像去霧后YOLOv3檢測對比

圖6 較多目標圖像去霧后YOLOv3檢測對比

表2 圖像去霧后使用YOLOv3檢測的結果

由表2可知，將含有多種目標的有霧圖像使用上述三種去霧算法進行處理后再檢測，本文算法檢測出的目標個數最多，耗時最少且圖像包含的目標越多去霧后檢測的效果越好，具有一定的工程應用價值。

4 結論

將灰色關聯理論應用于圖像去霧中，采用取對數的方法計算霧氣面紗，細化了霧氣面紗的估計值，按照大氣散射退化模型反演恢復出去霧后清晰的圖像。在提升視覺效果的同時，有效地保持了圖像邊緣細節信息，最后通過主觀和客觀評價的方式驗證了算法的有效性。本文算法也有不足之處，主要體現在采用灰色關聯度對像素進行濾波判斷時閾值的設定是通過多次實驗采用的一個相對較好的值，不能保證其是最佳閾值。未來努力的方向是研究一種能夠進行自適應閾值設置的算法，以取得更好的去霧效果。